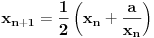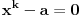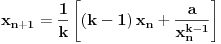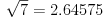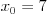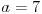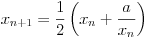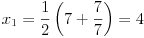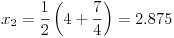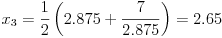Evo probacu da objasnim. Nadam se da necu da napravim veliku zbrku ko sto umem.

Elem, algoritam. recimo da nam je dat broj 196.1 iz koga treba izvaditi kvadratni koren.

Pocev od decimalne tacke ulevo i udesno, broj se podeli na grupe od po dve cifre. Dakle: (podelu sam oznacio zapetama)

1,96.10,00,00,...

(grupe po dve nule ne moraju da se pisu, videce se kasnije)

Prva, "najlevlja" grupa (u kojoj je samo cifra 1) se obradjuje na sledeci nacin: Treba odgovoriti na pitanje koja je najveca cifra koja dignuta na kvadrat daje broj manji ili jednak najlevljoj grupi? U ovom slucaju odgovor je 1 i to je prva cifra rezultata. Potpisuje se ovako:



pri cemu je ona donja jedinica nastala od 1*1

Potpisana cifra se oduzme od prve grupe, rezultat napise ispod i dopise sledeca grupa:



ovde je dvojka dobijena kao 2 * (ono sto za sada stoji u rezultatu). x se odredjuje iz pitanja: koja je najveca cifra takva da kada se stavi na mesto x i dobijeni brojevi (2x i x) pomnoze, daje broj manji ili jednak 96. U ovom slucaju (ocigledno namontiranom) odgovor je 4. 4 kalemimo na rezultat, prepisujemo sledecu grupu od dve cifre, stavljamo decimalnu tacku posto smo u 'obradi' broja kog korenujemo stigli do decimalne tacke i potpisujemo dalje:



Ovde je 28 dobijeno kao 2x14. Istim pitanjem kao malopre utvrdjujemo da je jedina cifra x koja ispunjava uslov zapravo nula. Na ovaj nacin moze se dobiti proizvoljan broj cifara. Nadam se da mozes da pokupis ideju i da objasnis.




** E da, sad sam video da code tag unistava vodece razmake (prilicna besmislica!) tako da brojevi nisu lepo potpisani jedan ispod drugog. Nadam se da se ipak vidi sta treba.

hvala na tako detaljnom objasnjenju
nisi napravio zbrku, ovako na prvi pogled izgleda mi jasno ... samo da me ne pita niko zasto :)
salim se

pozdrav

Pronasao sam danas ovo:

http://mathforum.org/dr.math/problems/tim3.30.98.html

gde je sve objasnjeno detaljnije a i lepse je formatirano.

poz.

svaka cast,filmile,na tolikom strpljenju

stvarno svaka cast...

hvala ti jos jednom filmile
cao

Neko je već postavio davno ovo pitanje, ali se ne sećam da je neko odgovorio. Naime, radi se o fazonu koji izračunava (kvadratni) koren bilo kog (pozitivnog) broja. Pogledajte sledeći niz:




I sad nas, na primer, zanima koliki je koren broja 2. Umesto konstante a stavite dvojku i takođe Xo=2. Izračunajte X1, X2, X3, ... (preko rekurentne formule sa početka) i videćete da kako n raste - tako je tačnost sve veća. Međutim, već za n=3 dobija se i više nego dovoljan rezultat.

[Ovu poruku je menjao seven dana 07.10.2002. u 13:09 GMT]

Postoji jos jedan nacin koji sam ja zaboravio...:)Kad pronadjem negde postovacu vam.

http://www.elitesecurity.org/tema/7812#58493

U medjuvremenu sam shvatio i princip koji stoji iza racunanja korena na ovaj nacin. Postalo je ocigledno (ali ne i lako!)
kako se ovako moze sracunati i kubni koren.

poz.

Sve te formule dobijaju se približnim rešavanjem jednačine



Njutnovom metodom tangente.

Opšte rešenje, za svaki ceo broj k, je:



Za početno x može se uzeti bilo koji broj veći od nule.

Ovaj, da li to znači da:



radi?!

f

Ja koristim onaj izlizani fazon za koren koji mi je totalno uspesan. Nadjem brojeve koji se sadrze u broju koji treba korenovati duple pokrati i to je to

144|
2kratimo
72
2
36
2kratimo
18
2
9
3kratimo
3
1

i ostaje nam 2 * 2 * 3 a to je 12 prosto i ne zahteva pamcenje formula ko sto su NAVEDENE

Mozes li Sevene izvaditi detaljno korijen iz 7 po formuli koju si dao. Unaprijed hvala!

Postavimo početne uslove:





A sada primenimo formulu:









I kao što rekoh, u većini slučajeva već za n=3 se dobije sasvim praktično zadovoljavajuće rešenje.
Treba primetiti da se posao svodi na možda nekom dosadno ručno množenje i sabiranje, ali poenta je da se može izgurati. Ovo je posebno bitno ako na ispitu ne možete da koristite digitron, a potrebna je relativno tačna vrednost korena, recimo zbog ucrtavanja vrednosti na grafik itd, itd. ...

Neko je ucio Numericku :)

Postoji i jednostavniji nacin za racunanje korena sa proizvoljnom tacnoscu.
Slican je postupku za deljenje brojeva (koji se uci u ~3 razredu osnovne)

Medjutim ja nisam dobar objasnjavac pa bih molio ako neko zna taj postupak, a bolji je predavac od mene da isti objasni. Ako ne ja cu pokusati kasnije...

U više navrata smo objašnjavali i taj drugi algoritam. Ali na žalost uopšte sad ne mogu da pronađem te poruke.

f

Znam za taj fazon ali kako ces tako naci koren iz npr.147?

A kako se računa koren nekog broja na odredjen broj decimala?

Pa ako ti treba neki razumni broj decimala koristi formulu koju je stavio Caslav, mada moze i neki Taylor-ov razvoj

treba mi sa 35 decimala

ovo za obicni koren sam shvatio,ali za kubni i +1...
da li nelo moze pesacki da to pokaze?
ajde

Pa piše ti formula i za kubni i za sve ostale, poslao je Časlav Ilić. Mrzi me sad da radim pešački, nije nikakva mudrost samo treba računati.

a kako uraditi pjeske korijen iz nekog reanog broja....

A kako se trazi "rucno" koren binoma?

Hahahahaha jbg ja opet ne kontam.Radili smo prosle god iz matisa i sada treba ponoviti za ovu,medjutim ja nemam svesku,pa sam probala ovde.Decko ti si objasnijo sasvim ok i nisi nista zapetljao,ali jbg kada "imam" te vijuge za matematiku hahahah