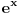Kao prvo, pitanje je vrlo zanimljivo, ali izgleda da i nije tako jednostavno.

Čitajući jednu knjigu („Kurs matematiki: algebra i analiz“ od Š. Pizo, M. Zamanskij) u uvodu (“Soveti čitateljam“) kaže:
„Dlja izučenija matematiki neobhodimo ponimat, čto sostavljaet predmet etoj nauki i kakova ee cel.“
(kako ne znam ruski, prevod bi približno bio: za izučavanje matematike je neophodno znati koji je predmet te nauke i kakva je ona sveukupno)

Međutim, tekst se prostire na nekoliko stranica, a glavna teza je da je matematika „instrument neophodan za druge nauke i svu delatnost inteligentnog čoveka“. Ništa konkretnije od toga ne kaže, mada je izričito istaknuto da je važno znati koji je predmet matematike kao nauke.

Na par mesta sam sreo i (starije, možda starogrčke) definicije da se matematika bavi brojevima i prostorom (misleći na aritmetiku i geometriju), ali čini mi se da moderna matematika nešto drugačija.

Možda je dovoljno reći da je matematika oruđe za rešavanje problema na koje nailaze ljudi, ali meni se čini da je to nekako... mutno!

Zato, ne znajući odgovor, i ja želim nešto više o ovome da utvrdim, i sve u kontekstu moderne matematike kao nauke (ili, šta ja to zapravo studiram ;).

Odgovor je vrlo jednostavan i nemisteriozan - matematika je jedno najobičnije, ali i najneophodnije sredstvo, alat za rešavanje raznoraznih problema.

Odnosno, njena poenta i svrha nije filozofska (bar ja tako vidim, jer od filozofiranja nema vajde), već praktična, dakle nama treba mehanizam (činjenice, zakoni ...) kojim ćemo modelirati neku fizičku pojavu, proces ... i doći do željenog rešenja praktičnog problema, a taj mehanizam je matematika. Sve što se koristi da se dođe do cilja je sredstvo, a matematika je upravo to.

Matematika (grc.) jedna od najstarijih nauka, poznata otkako postoje istorija i pismenost. Nastala je, verovatno, iz svakodnevnih potreba za brojanjem i prebrojavanjem, kao i iz potreba za merenjem i uporedjivanjem prostornih odnosa. Tokom hiljada godina svog razvoja, prerasla je i nadrasla svoje izvore toliko da se, danas, tesko moze dati definicija matematike koja ne bi bila nepotpuna - toliko je siroka oblast ljudske intelektualne delatnosti koju matematika obuhvata. Uz ogradu da je i to, mozda, nedovoljno matematika se moze definisati kao nauka o formalnim odnosima svih vrsta. Ipak na pitanje "Sta je matematika?", najbolji odgovor se dobija izucavanjem same matematike.



Matematika - Fizika
ISBN 86-07-00666-5

Na ovaj način se sve može okarakterisati kao „sredstvo“:
— Fizika je sredstvo za spoznavanje objektivnih odnosa koji važe oko nas i poboljšanje uslova života.
— Psihologija je sredstvo za spoznavanje odnosa u nama samima, i između ljudi (gde je granica između sociologije?)
— Oranje je sredstvo za poboljšanje roda. Traktor je sredstvo za poboljšanje Oranja (i još nečeg drugog).

Prema tome, ovime nismo ništa rekli, pošto je sve u manjoj ili većoj meri sredstvo. Ne postoji nijedan konačni cilj u čovekovoj delatnosti, pa je sve sredstvo, i sve je cilj.

Naravno, gornji navod sredstava nije konačan niti sistematičan: to je samo primer istog obrazca razmišljanja.

Citat koji si izdvojio ide zajedno sa ostatkom gornjeg teksta i tada je potpun i smislen vezano za ovu temu, a onda nijedan od tvojih primera nije dobar ...

Ali lepota matematike je i u izucavanju svega onog sto nema veze sa zivotom :)

Hocu reci, postoji punooooooo teorija koje zive samo sebe radi (mada pre ili kasnije se nadju primene).

Tako da mislim da je prvi korak da pronadjemo sta je oblast delatnosti matematike (brojevi, tacke, skupovi ?).

Ukratko ja matematikom smatram unijom svih teorija za koje postoji formalna teorija koja ih u potpunosti opisuje.

Dakle sta izucava matematika, koje objekte ?

Ako je matematika unija svih teorija, onda možemo još bolje da je opišemo. Recimo, u tu uniju teorija ulazi i teorija iz oblasti matematičke analize, a kao što je poznato, potrebna je samo aksioma supremuma da bi se presekao cirkulus viciozus i da bi se cela analiza izvela apodiktički (što je naravno nepraktično), dakle umesto da u uniju trpamo sve teorije, teoreme, strpamo samo jedan aksiom. I to ponavljamo beskonačno puta, i na kraju ćemo doći do zaključka da u taj skup ulazi samo jedna super aksioma ??? Hmm ... to bi baš bilo zanimljivo, hehe ...

Zapravo, chupcko, ti bi želeo da raspravljamo o metodologiji matematike ?

Matematika nije prirodna nauka ! Zato i postoji prirodno-matematički smer u gimnaziji, a ne samo prirodni, jer u njega ne ulazi matematika. Pa šta je onda ako nije ni prirodna ni društvena nauka ? Nema veze ni sa prirodom ni sa društvom ? KORISTI se i u prirodnim i u društvenim naukama. Ona je način razmišljanja nevezan nizašta konkretno. A opet, postavlja se pitanje, da li bi matematika ovakva kakva je važila i za neku drugu dimenziju ? Da li je invarijantna od sistema ?

Ne možemo da kažemo da matematika izučava objekte (bilo fizičke, bilo apstraktne), jer se ona prožima kroz sve živo i neživo, implementirana je u sve.

Verovatno, konačan odgovor ne postoji, mogu postojati samo različita viđenja koja je lepo čuti ...

Eh lepo je cuti nekada misljenje nekog inzinjera o matematici, svakako da mozemo da pricamo o objektima kojim se bavi matematika.

Mada ja sve vise zastupam tezu da se matematika bavi simbolima :).

Simbolima koji doduse nesto nekada i znace, ali nije pametno oslanjati se na gnoseolosko iskustvo koje nas vezuje za taj simbol.

Secam se price sa jednim masincem kome sam oko 4 sata pricao o neeuklidskim geometrijama i na kraju je covek uzeo papir, dao mi olovku, nacrtao pravu i tacku van nje i rekao : ajde sada kada si pametan, nacrtaj te dve paralelne ako mozes ....

Nego ajde prvo da definisemo teoriju, cisto da ne ispadne da samo neke tamo jadne aksiome ulaze u teorije, gde su tu objekti, gde su tu pravila zakljucivanja (izvodjenja), gde je tu meta matematika?

Zanimlljivo je sto za sve druge nauke moze da se kaze cime se bave, a za matematiku ne moze (ili necemo), dakle ili matematika nije nauka ili je to metanauka :).

Uostalom koja je etimologija reci matematika ?

Matematika je nauka o računu.

Pošto je matematika definitivno najformalizovanija nauka, teško se može naći odgovor na formalan način. Uostalom, pokazano je da formalna teorija, kada se dopusti da govori o sebi, daje nepotpunost.

Svako trezveniji zna da definicije postoje samo u apstrakciji. Ovde mi raspravljamo o tome šta matematika znači za nas. Uostalom šta je nauka? Ili šta je to definicija? (Ako definišemo definiciju, koristili smo istu, pa to malo smrdi). Još su se stari grci mučili na tu temu. I do sada niko nema odgovor. Prosto zato što se on ne može dati na način na koji to naš racionalni deo očekuje.

Npr. definicija je uvođenje novog pojma. Dakle, prirodno se očekuje da svako zna šta je to uvođenje novog pojma, pa je to nepotrebno definisati ;). Ali ako to zna, šta onda ova definicija daje novo? Novo ime za stari pojam? Neku vrstu osvešćivanja intuitivno jasnog pojma? Moderna matematika prećutno podrazumeva da ništa pre teorije ne postoji, pa se ona stvara iz aksioma i pravila zaključivanja. (U tom smislu matematika je vrhunska apstrakcija racionalnog dela ljudskog uma.) Naravno, to ne ide baš tako. Jer kad krenemo unazad do logike pa jezika pa... stići ćemo do primata, a onda do big benga :). Time se samo pravi neophodni rez između intuicije i svesti.

Zato, kada razmišljam o definiciji, zamišljam situaciju u kojoj ono što se definiše ne postoji. A onda u kakvom je odnosu sa onim što, prećutno, postoji. Pri tome se trudim da u postojeće ne uključim definanta. Generalno, to je nemoguće, ali postoji odgovor kojim ću biti zadovoljan. Taj je dat na početku.

U tom smislu, ne bih ovde zahtevao neki formalan odgovor. Neka ljudi jednostavno iznesu svoje mišljenje.

Matematika smo mi.

Matematika je rekao bih delom veština, delom nauka, jer ona generiše svoje modele iz mišljenja, često na osnovu postojećih modela u prirodi, ali nije ograničena na njih.
Za one koji je uče, ona je nauka, a za one koji je proširuju, ona je umetnost.

Ono čime se matematika bavi u odnosu na prirodu (u smislu stvarnost, praksa) jeste apstrakcija i generalizacija, stvaranje novih pojmova koji pojednostavljuju opis složenih pojava (komprimuju bez gubitaka količinu informacija koje imamo o svetu), ali takođe i istraživanje relacija između različitih oblasti unutar same matematike.

@salec:

Je l' si tu definiciju ti izmislio ili si negde nasao? Ako si negde nasao da li mozes da napises izvor jer mislim da definicija nije dobra. Ispadne da su i filozofija, fizika cak i ligvistika podskupovi matematike sto nije tacno.

Ajde napisi izvor definicije.

@darkosos:
Postoje stvari koje se ne definisu. Recimo tacka, prava i ravan. Pretpostavljam da se tako ni definicija ne definise. Mozda se cak ni matematika ne definise. Ne znam.
Nego, je l' mozes i ti da napises izvor definicije koju si stavio u tvoj post?

Srki, sad si me postideo, a samo sam hteo da iznesem svoje misljenje, kako nas je darkosos i pozvao.

Pokusao sam da je izmislim na licu mesta, na osnovu prisecanja svega za sta znam da spada u matematiku, mada ne iskljucujem mogucnost da sam nekad negde procitao nesto slicno. Zao mi je ako sam samo pogresno citirao nekoga. Da li ti znas kako to treba da glasi?

Chupcko je spomenuo simbole, OK, slazem se, samo simboli su oznaka apstraktnih pojmova.

BTW, ako sacekamo dovoljno dugo, neko ce vec ubaciti u matematiku filozofiju fiziku i lingvistiku, ako to vec i nisu ucinili Pitagora, Njutn, Lajbnic, Dekart, Rasel i ostali cijih imena se ne secam. Moram da priznam da nisam matematicar u smislu moje "definicije", nisam sposoban da je prosirim, ali verujem da za neke matematicare sve moze biti matematika. To je jednostavno jedan od izbora nacina na koji sistematizujes cinjenice. Neke cinjenice ipak za sada nemaju svoj matematicki okvir, sto ne znaci da on nece biti stvoren u buducnosti.

U širem smislu, ovo je tačno za svaku modernu „nauku“. Međutim, u užem smislu (kako ti razdvajaš „nauku“ i „veštinu“, „umetnost“) matematika je „najnaučnija“ od svih nama poznatih nauka. Procedure su jasno definisane, i njena upotreba se zaista uči.

Kod većine drugih nauka, ta definisanost nije tako izražena, već uvek postoji „može da bude, a može i da ne bude“ ;-)

Uostalom, na ovu temu je bilo dosta više poruka ovde, ali je ES Proleće 2003 „odnelo“ i te poruke ;-)

Kada sam bio u srednjoj skoli ucili su nas da se ne moze reci da li matematika spada u nauku ili ne. Matematika ima jednu bitnu osobinu nauke a to je tacno razradjen metod. Znaci imamo korake: 1. Hipoteza 2. Teoreme 3. Dokazu uz pomoc tih teorema. Ja sam ove korake otrpilike napisao, mozda nije bas tako ali bitno je da se tacno zna koji je metod matematike. Ali problem je sto se ne zna tacno sta izucava matematika i zbog toga ne spada u nauku.

E sada neko moje razmisljanje.

Mozda je moguce naci odgovor sta izucava matematika ako je podelimo na delove pa vidimo sta ti delovi izucavaju. Postoje 3 dela: aritmetika, geometrija i analiza.
Neke od tih delova mozemo dalje podeliti. Geometrija ukljucuje i trigonometriju a analiza ukljucuje i algebru, analiticku geometriju i numericku analizu.

E sada pokusajte dati odgovore ili nadjite u knjigama definicije ili opise sta izucavaju te oblasti pa cete mozda dobiti odgovor sta izucava matematika.

Za sada je matematika opisana samo kao skup odredjenih metoda. Mada postoji opis kako je matematika odnos izmedju velicina i skup metoda kojima je taj odnos opisan.

@salec
Nema sta da se postidjujes; izneo si svoje misljenje, koje je naravno produkt raznih uticaja kao i sopstvenih sklonosti. Mozda zaista postoji i u nekoj knjizi - tim bolje ;)

@srki
Cini mi se da nisi pazljivo citao moj post. Tacka prava i ravan se ne definisu, jer se precutno podrazumeva intuicija u vezi tih pojmova. Uostalom, ideja o nedefinisanju osnovnih pojmova je skorijeg datuma, a matematika postoji veoma dugo. Definicija nije aksioma, pa bi trebalo da se definise; makar ona matematicka, kao sto postoji definicija teoreme i dokaza...
Moj post je trebao da ukaze upravo na tu igru koju igramo u vezi pojmova u matematici : matematika nije nastala tako sto je neko smislio aksiome a onda 'na slepo' izvodio teoreme! Aksiomatizacija je potreba za postavljanjem logickog okvira, odnosno formalizacijom matematike.
Zato definisanje matematike uzimajuci u obzir samo skorasnje uvodjenje reda mi se ne cini dobrim. Kao bogatas-skorojevic koji zaboravi da je bio siromasan, pa se uobrazi.
Pa cak ni danas ne postoji savrseni red. Imamo intuicioniste, formaliste, konstruktiviste,... koji na razlicite nacine govore o nekim osnovnim postavkama (da li je negacija negacije istina, da li postoji ono sto se ne moze 'konstruisati', itd.). Ili na primer aksioma izbora, koja daje puno ali toliko i trazi; pa aktuelna ili potencijalna beskonacnost...
I na kraju sto se tice mog izvora, on je nesto iznad ramena, povise vrata :). Zar bih predlagao da drugi iznesu svoje misljenje ako sam ja izneo tudje. I ja bih se postideo ;)

srki: a sta cemo sa analitickom geoemtrijom, ili topologijom, a naravno gde spada teroija izracunmljivosti i jos gore, da li je programiranje nekim delom matemtika :)?

Sto se tice definicije definicije, postoji dosta upustava kako treba da izgleda definicija, recimo da je otklonjiva, da je nekreativna ...

Fora je sto sto geometrija ne definise tacku jer su tacke pojmovi na cime se igramo, to jest kaze: posmatramo skup nekih objekata, nazovimo ih tackama ...

Ali u svakom slucaju i dalje postoji potreba za definisanjem matematike, znate ono, dodjete pred odlejenje recimo 5 razreda i kazete: mi cemo izucavati matematiku a matematika je ...

Chupcho, nisi pazljivo citao moj post jer nisi video da sam pomenuo analiticku geometriju. Analiticka geometrija spada u analizu.

A sto se tice prvog razreda, tu se uci aritmetika pa onda je prvacima dovoljno da das i opis (definiciju) aritmetike jer oni ni nece znati za druge stvari niti bi razumeli.

@darkosos

U parvu si, nisam pazljivo citao tvoj post. Zato ni nisam video da si predlozio da svako kaze sta misli pa sam mislio da ste te definicije odnekle izvukli a koliko je meni poznato matematika nije tacno definisana i zato ne spada u nauku jer se ne zna sta tacno proucava nego se zna samo metod koji koristi.

U stvari matematika nije definisana kao nauka tj. nema sve osobine nauke ali zato bi mozda mogla da se definise kao skup metoda koje koriste sve ostale nauke!
To moze da bude i verovatnoca, i izracunavanje integrala ili matematicka logika ako je u pitanju neka nauka kao psihologija itd...

Matematika je umetnost izbegavanja računanja.

pa to mi je nelogicno, sto ne bi to bila algebra, ili mozda logika :)

i dalje me zanima sta bi rekli pred decom a da im objasnimo cime se to bavi matematika.

Pa to „umetnost izbegavanja računa“ može biti i „bežanje sa časova“, „slikanje“, „kuvanje“, „spavanje“, „filo[s|z]ofija“, „sport“, ...

towk, ono sto sam ja rekao moze se posmatrati i sa dozom humora, ali moze i ovako: vecina problema koji se javljaju u matematici (naravno onoj matematici koja se moze primeniti, i koja je 'opipljiva') svodi se na racunanje, a moze se reci da neko zna matematiku ako je u stanju da sa najmanje moguce racunanja resi problem. Mozda jos treba dodati da se matematika razvijala kroz istoriju (i da joj je to vremenom postalo svrha i cilj) u pokusajima pronalazenja sto elegantnijih i preciznijih teorija za resavanje raznih vrsta problema.

da li je matematika isto sto i racun?

Ali i dalje mi nije jasno sta je zajdnicko za sve oblasti matematike koje za sada postoje ?

Da nisu to brojevi (ako jesu sto i fizika nije matematike ?)?

"MATEMATIKA je apstraktna i egzaktna prirodna nauka koja proučava količine i odnose među količinama kao i prostorne forme realnog svijeta po zakonima LOGIKE!" Ovo je najjednostavnija defnicija koja se može naći!

neko ovde rece da "od filozofiranja nema vajde". recimo da sam zbunjen!? sta li su radili svi ti matimaticari koji su bili filozofi?

takodje neko rece da matematika nije prirodna nauka "zato sto se u gimnazijama..." zbunjen sam opet!?
------------------------------
"novi nacini ljudskog rada izazvali su nove probleme, a kad bi ih resili, ljudi su uvek razvijali nove matematicke discipline"
Matematika, Irving Adler

zlatni rez i prirodni brojevi su itekako dokaz da matematika jeste prirodna nauka.

Pa da, lepo je sto svremena na vreme neko da neki odgovor, doduse mene zanima kako ce iko da poveze sve one "objekte" koje izucava matematika a i jednu lepu osobinu da se sve to izuvaca u tri etape:
1. Proucavanje osobina objekata, kao i ekstrakcija nekih vaznijih/lepsih cinejnica i pravila zakljucivanja.
2. Konstruisanje formlane teorije i otudjenje od objekata koje smo posmatrali (bar od onoga kako ih mi prirodno dozivljavamo)
3. Spajanjem tacke 1 i 2 u smislu da "nauke" opisane u 1 i 2 opisuju u stvari iste objekte :).

Naravno ne hvatati se za svaki rec u ovim recenicama, mozda ce neko nekada da ih sredi.

Da li su formalne teorije zajednicko za sve oblasti matematike ? Da li je sve u cemu ima formalnih teorija matematika ? Da li je racunarstvo matematika ili samo jedan obican zanat ?

Recimo da me zanima ovo poslednje, da li je racunarstvo (mada ne u smislu: igram CS, i klikcem po delphiu, ...) nauka i da li se moze podvesti opd neku granu matematike.

To jeste nauka za sebe. Zna se tacno cime se ona bavi. Bavi se racunarima i njihovoj primeni. Zasto bi inace postojali smerovi Computer Science svuda na zapadu...a matematiku mislim da ne stavljaju u nauku jer nema sve osobine nauke. Zna se metod ali se ne zna sta je predmet tih metoda....mada ovo sa formalnim teorijama mi zvuci dobro, osim ako i to nije definisano u matematici...

[Ovu poruku je menjao srki dana 21.08.2003. u 05:02 GMT]

Pa slazem se ja da je nauka i ucenje istorijskih cinjenica napamet, ali se ne slazem sa tim na matematika nije nauka, ja cak ponekad mislim da je matematika jedina nauka :) (bar jedina ima dobru naucnu osnovu).

E sada sto se tice racunarstva, zanimljivo je da ono sto se uci na tim raznim CS (computer science) smerovima nije uvek bas neka nauka vise gomila recepata (kao sto je arapska matematika bila samo spisak recepata kako se nesto radi bez puno nauke oko toga sta se nalazi unutra).

Uostalom ko jos radi dokazivanje korektnosti programa i cita radove o tome :))).

Preciznije me zanima da li je ono sto se izuvaca na nekim CS smerovima stvarno nauka ili samo gomila recepata kako sta i kada uraditi :).

Pa nije istorija samo to. Ipak ima svoj metod kako utvrdjuje istorijske cinjenice i autenticnost dokumenata...Povezana je i sa arheologijom a i sa fizikom (npr merenje starosti pomocu izotopa C-12). Pa onda dugo vremena nisu znali o istoriji Egipta dok nisu uspeli da desifruju heroglife pomocu nekog starogrckog prevoda neke table sa heroglifima, tako da to nije samo bubanje datuma nego jeste nauka.

A inace na CS na zapadu se rade te stvari koje si pominjao a oni uz to imaju i Computer Systems (vise se bave hardverom) a imaju i Software Engineering.

A ja mislim da matematika nije nauka vec je jednostavno disciplina za sebe. Naravno pod tim ne mislim nista lose o matematici vec upravo suprotno. Matematika je nesto posebno. Nju koriste sve ostale nauke. U stvari moglo bi se reci da je matematika jedan od metoda koje koriste ostale nauke sto znaci da je nauka metod.

A zasto ti mislis da je matematika nauka? Kako se ona uklapa u definiciju nauke?

Pa eh, da si kojim slucajem ikada citao fomenka, video bi da istorija je samo slepo slusanje autoriteta :).

Cak sam i ja poceo da verujem da je fomenko u pravu.

Eh, na tom zapadu se bas sve lepo radi, pa opet se svi lome da imaju kojeg naseg elektroizninjera ili fonovca.

Naravno dosli smo do novog pitanja, sta je to nauka :).

Po meni nauka nije samo posmatranje stvarnosti i zapisivanja zanimljivih cinjenica (to jest samo analiza) nego i vestacka sinteza cinjenica i naravno dokazivanje da analizirano i sintetiozvano jedno te isto.

Ali ajde da ipak definisenmo sta je to nauka uopste i da li ej matematika nauka ili ensto iznad ili nesto ispod :).

Pa to se radi na Matematičkom fakultetu u 1. godini studija iz predmeta „Osnovi programiranja“ :-)

Naravno, ne kod svih profesora, i ne baš detaljno, ali C. A. R. Hoara su morali da znaju svi ;-)


Mislim da u uvodu knjige „A=B“, koji je napisao DEK (samo uvod, ne i celu knjigu), stoji nešto ovako (prevodim „art“ kao „veština“, i koristim tvoje izraze):
„Rešenje postaje sastavni deo ‘nauke’, a prestaje da bude ‘veština’ kada se za njega utvrdi ‘recept’“.

Opet, da bi se došlo do „nauke“ (u DEK smislu), neophodno je da se iskoristi „veština“ — zatim, „nauku“ (od „naučeno“, zar ne?) mogu koristiti i oni koji nisu „vešti“ za rešavanje problema.

I baš po ovom kriterijumu, ja mislim da je matematika najbliža „nauci“ — gomile ljudi već koriste izvode, integrale, i još mnogo šta, a da ne poseduju „veštinu“ za rad sa njima, već samo znaju „nauku“.


Znači, ja bih nauku opisao pomoću jednog uslova: „iz istih početnih uslova, uvek se dobija isti rezultat na osnovu te nauke“ — pa sad, izvolite i uklanjajte sve ostale kvazi-nauke iz spiska ;-)

Eh znam da ce zvucati kao slihtanje, ali odavno sam shvatio da Danilo se jedini udubi u sustinu :).

Naravno da znam da se izucava, cak sam i ja na postdiplomskim polagao puno toga, ali je pitanje da li se koristi u praksi :).

Neki cak i Knutov The Art of Computer Programming prevode sa "Umesnost programiranja".

Doduse i po mojem i po tvojem stavu malo koja od ostalih "nauka" je nauka, vise su zanati :).

Ali da se vratimo na matematiku :). Koji bese alat koji koristi matematika (logiku) da nije to zajednicno za sve oblasti mateamtike.

Pa jeste ali nije to zajednicko samo za sve oblasti matematike vec za sve nauke uopste. Nije problem u metodu koji matematika koristi nego to za sta ga koristi odnosno sta proucava matematika. Mada izgleda da na to nema odgovora i zato matematika nije nauka jer ne mozes da kazes sta proucava. Recimo neko moze da kaze da proucava odnose izmedju objekata a ako su nam recimo objekti tacke, prave i slicno opet ce i taj odnos biti razlicit u zavisnosti koje smo aksiome uzeli pa tako imamo Euklidsku, geometrija Lobacevskog ili Rimanovu geometriju...Znaci u matematici ne mozes da kazes sta proucavas jer cesto ti „izmislis“ to sto proucavas tako sto npr. sam „izmislis“ aksiome.

Matematika sigurno nije iznad nauke nego ispod jer nauke koriste matematiku. Matematika je jezgro (kao low level programski jezik) a nauka je omotac (high level)...

Pa i fizika proucava sve i svasta pa se zna :))) ili ja bar mislim da se zna.

Naucnu oblast mozemo izlovati ili po objektima koje proucava ili po metodama zar ne.

Matematika jeste nauka, a mozda cak i jedina nauka, a ostalo je mozda samo prosti eksperiment i zapisivanje ...

Racunarstvo je u ovom trenutku kao biologija, napises probas i mislis da radi :))).
Samim tim nema nauke :).

Jeeeeeeee pa oduvek sam znao da je fizika ustvari matematika, a stalno mi svi govore da ja ne znam fiziku :)))).

Uzgred jel znate zasto ljudi upisuju matematiku ? Pa da znaju fiziku upisali bi ETF.

Matematika je umetnost davanja istog imena razlicitim stvarima.

Matematika je svugde oko nas i ne moze se reci zapravo sta je matematika, i nikada se nece moci reci jer je matematika posebna nauka, nauka iznad svih ostalih nauka.

Bojan Bašić: nemoj celu poruku pisati crvenom bojom!

Prvo moras napraviti razliku izmedju prirodnih nauka i matematike. Matematika nije prirodna nauka. Fizika je filozofija prirode i pojava koje se u njoj desavaju, dok se matematika ipak bavi necim manje opipljivim.

Aham, a ja mislio da matematika lepo opisuje neke delove prirode, recimo brojeve :), ili recimo odnose povrsina, cak nekako i mislim da matematika se i bavi ekstraktom prirode, ne tako opipljivo kao ostale prirodne nauke. I sta je to manje opipljivijem od brojanja :).

I dalje mislim da je pitanje sta je to matematika veoma slozeno, cak slozenije od toga da se opise cime se bavi matematika :).

Profesor Djuro Kurepa koji je nekad radio na PMF u Beogradu govorio je:"Osnovna literatura za svakog matematicara je gramatika Srpskog jezika". Veoma je bitno izrazavanje svakog matematicara. Ali takodje bitno je i znati citati matematicki tekst. Postoje ljudi koji umeju da citaju iz kamena. Gledaju tako u neki kamen i komentarisu kroz koje je sve etape u istoriji on prosao. Ali ipak citanje iz kamena je mnogo lakse od citanja matematickog teksta. Matematika je sve i nista. Sto ce znaciti, budite matematicari ma sta to znacilo, a da se jos uvek tako zove.

Takav pristup je mistifikatorski (kada neko zeli da pokaze kako je bas pametnica, on moze ili da bude pametnica ili da mistifikuje do kraja svoje delo). Naravno mislim da je profesor Kurepa mislio i na matematicku logiku kao i na preciznost izrazavanja. Ali i dalje smatram da ni jedan matematicar nije u stanju da objasni nekom osnovcu cime se on bavi.

A to je ono sto me malo boli, ispada da cak i svestenici mogu da kazu cime se bave, a mi ne mozemo.

Zen i Taoistički sveštenici takođe ne mogu da kažu čime se bave, pošto znaju da svaki pokušaj objašnjavanja maši, pa zato oni koriste analogije ili negativne odrednice da bi sledbenike naveli na trag koji bi im omogućio da sami pronađu odgovor.

Kod matematike je, čini mi se, problem u tome što je ne možeš ograničiti, odnosno svaka definicija matematike bi trebala da počne sa "Koliko nam je za sad poznato, ..." ili "U ovom trenutku, ...". Ali, to je bolno, uvredljivo i netačno, s obzirom na univerzalnu suštinu matematike, koja nije nauka koja otkriva nepoznato o pojavnom svetu, nego slobodno gradi u prostoru ideja (ponekad, tj. vrlo često, radi simulacije dela pojavnog sveta, što je čest izvor zabune oko njene prirode), tako da je možda bolje ostaviti pitanje definicije otvorenim (makar za sad), zbog naših subjektivnih ograničenja.

Ljudi verovatno nisu oduvek imali takve glavobolje oko definisanja matematike. U stara vremena, ljudi su u osnovnim školama učili "račun" (aritmetiku) i za njih je to bila sva matematika koja postoji. Kada su ljudi uopšte shvatili da je matematika univerzalna, odnosno da će uvek postojati mogućnost dodavanja novih oblasti? Da li su to još starogrčki matematičari znali, ili je to od skora?

Pa da, svodi se na nacin spoznaje istine, da li prihvatamo platonov model po kojem sve postoji, a mi samo otrkivamo to sto posotji nezavisno od nas (jelte niko nista nije izmislio, ali jeste otrkio, samim tim naucna otkrica ne bi trebalo da se prodaju :))) ).

Sve u svemu, na kraju mi se cini da ipak ni mi koji se bavimo matematikom, ne znamo cime se bavimo, pa se moze zakljuciti da se ne bavimo nicim :) (nista i nista su nista, dakle crva nikada nije ni bilo).

Eto i odgovora na poslednje, pitanje, znali su odavno da mi samo otkidamo parce po parce sveukupnog saznjanja, i cesto se zaletimo da nesto uradimo, a ono to nemoguce ;)))).

Ajde da spomenem opet jedan lep zadatak, ko ga resi, neka ide da se ubije:

Lenjirom i setsarom za zadatu duzinu ivice kocke konstruisati ivicu kocke koja ima duplo vecu zapreminu.

Prosto se namece, ako ne moze da se redi lenjirom i sestarom, a znamo da postoji, cime moze ?

U, za ovaj problem je ponudjena ogromna nagrada, cini mi se.

Ne mozes da definises nesto sto ne znas sta je. Matematika je jedna ogromna hrapava lopta, a mi je grickamo. I najveci matematicari sveta su grickali samo po povrsini ( i to po slobodnoj proceni, 1/1.000 poluprecnika) Daleko smo od spoznaje, mnogo daleko.

Evo i moje teolosko-prog. definicije
if (fPostojiBog)
Matematika=Nacin Boga da nam kaze da postoji
else
Matematika=Dokaz da tehnika uvek moze vise, bolje i da ide napred uopste

Moja poenta je bila (trebala da bude) da je matematika otvorena, odnosno da je matematičari stvaraju a ne otkrivaju, tako da nema ne samo šanse već ni teorije da se ona ikada iscrpi.

Rekao bih da je i npr. fizika "otvorena" nauka. Ali ćemo uvek znati da raspoznamo matematičko otkriće od bilo kog drugog - to znači da svi vrlo dobro znamo šta je matematika :)

U Matematiku svakako spadaju sve njene oblasti, pri čemu tu ima i oblasti koje (za sada) nisu primenjene nigde van Matematike, a recimo u Matematici su pomoću njih rešeni neki fundamentalni matematicki problemi. No, ako vas interesuje samo primenjena Matematika, onda je to stvar vaših interesovanja. Ne možete reći da je Matematika samo onaj njen deo koji vas zanima!

Daleko od toga da se Matematika bavi samo količinama i prostornim odnosima. To se u stvari može reci za Matematiku do početka XIX veka i pojave Galoaove teorije. Za "dogaloaovsku" Matematiku savremeni matematičari često cinično kažu da se bavila "prebrojavanjem ovaca na livadi". Ako želite da dođete do odgovora na pitanje šta je Matematika (danas), ne možete "živeti" u XVIII veku!

Evarist Galoa (Evariste Galois 1811-1832) je baveći se problemom rešivosti algebarskih jednacina

a_n*x^n+...+a_1*x+a_0=0, a_n<>0

preko operacija sabiranja, oduzimanja, množenja, delenja i korenovanja proizvoljnog stepena u kompleksnom području uveo tada potpuno nov matematički pojam -- grupe, koji nije niti geometrijskog niti numeričkog tipa! On je dokazao da postoje algebarske jednačine petog i višeg stepena čiji se koreni ne mogu izraziti preko pomenutih operacija ako kao konstante koristimo samo koeficijente a_0,...,a_n. Jedna od takvih jednačina je

x^5-5x+1=0.

Tu teoremu je pre njega dokazao Nils Abel, ali je Galoa otkrio opštu teoriju (koja po njemu nosi ime) koja je celu tu problematiku rasvetlila. Galoa nam je poznat po samo jednom otkriću, ali se zahvaljujući tom otktiću naziva "ocem moderne Matematike" jer se smatra da je "odlepio" Matematiku od onoga što se često cinično naziva "prebrojavanjem ovaca na livadi". To otkriće se smatra jednom od najvećih revolucija u istoriji Matematike. Sama nerešivost opšte algebarske jednacine petog i višeg stepena na pomenuti način i nije toliko značajna, koliko je značajno otkriće pojma grupe sa obzirom na činjenicu koliki je uticaj to otkrice imalo na Matematiku.

U srodne probleme spadaju i neki problemi konstruktibilnosti geometrijskih objekata lenjirom i šestarom koji su postavljeni još u staroj Grčkoj, a koji su rešeni, i to negativno (dokazom da je tražena konstrukcija nemoguća) algebarskim metodama u XIX veku. Danas se rešenja tih problema izlažu upravo u svetlosti teorije Galoa. Kasnije je Galoaova teorija uopštena i na druge vrste jednačina, kao što su diferencijalne, pa se tako danas zna za neke diferencijane jednačine da nisu rešive preko kvadratura (integracija).

Na neki ančin od starih grka nam potiče još jedan veliki problem -- problem paralelnosti. U Euklidovim "Osnovama Geometrije", koje su danas zbog pogrešnog latinskog prevoda grčke reči "stoiheja" poznatije kao Euklidovi "Elementi", nalazimo najstariji pokušaj aksiomatizacije (sistematskog zasnivanja i izlaganja) jedne teorije koji je stigao do nas. Ta Euklidova sistematizacija je dugo (sve do XIX veka) bila njbolji udžbenik Geometrije, kao i najbolji uzor za sistematsko izlaganje neke naučne ili filosofske discipline. Euklidovi "Osnovi Geometrije" su bili uzor Dekartu za sistematsko zasnivanje i izlaganje Filosofije, Njutnu Mehanike (čuveni "Matematički principi Fizike"), Spinozi Etike i tako dalje. Zanimljivo je još pomenuti da su sve do XX veka tri najčitanija dela bili Bublija, Danteova "Božanstvana komedija" i Euklidovi "Osnovi Geometrije" (ispred Kurana na primer). Naravno, Biblija se još uvek "drži" na prvom mestu.

Poznato je da se ni jedan stav ne može u potpunosti dokazati. Naime, ako bismo hteli neki stav da dokažemo u potpunosti, sam njegov dokaz bi se, kao što to mora biti, pozivao na neke činjenice, to jest argumente. No, dokaz će u tom slučaju biti valjan samo ako su ti argumenti valjani. To znači da ako želimo da budemo dosledni u dokazivanju u potpunosti stava koji želimo da dokažemo, morali bismo da dokažemo i te činjenice na koje smo se pozvali u dokazu, kao na argumente. Međutim, u dokazima tih drugih činjenica pozvali bismo se na neke treće, koje bismo ako hoćemo da budemo dosledni u dokazivanju stava koji želimo da dokažemo takođe morali da dokažemo. Ova priča ima tri moguća nastavka.

1. Proces dokazivanja se nikada ne završava. U tom slučaju stav nećemo nikada ni dokazati.
2. Na nekom mestu se poziva na stav koji se dokazuje preko stava koji se na tom mestu dokazuje. Ovo je klasična logička greška koja se zove "začarani krug" (circulus viciosus). U tom slučaju stav nećemo dokazati jer dokaz nije valjan.
3. Na nekom mestu se zaustavljamo i prihvatamo neke stavove bez dokaza. Ukoliko nismo napravili nijednu grešku, stav koji dokazujemo će važiti pod uslovom da važe svi stavovi koje smo usvojili bez dokaza. Drugim rečima, polazni stav smo dokazali do na te stavove, odnosno izveli smo ga iz njih.

Uobičajeno je da se treći put bira kao najprihvatljiviji. Neko može reći: "Ali zar stav nije dokazan u potpunosti, budući da su ti stavovi (koji nisu dokazani) krajnje jednostavni, očigledni i jasni?". Prvo, mi čak i ako smatramo neki stav koji nismo dokazali krajnje jednostavnim, očiglednim i jasnim, mi moramo prihvatiti činjenicu da taj stav nismo dokazali, a samim tim da nismo u potpunosti dokazali ni stav koji smo izveli iz tog (nedokazanog stava). Drugo, istorija Matematike nas uči da mnogi očigledni stavovi nisu tačni. Tu posebno treba istaći Peanove kontinuume u Paradoksalne dekompozicije Banaha i Tarskog.

Znači, nijedan stav ne možemo u potpunosti dokazati, pa moramo da se u procesu dokazivanja negde zaustavimo i prihvatimo neke činjenice bez dokaza. No, tu se odmah postavlja pitanje kriterijuma gde treba stati. Prvi kriterijum koji se nameće je da se zaustavi na krajnje jednostavnim, očiglednim i jasnim stavovima. No, uz prethodnu kritiku pojma očiglednosti treba dodati da je ovakav kriterijum krajnje subjektivan, jer ono što je jednom čoveku krajnje jednostavno, očigledno i jasno, drugome ne mora biti ni jednostavno, ni očigledno, ni jasno. Stoga se može u procesu dokazivanja zaustavljati na jednom, unapred dogovorenom skupu stavova koji se neće dokazivati. To su takozvani polazni stavovi ili aksiome. Stavovi koji se iz njih izvode se zovu teoreme. Tako se rešava problem subjektivnosti kriterijuma izbora stavova na kojima će se proces dokazivanja zaustavljati.

Iz sličnih razloga se ne mogu ni svi pojmovi definisati (definitio -- završiti), to jest ne može se za svaki pojam dati potpun kriterijum kada nešto pripada tom pojmu, a kada ne. Stoga se neki pojmovi ne definišu, već izdvajaju kao polazni, a ostali se definišu preko njih. Pojmove koje definišemo preko polaznih zovemo izvedenim pojmovima.

Iz tih razloga je Euklid izdvojio neke stavove kao polazne (aksiome i postulate) i iz njih izvodio ostale. No, postavilo se pitanje da li se peti Euklidov postulat može izvesti iz preostalih postulata i aksioma. Taj problem se naziva problemom paralelnosti. Do odgovora (negativnog) došlo se u XIX veku otkrićem modela u kojima važe sve aksiome i svi postulati izuzev petog. Prethodno su Lobačevski i Boljaj nezavisno jedan od drugog došli na ideju da je tako nešto moguće. To otkriće takozvanih neneuklidskih Geometrija je odlepilo Geometriju od empirije i time je Geometrija prestala da "robuje" Fizici kao disciplina koja proučava prostorne odnose u spoljašnjem (fizičkom svetu).

U poslednjoj četvrtini XIX veka Kantor (Georg Ferdinand Ludwig Philip Cantor) otkriva teoriju skupova. Ona se toliko svidela matematičarima kao zgodan jezik za izlaganje Matematike da je David Hilbert rekao "Iz raja koji nam je Kantor napravio, niko nas nikada neće isterati." (Aus dem Paradies das Cantor uns geschaffen, soll uns niemand vertreiben können). No, u Kantorovoj teoriji skupova su otkrivene protivrečnosti. Najjednostavniji paradoks je bio Raselov. Koristio je samo "nešto malo" logike i aksiomu komprehenzije (okupljanja) koja glasi

"Za svaku unapred datu osobinu P(x) postoji skup čiji su elementi tačno oni x za koje važi P(x)".


Taj skup se obeležava sa {x:P(x)}. Uočimo osobinu P(x) definisanu sa

P(x) <=> (x je skup i x ne pripada skupu x)


Tada za skup A={x:P(x)} važi

x pripada skupu A <=> (x je skup i x ne pripada skupu x).


Ako x jeste skup, to se svodi na

x pripada skupu A <=> x ne pripada skupu x.


Zamenjujući x sa A dobijamo da važi

A pripada skupu A <=> A ne pripada skupu A,


a to je kontradikcija budući da ni jedan iskaz nije ekvivalentan svojoj negaciji (ne(p<=>ne p) je tautologija). Onda su matematičari pokušali da "spasu" teoriju skupova na razne načine, i tako su nastali razni pravci u Matematici koji daju različite odgovore na osnovna pitanja Filosofije Matemetike među koje spada i pitanje šta su matematički objekti. Neki od pravaca su formalizam, logicizam, realizam, platonizam i intuicionizam, o kojima ne mogu ovde da pišem (barem ovaj put). Danas se Matematika uobičajeno izlaže u okviru aksiomatske teorije skupova ZFC koja je zasnovana na predikatskom računu prvog reda i u kojoj do sada nije otkrivena ni jedna protivrečnost.

Stvari su se dodatno iskomplikovale kada je Gedel (Kurt Gödel) u prvoj polovini XX veka otkrio da bilo kakav eventualni pokušaj formalnog zasnivanja Matematike koji bi dopustio opsivanje iole ozbilnijih fragmenata Matematike nepotpun. Štaviše, ne može se nikako upotpuniti dodavanjem niovih aksioma tako da ostane neprotivrečan i da pitanje da li je nešto aksioma bude algoritamski rešivo. Jedno od najpoznatijih matematičkih tvđenja za koje je dokazano da nije niti dokazivo niti opovrgljivo u sistemu ZFC je kontinuum hipoteza (CH) koja klasi

"Ne postoji skup A takav da se niti skup realnih brojeva može 1-1 preslikati u skup A, niti da se skup A može 1-1 preslikati u skup prirodnih brojeva".

Gedel je 1938. pronašao model koji zadovoljava sve aksiome teorije skupova i u kome važi CH, a Koen (Paul Cohen) je 1963. pronašao model u kome važe sve aksiome teorije skupova i u kome ne važi CH. To znači da CH uopšte ne zavisi od sistema aksioma ZFC. Što se tiče polja realnih brojeva koje je definisano kao uređeno polje koje zadovoljava aksiomu supremuma, taj opis itekako počiva na pojmu skupa za koji, kao što vidimo, nemamo potpun opis. Stoga nije do kraja rečeno ni šta su realni brojevi. Zapravo, dokazuje se da je opis strukture realnih brojeva preko skupova potpun do na skupove, za koje imamo samo delimičan opis. Takođe, postoje i sasvim drugačija zasnivanja Matematičke Analize kao što su Nestandardna Analiza i Glatka Infinitezmalna Analiza.

No, pravi problemi nastaju kada se stigne do nekih dubljih hipoteza iz teorije skupova za koje više nije sigurno ni da li predstavljaju matematička pitanja jer nije jasno na šta se odnose, budući da se pojam skupa ne može nikada sa svih strana rasvetliti. Ovim i dalje nije dat odgovor na pitanje postavljeno na početku, već je samo ukazano da se u traženju odgovora na to pitanje sve ove činjenice (kao i mnoge druge o kojima ne mogu ovde i sada da pišem) moraju uzeti u obzir. Takođe, odgovor na to pitanje nije jedinstven. Svaki od pomenutih pravaca daje po jedan odgovor i ti odgovori nisu međusobno ekvivalentni, pa čak ni saglasni. To je posledica činjenice da svaki od tih pravaca predstavlja jednu (od ko zna koliko mogućih) koncepcija zasnivanja Matematike. Drugim rečima, Matematika nije jedna ako pod Matematikom podrazumevamo ono što matematičari podrazumevaju pod tim pojmom, već u tom smislu postoje razne "Matematike".

Ovde se mnogo prica o matematici u superlativu kao majka svega ostalog i svih ostalih nauka, ja iako cenim ovu nauku (vestinu, umetnost) ne bih otisao dalje od toga da je matematika filozofski sistem izgradjen na pretpostavci da postoje tacka i skup, sto je vremenom pokazalo jako zgodne rezultate i implikacije. Sve ostale grane matematike se posle suzavaju ka nekom konkretnijem cilju uvodjenjem dodatnih pretpostavki...

Pa nije bas tako, cak i euklid u elemntima uvodi i prave i ravan i tamo neke relacije :).

Mozda je preciznije pitanje: sta je zajednicko za sve te oblasti matematike ?

Da li je to nacin rezonovanja ? ili pak nesto drugo .

Pa element skupa (npr tacka) i skup. Euklid uvodi pravu i ravan, ali je to (uglavnom) nepotrebno za sabiranje brojeva 2 i 3, t.j. to je uvodjenje dodatnih definicija za konkretizovanje problema (ili pak resenja). Sa druge strane Euklid je pretpostavio (definisao) jos par stvari za koje je Lobocevski utvrdio da se ne mogu uzimati zdravo za gotovo. Neko moze reci da je ocigledno da je 1+1=2 ili da prostor ima 3 (4) dimenzije ili da se dve paralelne prave ne seku, na matematici je da na osnovu datih pretpostavki razradi posledice, ali i da postavi potpuno drugacije polazne osnove. Do Kosija su vazili termini dovoljno malo (veliko) i onda tako otprilike se dovoljno mnogo puta saberu dovoljno male velicine, pa se dobije integral sto je bilo zasnovano na pretpostavci da se podrazumeva koliko je to dovoljno. Onda dodje Kosi i isproziva ih da nisu normalni. Sticem utisak da je razvoj matematike ustvari samo odbacivanje "ociglednih" stvari.

Sad sam se vec pogubio i ne znam sta hocu da zakljucim ovim postom. Kad se smislim nastavicu.

Eh, pazi, neke oblasti matematike mogu da se zasnuju bez skupova, uostalom sta su koristili pre otrkica skupova :).

Ali ajde, probaj da se izvuces.

Mada ja i dalje mislim da je matematika sve ono sto se koristi specificnim naucnim metodama (a koje me mrzi da opisujem sada :))) )

Zar nije paradoks vec u postavci? Odnosno meni vec ovo nema smisla, mozda ne kapiram kako valja........

Pa prica o Raselovom paradoksu je malo dugacka, naravno da treba prvo uvesti skupove, pa ...

Nedeljko sigurno zna bolje celu pricu i sa razresenjem koji nosi 20-ti vek :).

Hm ne znam, ali na ovih pet matematika sto su me na ETF-u ucili, sve je bilo, na ovaj ili onaj nacin, preko skupova, pa sam mislio da to mora tako. Osim toga i ako nesto moze da se definise bez skupova (sigurno dosta stvari moze) stekao sam utisak da matematika se mnogo ne trudi da se bavi time (opet iz svog iskustva). Mada se to opet moze objasniti Nedeljkovim postom, gde se kaze da su matematicari mnogo zgotivili teoriju skupova, pa sve preko toga objasnili.

Bez ljutnje, ali matematika na ETF-u je kao elektronika na Matematickom, dakle nikakva :). Dobro nije bas nikakva, ali je vise inzinjerska matematika, prakticna vise, a manje filozofija :).

Secam se jednog diplomca ETF-a koji je pisao neki rad i pise: (nesto ne uspevam TeX...)

(\forall x)\land(\forall y)...

Ima nesto dublje od skupa, a to je nacin razmisljanja, uostalom cela matematika se da izgraditi nekim drugim sredstvom a ne skupom, samo ko to zeli da radi :))).

Ne znam koje sam to superlative koristio u svom postu. Samo sam hteo da ukažem na neke činjenice koje se moraju uzeti u obzir pri traženju odgovora na postavljeno pitanje.

Raselov paradoks je zapravo bio paradoks u Fregeovom formalnom logičkom sistemu koji je dopuštao definiciju takvog skupa. No, to takože znači da ni sistem aksioma Teorije Skupova ne sme da dopusti tako nešto.

Danas se Matematika tipično zasniva preko aksiomatske Teorije Skupova ZFC koja se oslanja na predikatski račun prvog reda. Predikatski račun prvog reda takođe može da se uvede aksiomatski. Međutim, problem je u tome što je sistem aksioma ZFC teorije skupova nepotpun. O tome sam pisao u delu posta koji se bavi koninuum hipotezom.

Dakle, pretpostavke na kojima počiva Matematika su (zasad) izražene aksiomama i pravilima izvođenja predikatskog računa prvog reda i aksiomama Teorije Skupova, a ne na pretpostavci da postoje tačka i skup.

Ako bi pretpostavio da postoje tačka i skup, to bi bilo isto kao da si pretpostavio da postoje mačka i miš, budući da nisi rekao šta je to tačka, a šta ravan. Zapravo, aksiomatikom ti opisuješ neke polazne pojmove. To su oni pojmovi koji se ne definišu. Aksiomatika samo daje neke veye između njih, ali ne daje odgovor šta su oni.

Recimo u aksiomatskom sistemu koji su predložili Borsuk i Šmileva za euklidsku Geometriju osnovni (polazni) pojmovi su tačka, prava, ravan, relacija incidencije između njih, relacija izmađu na trojkama tačaka i relacija podudarnosti parova tačaka na četvorkama tačaka. Još je Hilbert primetio da nam takvi aksiomatski sistemi (imao je i on jedan) ne daju odgovor na pitanje šta su tačke prave i ravni. To su neka "tri sistema stvari", koji mogu biti i slonovi, čaše i stolovi, samo ako između njih uspostavimo pomenute relacije incidencije poretka i podudarnosti tako da budu ispunjene sve aksiome.

U odnosu na druge nauke, Matematiku karakteriše njen metod: dedukcija. Matematika je jedina disciplina koja koristi isključivo dedukciju kao metod zaključivanja. Između dedukcije i matematičkog metoda se može staviti znak jednakosti.

Nasuprot onome što piše po mnogim školskim udžbenicima Filosofije, ali ne i u udžbenicima za Filosofski Fakultet u Beogradu, dedukcija je ono zaključivanje kod koga zaključak nužno sledi iz pretpostavki, ili narodnim jezikom rečeno, koji ne može da "omane". Svaka matematičkla teorema je oblika "Pod tim i tim pretpostavkama važi to i to" u smislu da to mora UVEK (nužno, neizostavno) da važi. Tu se često neke pretpostavke ne navode jer se podrazumevaju. Recimo, u teoremama iz analize se podrazumevaju pretpostavke vezane za Logiku, skupove i relane brojeve. Ovde naglašavam da deduktivan pristup ne mora biti aksiomatski, mada su te dve stvari jako tesno povezane.

Dakle, deduktivno zaključivanje je svako "100% pouzdano zaključivanje". E, tu se odmah nameće problem kako mi znamo da je neko zaključivanje deduktivno. U suštini, ništa se ne može potpuno dokazati, pa ne možemo ni biti sasvim sigurni da je neko zaključivanje deduktivno.

Mi možemo reći: "Pa ako se u nekom formalnom sistemu formalno izvede neka formula, nećemo sumnjati u ispravnost tog izvođenja ako smo ga proverili". Drugim rečima, nećemo na primer sumnjati da su dva niza znakova jednaka ako smo ih pročitali znak po znak i utvdili jednakost tih nizova znakova. Ovo je pristup vrlo blizak pameti, da prihvatimo ono što se može algoritamski proveriti, ako smo takvu proveru izvršili. Tada se možemo uveriti da je neki niz znakova formalno izvodiv u nekom formalnom sistemu.

Da ne bi ispalo da koristim suvišne superlative, naglasiću da ograničavanje na SAMO deduktivno zaključivanje ima svoje prednosti i mane. Prednost se sastoji u činjenici da nemamo pouzdaniji metod. Matematika je jedina ozbiljna nauka čiji nijedan stav nikada nije opovrgnut. Ne, ni Neeuklidske Geometrije nisu nijedan stav opovrgle, već samo pokazale da peti Euklidov postulat nije posledica ostalih aksioma i postulata. Mana ovakvog pristupa je što se na taj način može proučavati samo dedukcija, i ništa više.

Probejte na primer da dedukujete boju svog pisaćeg stola, odnosno, da vas neko zatvori u mračnu sobu u koju nikakvi signali ne dopiru, i da bez ikakvih informacija o stolu "čistim mozganjem" zaključite koje je boje. Ko misli da to može, neka mi kaže koja je boja mog pisaćeg stola.

Evo, upotrebiću, čak dva superlativa. Dedukcija je nalik na pušku koja "ne omašuje", ali koja ima kraći domet od svih ostalih pušaka. Ostale puške gađaju dalje, ali ponekad "omašuju".

Inače, do Košija se radilo sa beskonačno malim veličinama (infinitezimalama), kao i sa beskonačno velikim. Koši je učestvovao u eliminisanju istih uvođenjem pojmova dovoljno malog i dovoljno velikog.

Da, Čupko je u pravu da je Matematika mnogo starija od skupova. No, u pomenutoj teoriji ZFC je Matematika zasnovana na mnogo strožiji način nego što je bila ranije. Ipak, postoje i drugi načini isto toliko preciznog zasnivanja Matematike koji su čak ekvivalentni sa pomenutim. Jedan od njih je Teorija Kategorija.

U stvari, odgovor na postavljeno pitanje je odavno dao Branko Kockica.

Vratio sam se sad sa Elektrijade, ETF je drao u svim predmetima, osim u matematici, gde su ubedljivo prvi bili Novosadjani (u i 1. i u 2.).

Da dodam i ja nesto sto sam skoro nasao na netu

"Ako ne znas matematiku, znaces matemotiku" :)))

Veoma je logicno da na elektrijadi ETF bude dobar :), bese na elektrijadi ne ucestvuje FON ? a da ne spomenemo MatF ?

Nu, dakle cinjenica je da imamo razne nivoe proucavanja matematike, ja bi podelio po skolama:

-nivo osnovne skole, nizi razredi
-nivo osnovne skole, visi razredi
-nivo srednje skole
-nivo tehnickih fakulteta
-nivo matematickih fakulteta

Naravno svaki nivo ima svoju definiciju matematike :).

Secam se kada mi je Doblilo Tosic na etf-u predavao matematiku pa kada je bas pominjao razlike u ucenju matematike izmedju etf-a i pmf-a.
Recimo kada resavamo diferencijalnu jednacinu etf-ovac nikada ne bi trebalo da prvo dokazuje da resenje postoji itd...Zasto?

Zato sto ako je izlaz nekog uredjaja uslovljen nekom diferencijalnom jednacinom ne treba da gledamo da li resenje postoji jer to bi znacilo da ni izlaz ne postoji. Ako postoji neki izlaz koji je resenje neke diferencijalne jednacine onda resenje postoji.

Jos dosta stvari je pominjao ali ne mogu da se setim. Strasno dobar profesor. Mislim da je najbolji profesor na etf-u. On bas zbog toga sto je znao da neke stvari etf-ovci nece nikada raditi nije zahtevao te stvari. Bolje je to vreme iskoristiti za neke stvari koje su korisnije etf-ovcima...Inace je zavrsio etf i predlagao je da na etf-u predaju samo profesori koji su zavrsili etf i da se svake godine izvlaci koji ce predmet koji profesor da predaje. Na taj nacin ne bi mogao neki profesor da misli da je njegov predmet najvazniji pa da se izivljava.

Ha, ha, ha, to je slicno ovome o cemu sam pricao :-)

Ja se zaista izvinjavam ETF-ovcima, ali pomenuti profesor Matematike na tom fakultetu je JAKO slab matematičar! To se jako dobro vidi na primer iz njegove knjige o Numeričkoj Analizi koja se (barem do skora) koristila na ETF-u.

Nazvati matričnu normu realnim brojem predstavlja matematičku nepismenost! Koliko se ja sećam, matrična norma je FUNKCIJA koja matricama pridružuje realne brojeve. Slažem se da takav propust sam po sebi ne umanjuje vrenost udžbenika, ali ja do sada nisam našao niti jedan dobar matematički tekst koji je pisao neko ko je matematički nepismen. Drugim rečima, takvi po pravilu prave i suštinske greške.

Da, znam da će mnogi reći da svi ljudi greše, ali postoje vrste grešaka koje se prave ISKLJUČIVO iz neznanja. Ovakav lapsus (ako neko smatra da ovu grešku treb atko nazvati) ne možete naći niti kod jednog ozbiljnog matematičara.

Pogledajte na primer šta je napisao u napomeni o "anuliranju funkcije f i njenih izvoda u beskonačnosti" kod sumacionih formula za redove primenom Euler-MacLaurin-ove formule bez ikakve pretpostavke o funkciji f. Uzmite na primer funkciju 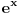. Pa i da se anuliraju, kakve bi to imalo veze sa konvergencijom reda na desnoj strani jednakosti? Posmatrajte na primer funkciju 1/ln(x). Drugim rečima, Matematika kao i sve ostalo, se ne može naučiti od nekoga ko je ne zna.

Inače, po zakonu o univerzitetu, univrezitetski profesor ili asistent možete biti samo iz onih oblasti za koje je matičan onaj fakultet koji ste završili. Na primer, ne možete biti sa Mašinskim Fakultetom asistent ili profesor iz programiranja, iako se i tamo uči nekakvo programiranje. Recimo, za oblast Informatke su trenutno matični fakulteti ETF, Matematički Fakultet i FON.

Nekada je ETF bio matični fakultet za oblast Matematike zajedno sa Matematičkim. To ne bi bilo toliko loše da ETF nije proizveo seriju invalida znanja iz oblasti Matematike sa titulom doktora matematičkih nauka, kao što su Dušan V. Slavić, Dragoš Cvetković i Dobrilo Dj. Tošić, uz tek poneke svetle izuzetke kao što je Dr Milan Merkle (ostali prozvani ne zaslužuju prefiks Dr).

Pokojni Dušan V. Slavić je najčuvenije ime Numeričke Analize u istoriji ETF-a. Mnogi "matematičari" sa ETF-a obilato citiraju njegova "naučna otkrića". Čak je i on sam u članku posvećenom metodima tangente u nekom prastarom broju Računara (mislim da je u pitanju broj 13) napisao da je on otkrio metod konjugovanih pravaca 1986. godine. Inače, pomenuti metod je bio otkriven još 1950. i bio je vrlo poznat kao metod kojim se u n iteracija rešava TAČNO proizvoljan sistem od n nelinearnih jednačina sa n nepoznatih pod uslovom da su sve nelinearnosti kvadratne. Takva "neobaveštenost" nije dopustiva za nekoga ko nosi titulu doktora matematičkih nauka, uža oblast Numerička Analiza, a pogotovu nije opravdanje za nazivanje tog metoda "svojim otkrićem".

Da, znam i ja da je do mnogih otkrića dolazilo više ljudi nezavisno, ali ovde se radio o vrlo poznatoj metodi, a i ako je zaista bio toliko "neobavešten" i došao do slične ideje kako da reši neki problem, odakle mu ista ideja kako da nazove metodu? Tu već ima previše koincidencije! Njutn i Lajbnic jesu nezavisno otkrili diferencijani i integralni račun, ali su imali potpuno različitu terminologiju i potpuno različite oznake.

No, u tom članku Dušan V. Slavić tvrdi da Njutnov metod tangente ima red konvergencije 2 (što je tačno), a da metod sečice ima red konvergencije 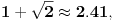koji je stoga veći od reda konvergencije metode tangente. Nije toliko strašno to što je taj rezltat numerički pogrešan. Tačno je da red konvergencije metode sečice iznosi 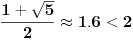. Strašno je to što je obrnuo redosled redova konvergencije dveju najpoznatijih metoda.

Ja mogu da shvatim da neko zaboravi tačan podatak takve vrste, ili da ga zameni sa nečim drugim, ili da pokuša da ga izračuna, pa negde pogreši u računu. Recimo, ne bi bilo uopšte stašno da je naveo koren iz tri kao red konvergencije, ili nešto što je manje od dva, to jest nešto što može biti red konvergencije te metode. Najblaže rečeno, ovo je kao da je kao rezultat intergracije pozitivne funkcije na intervalu [0,1] naveo -5!

Zamislite da odete kod eksperta za kola, i da on počne da vam priča kako maksimalna brzina Pežoa 603 iznosi 250 Km/h, a da maksimalna brzina Juga 55 iznosi 320 Km/h! Šta biste vi pomislili osim da taj čovek nema predstavu o onome o čemu priča? On može da ne zna tačne tehničke podatke vozila, ali ne može da zameni redosled dva popularna modela po pitanju maksimalne brzine, ako je ta razlika značajna. Pomenuti metodi predstavljaju dva najpoznatija metoda za rešavanje nelinearnih jednačina.

A Dragoš Cvetković je postao akademik SANU iz oblasti Matematike na osnovu velikog broja "naučnih radova" od kojih mnoge mogu popularni matematički programi na Pentiumu I na 233 MHz da reše za kraće vreme od onog koje čovek može da registruje.

Ja se zaista izvinjavam, posebno Filmilu i Srkiju koji su na ovom forumu pokazali da imaju klikere za Matematiku, a završili su ETF, kao i ostalim postiocima ovog foruma koji su završili ETF. Uz svo njihovo uvažavanje, mislim da te klikere nisu stekli na fakultetu, već da su ih doneli na fakultet položivši vrlo težak prijemni ispit. Ko jednom ima klikere, uvek ima klikere.

No, ovo sam morao da napišem jer me je Srki "vukao za jezik" ne samo pričom o "Velikom" profesoru Dobrilu Dj. Tošiću, već i tezom da na tom fakultetu treba da predaju Matematiku samo oni koji su završili taj fakultet. To bi bilo prihvtljivo (zašto da matematički Fakultet nema zdravu konkurenciju) da nije pokazao nekompetentnost za pomenutu oblast.

Odnosilo se na druge postove

Nedeljko, kada sam rekao "dobar" profesor, nisam to rekao u smislu da je dobar matematicar ili ne. Merkle je recimo los profesor. E mozda je bas zbog toga los profesor zato sto kako kazes ima dobro znanje matematike (mada sam i u njegovim knjigama nasao greske koje posle on nije znao kako da promeni).
Ja dam sam hteo da budem matematicar upisao bih PMF ili cu uciti sam sa strane. Na etf-u ne treba da nas uce ljudi kao Merkle ili neki sa pmf-a jer ce oni da nas dave nekim teoremama i stvarima koje etf-ovcima nece nikada koristiti. Zato su Dragos i Tosic dobri profesori a Merkle los. Merkle te tera da ucis dokaze o nekim teoremama o redovima napamet (neke za kje ionako posle zaboravis dokaz i nece ti trebati) i hvata se za svaku rec (ioako negde moze drugacije da se kaze a da ima isti smisao) a manji akcenat daje na koriscenje tih teorema sto je potrebno ljudima koji su na ETF-u. Zato je glupo da me matematici uci profesor sa PMF-a jer je velika verovatnoca da ce da me davi nepotrebnim stvarima. A i nije samo to u pitanju nego profesor sa etf-a ce bolje znati na sta da stavi akcenat prilikom predavanja jer zna sta ce ljudima sa etf-a najvise trebati.

Maltene na svakom fakultetu se uci matematika ali ne treba svima znanje dokaza o konvergiranju svakakvih redova. Ok neka znaju kada red konvergira ali zasto bi nekog sa saobracajnog ili fona maltretirao da uci dokaze napamet kao da je matematicar?

I Nedeljko, zaista nema potrebe da se izvinjavas jer ja uopste ne uzdizem etf i njegove profesore. Imam mnogo vise negativnog iskustva nego pozitivnog. Cak i nisu najgori profesori matematike nego ima i ljudi koji drze strucne predmete a ne znaju da predaju, traze pogresne stvari i losi su profesori. Zato bi bila dobra fora sa izvlacenjem papirica na kraju drugog semestra. Taman lepo imas vremena da pripremis predavanja za vreme raspusta a znaces sta ti najvise treba odatle i neces smatrati da je tvoj predmet najvazniji kao npr. Merkle. Ljudi koji previse znaju cesto imaju potrebu da namecu svoje znanje. Ja sam ionako najvise naucio sam jer kada me nesto zanima ne znaci da isto to zanima i profesora a i lakse mi je sam da potrazim informacije. Narocito je sada to lako uz internet, google, online pristup naucnim zurnalima itd..

Ne razumem ovo?

Pa da se ja malo ubacim, zato je i bitno da se zna sta je matematika, da ne bi ispalo da je ono sto uce recimo na biologiji matematika :). Cinjenica je da je da ETF voli da se igra prakticnog, pa samim tim njihova matematika je skup recepata za uspesno resavanje ... nesto sto su imali arapi odavno :) Gde je tu nauka ? Sto se niko ne seti mog omiljenog profesora sa ETF-a Labana :). Moram priznati da sam kupio njegovu knjigu kao mlad student i da sam posle shvatio da je lepo preveo odabrane zadatke iz Ljaskog :).

Dakle lepo je to sto na ETF-u ima matematike i sto se uci, ali nemojte da je dizete u nebesa, uostalom na svim fakultetima postoji Engleski kao predmet, pa ipak ga predaju samo oni koji su zavrsili Fililoski faks :).

A da, i jos jedna nepravda, ETF je dosta bio proteziran od vlasti (raznih, pa mozda i od ove sada) jer je privredni fakultete za razliku od Matematickog bez kojeg se moze, deci ce predavati matematiku ionako oni sa uciteljskog fakulteta :). Uostaliom pogledajte cene skolarina :).

Ma naravno! Ja nemam neko posebno misljenje o matematici sa etf-a. Vise sam naucio sam ono sto me najvise zanima i ono sto mi treba. Da me nesto vise zanima matematika upisao bih PMF.

Ja o Merkleu nisam piso na osnovu njegovih udžbenika za ETF, već n aosnovu njegovog naučnog rada. Moguće je da je Merkle loš profesor. Ne znam. Izgleda da je dobar matematičar. No, znanje ne može preneti neko ko ga nema. Slažem se da na tehničkom fakulltetu matematičari nisu kompetentni za pitanje šta je inženjeru potrebno od Matematike. Za to su kompetentni sami inženjeri. Na ozbiljnim tehničkim fakultetima po svetu Matematiku predaju matematičari, pri čemu sadržaje odabiraju inženjeri, i onda nema učenja nečega što nema veze sa inženjerskom praksom. A evo i razloga zašto se na ETF-u uče.

Po zakonu o univerzitetu, da bi neko bio asistent na univerzitetu na nekom predmetu, mora da ima fakultet koji je matičan za tu oblast. A da bi bio profesor mora da ima Dr iz te oblasti, pri čemu Dr za tu oblast može da izda samo fakultet koji je matičan. Dakle, da bi ljudi sa ETF-om mogli da predaju Matematiku na ETF-u, mora u vreme njihovog diplomiranja ETF da bude matičan za oblast Matematike kao što je nekada bio kada su Tošić i Cvetković stekli potrebna zvanja i titule (dakle, bilo je po zakonu).

Međutim, to tačno znači da je onda diplomirani elektroinženjer ujedno i diplomirani matematičar, kao i da se titula Dr iz oblasti Matematike može steći na tom fakultetu. E, ali onda ne može da se uči iz Matematike samo ono što pripada inženjerskoj praksi. Na ETF-u su studenti pre 1990. učili 300 Kg Matematike jer je trebalo da postanu ne samo diplomirani elektroinženjeri, već i diplomirani matematičari, budući da su sticali sva prava u oblasti Matematike koja imaju matematičari. Da li ti je sada jasnije zašto program Matematike na ETF-u prevazilazi granice inženjerske prakse?

Naravno, nisam hteo da kažem da je ETF neozbiljan fakultet pišići o tome kako se radi na "ozbiljnim" tehničkim fakultetima po belom svetu. Ja zapravo smatram da je ETF takav kakav je izbacivao vrsne inženjere, ali ne i matematičare. Najveći broj studenata ETF-a nikada nije ni imao ambicije za sticanjem zvanja diplomiranog matematičara, ali ih je neko terao da to budu.

Zahvaljujem se svim studentima ETF-a (bivšim i sadašnjim) na razumevanju. Očekivao sam mnogo "oštrije" odgovore, budući da je moj post bio JAKO "oštar", tako da je bila potrebna velika tolerancija da ne bude shvaćen zlonamerno.

Pa cini mi se da mu udzbenici nisu losi. Makar onaj iz verovatnoce. (Napominjem da sam ja njih citao iz pogleda inzenjera a ne matematicara pa nisam obracao paznju na sve detalje).
Njegov udzbenik iz analize nije za etf tako da ga ni nemam. Los je za inzenjeta jer ga preopterecuje sa nepotrebnim stvarima.
Nedeljko, upravu si za strane univerzitete. I ne vazi samo to nego u zavisnosti od smera se rade razlicite stvari iz matematike. Recimo ovde na University of Auckland ako upises smer software engineer ne radis furijeovu i laplasovu transformaciju ali se zato stavlja akcenat na racunanje kompleksnosti algoritma vise i bolje nego na etf-u. Takodje relacije (posto je predmet 'baze podataka' obavezan). Ali time sto ne radis LT i FT nista ne gubis jer ako ti kao izborni predmet uzmes procesiranje video signala (MPEG itd...) onda tu ucis FT. Takodje ako izaberes "advanced algorithms" onda ucis ozbiljnije o npr. linearnom programiranju, ako uzmes advance information systems ucis jos nesto itd....

Naravno ako izaberes da budes electrial & electronic engineer onda ti je ucenje LT i FT obavezno ali ne ucis neke druge stvari. A i to sto ucis, vise ucis kako da koristis nego da izvodis. Uci se izvodjenje ali jako uprosceno sa preskakanjem detalja - ali ti jasno naznace sta su preskocili tako da mozes sam da to potrazis ako te zanima.

Zato uglavnom fakulteti u inostranstvu koji su slicni ETF-u traju 4 godine a kod nas 5. (Mada cuo sam da je to kod nas promenjeno, mada me zanima kako su to izveli).

Ako upises CS onda ucis malo vise matematike - slicno pmf-u.

Knjiga od Tosica za matematiku 3 mi se svidja jer se lako cita i brzo shvata. Naravno ako nekoga vise zanima matematika onda mu verovatno Tosic ne moze preneti znanje (pogotovo ako je tacno to sto kazes) ali za ono sto je meni tada bilo dovoljno je sasvim ok. Da me zanima nesto vise verovatno bih pre diskutovao sa Merkleom a najpre sa tobom.

Ja se Srki u potpunosti slažem sa tobom oko toga da inženjeri treba da uče Matematiku i Fiziku upravo onako kako si opisao. To sam znao i ranije o pristupu na dobrim univerzitetima u razvijenom svetu. Međutim, to nije bilo primeljivo na ETF upravo zato što ljudi kao što je Dobrilo Dj. Tošić zahtevaju da na tom fakultetu predaju Matematiku samo oni koji su završili ETF. Posledica toga je da diplomirani elektroinženjeri treba da budu ujedno i diplomirani matematičari (videti moj prethodni post), a to studente dodatno opterećuje i ometa u sticanju inženjerskih skilova. E, zato Matematiku treba da predaju matematičari, a ne da Tošić i njegovi istomišljenici teraju studente tehnike da budu ujedno i matematičari, samo da bi odatle mogao da regrutuje svoje buduće asistente.

Postoji još jedna bitna razlika između našeg i zapadnog sistema visokog obrazovanja. Kod nas su skoro svi predmeti obavezni, osim jednog koji je izboran, a zapadni sistem podrazumeva manji broj obaveznih predmeta (osnova) i veći broj izbornih predmeta. To je malo bolji način sprečavanja nečijeg iživljavanja od izvlačenja cedulja, a time se poštuje i specifičnost svakog čoveka ponaosob.

Nedeljko, nemam sta da kazem osim da se slazem sa tobom. Ostar odgovor nisam mogao da ti dam jer nisam toliko tvrdoglav da dozvolim sebi da sam uvek u pravu. Ono sto je predlagao Tosic je mozda bolje, mada sada vidim da i nije nesto bolje (osim onoga da profesori sa etf-a izvlace cedulje, ovde profesori cesto predaju razlicite predmete) ali ipak je najbolje ono sto si ti rekao, da predaju matematicari po programu koji smisle inzenjeri. Sada mozemo da se vratimo na temu, dovoljno smo bili OT (mojom krivicom)

Samo da napomenem da ETF nije usamljen. Isti problem ima i Matematički Fakultet. Tamo glavnu reč vode matematičari koji ne odustaju od toga da onaj ko završi smer za Računarstvo treba da bude diplomirani MATEMATIČAR za Računarstvo i Informatiku. To upravo znači da oni takođe moraju da uče mnogo štošta što nema veze sa programerskom praksom (mnogo više nego na ETF-u). E, zbog toga je za taj fakultet interesovanje sve manje i bolji programeri izlaze sa ETF-a, jer ovi od tolike Matematike nemaju kad da uče programiranje.

Devedesetih godina sam znao za ljude koji su završili Računarstvo na Matematičkom Fakultetu za 4 godine sa prosečnom ocenom 10.00 i koji posle u praksi nisu znali ni da beknu. Kasnije su se stvari promenile na bilje, tako da sam sreo jednu devojku koja je skoro završila pomenuti smer na tom fakultetu i koja mi je pokazivala svoje seminarske radove iz Jave, Numeričkih Metoda, radila je i 3D grafiku (OpenGL) za Linux itd. Znači, danas se više pažnje polaže na praktični rad, ali bi trebalo taj smer još reformisati u istom pravcu. Međutim, smetnja je ono "matematičar" u nazivu zvanja.

Kada se matematičarima koji rade tamo pomene "kresanje" nekih matematičkih sadržaja, oni se nakostreše "Zamisli da oni ne rade teoremu Lebeg-Radon-Nykodima ili Rieszovu teoremu o reprezentaciji mere", pri čemu to nije našlo nikakvu primenu u Računarstvu. Zbog toga Matematički Fakultet propada (videti kraj prvog pasusa). Tamošnji matematičari jednostavno seku granu na kojoj sede.

Nego Srki, šta ti je to OT iz prethodnog posta.

Pa OT su desetak poslednjih postova jer tema je "sta je matematika", a ja sam krenuo da pricam o matematici na etf-u pa se tako produzila diskusija u tom smeru, a mozda mnoge to ne zanima. Ali ajde kada smo vec otisli u OT nema veze, nije strasno jer jos uvek pricamo o matematici :)

Sto se tice PMF-a i tvoje price, upravo sam tvoju pricu video u mom profesoru informatike iz srednje skole koji je predavao c a zavrsio je PMF. On je super znao to sto je predavao ali je predavao cist c, znao je super ono sto predaje a to su standardne funkcije i to je to. Nije znao neke advance stvari koje ti trebaju da bi to mogao prakticno da koristis. Ali on je takodje predavao prolog (koji je naucio na pmf-u) i to je nenormalno kako je dobro znao da resava zadatke u njemu. Dosta je zato trazio ali cesto kada i ja smislim neki zadatak on zaista nadje genijalno resenje. A zna se da ti za Prolog treba mnogo vise razmisljanja nego za proceduralne jezike. Tacno se videlo da je sa PMF-a. Ume matematicki da razmislja, ima super logiku itd.. Ali zato je razbijao prolog koji ti ne koristi mnogo u praksi (osim u specificnim situacijama) a ce je znao dobro ali samo osnove. Nismo ucili rad sa grafikom ili tako nesto jer se to verovatno nije ni radilo kada je on ucio PMF. Tada kada je on zavrsio se na pmf-u verovatno radio taj standardni c a c se koristio samo na unixima.

Iako si ti Srki, verovatno odavno na drugom kraju planete, verovatno se sećaš Fakulteta Organizacionih Nauka (FON). Oni su u prvoj polovini devedesetih uveli smer za Računarstvo i u međuvremenu im je priznata matičnost za oblast Računarstvo i Informatika. To znači da onaj ko završi tj. smer za Računarstvo na FON-u ima pravo da na bilo kom fakultetu bude biran za asistenta-pripravnika iz bilo kakvog programiranja, kao i da FON ima pravo daizdaje magistarske i doktorske titule iz oblasti Računarstva.

Budući da je FON matičan za Računarstvo koje je jedna od oblasti tehnike, sa punim pravom može sebe da naziva tehničkim fakultetom. Štaviše, još pre nekoliko godina su se profesori sa ETF-a žalili da više nemaju prestiž među tehničkim fakultetima, jer je na prijemnom ispitu najveća navala na FON, i zato što FON upisuje najbolje studente. To znam otuda što je jedan moj drug pre neku godinu radio na ETF-u (vrlo kratko, samo 4 meseca) kao honorarni asistent iz Matematike.

Dakle, trenutno je FON najelitniji tehnički fakultet u zemlji! No, to nije nikakvo čudo, jer je pored ludaka sa ETF-a i MATF-a trebalo samo da se pojavi neko normalan, pa da najbolje računardžije odu tamo.

Ma tek sam nesto vise od godinu dana ovde. A ja sam razmisljao da li da upisem FON i na kraju je prevagnuo ETF. Najbolji programer iz mog odeljenja je upisao FON i bio veoma zadovoljan i sada radi u inostranstvu. Reljam je zavrsio FON i sada radi u MS-u. Zaista sada dosta ljudi koji zele da se bave programiranjem upusije FON. Ako, to ce samo da natera ETF i PMF da malo lepse razdvoje smerove a ne da smerovi kao fora budu razdvojeni a prve 3 godine da ucis iste stvari. Evo cuo sam da od ove godine biras smer RTI od prve godine sto ranije nije bio slucaj. Ja duboko verujem da neko ko zavrsi RTI, a bude radio negde gde mu treba neka naprednija matematika ili poznavanje telekomunikacija, da to moze sam da nauci. Bolje to nego da sve teoretski znas a prakticno nista ne znas.

Nadam se da ce cela ova prica o pmf-u, etf-u i fon-u koristiti nekome.

FON elitni tehnicki fakultet! To nema veze sa ralnoscu! FON nikada nije bio, niti ce biti, tehnicki fakultet! To je nesto izmedju.

TMN: cini mi se da elitizam fakulteta odredjuje i profil studeanta koji ga upisiju, a jedno vreme je bila prava pomama, sto da neko uci matermatike ili elektrinike kada moze ekonomiju :).

Stvari se promenile, ovo je nova zemlja :)

FON je jedan od tri matična fakulteta za oblast računarstva. Ne znam kako vi, ali ja smatram Računarstvo oblašću tehnike. Danas najbolji programeri upisuju računarski smer ne FON-u. A informacija da je FON preoteo prestiž ETF-u na "tržištu" TEHNIČKIH fakulteta potiče iz "kuhinje" profesora ETF-a (pročitati moj prethodni post). Oni kažu da ne upisuju više najbolje programere, već da najbolji programeri upisuju FON. Doduše, ta informacija je stara dve-tri godine.

Imam drugara koji je u drugoj polovini devedesetih završio računarski smer na FON-u (kada je ETF bio najelitniji tehnički fakultet) i sada radi u Nemačkoj. Bavio se klasterizacijom, a sada rutira i lepo mu ide. Možda je nastava na ETF-u bolja. Ne znam. Ali znam da programeri koji otpadnu sa prijemnog na FON-u upisuju ETF. To kažu profesori ETF-a. Mnogo je veća navala na smer za Računarstvo na FON-u, nego na ETF-u. Nije to više samo "direktorski" fakultet.

Nego Srki, još nam ne objasni razne skraćenice kao što su OT i RTI. Ovo drugo je pretpostavljam Računaska Tehnika i Informatika.

Postovane Kolege:
1.) Racunarstvo je jedna zaista mala ablast Matematike.
2.) Tehnicki fakulteti obuhvataju daleko siru oblast od racunarstva. Ako pratim Vasu logiku, onda je Matematika tehnicke nauka! Me svi znamo da ona to nije. Racunarstvo i Matematika su alati neophodni u proucavanju tehnickih problema.

Sa postovanjem,

TMN

Racunarstvo je kao i fizika, nesto sto koristi znanja matematike (ne bas svi koji se bave racunarstvom, ali to je ionako nauka u povoju). Primenjena fizika jeste tehnicko znanje, kao i primenjeno racunarstvo.

TMN, kazem ti ja da se ovde puno toga promenilo u poslednjih nekoliko godina :).

Dakle, konvergirali smo ka pitanju iz opisa teme - šta je Matematika? Matematiku po mom dubokom ubeđenju od ostalih saznajnih delatnosti odvajaju njen metod i njen predmet proučavanja. Jedini metod zaključivanja koji se koristi u Matematici je dedukcija. Kakve god gluposti stajale u starim školskim udžbenicima Filosofije,


Dedukcija je metod zaključivanja kod koga je zaključak nužna posledica pretpostavki.


Narodnim jezikom rečeno, dedukcija je metod zaključivanja koji "ne može da omaši". Drugim rečima, to je metod zaključivanja kod koga nema nikakve mogućnosti da sve pretpostavke budu ispunjene, a zaključak ne, i to potpuno nezavisno od modela (interpretacije) pojmova iz formulacije. To je ujedno i opšti oblik svake matematičke teoreme: "Pod tim uslovima MORA da važi to". Često se u formulaciji teoreme ne navode sve potrebne pretpostavke, već se neke podrazumevaju, kao na primer u Geometriji geometrijske aksiome ili u Analizi aksiome polja realnih brojeva.

Mislio sam da ću svojim prethodnim postovima izbeći da odgovorim na pitanje iz naslova teme i samo dati ostalima relevantne činjenice za razmišljanje, ali eto, "vukli ste me za jezik", pa sad moram da se izjasnim. I druge discipline koriste deduktivan metod zaključivanja, ali ne kao jedini metod, već ga kombinuju sa drugim vrstama zaključivanja kao što je induktivno. Za Matematiku je karakteristično to da koristi dedukciju kao JEDINI metod dolaženja do saznanja.

Matematika, budući da koristi SAMO taj metod zaključivanja, pokušava da iz njega izvuče maksimum. Ona dakle proučava sve ono što se na taj način može proučavati. Nažalost, na taj način se može proučavati isključivo sama dedukcija, i to je jedini predmet proučavanja Matematike. Tako možete proceniti da i nešto pripada Matematici ili ne.

Dobar deo Teorijskog Računarstva je samo jedan deo Matematike. Međutim, ljudi ne uspevaju tu uvek sve da dokažu, već empirijski izvlače neke zaključke, i to onda više nije Matematika. Doduše, to i nisu baš nešto priznati rezulatati u Teorijskom Računarstvu, pa ono zapravo i jeste deo Matematike. Prvi na listi sedam matematičkih problema "ucenjenih" na po milion dolara je P prema NP, koji pripada Teorijskom Računarstvu.

Ipak, Računarstvo je nešto šire od Teorijskog Računarstva, tako da Računarstvo u celini nije deo Matematike, već je jedan deo Računarstva deo Matematike. Inače, postoji samo jedan razlog zbog kojeg Matematički Fakultet ne možete nazvati tehičkim: gospoda matematičari bi se uvredili. Čik da napišete na Matematičkom Fakultetu da je tehnički. Inače bi imali pravo budući da su matični za barem jednu oblast tehnike: Računarstvo.

Kraljica nauke (znanosti),
Arihmetika kraljica matematike Bel

"Arihmetika kraljica matematike Bel"
Zar nije Geometrija kraljica matematike!

A ja sam mislio da su Geometrija i Aritmetika oblasti Matematike. Ala sam bio u zabludi.

Šalu na stranu, ako pitate matematičara koja je najvažnija i najteža oblast Matematike, u najvećem broju slučajeva će to biti upravo ona oblast kojom se dotični bavi. Ovo je eksperimentalno provereno. Dakle, svaka oblast Matematike je za nekoga kraljica Matematike, i svaka nauka je za nekoga kraljica nauke.

Mada za mene je kraljica matematike logika, kojom se jesam bavio ali cisto onako da mi bude zanimljivo :).

U svakom slucaju, zanimljivo je da niko ne zna sta je to matematika a svi se bavimo njom :))).

Bas me zanima sta bi neko dete od 10 godina reklo da je matematika.

Zar Branko kockica i ja nismo ponudili odgovore?

Da da, Branko kocka u venu se bocka :).

Pa jeste, to je ono sto i boli :). Uzgred mislim da u recniku srpskog jezika pod odrednicom matematicar stoji: onaj ko dobro zna matematiku :), primer: Pera je u svom odeljenju najbolji matematicar :).

Eto, imamo najstariju nauku, bavimo se njom, a ne postoji nasa profesija :). I sto je najgore ne bi znali nikome da objasnimo cime se mi to bavimo :))).

Moze li ponovo jedno skretanje sa teme? :-)



Da li neko zna da mi objasni sta to tacno nije dozvoljeno u formulaciji Raselovog paradoksa? Zanima me posto sad u analizi1 stalno definisemo neke skupove i dokazujemo neke stvari preko njih, dok uopste ne ulazimo u to da li ti skupovi smeju da se definisu, a ocigledno postoje neki skupovi koji ne smeju. I sta uopste raditi sa problemima za koje ne znamo da li su dobro definisani? Pokazacu na primeru:

Profesor iz verovatnoce nam je prosle godine dao ovakav zadatak:
Dat je krug poluprecnika R. s je proizvoljna prava koja sece taj krug, i odseca tetivu duzine t . Kolika je verovatnoca da t bude vece od stranice jednakostranicnog trougla upisanog u dati krug?

Posle oko nedelju dana prosto je rekao da zadatak nije dobro definisan, ne objasnovsi zasto nije bio dobro def i kako smo mi to mogli unapred da znamo. Neka vrsta objasnjenja je bila da se dobiju razliciti rezultati kada se resava na razlicite nacine, ali to nikako ne mogu da prihvatim. Ne mozemo reci da problem nije dobro def zato sto do sada nije pronadjeno resenje ili zato sto se pri resavanju dobijaju kontradiktorni rezultati. Ako je problem ispravno definisan, a dobije se paradoks to znaci da aksiomatika nije dobra. Postoje li nacini da se sa sigurnoscu proveri da neka aksiomatika nije kontradiktorna?

I dalje ne znam sta ne valja u definiciji ovog problema, pa ako neko ima resenje i za to...

@devojcica
Pa ne valja to sto ne znamo na koji to proizvoljan nacin biramo tetivu. Ako neko izabere drugaciji nacin od tvog onda ce se i rezultat razlikovati.

@Nedeljko
OT je off topic. RTI je racunarska tehnika i informatika.

Poz.

devojčice:

raspravljali smo o ovom zadatku pre par meseci ovde. potraži, valjda u temama kao što su "najlepši zadaci" ili "najteži zadaci" ili nešto slično..

koliko se sećam, ima tri rešenja, u zavisnosti od načina "slučajnog" biranja prave, i to su valjda 1/2, 1/3 i još jedno valjda..

da znaš, i mene je pomalo začudio zadatak, tj rešenje, tj nepostojanje jedinstvenog rešenja.. jeste da nisam baš matematičar kao neki ovde, ali mi je tematika dovoljno bliska da razumem rešenje i implikacije istog.. ;)

u svakom slučaju, potraži, bila je dobra rasprava.. ;)

** Profesor iz verovatnoce nam je prosle godine dao ovakav zadatak:
Dat je krug poluprecnika R. s je proizvoljna prava koja sece taj krug, i odseca tetivu duzine t . Kolika je verovatnoca da t bude vece od stranice jednakostranicnog trougla upisanog u dati krug?**

Da nešto je bilo ovdje:

http://www.elitesecurity.org/tema/39907

U definiciji spornog skupa u Raselovom paradoksu ne valja to što se definicija tog skupa poziv upravo na skup koji se definiše. Ako ne znaš da li neki objekat postoji, a preko njega definišeš neki drugi objekat, onda ni za taj drugi ne možeš da tvrdiš da postoji. To je kao da si definisala funkciju f:R-->R sa f(x)= 7 za x<>3, odnosno f(x)=f(3)+2 za x=3. Postoje slu;ajevi kada su samoreferirajuće definicije korektne. U Teoriji Skupova postoji teorema rekurzije (nije ona iz Teorije Izračunljivosti) ili teorema o induktivnoj (ponekad rekurentnoj) definiciji. Te teoreme nam daju dovoljne uslove kada će takve definicije biti korektne. U opštem slučaju, kada imaš takvu definiciju treba da dokažeš da postoji tačno jedan objekat sa tom osobinom.

Nego Čupko, ja mislim da sam u jednom od prethodnih postova definisao Matematiku preko njenog predmeta proučavanja (dedukcija) i metode zaključivanja (dedukcija), pri čemu sam rekao i šta je to dedukcija. Dakle, Matematika je proučavanje deduktivne metode deduktivnom metodom.

Da, to je dosta dobra definicija naucne matematike, to definitno obuhvata sve oblasti matematike, ali sta cemo ako zagrabi i neke druge oblasti ?

Cisto da jednog dana istorija ne bude oblast matematike (mada cika Fomenko ...).

U tom slučaju, tvoj zahtev je preambiciozan. Niko danas ne može znati šta će naši potomci raditi u narednom veku.

Ja znam!
Naši potomci će u novom vijeku praviti naše potomke.

Sad su vec neke stvari jasnije... Hvala drustvo, super ste!

Moj mlađi brat ima 10 godina. Danas sam mu rekao: "Hajde da mi odgovoriš na jedno pitanje. Ima neki nagradni kviz na Internetu samo za malu decu i jedno od pitanja je šta je to matematika. Ako tačno odgovoriš, možda dobiješ neke lepu nagradu. Dakle, skoncentriši se i reci mi najbolje što možeš: Šta je to matematika?"

Dobio sam (čak i za mene) zaprepašćujući odgovor. Malo je razmislio, zažmurio napola kao da se nečeg priseća i reč po reč rekao: MATEMATIKA JE ZNANJE I UČENJE ZA PAMET.

He, he.

Matematika je nepokoriva činjenica,barem u našem svemiru.

Alal ti vera ako razumeš šta si napisao.

The math is beach!!!

Jel si ti isfrustriran matematikom? Pre bi trebalo da budes isfrustriran engleskim. Mislim da iz toga imas manju ocenu

očito mu engleski ne leži jer kad onu rič napiše kako netriba,nek se on ipak uvati matematike

Matematika je nepresušni izvor ideja,

Matemtika je sveopsta. Sve moze da se predstavi matematicki (skoro sve). A mozda ipak BAS sve....

Matematika je logicko promisljanje svojstveno ljudima tj. matematika je odraz zakonitosti koje vladaju u nasem umu.
Ovim sam hteo da kazem da putem matematika mi ljudi,kakvim nas je priroda stvorila sa nasim fizickim i umnim osobinama,nasim dozivljajem sveta,nacinom na koji funkcionise nase telo,cula,um i medjudejstvu coveka i prirode lakse razumemo i resavamo probleme.

Ovo prethodno, da ne citiram, je interesantno, human touch. Evo šta je meni došlo, reagujući na Nedeljkovu definiciju:

(Savremena) Matematika je nauka u kojoj se rezultati prikazuju isključivo deduktivno.

Proces dolaženja do saznanja je, ako hoćemo baš iskreno, nepoznat. Samom dedukcijom nikad ne bi nastala matematika, jer dedukcija polazi od gotovih pravila. A kako kada ona ne postoje? Priznaćete da je očigledno da sva ta pravila nekada nisu postojala (ajd' da kažemo da ih nismo bili svesni), pa iz čega onda dedukcija? Osim ako odbacimo evoluciju matematike :)

Na primer:
1. Nešto je intuitivno jasno; zadatak matematičara je da to potrvrdi koristeći dedukciju u nekoj od postojećih teorija (digresija: šta ako nema odgovarajuće? može nastati nova...); ovaj zadatak je u rasponu od trivijalnog do izuzetno komplikovanog.
2. Nešto deduktivno izvodimo; da li postoji intuicija ili ne u vezi zaključka je za samu matematiku irelevantno; ali zaključak je bolje usvojen ako je i intuitivno jasan, ako ga prihvatamo kao da je naš; postoje mesta na kome intuicija nema šta da traži, ili može doći tek mnogo kasnije.

Ja lično sam zadovoljan samo ako imam i deduktivnu i intuitivnu stranu. Ova intuitivna nije obavezno induktivna, ali to već zalazi u proces spoznaje koji za sada nije objašnjen, a možda i ne može biti. Sve u svemu, bio bih oprezniji u vezi "deduktivnosti" matematike. Samo postojanje mnoštva grana matematike pokazuje da se ona teško može na jedinstven način opisati. Takođe se shvatanja o pojmovima koje ona obrađuje značajno razlikuju, pa čak i validnost nekih tipova zaključivanja.

Matematika je verovatno nastala iz potrebe za nekom vrstom računa. Cenim da je proteklo mnogo vremena dok nije uočeno da se neki računi mogu podvesti pod isto i to je samo korak do apstraktnog računa. Ali danas i račun može značiti mnogo šta, npr. nalaženje primitivne funkcije, određivanje fundamentalne grupe ili utvrđivanje egzistencije rešenja. Ono što izdvaja matematiku od ostalih nauka je to što ne polazi od stvari iz našeg okruženja već od pojmova koje su proistekli iz mnogih apstrakcija i traganja za univerzalnim pravilima. I kao da postoji stara i nova matematika: prvo je bilo nagomilavanje pravila, odnosa, rešenja, a mnogo kasnije rekapitulacija i sređivanje.

Dedukcija nije metod prikazivanja, već dokazivanja (zaključivanja) koji se definiše kao onaj koji "ne može da omaši", to jest kod kojeg je izvedeni zaključak nužna posledica navedenih pretpostavki. Ne mora biti zasnovana na formalnim pravilima, a i o tim formalnim pravilima govori nezavisno od toga da li postoje bića koja ih znaju. To nije potrebno ni za kakvu diskusiju o njima.

Kad god se dese i A i B, onda se sigurno desi i A. Štaviše to je tačno bez obzira na našu svest o tome. Možda će neko reći da se time u suštini ništa ne tvrdi, to jest da je to svakako uvek tačno, ili da je posredi samo jezička zavrzlama, ali to je u suštini slučaj sa svim deduktivnim zaključivanjima. Problem je u tome što kod nekih deduktivnih zeključivanja nije lako utvrditi da su deduktivna. E, to je posao matematike.

Matematika se bavi dokazivanjem da su određena zaključivanja deduktivna. Jasno, to se ne može dokazivati "labavijim" metodama od deduktivnih, to jest samo je deduktivan metod dovoljno pouzdan za dokazivanje da je neko tvrđenje deduktivno.

No, ako je neko tvrđenje deduktivno, mi ga možemo dedukovati pozivanjem ne njega samog. To je trivijalan dokaz koji se sastoji od samo jednog koraka. Zaista, svaki korak tog dokaza je deduktivan, to jest dokaz ima deduktivnu snagu. Međutim, tu se odmah postavlja pitanje odakle mi znamo da je on zaista takav. Za to nem je bilo neophodno da znamo da je tvrđenje dato na početku deduktivno, a ako to znamo, onda nam dokaz njegove deduktivnosti nije bio ni potreban, tako da iako je formalno korektan, gubi svaki smisao.

Dakle, kada dokazujemo da je neko tvrđenje deduktivno, u dokazu koristimo neka druga deduktivna zaključivanja za koja već znamo da su deduktivna. Ali, pošto se to mora negde i završiti, neka tvrđenja neće biti dedukovana iz drugih, već prihvaćena bez dokaza kao "očigledna". No, o očiglednosti, kao i o aksiomatskoj metodi sam pisao ranije na ovom forumu.

Kada dva čoveka diskutuju o nečemu, da bi rasprava imala bilo kakvog smisla, moraju poći od stavova oko kojih se slažu, i na tim temeljima graditi diskusiju o onome o čemu se ne slažu. Ukoliko nekome nešto obrazlažete koristeći u argumentaciji stavove koje on ne prihvata, onda za takvog sagovornika ni takva argumentacija nije prihvatljiva. Zato se u dokazivanju, kod neaksiomatskog pristupa zaustavlja na što jednostavnijim stavovima (koji su što većem broju ljudi prihvatljivi), a kod aksiomatskog pristupa se za aksiome bira što manji broj što jednostavnijih tvrđenja.

Ja ne mogu da tvrdim da ne postoje i druge inteligentne vrste (zemaljskog ili vanzemaljskog porekla), koje nemaju svoju matematiku. Deduktivne zakonitosti su univerzalne, i u tom smislu postoji samo jedna matematika, koja je nama samo delimično poznata i koju doživljavamo i izlažemo na nama svojstven način, i ti je jedino po čemu se mogu razlikovati naša i njihova matematika. Druga inteligentna bića mogu znati druge delove matematike od nas i to svoje znanje mogu doživljavati i izlagati na njima svojstven način.

Kriterijum zaustavljanja u procesu dokazivanja kod neaksiomatskog pristupa, kao i kriterijum biranja aksioma je odraz našeg uma i naše intuicije. Inače, vrlo jaka intuicija je bila neophodna za dokazivanje bilo koje dobre matematičke teoreme. Kod automatskog dokazivanja teorema računari u suštini samo rešavaju neke kombinatorne probleme na koje su prethodno svedeni problemi iz neke klase matematičkih problema, a za to svođenje je bila neophodna jaka intuicija. Do doga su došli ljudi. To nisu mogli da urade računari.

Ovo sve što pišem važi samo za savremenu matematiku. Takođe, je ne mogu predvideti šta će matematika bidi za 200 godina. Naravno, da matematika nije bila uvek ovakva i da je postojao proces njenog razvoja koji se stiglo do ovog njenog oblika. To je proces usavršavanja našeg shvatanja matematike koji nije završen. Istinu govoreći, konačan odgovor na pitanje iz naziva teme ne postoji. Ovo sve se odnosi samo na trenutnu sliku matematike.

Matematika najverovatnije jeste nastala najre iz neke potrebe za računom, ali pošto se naše shvatanje matematike razvija, ona nije ostala samo na računu, čak i kada se on shvati u mnogo opštijoj formi. Nekada smo prevazišli okvire računa, koje smo takođe prethodno proširili, ali još uvek nismo prešli granice dedukcije, tako da ti okviri karakterišu današnju matematiku. Proces razvoja bilo koje nauke je praćen stalnim otkrivanjem novih zakonitosti i kasnijim uopštavanjem i objedinjavanjem istih. To nije karakteristično samo za matematiku.

Sve je to ok, slažem se. Ali ja sam mislio na sam taj proces dolaženja do zaključaka. Možda ja malo slobodnije koristim neke izraze, ali sam spreman da obrazložim takvo viđenje.

U bilo kakvoj teorijskoj nauci malo je nezahvalno reći kakve se metoda koriste, jer se većina procesa dešava u mozgu koji je teško opisati. Dakle, ja stavljam naglasak na činjenicu da jedino u šta smo sigurni u matematici, jeste to da zahtevamo dokaz za rezultat koji smo dobili, u smislu da ga možemo deuktivno izvesti u okviru neke postojeće teorije. I na to sam mislio kada sam rekao da se rezultati prikazuju deduktivno.

Razlog što to činimo tako jeste sve ono što si napisao u prethodnom post-u, ali ja se ograničavam da kažem da je metod dolaženja do zaključaka deduktivan u onom "radnom" smislu. Zapravo, čini se da se osvrnemo na dedukciju samo kada želimo da proverimo intuiciju; ili kada se zagubimo, ili želimo da proverimo da nismo previše odlutali.

Možemo da napravimo i malu anketu:
eto ja kažem za sebe da kada rešavam zadatak jako retko koristim dedukciju, već pre pokušavam da "osetim" problem i rešenje. Kada imam dovoljno ubeđenje da sam u pravu, pokušavam da izvedem dokaz. Usput možda ulepšam stvar ili dve, i na kraju se potrudim da sve zapišem precizno i u duhu onoga što sam prihvatio kao stil, za vreme studiranja.

Da li neko odmah reši zadatak koristeći čistu dedukciju? Blago njemu, jer to znači da ne mora da se zamara prevođenjem intuicije. Ne kažem da je nemoguće, ali meni se to dešava zanemarljivo malo puta.

Matematika je nauka nastala uočavanjem nekih zakonitosti u
u prirodi,a nakon toga se usavršava izučavanjem same sebe.

A koje to neteorijske nauke postoje?



Postoji podela metoda dolaženja do saznanja (napravljena je u filosofiji), i zna se gde je tu mesto metodama zaključivanja koje se koriste u matematici. Mislim da mešaš deduktivan metod sa aksiomatskim metodom. Osim one definicije dedukcije koju sam više puta naveo postoji još jedna njoj ekvivalentna. Deduktivan je onaj metod zaključivanja koji je valjan pri svim mogućim interpretacijama pojmova koji u njemu učestvuju. Jasno je da je neka argumentacija u matematici opravdana ako i samo ako ima deduktivnu snagu.

Dakle, matematički dokaz je neki niz zaključivanja, pri čemu je svaki korak deduktivan. To je dokaz koji je u matematici jedino prihvatljiv. Druga je stvar kako se dolazi do njega. Da bi se došlo do rešenja ozbiljnog matematičkog problema, potrebna je vrlo jaka intuicija. Mislim da sam to više puta naglasio. No, intuicija nam pomaže da dođemo do dokaza teoreme, ali je sam dokaz rešenje problema.



Da, s tim što priroda danas nije predmet proučavanja matematike već fizike. Ipak, nekada se počelo porvo sa brojanjem, pa sa merenjem površina i zapremina itd. Danas matematika traži zaključivanja koja su deduktivna deduktivnim sredstvima.

Pa nije valjda da misliš da su sve nauke teorijske? Interesantno stanovište, priznajem, ali meni se čini ipak da postoje one koje baziraju svoje rezultate na eksperimentima ili prostim opažanjem prirode i društva i one koje to ne čine...


Pa o tome i pričam. Kako dolazimo do saznanja u matematici je valjda njena metoda dolaženja do saznanja.


To baš rekoh: mi dolazimo do rešenja na bog te pita koji način, ali zapisujemo rešenje u obliku dokaza, koji mora da zadovolji deduktivnost. To je jedino mesto, i nije dovoljan razlog da matematičku metodu nazovemo deduktivnom, jer je to samo prezentacija rezultata.

Da, mislim. Eksperimentalne nauke pokušavaju da objasne pojave koje spadaju u predmet njihovog izučavanja, to jest da ponude teorijske okvire za te pojave, pri čemu se od teorija zahteva da se uklope u sve dotadašnje eksperimente i da ih objasne. Od teorija koje sa podjednakom tačnošću opisuju ishode do tada izvršenih eksperimenata boljom se smatra ona koja je jednostavnija.

smartam da su teske matematicke operacije potpuno nepotrebne
Buduci da je i AJNSTAJN imao 1 iz matematike a danas je poznat kao najfascinantniji fizicar svih vremena

Ne znam koja je jedinica usvojena za merenje težine matematičkih operacija, ali sve su uvođene sa nekom motivacijom. Inače, u Nemačkoj je manja ocena bolja od veće (1 je najbolja).

Ovo ti je sad malo konfuzno: u objašnjenju da je nauka teorijska, ti je nazivaš ekperimentalnom. Jasno je da svaka nauka pokušava da ustanovi neke zakonitosti, ali ako je njen izvor, pa i dokaz, posmatranje okoline, onda se istim pravom može nazvati i eksperimentalnom, kao što si i ti to učinio. Dakle, eventualno možemo reći da svaka nauka sadrži i teorijski deo. Ali ako joj dajemo jedan pridev, onda je to onaj koji je isključivo ili u većem delu karakteriše.

U tom smislu je jasno na šta se misli kad se kaže da je neka nauka teorijska. Ako hoćeš preciznije, matematika je isključivo teorijska nauka, jer niti dobija saznanja iz posmatranja niti ih proverava na takav način. Kontradiktorno, s' druge strane, izuzetno je praktična i možda najviše upotrebljena. Upravo iz tog razloga što se bavi računom. Nije ni čudo da su se do skora svi koji su doprinosili matematici uglavnom bavili još nekom naukom, iz koje su crpeli inspiraciju, zapravo nailazili na pitanja računa koji još nije bio rešen.

Dakle, matematici je okolina inspiracija, ali ne polazna osnova. Da nismo izučavali sam račun, matematika bi ostala na skupu pravila za računanje. Ali upotrebna svrha je ostala ista. Naravno, u poslednje vreme bavi se nečim što je daleko prevazišlo tu svrhu (mada račun ostaje kao važan deo svake teroije). I tu ima izuzetno interesantnih zaključaka, nekada iznenađujućih, kontra-intuitivnih. Ali zalazeći tako daleko u apstrakciju, ne mislim da saznajemo više o ustrojstvu prirode, već pre o sebi samima ili, još banalnije, o našem računu! Veću šansu imaju oni delovi matematike koji se bave nečim konkretnim.

U dedukciji je značaj na pronalaženju tih opštih pravila iz kojih ćemo kasnije ići ka pojedinačnom. Inače dedukcija vodi umrtvljavanju. Osim ako ne nađemo nešto toliko univerzalno i istovemeno kreaciono što će roditi sve ostalo. (Vernici bi rekli da je to Bog, a fizičari tragaju za svojom ujedinujućom teorijom.)
A kako dolazimo do tih opštih pravila je već drugo pitanje. Tu ima i redukcije i apstrakcije i ko zna šta sve ne.

Još jednom, ono što želim da istaknem je to da matematika, kalkulišući sa samim apstrakcijama, bitiše uglavnom u mozgu i zato je teško reći kako to sve zajedno funkcioniše.

P.S. Kako si ostao tako miran na očiglednu provokaciju? Svaka čast :)

Nauka je pokušaj da se nešto objasni. Eksperiment može biti sredstvo za ostvarenje tog cilja, ali suština je svakako u onome što je cilj, a ne u onome što je sredstvo za ostvarenje tog cilja. Čuo sam za podelu nauka na eksperimentalne (sve sem matematike) i ostale (matematika) prema tome da li koriste eksperiment kao metod ili ne. Međutim, za podelu na teorijske i neteorijske nisam čuo, pa ako već uvodiš nove pojmove, red bi bio da ih i definišeš. Ja nisam dokazivao da je neka nauka teorijska jer nisam ni čuo za takvu podelu, pa pošto ne znam na šta se odnosi, ne mogu ni da klasifikujem nauke prema njoj.



Meni nije jasno. Objasni mi. Takođe, matematika ne mora da crpi inspiraciju iz okoline. A da se matematika bavila samo (ili pretežno) konkretnim stvarima, nikada ne bi postala ovo što je danas - ubedjivo najprimenljivija ljudska delatnost bez ikakve konkurencije. Štos je upravo u tome da su deduktivni plodovi tačni u svim interpretacijama pojmova na koje se odnose, što im i daje toliku širinu mogućnosti primene.

Ovo sa umrtvljavanjem uopšte ne razumem. Za mene je matematika daleko lepša i bogatija od svih njenih primena. Ipak, pod matematikom podrazumevam njenu suštinu, a ne naš doživljaj nje, ili naše saznanje o njoj. Sva ta pravila su mnogo starija od nas i od našeg saznanja o njima. Smatram da se matematika ne izmišlja, već otkriva, a da se izmišljaju samo načini njenog izlaganja, njen doživljaj i načini da se ona razume.

Evo, vratio sam se nekoliko post-ova unazad da kažem konkretno na šta sam reagovao, da se ne bi rasplinuli:

Dakle, ono što ja hoću da kažem jeste da je to jedini način da ZAPIŠEMO rešenje u okviru matematike, ali da nikako nije metod, a ponajmanje jedini, dolaženja do saznanja.


Ja sam (malo) manje formalan i nisam ni znao da postoji podela na eksperimentalne i one koje to nisu. Ali, eto, recimo, čuo sam za teorijsku fiziku, pa me sad zanima da li je to ostala (neeksperimentalna) nauka ili eksperimentalna?

Pođimo od jezičke komplementarnosti pojmova: teorija i praksa. Dakle, nauka koja nema praktični deo (a on može da se odnosi na eksperiment ili slično, ali se u svakom slučaju odnosi na manipulaciju/posmatranje naše okoline) je teorijska. Ili, prostije rečeno, ona za koju je dovoljna olovka i papir.

Što se tiče primenljivosti, to sam isto i ja rekao u prethodnom post-u, pa mi se čini kao da ih ne čitaš baš najpažljivije, samim tim što si toliko to istakao. Pardoniram ako grešim :)

A opet bih da postavim pitanje: ako je dedukcija jedina, a potrebne su joj pretpostavke, ko pravi pretpostavke? Pa valjda su i te pretpostavke sastavni deo matematike? Zato kažem da dedukcija umrtvljava, jer kad već dođemo do pravih pretpostavki, ostalo je samo rutina, nužnost. Pošto ne može da ih rodi, a bez njih je matematika slepa, dedukciji ostaje da bude samo dobar saobraćajac, koji će reći gde smemo gde ne, da li je ulica jednosmerna ili ne i slično. I koliko puta se dešava da, želeći odgovarajući zaključak, menjamo pretpostavke, jer se pokazalo da nisu dovoljne. Dakle, kao da je to igra u kojoj se i rađa matematika.

Naravno, može se reći: pa dobro, to su neke pretpostavke, dajte druge, pa ćete dobiti nešto drugo. Ali to je slab izgovor, jer relativizovanje pretpostavki (najvećom verovatnoćom) dovodi do neupotrebljivosti teorije. Jasno je da matematiku imamo jer smo imali neki cilj gradeći je. Dedukcija je (dobar) izgovor da je smatramo pravilnom.

Oko ovoga već ne možemo raspravljati. Tu se radi o standardnim pojmovima koji imaju standardne definicije. U tom slučaju se jednostavno konsultuje neki udžbenik filosofije, deo koji obrađuje metode (načine) zaključivanja (dolaženja do saznanja), pogleda se u klasifikaciju i pročitaju se definicije navedenih metoda dolaženja do saznanja. Dedukcija je metod zaključivanja, a ne zapisivanja.

Teorijska fizika i eksperimentalna fizika nisu nauke. Nauka mora da ima predmet izičavanja i metod. Nauka je u ovom slučaju fizika, a ona ima svojun metodologiju koja obuhvata eksperimentalni deo (prikupljanje činjenica) i teorijski deo (nalaženje što jednostavnije teorije koja se uklapa u do tada prikupljenu ekspeimentalnu građu). Za prvo nisu dovoljni olovka i papir, a za drugo jesu, mada se nijedan od tih delova ne može u celini obuhvatiti matematički. Razlog leži u činjenicama da se eksperiment u fizici ne bi ni koristio kada ne bi bio neophodan, kao i da pojam jednostavnosti nije matematički. No, ovo ipak ostavlja nadu da postoje nauke osim matematike za koje su dovoljni olovka i papir.

Primer deduktivnog zaključivanja je: Ako važe A i B, onda svakako važi i A. Tu su A i B pretpostavke, dok je zaključak A. Zaključak je zaista nužna posledica pretpostavki. Pritom, te pretpostavke nisu ni prave ni krive, već jednostavno uslovi od kojima izvedeni zaključak mora da važi.Svaka matematička teorema ima pretpostavke i zaključak. Matematici pripada zapravo ta uzročno-posledična veza koja važi pri bilo kakvoj interpretaciji polaznih pojmova na koje se odnosi. Ukoliko pretpostavke nisu dovoljne za izvođenje zaključka, onda takvo tvrđenje nije deduktivno, to jest nije matematička teorema, pa onda svakako nešto treba menjati, ili pretpostavke ili zaključak.

Stvarno? To zaista nisam znao. Dakle ako se neko bavi nekom od ovih (kako sad to da nazovem) disciplina, onda on nije naučnik? Interesantno. A šta one nemaju od ova dva: predmet ili metodu?

A eto i filosofija koju pominješ, da li je ona nauka? I ako jeste da li je eksperimentalna ili ona druga, gde si rekao da spada samo matematika? Ako nije, zašto bi se obazirali na njene zaključke, ko garantuje za njih?

Moraću da ponovim svoje pitanje, jer izgleda da propuštaš (drugi put) da odgovoriš na to:

Dakle, da bi izveli zaključke i uopšte došli do toga da nam treba neka metoda zaključivanja, potrebne su nam pretpostavke. Ako je dedukcija jedini metod dolaženja do saznanja, kako saznajemo pretpostavke?


Ili ja pričam kineski ili ovde neko nekog... Ja napišem nešto, a onda mi ti u odgovoru napišeš to isto, ali bez onog smisla koji sam ja želeo da istaknem. Eto, ovde je pitanje npr. na osnovu čega ćemo odlučiti da li da dodamo pretpostavku ili da promenimo zaključak? Možda zvuči banalno, ali ja mislim da je to veoma važno pitanje jer takve stvari uobličavaju matematiku!

Ako se neko bavi teorijskom ili eksperimentalnom fizikom, on jeste naučnik, i to fizičar. Može se čak reći i da je on teorijski ili eksperimentalni fizičar ne bi li se precizirala njegova delatnost na polju fizike.

Neke od oblasti fizike (ili fizičkih disciplina) su na primer opšta teorija relativnosti, teorija kvantovanih polja, mehanika fluida itd. Ne postoji oblast fizike koja se zove teorijska, odnosno eksperimentalna fizika. Proces dolaženja do saznanja u fizici se može podeliti na teorijski i eksperimentalni deo. Dakle, to nisu fizičke discipline, već delovi procesa dolaženja do saznanja u fizici. Svaka od oblasti fizike ima teorijski i eksperimentalni deo. To je kao da imaš jedan skup F (fizika) koji se može predstaviti kao manje-više disjunktna unija skupova O₁,...,O_n (njene oblasti), pri čemu se isti taj skup F može predstaviti i kao unija dva disjunktna skupa T (teorijski deo) i E (eksperimentalni deo), od kojih svaki seče svaki od skupova O_i. Dakle, niti skup T, niti skup E se ne poklapa niti sa jednim od skupova O_i.



Pretpostavke se ne saznaju, već biraju tako da obezbede važenje zaključka, i tako da po mogućstvu da ta veza bude što netrivijalnija. O njihovoj istinosnoj vrednosti ima smisla govoriti tek pri nekoj interpretaciji polaznih pojmova na koje se to tvrđenje u celini odnosi.



Bez ljutnje, molim! Konkretno, napisao si



To sam protumačio kao da hoćeš da kažeš da to protivreči nekim mojim stavovima, mada nisam razumeo kojim i na koji način niti šta si time hteo da kažeš. To je kao kada strelac gađa metu pa ponekad promaši. Isto i u matematici. Pokušavamo da pronađemo nužnu vezu, pa ne uspemo, pa onda nešto popravljamo. U svakom slučaju, dok ne okrpimo tvrđenje i dokaz nismo došli do matematičkog rezultata.

Matematika je najveca glupost na svetu zato i imam 2 iz matematike dok iz fizike imam jedini 5 u razredu
ZATO nemojte da lupate glavu teskim matematickim operacijama , bolje da igrate fudbal

Ajd' da batalimo ovo van glavnog, nemam više motiva da raspravljam o tome šta jeste a šta nije nauka; rekao si da nemaju metodu i/ili predmet, a sad nešto drugo. Razumem ja to ali ne razumem zašto sad drugačije objašnjenje; očekivao sam, naivno, da ćeš reći šta koja od pomenute dve nema.


Pa to je samo pitanje jezika. Ako ja prvo nisam znao koje mi trebaju pretpostavke, a kasnije znam, onda sam je valjda nešto saznao? Ti pričaš kao da sve već postoji, samo treba izabrati? Pa zato i kažem da dedukcija ne vodi napretku. Odgovori mi sad na ovo: a šta ako nemamo odakle da izaberemo, kao što se mnogo puta dešavalo u istoriji matematike?

Dakle, što se mene tiče, matematika ne samo da ne bi bila ovakva kakva jeste, već ne bi bila uopšte da smo se držali samo dedukcije.

Ajd' sad ovako: recimo da je potrebno napraviti teoriju koja opisuje neki nama bitan račun ili štagod. Dakle, potrebno je doći do saznanja koje su osnovne karakteristike i napraviti izbor osnovnih tvrđenja tj. aksioma. Reci mi sad, kako bi smo saznali to koristeći samo dedukciju?


Začuđuješ me. Ako zaista ne razumeš šta pričam, a polako mi to izgleda sve verovatnije, onda se džaba i trudim. Pričaš o pokušaju i promašaju kao o nečemo što radimo u matematici, a to ne prihvataš kao metodu? Ili je i to dedukcija? Metoda je svaki konkretan trud koji činimo da bi došli do saznanja. Ovo recimo kod tebe nije uvršteno.

Ako se neće naljutiti Darko i Nedeljko ja ću se umiješati.
Ode ovo vaše u filozofiju.A fizika i matematika su se odgranale
od filozofije jer je pored deduktivnog i intuitivnog spoznavanja
uticajan postao i induktivni.
-U fizici,opažanje uzroka i posljedice,pa onda variranje uzroka
i tabelarni prikaz posljedice.Nužno traži se mat. opis i to vodi
razvoju matematike koja to apstrahuje do krajnjih granica.
Pa onda tako apstraktne teorije odjednom se pojave kao
korisna alatka u opisivanju sasvim novih fizičkih zakonitosti.
Ima grana matematike koji ne vuku korijen iz fizike,i u samom
početku nisu imale praktični smisao.(naprimjer logaritam)
Ali kasnije su došle do izražaja jer im je nađena primjena i
u realnosti i u razvoju matematike.
---------------------------------
Aristotel je deduktivno izveo nekoliko zakona koje je bez
indukcije teško bilo oboriti.To je ono:horizontalni hitac
opisuje kružni luk;teški kamen brže pada od lakog..
---------------------------------
Tiho je opisao kako se vremenski mijenja položaj planeta.
Kepler je iz tog izračunao neku zakonitost.Ovisnost ploha
i vremena,i udaljenosti i vremena obilaska oko sunca.
---------------------------------
Njutn je to obadvoje opisao matematičkim zakonom.
----------------------------------------
Ako treba baš da se izjasnim onda navijam za Darka,jer
bez intuicije nema napretka.Mora biti i dedukcije da to
uveže,ali bogami bez indukcije nema ništa.

zzzz, nemamo mi šta da se ljutimo, ovo je mesto na kome svako ima pravo da iznese mišljenje (pa i ti) u skladu sa pravilnikom. Kome se to ne sviđa, taj ne treba ni da posećuje ovaj sajt. Dakle, sve je u redu.

Darko, nadam se da se slažemo oko toga da niko od nas nije zlonameran, ali da postoje određeni problemi u komunikaciji, što je i prirodno budući da se niti jedna misao ne može iskazati. Ipak, ja primećujem napredak u našem međusobnom razumevanju, te stoga vidim svrhu ove naše diskusije.
Meni si ti nakon tvoje poslednje poruke jasniji nego što si bio pre nje.

Metod koji se koristi u nauci je zapravo dogovoreni skup pravila igre. U šahu se tačno znaju pravila igre, a na igraču je da pobedi protivnika na bilo koji način koji je po pravilima te igre. U matematici je dozvoljeno koristiti bilo koje pravilo kod kojeg je zaključak nužna posledica pretpostavki. Pravilo kod koga to nije slučaj, u matematici nije dozvoljeno primeniti.

Ali kao što u šahu nije dovoljno poznavati pravila da bise pobedilo, tako i matematika, baš kao i šah, zahteva intuiciju i kreativnost prilikom dolaženja do novih rezultata. Da li smo se sada makar malo bolje razumeli?

@Nedeljko
Šta reći, sem: huh! Konačno! :)

Naravno da nema zlonamernosti, ali si uglavnom previše formalan, i to koči komunikaciju. Al' ajd' sad. Dakle, mislim da je jasnije zašto sam insistirao na dedukciji kao načinu da zapišemo rešenje, aludirajući na to da mi vršimo svakojake radnje da bi došli do rešenja, ali da smo dužni da na kraju to napišemo kao da smo izvodili deduktivno. Takav način krije mnogo toga i to više što je tema apstraktnija. Mislim da, generalno, takav način ubija intuiciju, i, iako je neophodan, mnogo je lepše kad uz to ide pričica koja treba da nahrani istu. Misao se bolje prenosi, a, na kraju krajeva, iskrenije je. Pa nije nam valjda dokaz izašao baš takav kako ga zapisujemo?

I analogija sa šahom je dobra. Ja bih još dodao da pravila igra sama po sebi ne mogu dovesti do razvoja, ne samo do pobede. Zato sam govorio o umrtvljavanju, mada to možda zvuči prejako rečeno.

@zzzz
Hvala Milane na podršci, znao sam da mogu da računam na tebe, stari druže ;)
Što se tiče filosofije, verovatno si u pravu, ali filosofsko je i pitanje. A i ja sam prilično filosofski nastrojen, i eto...
I takođe mislim da je indukcija (ne matematička, već ona konačna) izvor svakojakih stvari u matematici. Rekao bih čak da je ugrađena u sam gen života, jer je neophodna za opstanak, pa čak i evoluciju (sad sam zaista otišao predaleko :) Nije ni čudo da i na ovom, apstraktnom, nivou predstavlja generator ideja.

"Matematika je jedna veoma prosta nauka, zavijena u sarenu oblandu onih koji je ne razumeju da bi izgledali veliki u ocima onih koji je (matematiku) ne znaju." Ovo rece jedan francuski matematicar.

matematika su brojke !?

Teorijska Fizika je fizika koja jos nije nasla primenu.
Matematika je najelegantnije koriscenje uma i prirode.Strasno je jednostavna,kada se za nju ZAINTERESUJETE.



Potpuno se slazem. :)

Sta je Matematika ???
- Matematika je sve ;)

Upravo to i ja mislim.Gde god se okrenes naci ces Matematiku.

Mozhda se mozhe i ovako sagledati na svijet:
tri su znanosti koje su neophode, ostalo stinks :> - matematika, fizika, kemija. Pomochu te tri znanstvene discipline, kompletni se svemir (prostor, vrijeme, materija, anti*, ...) mozhe definirati i uoblichiti u formu shvatljivu nama.

Sve ostalo je tu samo kako bi olakshalo ljudima shvachanje... pa, ukratko SVEGA (opet svemir - prostor, vrij...). Npr. biologija je zapravo kemija s izrazhenijim primjesama fizike i neshto malo matematike. Geografija je fizika s podosta kemije te prisutnom matematikom. I tako dalje, samo u razlichitim omjerima :>.

A shto bi bila matematika? Uoblicheno znanje o brojevima*!? Istazhivanje osobina brojeva*!? Definiranje brojeva* unutar nekih parametara!? ...

BTW, nadam se da chete oprostiti ako sam neshto napsiao shto je vech bilo. Nije mi se uopche chinilo kao pametna ideja chitati sve od pochetka.

<sub>* - laichki gledano (tek sam krenuo u srednju :>)

[Ovu poruku je menjao s!c dana 20.08.2005. u 22:45 GMT+1]</sub>

"Matematika moze da se definise kao predmet u kome mi nikad ne znamo o cemu govorimo, niti da li je tacno to sto govorimo."

Bertrand Russell. 1872�1970

Rasel je poznat po raznim glupostima, kao na primer da matematička knjiga ne može biti i korektna i čitljiva, koje samo pokazuju koliki je bio nnjegov stepen nerazumevanja matematike.

Ma čovek je samo upozoravao na nedostatke matematike.

Pa za to nije kredibilan neko ko matematiku ne razume.

Tolstoj je napisao niz knjiga i ceo svet zna za njega kao vrsnog književnika. Kod nas je Tasković u dva toma napisao "Nelinearna funkcionalna analiza" na 2000 strana. Da bi ste shvatili jednu stranicu te analize treba vam vremena koliko i za shvatanje jednog Tolstojevog romana. Za Taskovića malo ko zna van fakulteta. Ali Tolstoj je pisao o intrigama, lažima i prevarama.

Pročitao sam jednu zanimljivu knjižicu, autor je matematičar, gde je glavni zaključak da je upravo trač - pričanje o događajima koji se tiču drugi ljudi, uglavnom intrigantni, (evolutivni) razlog za nastajanje sposobnosti koji dovodi do "matematičkog uma". Praveći paralelu da su obe discipline (trač i matematika) apstraktne - pričaju o onima "koji nisu tu", i obe se bave nečim što nas lično ne dotiče. Tako da je možda Tolstoj mnogo bliže Taskoviću nego što se čini :)

Familijarizacija i poistovećivanje je potrebno u oba slučaja. Kada su ti matematički pojmovi dovoljno bliski, onda lakše pričaš o njima.
Možda je to razlog zbog kojeg Nedeljko misli da izjava "matematička knjiga ne može biti istovremeno korektna i čitljiva" vodi ka zaključku o nerazumevanju?

Za mene je Tolstoj običan davež i ništa više od toga.

Voli da raskopava, i nalazi cudno uzivanje u tome. Ne razlikuje banalno od lepog.

@Nedeljko
Pa to je zato što te to ne zanima :)

A ja nisam rekao da Nedeljko nije u pravu...
Moram priznati da mi je teško da osudim nekog ko em nije živ, em ne poznajem dovoljno njegov rad, ali pomenuto rasuđivanje mi nije nerazumno...
Odnosno, hoću reći, uklapa se u priču o familijarizaciji...

Moram da priznam da vas ne razumem, i da ne znam o cemu pricate. Izgleda da smo ipak dva razlicita, veoma udaljena sveta.

Ajmo ovako. Da li imate bilo kakve koristi od Tolstoja (osim ako ste bibliotekar ili izdavač - trgovac knjigama) ? S druge strane matematiku koristite svakodnevno.

Pa, imao sam koristi od Dostojevskog, tako što sam sa uživanjem čitao "Braću Karamazove".

Vrlo je cudno sto moram da izgovorim ovo. Ja se samo cudim nesto u zadnje vreme.

Knjige tih pisaca cine temelj ljudske civilizacije i humanizma. Sama svest covecanstva, prihvata i utvrdjuje te temelje i svoj put kroz njih. Nisi ni svestan koliko u svakodnevnom govoru koristis misli tih pisaca, misleci da postoje same od sebe. Tako da mnogo vise u svakodnevnom zivotu osecas prisustvo ideja tih pisaca, i ne znajuci ih koristis.

Neverovatno je koliko nepoznavanje pokazujete ovde. Reagujem samo da ne biste vodili na pogresan put mladje ljude.




Ovakvu aroganciju nikad nisam video. Za tebe su prevazidjeni, i Pitagora i Euklid, Bertrand Rasel je glup, nije kredibilan da govori o matematici, i ne razume matematiku, a o Tolstoju, jedino sto si imao da kazes, je da je davez. Sad ti je i Dostojevski za podsmeh, a citanje njegovih dela, obicna zabava.

Niste svesni svoje nesvesti.

Koji podsmeh? Šta lupetaš? Pa, normalno je da književnost čitam iz zabave. Nego zbog čega?

@boxxter
Hm, pa nisam rekao ni da je u pravu, nego samo da mi se logika čini razumnom... A što se tiče svetova, nemam pojma, ne poznajemo se.

Nisam siguran na koga se ovo odnosi, ili persiraš Nedeljku?

To što strasti i ratovi postoje vekovima pre i posle pisca nije piščeva zasluga što neki pojedinac prolazi kroz slična iskustva. Ne koristi niko ideje Tolstoja i Dostojevskog pogotovo ako nije ni čuo za njih. A ipak možda prolazi slična iskustva ali to nije zasluga pisaca.
Arhetipi ponašanja imaju veze sa civilizacijom ali same knjige tih pisaca sigurno ne.

Ako posmatramo Košija onda možemo reći da više od 50% ljudi uopšte ne može shvatiti ideje koje je on iznosio. Ipak u njegovim radovima nema prepričavanja šta je ko spletkario protiv koga. Radovi Košija su zaista originalni a Tolstoj i Dostojevski samo malo veštiji plagijatori.

@holononi
Malo previše insistiraš na tome kako velike matematičare većina ljudi ne razume. Ne znam šta je tu dobro? :)
A i što se tiče pisaca verujem da se njihov uticaj na civilizaciju ne može zanemariti. Kad reče "prepričavanja", čini mi se da onda ti spadaš u one koji ne razumeju npr. Dostojevskog, a izgleda da i takvih ima priličan broj procenata...

E sad što je za tebe lepše da shvatiš Košija, to je tvoja subjektivna perspektiva.
Moje je lično ubeđenje da bi se matematičke istine kad tad pojavile, bilo je toliko neverovatnih ljudi koji su se bavili matematikom, da teško da bi nešto promaklo. Posebno ne nešto što bi imalo veći uticaj na "civilizaciju". S druge strane, veliki pisci mi se čine unikatnijim i teško da bih mogao da zamislim da bi neko drugi napisao npr. Braću Karamazove.
Razlog možda leži u tome što su romani mnogo ličnije stvari nego što je to matematika, koja zapravo upravo suprotno pokušava da bude najopštija moguća.

Dakle, ove dve discipline streme različitim stvarima, pa ne znam ko želi to da poredi?
Ono što ih spaja je napisano u nekom od prethodnih mojih postova, ali izgleda da niko ne čita :)

Veruj mi da moja komšinica mnogo bolje tračari. Osim toga zrači optimizmom. Zašto bih se onda opterećivao izmoždenim likovima survanim u beznadje ludila. To je posao za psihijatre ne za mene.

Inače pominjanjem Košija nisam mislio na lepotu već upotrebljivost. Da je po Tolstoju ti bi pisao guščjim perom a za računar ne bi ni čuo.

Bez kulture ne bi pisao ničim. Kavi kompjuteri, kakva pera.

Nisu računari nastali iz želje za kulturom već iz potrebe da se broje ovce.

Nisu umetnici napravili atomsku bombu nego naučnici.

Onima koji ne shvataju značaj kulture za razvoj civilizacije, ne vredi objašnjavati.

Nakon što je zadenuo računar za pojas, programer je u debeloj ladovini zasvirao u frulu. Videvši ga da planduje naišla je komšinica ali pre romantike je morao da se nasluša tračeva. I tako je nastala kultura i umetnost.

Ta dela prozima duhovnost. I dosta je zrtvi podneto, da bi se pojavila na svetu. Ako ih citas iz zabave, podsmevas se autoru. Mada imas pravo na to. I da citas, i da ne citas, i da se podsmevas. I da se zabavljas. Covek uradi sta hoce.




S ovim se slazem. Pristojnost je osnov svega. Cudno je da neko uziva plodove necega sto ne priznaje. To je fenomen. Zbunjujuci fenomen. Cesto se srecem s tim.

Nadam se da necu nikoga uvrjediti svojim postom ipak ovde ima malo boljih od mene na sajtu a ja sam jos "zelen" ovde.

Sto se tice knjiga ja ih citam da bih vidio kako su ljudi zivjeli i naucio nesto.Dotakli smo se ruske knjizevnosti.(odlutah od teme ali...) Za mene je recimo djelo "Sinjel" od Gogolja odlicno.Govori o covjeku koji se odreko caja i dvopeka samo da bih kupio sinjel (kaput) i tako zivio (nesjecam se sad tacno) nekoliko mjeseci.
Pa ja zelim da postanem dobar programer i ucim to,trudim se ali i znam da ima dosta odricanja.Neizadjenih izlazaka,provoda,svega ali na kraju cu uspjeti da napravim neki sistem (sto mi je cilj) i instaliram ga na svoj komp.Znam koje mi treba znanje i to dobro.Eto recimo,meni je to jedan nacin da vidim da je sve moguce i da se moze kad se hoce.Ja citam knige da bih nesta naucio a zna se i fino zabaviti uz neka djela.

Sto se tice matisa.Neko moje misljenje je da je matematika sve.Osnovana nauka.Jer isto kao sto se u matematici ne moze definisati sta je tacka a eto od nje se polazi u neka dalja definisanja.Ili recimo sto se dva pise 2 a ne kao tri.Tako je matematika,za mene,osnova od koje se polazi u dalja definisanja i utvrdjivanja.

Mlad si, i nemoj da nasedas na price, i gluposti i lazi koje su izgovorene ovde. Zivot je kompleksan, i ne sastoji se od bezdusnih brojeva, nego i od tvojih emocija i duha. A nase postojanje zavisi od toga kako cemo da verifikujemo ljudsku podlost, pokvarenost i sujetu, tragajuci za slobodom, i to kroz izgovorenu rec, i napisanu rec, dobrog, mudrog pisca. Tu covek nadje i utehu. Tolko bednog je ovde izgovoreno, da je nemoguce dosegnuti dubinu besmislice.
Jos od Heraklita koji je ziveo 500 godina pre nove ere, koji je govorio da je pogresno zrtvovati ljude i zivotinje bogovima, i prolivati neduznu krv, matematika i nauka, i racionalni razum, jesu nerazdvojivi. Svet kakvog danas poznajes, nije bio takav. Mnogi su se zrtvovali da bi danas ovako izgledao. Poneko ce mozda i da postuje zrtve koje su polozili ljudi koji su postavili temelje civilizacije, mada oni to nikad i nisu trazili. Covek uvek uradi sta hoce.

Mnogo ucenja, ne uci nas razumevanju.

-Heraklit-


Matematika je jezik.

Gibbs, Josiah Willard. 1839-1903.

To da je matematika jezik razumijem isto kao i C/C++ jezik koji mora da zadovoljava neke uslove da bi nesto (program) bili tacni i razumljivi.
Citao sam neke postove na pocetku ove teme.Tesko je reci sta je to matematika.To samo mogu definisati filozofi,knjizevnici na njihov nacin a to sto oni kazu matematicari nece prihvatiti i tako u krug.

Matematika je harmonija.

-Ja. I Pitagora.- =) :D

najlepša i najkorisnija nauka na svetu!

služi da razgraniči pametne (koji je vole i poznaju) i glupe (koji je ne vole i ne poznaju)

U toj gradaciji "pametni" - "glupi" gde se nalaze oni koji:
- vole je i ne poznaju? ili oni
- ne vole ali je poznaju?

Pa, tada je kriterijum neodlučan.

Kad se matematika zvala račun, svi su znali šta je i čemu služi :)

Kad je to bilo?

pevanje - muzičko vaspitanje
fiskultura - fizičko vaspitanje
crtanje - likovno vaspitanje
...

Bilo nekad, kada su naši roditelji išli u školu ...

Jesi li siguran da se iz računa učila matematika?

Siguran sam.

Ja mislim da se učio samo račun.

Štaviše, u tzv. realkama (realna gimnazija) se radila matematika (aritmetika) i nacrtna geometrija, a negde i još geometrija.

_{[Ovu poruku je menjao mokelet dana 25.08.2010. u 02:40 GMT+1]}

Matematika je nauka o formalnim odnosima.