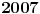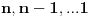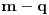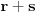[ cassey @ 11.09.2007. 11:39 ] @
|
[ Bojan Basic @ 11.09.2007. 12:23 ] @
[ Farenhajt @ 11.09.2007. 12:50 ] @
Za prvi bi očigledan motiv bio da se srce centralnosimetrično preslika u odnosu na P, i da se onda dokaže da se slika i original moraju presecati u dve tačke...
[ cassey @ 11.09.2007. 12:56 ] @
Citat: Bojan Basic: Evo na brzinu rešenja trećeg, a i ostala dva će doći na red. :) Odvojimo 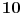 novčića na novu gomilu i sve ih okrenemo. novčića na novu gomilu i sve ih okrenemo.Jeste. A evo i malo uopstenje tog zadatka: pored navedenog uslova, gomile moraju da sadrze po 50 novcica. [ Bojan Basic @ 13.09.2007. 14:18 ] @
Evo rešenja drugog (mada mi nešto govori da sam ga malo iskomplikovao).
Za neparan broj  nazovimo serijom poteza okretanje najpre nazovimo serijom poteza okretanje najpre  , zatim , zatim  , onda , onda 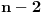 ... i na kraju jednog novčića. Dokazaćemo indukcijom da za svako neparno ... i na kraju jednog novčića. Dokazaćemo indukcijom da za svako neparno  postoji postavka takva da su svi novčići na istoj strani (dakle, sva pisma ili sve glave) i serija poteza koja od nje dovodi do proizvoljne, unapred zadate kombinacije. postoji postavka takva da su svi novčići na istoj strani (dakle, sva pisma ili sve glave) i serija poteza koja od nje dovodi do proizvoljne, unapred zadate kombinacije.Za  stvar je očigledna (novčić postavimo suprotno od onoga što nam treba, i prevrnemo u prvom i jedinom potezu). Pretpostavimo da važi za sve neparne brojeve do stvar je očigledna (novčić postavimo suprotno od onoga što nam treba, i prevrnemo u prvom i jedinom potezu). Pretpostavimo da važi za sve neparne brojeve do 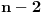 , i dokažimo za , i dokažimo za  . .Recimo da zadata kombinacija sadrži dva različito okrenuta novčića. Njih „markirajmo“, i u prva 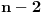 poteza možemo postići takvu situaciju da su svi novčići sem markiranih na željenim mestima: u svakom potezu obavezno okrenemo oba markirana novčića, što nam omogućuje da preostale naštimavamo po indukcijskoj hipotezi. Štaviše, markirani novčići ostaće međusobno na istoj strani (jer smo ih sve vreme prevrtali zajedno), u pretposlednjem potezu okrenućemo oba, i u poslednjem (u kom okrećemo samo jedan novčić) možemo okrenuti odgovarajući (podsetimo se, markirani novčići su u zadatoj kombinaciji različito okrenuti). poteza možemo postići takvu situaciju da su svi novčići sem markiranih na željenim mestima: u svakom potezu obavezno okrenemo oba markirana novčića, što nam omogućuje da preostale naštimavamo po indukcijskoj hipotezi. Štaviše, markirani novčići ostaće međusobno na istoj strani (jer smo ih sve vreme prevrtali zajedno), u pretposlednjem potezu okrenućemo oba, i u poslednjem (u kom okrećemo samo jedan novčić) možemo okrenuti odgovarajući (podsetimo se, markirani novčići su u zadatoj kombinaciji različito okrenuti).Ukoliko je zadata kombinacija takva da su svi novčići okrenuti na istu stranu, poređamo ih ukrug i, krenuvši od proizvoljnog, novčiće okrećemo redom kako stoje po krugu, u svakom potezu nastavljajući tamo gde smo stali u prethodnom. Dokazaćemo da će tako na kraju opet svi novčići biti jednako okrenuti. Zaista, ukupan broj okretanja je 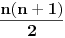 . Kako je . Kako je  neparan, broj okretanja deljiv je sa neparan, broj okretanja deljiv je sa  , pa kad ovako okrećemo „redom“, jasno je da ćemo se zaustaviti u pravom momentu (upravo nakon što svaki novčić okrenemo po , pa kad ovako okrećemo „redom“, jasno je da ćemo se zaustaviti u pravom momentu (upravo nakon što svaki novčić okrenemo po 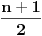 puta. puta.Time je dokaz indukcijom završen. Iz toga neposredno sledi tvrđenje prvog dela zadatka: izvršićemo unazad seriju poteza kojom se od postavke s novčićima dolazi do početne postavke (koju posmatramo kao zadatu). Ostaje još dokaz tvrđenja da je kraj jedinstveno određen. Pretpostavimo da se u jednom slučaju dobije jedna završna kombinacija, a u nekom drugom — druga. Primetimo da se tada broj okretanja svakog pojedinačnog novčića u prvom i drugom slučaju razlikuje za neparan broj, a budući da je i  neparno, ukupna razlika u broju okretanja takođe je neparan broj; međutim, kako je ukupan broj okretanja konstantan (gore je izračunato i koliko iznosi), ova razlika morala bi da bude neparno, ukupna razlika u broju okretanja takođe je neparan broj; međutim, kako je ukupan broj okretanja konstantan (gore je izračunato i koliko iznosi), ova razlika morala bi da bude  . Kontradikcija. . Kontradikcija.[ uranium @ 14.09.2007. 07:12 ] @
@Bojan Basic:
Zaista elegantno rešenje Zadatak se može shvatiti i ovako: Imamo proizvoljan binaran niz  dužine 2007 (dakle, jedini članovi niza su nule i jedinice). dužine 2007 (dakle, jedini članovi niza su nule i jedinice). Na njega dejstvujemo serijom  binarnih nizova (svaki od njih dužine 2007) uz pomoć operacije xor. binarnih nizova (svaki od njih dužine 2007) uz pomoć operacije xor.Za svako 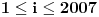 broj jedinica u nizu broj jedinica u nizu  je tačno je tačno  . .Operacija xor je komutativna, asocijativna a zbog 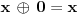 i i 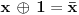 uz odgovarajuću "masku" može da se koristi kao invertor... uz odgovarajuću "masku" može da se koristi kao invertor...Rešenje je izuzetno jednostavno, ali je formalizacija tu činjenicu uspela da prikrije Pokazaćemo da se svaki polazni niz  može prevesti u konfiguraciju sa svim nulama/jedinicama (u zavisnosti od parnosti broja jedinica koje se pojavljuju u može prevesti u konfiguraciju sa svim nulama/jedinicama (u zavisnosti od parnosti broja jedinica koje se pojavljuju u  ). Neka je ). Neka je 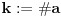 (broj jedinica u nizu (broj jedinica u nizu  ). ).Označimo sa 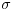 bilo koju permutaciju koja sve jedinice niza bilo koju permutaciju koja sve jedinice niza  premešta na početak niza - dakle, premešta na početak niza - dakle, 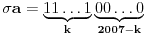 . . zbog preglednosti neću pisati zagrade kod upotrebe f-ja Konstruisaćemo nizove  čijim dejstvom invertujemo ili sve jedinice ili sve nule u čijim dejstvom invertujemo ili sve jedinice ili sve nule u 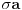 i na kraju ćemo odraditi i na kraju ćemo odraditi 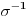 nad tim nizovima. nad tim nizovima.Odaberimo nizove  tako da za svako tako da za svako 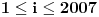 važi važi 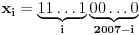 . .Neka je 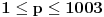 proizvoljno. Sada za svako proizvoljno. Sada za svako 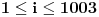 ( (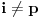 ) označimo sa ) označimo sa 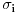 permutaciju za koju je permutaciju za koju je 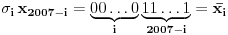 Sada vidimo da je 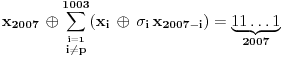 a da je a da je 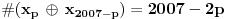 . .Neka je 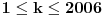 1. ako je  neparno, onda možemo pronaći neparno, onda možemo pronaći 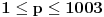 tako da je tako da je 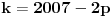 . Neka je . Neka je 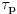 permutacija koja radi "neoznačeni permutacija koja radi "neoznačeni  mesta. Onda ostaje samo da odradimo mesta. Onda ostaje samo da odradimo 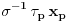 , , 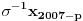 i i 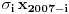 za za 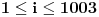 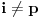 . Tako dobijenom serijom nizova možemo invertovati datih . Tako dobijenom serijom nizova možemo invertovati datih  jedinica u jedinica u  . .2. ako je  parno, onda je parno, onda je 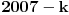 neparno pa menjamo cilj: želimo da invertujemo onih poslednjih neparno pa menjamo cilj: želimo da invertujemo onih poslednjih 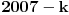 nula u nizu nula u nizu 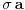 - dakle imamo da je - dakle imamo da je 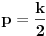 (setimo se - treba da važi (setimo se - treba da važi 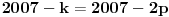 ) pa ostaje još samo da odradimo ) pa ostaje još samo da odradimo 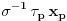 , , 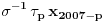 i i 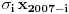 za za 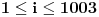 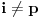 . .Ako je 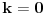 ili ili 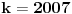 rešenje se dobija izvršavanjem rešenje se dobija izvršavanjem 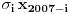 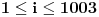 (dakle, ovog puta uključujući i (dakle, ovog puta uključujući i 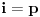 ). ).Iz konstrukcije je jasno da sledi i jedinstvenost (ako imamo neparan/paran broj jedinica u polaznom nizu - na kraju ćemo imati sve jedinice/nule). Metod koji je izložen može bez poteškoća biti uopšten za svako 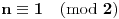 . .[Ovu poruku je menjao uranium dana 14.09.2007. u 10:00 GMT+1] [ cassey @ 14.09.2007. 19:13 ] @
[ Bojan Basic @ 15.09.2007. 01:23 ] @
@uranium:
Mrzim formalizaciju, ako me ikad iko pita zašto — pokazaću mu tvoju poruku. Uglavnom, bio sam siguran da tako nešto može proći (zato sam i napisao kako mi se čini da sam malo iskomplikovao), ali ona indukcija mi se prva nametnula. No, uprkos mojim osećanjima prema formalizmu, pažljivo sam, kao svaki dobar referi, proučio tvoje rešenje, i mislim da sam uhvatio nekoliko grešaka (svakako ne suštinskih): Citat: Druga transformacija treba da bude 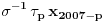 , ali ovo je očito samo greška u kucanju. No, čini mi se da je definicija transformacije , ali ovo je očito samo greška u kucanju. No, čini mi se da je definicija transformacije 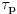 pogrešna; naime, da bi ovo prošlo, moramo pogrešna; naime, da bi ovo prošlo, moramo 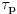 definisati kao kružni pomeraj ulevo (dakle, ne udesno). Jesam li u pravu? definisati kao kružni pomeraj ulevo (dakle, ne udesno). Jesam li u pravu?Uz malopređašnju ispravku oko definicije 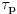 , na samom startu trebalo je , na samom startu trebalo je 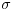 definisati tako da na početku niza nagomila onu cifru koja se pojavljuje neparan broj puta (a ne obavezno jedinicu). definisati tako da na početku niza nagomila onu cifru koja se pojavljuje neparan broj puta (a ne obavezno jedinicu).Citat: Iz konstrukcije je jasno da sledi i jedinstvenost (ako imamo neparan/paran broj jedinica u polaznom nizu - na kraju ćemo imati sve jedinice/nule). Hm, ovde me nisi ubedio. @cassey: Citat: Ako misliš na situaciju kada su na početku, kao i na kraju, svi novčići okrenuti na istu stranu (čini mi se da u opštem slučaju okretanje proizvoljnim redom ništa ne pomaže, čak i malo komplikuje), da, slažem se da ovo malo pojednostavljuje stvari u odnosu na ono moje obrtanje po krugu. Uzgred, nemoj još objavljivati rešenje prvog i pojačanog trećeg, baš mi dobro dođe da se malo razgibavam ovih dana. [ uranium @ 15.09.2007. 16:19 ] @
Citat: Guilty as charged  "... i da ne nabrajam još sjaset sličnih situacija nakon kojih sam bio prinuđen [ne bih li izbegao postispitne traume "... i da ne nabrajam još sjaset sličnih situacija nakon kojih sam bio prinuđen [ne bih li izbegao postispitne traume Citat: Bojan Basic: Međutim, među programerima postoji jedna zanimljiva izreka: stil programiranja je kao ... (da ne psujem sad) — svako ima svoj, i niko ne voli tuđ. Mislim da bi se nešto slično moglo primeniti i na rešavanje matematičkog problema Potpuno se slažem, čak sam se u dva maha vraćao da to prepravim... i svaki put odustajao Izgleda da bi trebalo opet da pročitam How to write mathematics - vrlo simpatičan esej Pola Halmoša... Citat: Bojan Basic: No, uprkos mojim osećanjima prema formalizmu, pažljivo sam, kao svaki dobar referi, proučio tvoje rešenje, i mislim da sam uhvatio nekoliko grešaka (svakako ne suštinskih): Citat: uranium Neka je 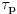 permutacija koja radi "neoznačeni permutacija koja radi "neoznačeni  mesta. Onda ostaje samo da odradimo mesta. Onda ostaje samo da odradimo 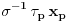 , , 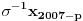 Druga transformacija treba da bude 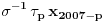 , ali ovo je očito samo greška u kucanju. No, čini mi se da je definicija transformacije pogrešna; naime, da bi ovo prošlo, moramo definisati kao kružni pomeraj ulevo (dakle, ne udesno). Jesam li u pravu? , ali ovo je očito samo greška u kucanju. No, čini mi se da je definicija transformacije pogrešna; naime, da bi ovo prošlo, moramo definisati kao kružni pomeraj ulevo (dakle, ne udesno). Jesam li u pravu?U pravu si da u tom delu postoji greška ali ne baš to... Cilj mi je bio da se 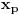 i i 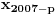 rasporede tako da njihovo xor-ovanje daje niz u kome se svih rasporede tako da njihovo xor-ovanje daje niz u kome se svih 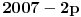 jedinica nalazi na početku. Dakle, ne želim da pomeram jedinica nalazi na početku. Dakle, ne želim da pomeram 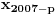 već samo već samo 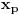 i to ne za i to ne za  mesta kako sam pogrešno napisao, već za mesta kako sam pogrešno napisao, već za 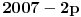 ...znači ispravka: umesto ...znači ispravka: umesto 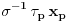 treba da stoji treba da stoji 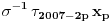 Citat: Bojan Basic: ...na samom startu trebalo je 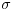 definisati tako da na početku niza nagomila onu cifru koja se pojavljuje neparan broj puta (a ne obavezno jedinicu). definisati tako da na početku niza nagomila onu cifru koja se pojavljuje neparan broj puta (a ne obavezno jedinicu).Da, to bi skratilo dokaz... mada mi je ionako prva namera bila da samo kažem "drugi slučaj se svodi na prvi..." Citat: Bojan Basic: Citat: uranium Iz konstrukcije je jasno da sledi i jedinstvenost (ako imamo neparan/paran broj jedinica u polaznom nizu - na kraju ćemo imati sve jedinice/nule). Hm, ovde me nisi ubedio. Slažem se da tvoja procedura izbacuje sve jedinice ili nule u zavisnosti od parnosti broja početnih jedinica, ali trebalo bi dokazati da to važi za svaku proceduru; čini mi se da to nije očigledno iz tvog rešenja, već da bi se jedinstvenost morala zasebno dokazati. Stvar je opet užasno prosta... samo ja očito retko kad ukapiram šta treba objašnjavati a šta ne Ako bi bilo koja procedura dobijala suprotno od one moje, ona bi morala biti u stanju da invertuje paran broj jedinica ili nula, a to nije moguće, jer u onih ključnih 2006 nizova (poslednji 2007. ne uzimam u obzir jer on invertuje sve) ima neparan broj jedinica ( 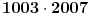 ), od toga paran broj jedinica moram da potrošim da bih određene elemente ostavio u konačnom neinvertovane, dakle, ostaje mi neparan broj jedinica da potrošim... a da bih invertovao paran broj ma čega, potreban mi je paran broj "grupa" sa po neparno mnogo jedinica. Dakle, nema takve procedure ), od toga paran broj jedinica moram da potrošim da bih određene elemente ostavio u konačnom neinvertovane, dakle, ostaje mi neparan broj jedinica da potrošim... a da bih invertovao paran broj ma čega, potreban mi je paran broj "grupa" sa po neparno mnogo jedinica. Dakle, nema takve procedure Na kraju, hvala Bojanu na konstruktivnoj kritici i otkrivenoj grešci, a svima koji su pročitali moj prethodni post se izvinjavam jer skoro da nema dela koji nije zreo za refactoring [ Bojan Basic @ 15.09.2007. 22:42 ] @
Citat: uranium: U pravu si da u tom delu postoji greška ali ne baš to... Cilj mi je bio da se 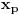 i i 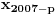 rasporede tako da njihovo xor-ovanje daje niz u kome se svih rasporede tako da njihovo xor-ovanje daje niz u kome se svih 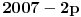 jedinica nalazi na početku. Dakle, ne želim da pomeram jedinica nalazi na početku. Dakle, ne želim da pomeram 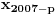 već samo već samo 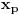 i to ne za i to ne za  mesta kako sam pogrešno napisao, već za mesta kako sam pogrešno napisao, već za 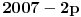 ...znači ispravka: umesto ...znači ispravka: umesto 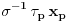 treba da stoji treba da stoji 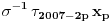 Jasno mi je šta je cilj, s tim što sam ga ja postigao pomerajući oba člana (ali drugom transformacijom). Po mome — dakle, kružnim pomerajem ulevo — bilo bi: 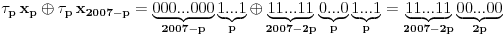 No, jasno je da može i kao što si se ispravio. Princip je isti, sve su ostalo nijanse. [ cassey @ 19.09.2007. 02:23 ] @
Evo malo primenjene matematike :)
(mislim da je autor imao previse slobodnog vremena) http://alas.matf.bg.ac.yu/~djole/kakopedija/ [ Bojan Basic @ 23.09.2007. 20:18 ] @
Evo rešenja prvog. Zasnovano je na Farenhajtovoj ideji s centralnom simetrijom.
Povucimo kroz tačku  proizvoljnu pravu, i neka je proizvoljnu pravu, i neka je  tačka najbliža tački tačka najbliža tački  u preseku date krive u preseku date krive 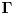 i povučene prave, a i povučene prave, a  najdalja (ukoliko se dogodi da imamo dve na jednakom rastojanju — tj. dve najbliže ili dve najdalje — one jasno moraju biti s različitih strana tačke najdalja (ukoliko se dogodi da imamo dve na jednakom rastojanju — tj. dve najbliže ili dve najdalje — one jasno moraju biti s različitih strana tačke  , pa je zadatak rešen). Smemo govoriti o najbližoj tački zahvaljujući neprekidnosti krive , pa je zadatak rešen). Smemo govoriti o najbližoj tački zahvaljujući neprekidnosti krive 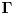 : zaista, odaberimo infimum, s obzirom na udaljenost od : zaista, odaberimo infimum, s obzirom na udaljenost od  , skupa presečnih tačaka posmatrane prave i , skupa presečnih tačaka posmatrane prave i 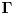 , pa i on mora pripadati krivoj , pa i on mora pripadati krivoj 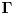 ; slično rezonujemo za najdalju tačku. ; slično rezonujemo za najdalju tačku.Neka je 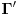 , , 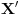 i i 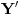 centralnosimetrična slika objekata centralnosimetrična slika objekata 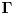 , ,  i i  , redom, u odnosu na tačku , redom, u odnosu na tačku  (odmah primetimo (odmah primetimo 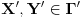 . Želimo pokazati da se . Želimo pokazati da se 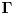 i i 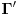 moraju seći, iz čega neposredno sledi zaključak zadatka. U to ime, primetimo da moraju seći, iz čega neposredno sledi zaključak zadatka. U to ime, primetimo da 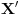 pripada unutrašnjosti krive pripada unutrašnjosti krive 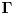 (zapravo, cela duž (zapravo, cela duž 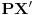 pripada unutrašnjosti krive pripada unutrašnjosti krive 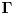 , jer bi u suprotnom duž , jer bi u suprotnom duž 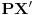 presekla krivu u tački koja je tački presekla krivu u tački koja je tački  bliža nego tačka bliža nego tačka  , što je u suprotnosti s izborom tačke , što je u suprotnosti s izborom tačke  ), dok ), dok 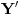 pripada njenoj spoljašnjosti (rezon je sličan). Dakle, svaka neprekidna kriva koja ih povezuje, pa tako i kriva pripada njenoj spoljašnjosti (rezon je sličan). Dakle, svaka neprekidna kriva koja ih povezuje, pa tako i kriva 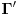 (zapravo, jedan njen luk), mora preseći krivu (zapravo, jedan njen luk), mora preseći krivu 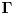 . .[Ovu poruku je menjao Bojan Basic dana 21.03.2009. u 16:43 GMT+1] [ cassey @ 23.09.2007. 20:54 ] @
Upravo tako :)
[ uranium @ 23.09.2007. 21:23 ] @
Možda je zanimljivo spomenuti da je 1977. upravo to bio zadatak B4 na čuvenom The William Lowell Putnam Mathematical Competition
Ovde možete videti još jedan zanimljiv pristup (koji je dovoljno dobar u slučaju konveksnih krivih) a takođe i varijantu Farenhajt - Bašićeve ideje... [ Bojan Basic @ 24.09.2007. 03:01 ] @
Slažem se da je gornji pristup na uraniumovom linku dovoljno dobar za konveksne krive, ali, kad je to već pomenuto, naglasio bih kako autor greši u pretpostavci da bi se greška mogla prevazići. Naime, pretpostavljam da je mislio kako bismo mogli ići „malo napred pa nazad“ tako da obe tačke zaista simultano obiđu krivu, ali mu argument pada kod nekih malo neintuitivnijih krivih, poput onih koje sadrže deo funkcije
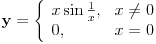 . Jednostavno, kada dođemo u blizinu nule, samo ćemo „talasati“ do beskonačnosti, tuda nikad nećemo proći (iako kriva jeste neprekidna!). Ovo nije prvi put da neko upadne u tu zamku: Čarls Stenli Ogilvi (C. S. Ogilvy) polovinom prošlog veka verovao je da je rešio problem (i dalje otvoren) o upisivanju kvadrata u krivu (više informacija o tome ovde, a fina lista referenaca i informacije o najsvežijem progresu mogu se videti ovde). Njegov dokaz kasnije je osporen s više strana, a meni se čini da bi se sve moglo okrpiti osim upravo krivih poput navedene. (Mada, i pored svega, mislim da je njegov pokušaj prošao previše nezapaženo. Ne sećam se više kako sam ga ja pronašao pošto je bilo davno, ali sad nisam uspeo da nađem nijednu referencu na njegov rad.) Dokaz i kritika nalaze se u prilogu. . Jednostavno, kada dođemo u blizinu nule, samo ćemo „talasati“ do beskonačnosti, tuda nikad nećemo proći (iako kriva jeste neprekidna!). Ovo nije prvi put da neko upadne u tu zamku: Čarls Stenli Ogilvi (C. S. Ogilvy) polovinom prošlog veka verovao je da je rešio problem (i dalje otvoren) o upisivanju kvadrata u krivu (više informacija o tome ovde, a fina lista referenaca i informacije o najsvežijem progresu mogu se videti ovde). Njegov dokaz kasnije je osporen s više strana, a meni se čini da bi se sve moglo okrpiti osim upravo krivih poput navedene. (Mada, i pored svega, mislim da je njegov pokušaj prošao previše nezapaženo. Ne sećam se više kako sam ga ja pronašao pošto je bilo davno, ali sad nisam uspeo da nađem nijednu referencu na njegov rad.) Dokaz i kritika nalaze se u prilogu.Elem, kad se uranium već potrudio da locira zadatak, ne bi mi mrsko da potražim zvanično rešenje. Nešto je (očekivano?) jednostavnije od viđenih. U slobodnoj interpretaciji: Krive 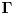 i i 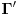 moraju se seći jer obe sadrže moraju se seći jer obe sadrže  (dakle, ne može biti jedna u spoljašnjosti druge) i imaju isti prečnik. (dakle, ne može biti jedna u spoljašnjosti druge) i imaju isti prečnik. [ uranium @ 24.09.2007. 18:55 ] @
Lep primer sa
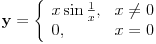 ... ali izgleda da te je Zenon upecao [ "niti možemo stići u nulu, niti možemo iz nje poći" ... ali izgleda da te je Zenon upecao [ "niti možemo stići u nulu, niti možemo iz nje poći" Dakle, čudi me tvoj zaključak o neprolasku kad si lepo primetio da je f-ja neprekidna... znači, možeš da izračunaš "kad" ćeš biti u bilo kojoj tački uključujući i (0,0) i veruj mi da će to "kad" biti različito od "nikad" Tako da do daljnjeg Što se tiče upisivanja kvadrata, trenutno nemam vremena da detaljnije pogledam sav materijal, ali jasno je da je problem izuzetno uzbudljiv - tako da u ime nas koji za njega nismo čuli do sad - veliko hvala! Fajlovi koje si ostavio su identični...(upload glitch?!)... u prilogu ove poruke je (nadam se) onaj nameravani sa kritikama. [ Bojan Basic @ 24.09.2007. 19:19 ] @
Citat: uranium: Dakle, čudi me tvoj zaključak o neprolasku kad si lepo primetio da je f-ja neprekidna... znači, možeš da izračunaš "kad" ćeš biti u bilo kojoj tački uključujući i (0,0) i veruj mi da će to "kad" biti različito od "nikad" I dalje mi se čini mi da i pored toga (što svakako stoji, nisam ni pokušavao da osporim) nećemo proći, jer prolazak ne vezujemo za vreme već za situaciju u kojoj smo. Dakle, situacija je otprilike: „Ako si došao na rub, u nastavku puta malo se vraćaš, pa zatim ideš napred do sledećeg ruba gde ćeš se opet malo vratiti...“ Dakle, ako ovako vežeš kretanje za te „povratke“, onda zaista nikad nećeš proći; vezivanje za vreme bi svakako bilo bolje (u ovom pogledu), ali samo ako je to uopšte moguće. Oba priložena fajla zaista su greškom bila identična (sad sam obrisao jedan). Svejedno, drugi nameravani je ovo što si ti pronašao. [ uranium @ 24.09.2007. 21:16 ] @
Da pokušam uz pomoć slike
[att_img] Recimo da se šetamo po onoj neverending sinusoidi [ Bojan Basic @ 24.09.2007. 22:37 ] @
Već smo se složili da to preslikavanje „preko neke tačke nazad na krivu“ ne prolazi čim dođemo do nekonveksnih krivih. Ovo što si ti prikazao upravo je ono vezivanje za vreme koje sam pominjao u prošloj poruci (u zavisnosti od toga gde se u određenom trenutku nalazi prva tačka, odaberemo drugu), ali pošto to, upravo rekosmo, ne valja, moramo naći drugi pristup.
Taj pristup sastoji se u tome da obe tačke mrdamo istovremeno, pazeći kad koju treba malo da vratimo. Pošto si se potrudio da mi nacrtaš  , i sad vidi šta se dešava: u jednom momentu tačka , i sad vidi šta se dešava: u jednom momentu tačka  (recimo da smo krenuli s njom nadesno) doći će na ovo „ispupčenje“ (tada će posmatrana prava lokalno biti tangenta na datu krivu u tački (recimo da smo krenuli s njom nadesno) doći će na ovo „ispupčenje“ (tada će posmatrana prava lokalno biti tangenta na datu krivu u tački  ), i ne bi mogao da nastaviš okretanje kako si počeo; da bi nastavio obilazak, moraš sad okretati tako da se tačka ), i ne bi mogao da nastaviš okretanje kako si počeo; da bi nastavio obilazak, moraš sad okretati tako da se tačka  vraća; to će trajati dok tačka vraća; to će trajati dok tačka  ne dođe u „udubljenje“, pa onda tačka ne dođe u „udubljenje“, pa onda tačka  opet kreće napred. Moguće je da sam ovo konfuzno objasnio, ali verujem da ćeš shvatiti, jer je u suštini stvarno jednostavno. Samo još primeti da smo u istu situaciju mogli doći i s tačkom opet kreće napred. Moguće je da sam ovo konfuzno objasnio, ali verujem da ćeš shvatiti, jer je u suštini stvarno jednostavno. Samo još primeti da smo u istu situaciju mogli doći i s tačkom  , pa bismo onda tačku , pa bismo onda tačku  „vraćali“, i tako kad koja dođe na red. „vraćali“, i tako kad koja dođe na red.Time smo dobili neki postupak za obilazak cele krive, tako što „ispupčenja“ i „udubljenja“ obradimo jedno po jedno. Međutim, tu leži problem sa spornom krivom: kada jedna od tačaka dođe do okoline nule, šablon nam nalaže da postupamo tako što idemo na jednu stranu dokle treba, pa na drugu dokle treba, pa na prvu dokle treba, pa na drugu dokle treba... i tako mi prolazimo bregove i doline jedno po jedno, a ovo „dokle treba“ stalno će iskakati (i svaki put će „trebati“ manje, ali to nam ne umanjuje tugu). [ uranium @ 25.09.2007. 01:04 ] @
Ovo već postaje komično
Citat: Bojan Basic: Taj pristup sastoji se u tome da obe tačke mrdamo istovremeno, pazeći kad koju treba malo da vratimo. Pošto si se potrudio da mi nacrtaš  , i sad vidi šta se dešava: u jednom momentu tačka , i sad vidi šta se dešava: u jednom momentu tačka  (recimo da smo krenuli s njom nadesno) doći će na ovo „ispupčenje“ (tada će posmatrana prava lokalno biti tangenta na datu krivu u tački (recimo da smo krenuli s njom nadesno) doći će na ovo „ispupčenje“ (tada će posmatrana prava lokalno biti tangenta na datu krivu u tački  ), i ne bi mogao da nastaviš okretanje kako si počeo; da bi nastavio obilazak, moraš sad okretati tako da se tačka ), i ne bi mogao da nastaviš okretanje kako si počeo; da bi nastavio obilazak, moraš sad okretati tako da se tačka  vraća; to će trajati dok tačka vraća; to će trajati dok tačka  ne dođe u „udubljenje“, pa onda tačka ne dođe u „udubljenje“, pa onda tačka  opet kreće napred. Moguće je da sam ovo konfuzno objasnio, ali verujem da ćeš shvatiti, jer je u suštini stvarno jednostavno. Samo još primeti da smo u istu situaciju mogli doći i s tačkom opet kreće napred. Moguće je da sam ovo konfuzno objasnio, ali verujem da ćeš shvatiti, jer je u suštini stvarno jednostavno. Samo još primeti da smo u istu situaciju mogli doći i s tačkom  , pa bismo onda tačku , pa bismo onda tačku  „vraćali“, i tako kad koja dođe na red. „vraćali“, i tako kad koja dođe na red.Opis je sasvim jasan, i upravo to sam i hteo da kažem onim crtežom... samo obrneš stvari - šta je bio kodomen sada uzmeš da je domen... Naravno, čak i ako se ograničimo samo na ovaj thread, to ne bi bio prvi put da jedan drugome objašnjavamo ono što drugi već zna Doduše...verovatno sam ja to radio češće... Citat: Bojan Basic: Time smo dobili neki postupak za obilazak cele krive, tako što „ispupčenja“ i „udubljenja“ obradimo jedno po jedno. Međutim, tu leži problem sa spornom krivom: kada jedna od tačaka dođe do okoline nule, šablon nam nalaže da postupamo tako što idemo na jednu stranu dokle treba, pa na drugu dokle treba, pa na prvu dokle treba, pa na drugu dokle treba... i tako mi prolazimo bregove i doline jedno po jedno, a ovo „dokle treba“ stalno će iskakati (i svaki put će „trebati“ manje, ali to nam ne umanjuje tugu). Ja se zaista izvinjavam što postajem periodičan Ako se i dalje ne budemo slagali [ a verovatno nećemo biti te sreće Hajde da vidimo ovakav primer: neka je 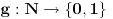 i neka je i neka je 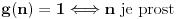 jasno je da imamo algoritam koji nam posle konačno mnogo koraka nedvosmisleno govori da li je dati broj prost ili nije. Da li bi ti sad prihvatio da je f-ja  dobro definisana na celom dobro definisana na celom 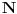 ? ?Ako ne prihvataš - onda je to tvoj filozofski stav i ja to apsolutno poštujem, pa je to onda kraj nesporazumima [ Bojan Basic @ 26.09.2007. 01:40 ] @
Citat: Prihvatio bih, naravno (nikad ne uplićem filozofske stavove u rešavanje matematičkih problema). Citat: uranium: a ako prihvataš, e onda bih voleo da mi objasniš u čemu je suštinska razlika između te i one prethodne situacije sa krivom Manja razlika je u tome što tvoja funkcija za jedan broj izbaci jednu vrednost bez ikakvih problema, dok u našem slučaju moramo pratiti šta se dešavalo od samog početka. Veća razlika je u tome što jesam prihvatio da je funkcija definisana na celo 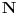 , ali nije definisana u tački , ali nije definisana u tački  . Kao što možeš da zaređaš po prirodnim brojevima i do svakog konkretnog bi stigao pre ili kasnije, tako možeš da zaređaš i po onim bregovima i svaki konkretan bi došao na red pre ili kasnije, ali ne i koordinatni početak (koji je „iza“ svih njih, kao što je . Kao što možeš da zaređaš po prirodnim brojevima i do svakog konkretnog bi stigao pre ili kasnije, tako možeš da zaređaš i po onim bregovima i svaki konkretan bi došao na red pre ili kasnije, ali ne i koordinatni početak (koji je „iza“ svih njih, kao što je  „iza“ svih prirodnih brojeva). „iza“ svih prirodnih brojeva).Da rekapituliramo stvari. Prvo smo imali konveksne krive i postupak za njih (vrtimo jednu tačku, drugu uzimamo u jedinstveno preseku). Onda smo unapredili postupak tako da prelazi i ispupčenja; jasno je, ako pređe jedno, onda može i konačno mnogo. E sad bi trebalo još da unapredimo da prolazi beskonačno mnogo ispupčenja. Ti tvrdiš da možemo uzeti limes i da će sve biti OK, a meni to jednostavno nije dovoljno čisto: najpre uopšteno, a zatim i na osnovu čega tvrdiš da ćemo time zaobići i sve patološke slučaje (recimo, ni na osnovu čega ne možemo tvrditi da po 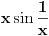 idemo pravo prema nuli; ako se nešto „dešava“ s druge strane, onda ćemo morati i po ovim talasićima da idemo napred-nazad, a ne samo da ih pratimo do nule). Štaviše, možemo primetiti da se prelaz između prve situacije (konveksne krive) i druge zasnovao na obradi „specijalnih“ tačaka (onih na vrhu „brega“ i na dnu „doline“), te smo rekli šta treba raditi kad dođemo do njih. Moraćeš se složiti da u trećem scenariju imamo jednu još „specijalniju“ tačku (nulu), jer se ona ne uklapa u tačke s kojima smo do sada radili, pa očekujem da će krpljenje tog slučaja uključivati i neko uputstvo u vezi s tom tačkom. Reći da limes pušten kroz drugi slučaj pokriva sve odjednom suviše mi je klimavo. idemo pravo prema nuli; ako se nešto „dešava“ s druge strane, onda ćemo morati i po ovim talasićima da idemo napred-nazad, a ne samo da ih pratimo do nule). Štaviše, možemo primetiti da se prelaz između prve situacije (konveksne krive) i druge zasnovao na obradi „specijalnih“ tačaka (onih na vrhu „brega“ i na dnu „doline“), te smo rekli šta treba raditi kad dođemo do njih. Moraćeš se složiti da u trećem scenariju imamo jednu još „specijalniju“ tačku (nulu), jer se ona ne uklapa u tačke s kojima smo do sada radili, pa očekujem da će krpljenje tog slučaja uključivati i neko uputstvo u vezi s tom tačkom. Reći da limes pušten kroz drugi slučaj pokriva sve odjednom suviše mi je klimavo.I za kraj, vrlo sličan argument upotrebljen je u tekstu koji sam okačio (mi ovde rotiramo pravu oko tačke  , tamo je transliramo gore-dole), a ovo mu je pronađeno kao jedan od propusta. Procenio sam (mada, naravno, uvek postoji šansa da grešim) da je ovo i najteže prevazići; dakle, ako uspeš da ubediš matematičku zajednicu kako se taj slučaj pokriva jednostavnom nadgradnjom prethodnog, eto ti šanse da rešiš problem star stotinak godina. , tamo je transliramo gore-dole), a ovo mu je pronađeno kao jedan od propusta. Procenio sam (mada, naravno, uvek postoji šansa da grešim) da je ovo i najteže prevazići; dakle, ako uspeš da ubediš matematičku zajednicu kako se taj slučaj pokriva jednostavnom nadgradnjom prethodnog, eto ti šanse da rešiš problem star stotinak godina. [ Nedeljko @ 26.09.2007. 13:51 ] @
Ako raspravljate o prvom zadatku, probao bih ja da ga rešim:
Neka je 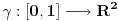 proizvoljna zatvorena, neprekidna, nesamopresecajuća kriva. Po Kantorovoj teoremi o ravnomernoj neprekidnosti postoji niz proizvoljna zatvorena, neprekidna, nesamopresecajuća kriva. Po Kantorovoj teoremi o ravnomernoj neprekidnosti postoji niz 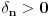 koji teži nuli i takav da za ma koje koji teži nuli i takav da za ma koje 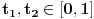 važi važi 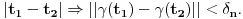 Za ma koje Za ma koje  definišimo krivu definišimo krivu 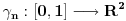 na sledeći način: na sledeći način: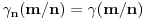 za ma koje za ma koje 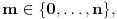 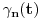 je linearno po je linearno po  na intervalu na intervalu 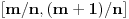 za ma koje za ma koje  Neka je  Tada za ma koje Tada za ma koje 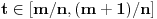 važi važi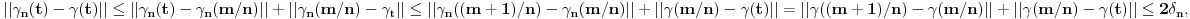 što znači da niz 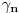 ravnomerno konvergira ka ravnomerno konvergira ka 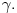 Naglašavam da je nejednakost Naglašavam da je nejednakost 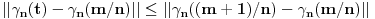 posledica linearnosti funkcije posledica linearnosti funkcije 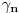 na intervalu na intervalu 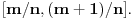 Pošto sve ove funkcije uzimaju iste vrednosti u tačkama 0 i 1, možemo ih produžiti do 1-periodičnih funkcija na  . Tada za svako . Tada za svako  postoji rastuća, neprekidna, 1-periodična funkcija postoji rastuća, neprekidna, 1-periodična funkcija 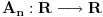 takva da su tačke takva da su tačke 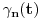 i i 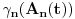 krajevi duži na kojoj leži data tačka krajevi duži na kojoj leži data tačka  i tako da važi jednakost i tako da važi jednakost 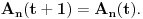 Ovo me mrzi da dokazujem, ali se nadam da barem poligoni nisu problematični, čak i u slučaju kada se samopresecaju, mada sve treba proveriti. Ovo me mrzi da dokazujem, ali se nadam da barem poligoni nisu problematični, čak i u slučaju kada se samopresecaju, mada sve treba proveriti.Za svako  postojaće neko postojaće neko 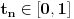 takvo da je tačka takvo da je tačka  središte duži sa krajevima središte duži sa krajevima 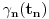 i i 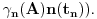 Pošto se sve te tačke nalaze u ograničenom podskupu od Pošto se sve te tačke nalaze u ograničenom podskupu od 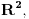 postoji rastući niz priridnih brojeva postoji rastući niz priridnih brojeva 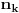 takav da niz takav da niz 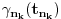 konvergira ka nekoj tački konvergira ka nekoj tački 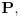 niz niz 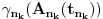 konvergira ka nekoj tački konvergira ka nekoj tački  i niz i niz 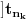 konvergira ka nekom konvergira ka nekom 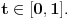 Jasno je da na osnovu neprekidnosti metrike tada tačka Jasno je da na osnovu neprekidnosti metrike tada tačka  mora biti središte duži sa krajevima mora biti središte duži sa krajevima  i i 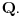 Na osnovu ravnomerne konvergencije niza 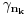 ka ka 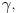 važi važi 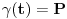 i i 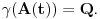 [ uranium @ 27.09.2007. 05:18 ] @
@Nedeljko:
Iz dokaza deluje kao da je trebalo da stoji 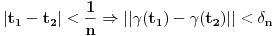 . .Citat: Nedeljko: Pošto sve ove funkcije uzimaju iste vrednosti u tačkama 0 i 1, možemo ih produžiti do 1-periodičnih funkcija na  . Tada za svako . Tada za svako  postoji rastuća, neprekidna, 1-periodična funkcija postoji rastuća, neprekidna, 1-periodična funkcija 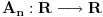 takva da su tačke takva da su tačke 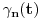 i i 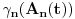 krajevi duži na kojoj leži data tačka krajevi duži na kojoj leži data tačka  i tako da važi jednakost i tako da važi jednakost 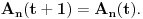 Ovo me mrzi da dokazujem, ali se nadam da barem poligoni nisu problematični, čak i u slučaju kada se samopresecaju, mada sve treba proveriti. Ovo me mrzi da dokazujem, ali se nadam da barem poligoni nisu problematični, čak i u slučaju kada se samopresecaju, mada sve treba proveriti.Kod konkavnih krivih (pa i konk. poligona) neizostavno mora doći do kretanja "napred-nazad" [prosto ne mogu da verujem da to opet pominjemo @Bojan Basic: Meni je sasvim dovoljno da si se složio za konačne ordinale. Čini mi se da se relativno lako može napraviti sličan primer koji bi zadovoljio i onaj prvi kriterijum koji si naveo [zavisnost tekućeg od prethodnih] [evo recimo, pada mi na pamet Kantorova dijagonalizacija, protiv koje nemaš ništa, ako se dobro sećam Dalje, čini mi se da ti sad pokušavaš da malo zameniš uloge Evo sad sam naškrabao slučaj, kada je kriva ograničena sa: 1. 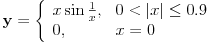 2. 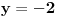 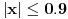 3. 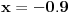 4. 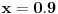 izaberem recimo 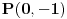 i lepo krenem da povlačim linije kroz nju krećući se po onoj sinusoidnoj krivoj od tačke recimo i lepo krenem da povlačim linije kroz nju krećući se po onoj sinusoidnoj krivoj od tačke recimo 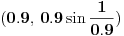 ka tački ka tački 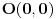 . .Posle kraćeg računa dobija se da su odgovarajući preseci na "donjoj" strani dati sa 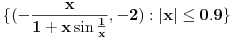 ... Dakle, nikakvih poteškoća nije bilo u 0. [u toku izvođenja formule treba isključiti nulu iz razmatranja, ali se nakon toga ispostavi (gle čuda) da se limes poslednje formule kad ... Dakle, nikakvih poteškoća nije bilo u 0. [u toku izvođenja formule treba isključiti nulu iz razmatranja, ali se nakon toga ispostavi (gle čuda) da se limes poslednje formule kad 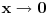 poklapa sa onim što direktno dobijamo spajajući poklapa sa onim što direktno dobijamo spajajući  i i  ] ]Da ponovim, [ kao da to ima neku svrhu Na kraju, u vezi sa rešavanjem problema upisivanja kvadrata... mislim da si ti trenutno bliži obaranju principa trasfinitne indukcije za ordinale a to bi, složićeš se, bio nemerljivo veći uspeh... [ petarm @ 29.09.2007. 16:38 ] @
I koji je problem na kraju resen?
[ Bojan Basic @ 30.09.2007. 13:45 ] @
Citat: uranium: Još jednom da naglasim, ja uopšte ne tvrdim da se ceo onaj postupak može spasiti, već samo tvrdim da ono što si izneo kao ključnu prepreku, izolovano gledano, nije prepreka. Uzmi običan kvadrat i malo mu „ulubi“ jednu stranicu. Neka je tačka  u njegovom centru. Očito, postupak koji smo imali za konveksne krive (dakle, onaj bez ikakvog vraćanja) savršeno funkcioniše i za ovaj kvadrat, iako je nekonveksan. Time sam ja „dokazao“ (nalazeći jedan kontraprimer) da nekonveksnost nije esencijalna prepreka za najprvi postupak. u njegovom centru. Očito, postupak koji smo imali za konveksne krive (dakle, onaj bez ikakvog vraćanja) savršeno funkcioniše i za ovaj kvadrat, iako je nekonveksan. Time sam ja „dokazao“ (nalazeći jedan kontraprimer) da nekonveksnost nije esencijalna prepreka za najprvi postupak. Ozbiljno, po mom poimanju nekonveksnost jeste prepreka za najprvi algoritam baš koliko je i singularitet prepreka za prvo poboljšanje (bez obzira na to što se u oba slučaja mogu naći kontraprimeri); ako ti se ne sviđaju imena „esencijalna prepreka“, „ključna prepreka“ itd., nazovi razlog prvog prelaza drugačije (recimo, „moguća prepreka“), pa to isto reci i za drugi prelaz. Iz tvoje rečenice koju sam gore citirao, čini mi se da smo se, s ovim razjašnjenjem, najzad složili. Rekao bih da je ovo kraj priče. A i kako je moglo drugačije da se završi sem beskonačnim ponavljanjem ukrug istih stvari dok ne ustanovimo kako se jednostavno međusobno ne razumemo. Nije nam prvi put. Citat: Rešeno je još odavno sve sem poboljšanog trećeg. Ova gomila poruka koju vidiš predstavlja samo razmatranje jednog drugačijeg pristupa prvom zadatku. [ Nedeljko @ 01.10.2007. 09:12 ] @
Pa, taj i nema rešenje. Sve što možeš da uradiš je da odvojiš na gomilu m novčića (ovde je iznuđeno 50), a onda nasumice okreneš n od tih 50 i k od onih preostalih 50. Sve ostalo što možeš da uradiš se svodi na to, jer na kraju postupka koji si primenio imaš na dve gomile po 50 novčića i na svakoj od njih po neki broj okrenutih i neki broj neokrenutih. Budući da su ti vezane oči, sve što si mogao da kontrolišeš je to koliko je prevrnutih na jednoj gomili, a koliko na drugoj. Lako se pokazuje da tako nema rešenje, a samim tim i nikako drugačije.
[ Bojan Basic @ 01.10.2007. 17:39 ] @
I dokaz da je nemoguće učiniti to što se traži jeste validno rešenje zadatka (doduše, postavljač nisam ja, ali verujem da će se cassey složiti). Međutim, ova tvoja skica dokaza ima poveću rupu. Naime, tvrdnju da je jedino potrebno razmatrati situaciju u kojoj okrećemo fiksnih
 s jedne gomile i s jedne gomile i  s druge obara strategija po kojoj prvo nešto okrenemo, a onda razdelimo. s druge obara strategija po kojoj prvo nešto okrenemo, a onda razdelimo.[ cassey @ 02.10.2007. 17:15 ] @
Citat: Nedeljko: Pa, taj i nema rešenje. Sve što možeš da uradiš je da odvojiš na gomilu m novčića (ovde je iznuđeno 50), a onda nasumice okreneš n od tih 50 i k od onih preostalih 50. Sve ostalo što možeš da uradiš se svodi na to, jer na kraju postupka koji si primenio imaš na dve gomile po 50 novčića i na svakoj od njih po neki broj okrenutih i neki broj neokrenutih. Budući da su ti vezane oči, sve što si mogao da kontrolišeš je to koliko je prevrnutih na jednoj gomili, a koliko na drugoj. Lako se pokazuje da tako nema rešenje, a samim tim i nikako drugačije. Hmmm... mislim da se slazem sa Bojanom (mada nisam bas siguran da sam ukapirao sta je receno). Trenutno ne mogu da se setim resenja, ali pogledacu nocas (u svakom slucaju na zadatak sam naisao negde na netu pa cu da potrazim isti) [ Nedeljko @ 03.10.2007. 12:35 ] @
Citat: Bojan Basic: Naime, tvrdnju da je jedino potrebno razmatrati situaciju u kojoj okrećemo fiksnih  s jedne gomile i s jedne gomile i  s druge obara strategija po kojoj prvo nešto okrenemo, a onda razdelimo. s druge obara strategija po kojoj prvo nešto okrenemo, a onda razdelimo.Ako od n novčića obrneš njih k, a potom ih razdeliš na dve gomile, tako da jednu čini p okrenutih i q neokrenutih, to je isto kao da si najpre podelio novčiće na dve grupe od po p+q i n-p-q novčića, a zatim u prvoj okrenuo p, a u drugoj k-p. Šta god uradio, na kraju ćeš imati dve gomile sa poznatim brojem novčića, pri čemu ćeš za svaku znati koliko je novčića u njoj okrenuto neparan broj puta. Sve transformacije se svode na to da si nešto okrenuo i da je na kraju sve podeljeno na dve gomile. Recimo da su u kovertama papiri na čijoj jednoj strani piše A, a na drugoj B. Koverte su numerisane brojevima od 1 do n. Imaš pravo da gledaš spolja, ali ne i da gledaš šta je unutra. Sve koverte su na početku okrenute na istu stranu i na početku ti je poznato koliko je papira u kovertama okrenuto stranom A na gore. To je ekivivalentna formulacija. Opšta transformacija se svodi na jednu particiju skupa {1,...,n} (podela na gomile) i jedan podskup skupa {1,...,n} (okrenute koverte u toj transformaciji). Kompozicija takvih transformacija je ponovo transformacija tog oblika. Važno je primetiti da prilikom prepaticionisanja koverti nije bitno koja je koverta bila na kojoj gomili, jer su sve koverte numerisane. Neka na kraju imam dve gomile, prvu sa m koverti, a drugu sa 100-m koverti. Ukoliko sam u prvoj prevrnuo q koverti (od kojih je 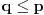 A-ovaca), a u drugoj t koverti (od kojih je [tes]s\leq t[/tex] A-ovaca), onda imamo A-ovaca), a u drugoj t koverti (od kojih je [tes]s\leq t[/tex] A-ovaca), onda imamoU prvoj gomili p prevrnutih A-ovaca, q-p prevrnutih B-ovaca, r neprevrnutih A-ovaca ( 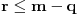 ), ),m-q-r neprevrnutih B-ovaca U drugoj gomili: s prevrnutih A-ovaca, t-s prevrnutih B-ovaca, 10-p-r-s neprevrnutih A-ovaca, 100-m-t neprevrnutih B-ovaca. Uslov da nakon toga na obe gomile imamo podjednako koverti sa papirom okrenutim A stranom na gore se svodi na q-p+r=10+t-p-r-2s, odnosno 2(r+s)=10+t-q. Veličine m, t i q su na m poznate, pa nam je poznata i desna strana jednakosti. Stoga leva strana jednakosti pri tako izabranim m, t, q ne sme zavisiti od r i s, koji su nam nepoznati, ali za koje znamo da r ne može biti veće od m-q i da s ne može biti veće od t. Jedina mogućnost da leva strana ime jednoznačno određenu vrednost je da bude iznuđeno r=s=0, odnosno da bude m=q i t=0, to jest, da smo u prvoj gomili prevrnuli sve koverte, a u drugoj nijednu. No tada je 0=2(r+s)=10+t-q=10-q, Odnosno q=m=10, a to je upravo Bojanovo rešenje prethodnog slučaja. [ Bojan Basic @ 05.10.2007. 15:08 ] @
[ galet@world @ 30.10.2007. 15:10 ] @
Konstruiši pravougli trougao ako je data dužina hipotenuze i tačka kroz koju treba proći
hipotenuza. Ta tačka nije na simetrali pravog ugla. Copyright (C) 2001-2024 by www.elitesecurity.org. All rights reserved.
|