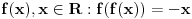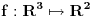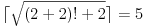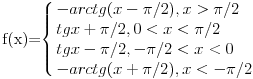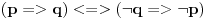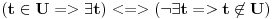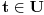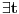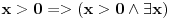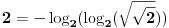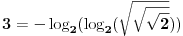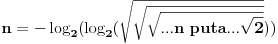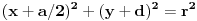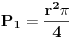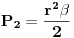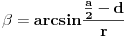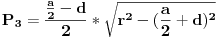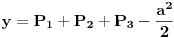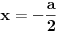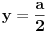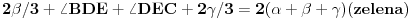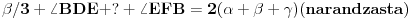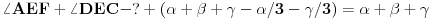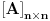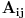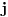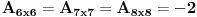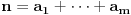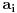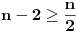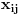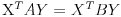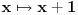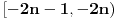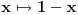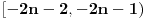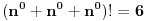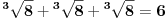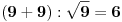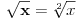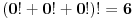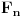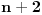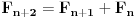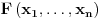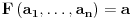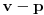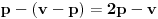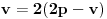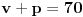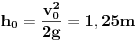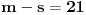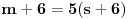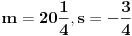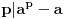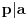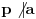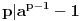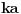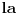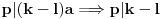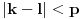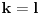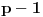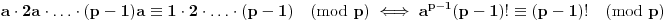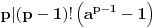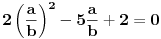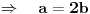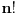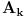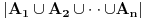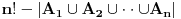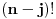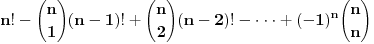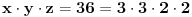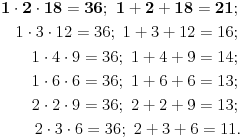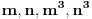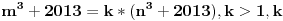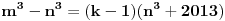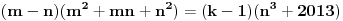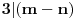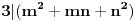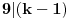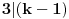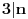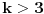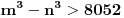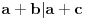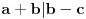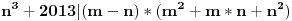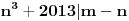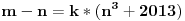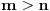|
|
[ Bojan Basic @ 29.08.2003. 17:56 ] @
|
| Ova tema je jednom bila na ES-u, ali je izgubljena prilikom havarije. Naime radi se o tome da svako napiše zadatke koje smatra najlepšim. Ne mislim na strogo matematičke zadatke u kojima treba lepa ideja, već na one koji na prvi pogled izgledaju apsolutno apsurdni, kao što će se videti iz primera. Ali prvo da ustanovimo neka pravila za pisanje u ovoj temi:
- Iako to ne služi za ovo, code tagovi imaju slabu primenu u matematičkom forumu, pa koristite njih da bi postovali nov zadatak, kako bi se izdvajao od rešenja i komentara posetilaca. Na početku obavezno naznačite redni broj zadatka od početka ove teme. Sve ovo doprinosi preglednosti i lakšem snalaženju. Evo prvih nekoliko priloga od mene:
- Ovo je po meni ubedljivo najlepši zadatak, neprevaziđen:
Code:
Zadatak 1:
Osoba A ima tri brata: osobe B, C i D, i nema više braće ni sestara. Svih četvoro
žive u istoj ulici. Osoba A živi u kući koja ima 3 prozora i 2 vrata. Osoba B ima
onoliko prozora koliko osoba C ima vrata, i osoba B ima onoliko vrata koliko osoba C
ima prozora. Osoba D ima onoliko prozora koliko iznosi zbir svih prozora njegove
braće, i onoliko vrata koliko iznosi zbir svih vrata njegove braće, i pri tome osoba D
ima jednak broj vrata i prozora. Da li tašta osobe A živi u toj ulici?
- Ovaj je sličan, samo daleko lakši:
Code:
Zadatak 2:
Slavko sa sinom i Jordan sa sinom bili su na pecanju. Slavko je upecao onoliko riba
koliko je upecao i njegov sin, a Jordan - tri puta više od svog sina. Ukupno su
upecali 35 riba. Sin Slavka se zove Nikola. Kako se zove Jordanov sin?
- Ovaj zahteva nešto veće poznavanje matematike:
Code:
Zadatak 3:
Predstaviti sve prirodne brojeve koristeći samo tri puta cifru 2 i matematičke
operatore.
- O ovom zadatku je diskutovano već dva puta na http://www.elitesecurity.org/tema/18994 i http://www.elitesecurity.org/tema/28130 , ali ga navodim samo da bi se nalazio u ovoj grupi:
Code:
Zadatak 4:
Gospodin Proizvod predstavlja proizvod dva prirodna broja između 2 i 200, a
Gospodim Suma njihovu sumu. Oni vode ovakav razgovor:
- Gospodin Proizvod: Ja ne znam o koja dva broja se radi.
- Gospodim Suma: Već sam znao da ne znaš!
- Gospodin Proizvod: Sada ja znam!
- Gospodim Suma: Sada i ja znam!!
Koji su to brojevi?
- Još samo jedan za sada, preuzet sa http://www.elitesecurity.org/tema/28002 :
Code:
Zadatak 5:
Nalazite se u sobi sa 3 prekidača. U drugoj sobi se nalaze 3 sijalice. Zna se da
svaki prekidač pali tačno jednu sijalicu, i da je svaku sijalicu moguće upaliti nekim
prekidačem. Smete da iskoristite prekidače, a zatim samo jednom da uđete u sobu
sa sijalicama, i odredite koji prekidač pali koju.
Ako nađem još neki, postovaću ga ovde. Nadam se da ima još ljudi koji će podržati moju ideju. |
[ stalker @ 30.08.2003. 19:13 ] @
Ovo je uzeto sa http://www.elitesecurity.org/poruka/86387
Code:
Zadatak 6:
Jedna ekspedicija je krenula iz svoje baze prema jugu. Nakon 10km je stala,
postavila znak i krenula ka istoku. Nakon 10km je videla jednog medu, pa je krenula
ka bazi i nakon 10km pesacenja vratila se u svoju bazu.
E sad pitanje glasi: Koje je boje bio medved?
Ovo ga i jedan moj lak:
Code:
Zadatak 7:
Na deset gomila imamo po 10 zlatnika i na svim gomilama su zlatnici teski 10g,
osim na jednoj na kojoj su teski 9g.Treba naci koja je to gomila koristeci samo
jedno merenje na digitalnoj vagi (ima jedan tas i ispisuje tacnu tezinu)
Jel moze resenje za 1. i 3. zadatak? [ Bojan Basic @ 30.08.2003. 19:55 ] @
Prvi zadatak mi se jako sviđa, i drugi je lep ali ga znam od ranije. Ne bih još da postujem rešenja zadataka, neka korisnici pokušaju sami da ih reše, pa ako niko ne uspe, onda ću dati pomoć. Drago mi je da se neko javio i da podržava moju ideju. Nadam se da će biti još puno ovakvih zadataka.
[ chupcko @ 01.09.2003. 08:32 ] @
Skoro su svi zadaci vec vidjeni (bar za mene) osim onog sa tri dvojke :), mada kada malo bolje razmislim sigurno i tu ima neki log(log(log(log(...)))
Moracu da razmislim, super, nazjad zadatak koji nisam nikada video :))).
[ filmil @ 01.09.2003. 08:53 ] @
Citat: Zadatak 8:
Naći 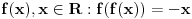
[ Ovu poruku je menjao Bojan Basic dana 05.09.2003. u 20:49 GMT]
[ Ovu poruku je menjao Bojan Basic dana 05.09.2003. u 20:49 GMT] [ srki @ 01.09.2003. 10:10 ] @
Citat: Bojan Basic:
Prvi zadatak mi se jako sviđa
Ali nije tezak.
Mada odgovor moze da bude i da stanuje u ulici i da ne stanuje. Ako je p pretpostavka i s posledica onda ako je p neT, s moze da bude i T i neT da bi "p sledi s" bilo ekvivalentno sa T.
Nagradno pitanje je sta je p :-)
a s nam je to da stanuje u istoj ulici pa zato moze biti i tacno i ne tacno jer je p netacno.
(Ne znam u Tex-u kako da stavim tu ekvivalenciju, implikaciju i T i neT)
[ stalker @ 01.09.2003. 11:48 ] @
Koliko sam ja skapirao prvi zadatak,osoba A je zensko=>nema tastu,jer je zbir prozora kao i vrata osobe D jednak zbiru njene BRACE=>nema nikakve gungule oko tautologija itd.
Citat:
Skoro su svi zadaci vec vidjeni (bar za mene) osim onog sa tri dvojke :), mada kada malo bolje razmislim sigurno i tu ima neki log(log(log(log(...)))
Dobra ideja,samo ne moze log(log(log(...))).Mozda bi moglo log(|log(|...|)) ili nesto kao log|(1/log(...)),a moze i e^e^...Samo pitanje ostaje da li sme da se koristi log(on mora da ima osnovu npr. 10 a taj broj ne sme da se koristi) i da li sme ln i e(oba koriste e a takodje ni to ne moze da se koristi?),a ako nastavimo tako ni 1/x ili 1/2 nije dozvoljeno jer je to 2^(-1),a -1 ne moze da se koristi.
Dakle,pitanje za Bojana-sta je sa ovim slucajevima? [ chupcko @ 01.09.2003. 15:49 ] @
Pa koliko mi mozak dopusta da sada razmisljam, ima negde ln i exp :)
doduse exp vec ima u sebi broj, to jest nije bas jasno definisano...
Ali eto, cim dodjem kuci i nemam pametnijih posla (a necu imati) mozda nesto uradim :).
A onaj f(f(x))=-x je zanimljiv, bese dejanova pitalica iz galaksije :))))
Mislim da sam bas tim zadatkom dobio jednogodsinju pretplatu svojedobno :), ili nisam :).
Hint za f(f(x)) ... je da se segment (0,1] preslika u (-inf,-1) ... i ostali sektori tamo gde im je mesto :))).
Bila je neka kobasica koja je koristila abs i sign :)
[ srki @ 01.09.2003. 21:17 ] @
Citat: stalker:
Koliko sam ja skapirao prvi zadatak,osoba A je zensko=>nema tastu,jer je zbir prozora kao i vrata osobe D jednak zbiru njene BRACE=>nema nikakve gungule oko tautologija itd.
Pa pitanje nije bilo da li osoba A ima tastu. Pitanje je bilo da li tasta osobe A stanuje u istoj ulici i onda je na ti pitanje potpuno ispravno odgovoriti i da i ne.
Ako pretpostavka p znaci da osoba ima tastu i to je netacno onda da bi p=>s bilo tacno s moze da bude i T i neT.
Ako je s znaci da tasta stanuje u istoj ulici onda moze da bude i tacno i netacno jer je p netacno. [ IronTIRANIN @ 02.09.2003. 07:48 ] @
Pogledao sam sve ove zadatke i mislim da imam resenja za 1,2,5,6 i 7.
[ darkosos @ 02.09.2003. 08:03 ] @
Ako se dobro secam, sa jednog pismenog iz analize 2:
Citat: Zadatak 9:
Ako je proizvoljna funkcija
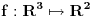
diferencijabilna, dokazati da nije 1-1.
[mod: TeX]
[ Ovu poruku je menjao filmil dana 03.09.2003. u 22:48 GMT]
[ Ovu poruku je menjao darkosos dana 04.09.2003. u 13:37 GMT]
[ Ovu poruku je menjao Bojan Basic dana 05.09.2003. u 20:51 GMT] [ IronTIRANIN @ 02.09.2003. 08:28 ] @
Odgovor na 1. zadatak
Neka je br.prozora na kuci osobe C x, a br.vrata y. Tada je br.vrata na kuci osobe B x, a br.prozora y. Po predpostavci zadatka sledi :
3+y+x=2+x+y, a to je nemoguce jer je 2<>3.
Tako da ne vidim kako se tasta uklapa u sve ovo ...
[ IronTIRANIN @ 02.09.2003. 08:31 ] @
Odgovor na 2. zadatak
Jordanov sin se zove Slavko. U pitanju su 3 osobe. Jordan je Slavkov otac a Nikolin deda. Sto se tice riba, Jordan je ulovio 21, Slavko i Nikola po 7.
[ IronTIRANIN @ 02.09.2003. 08:37 ] @
Odgovor na 3. zadatak
Sto se tice ovog problema, mislim da nesto ne stima u postavci. Ne mozemo predstaviti sve prirodne brojeve pomocu 3 dvojke. Najveci prirodan broj koji se moze napisati na ovaj nacin je 16! tj. (2^2*2)! . Ali nije to sve. Kada sam pokusao da proverim resenja u intervalu od 0 do 16!, nisam dobio resenja za sve brojeve. Npr. za broj 5, koji se nikako ne moze predstaviti pomocu 3 dvojke.
[ IronTIRANIN @ 02.09.2003. 08:42 ] @
Odgovor na 5. zadatak
Ovde nisam siguran u cemu je stos, ali moram da se slozim sa kolegom koji je imao ideju da prvo ukljucimo prvi prekidac, posle 10min da ga iskljucimo, zatim da ukljucimo drugi i da odmah upadnemo u sobu.
Sijalicu koja svetli u trenutku kada smo usli u sobu pali drugi prekidac. Sijalicu koja je topla pali prvi prekidac, a sijalicu koja je hladna treci.
[ IronTIRANIN @ 02.09.2003. 08:45 ] @
Odgovori na 6.i 7. zadatak
Ove odgovore mogu da ti posaljem mailom (mislim na moderatora), jer su resenja graficka, a ne pada mi na pamet da ih objasnjavam pismeno jer bi to bila poooduza poruka ...
[ srki @ 02.09.2003. 09:58 ] @
Citat: filmil:
Citat:
Naći 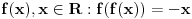
Zadatak ima beskonacno mnogo resenja:
Ajde ja cu da vam dam neki hint:
Probajte recimo da domen [0,Pi/2) preslikate na [1,+oo) pa [1,+oo) na (-Pi/2,0] a slicno tako preslikavamo i negativan domen. Recimo domen [0,1) mozete preslikati na [1,+00) sa 1+arctg(x) a [1,+oo) moze da se preslika sa -tg(x-1) na (-Pi/2,0] i tako dalje slicno se odradi za ostali deo domena.
A mi mozemo da razvlacimo te funkcije na x*Pi pa zato ima beskonacno mnogo resenja. A moze da se resava i sa logaritmima jer to preslikava domen (0,1] na (-oo,0]
A kada ne bi bilo ogranicenja da x pripada R onda bi najlakse resenje bilo ovo:
f(x)=x*i
[ stalker @ 02.09.2003. 13:48 ] @
Jos jednom pitanje za Bojana(3.zadatak):Jel sme da se koristi e,pi,log(i sa kojom osnovom)?Ili ovo nema veze sa resenjem...
P.S.Samo se nadam da nije neka mutljavina sa binarnim ili sistemom 3
[ chupcko @ 03.09.2003. 08:27 ] @
Citat: IronTIRANIN:
Odgovor na 3. zadatak
Sto se tice ovog problema, mislim da nesto ne stima u postavci. Ne mozemo predstaviti sve prirodne brojeve pomocu 3 dvojke. Najveci prirodan broj koji se moze napisati na ovaj nacin je 16! tj. (2^2*2)! . Ali nije to sve. Kada sam pokusao da proverim resenja u intervalu od 0 do 16!, nisam dobio resenja za sve brojeve. Npr. za broj 5, koji se nikako ne moze predstaviti pomocu 3 dvojke.
eh :), a sta mislis o ovome: ((((((((((2+2+2)!)!)!)!)!)!)!)!)!)!
Mislim da je ovaj broj punoooooooooooooo veci od 16!
Ajde da demantujemo jos nesto :)
ceil(sqrt((2+2)!+2))=ceil(sqrt(26))=ceil(5.099...)=5
Mozda nije cisto ali je tacno :)
Fora je sto sam se setio odakle znam resenje, to je matematicki vesnik iz 85/86 godine, ali igrom slucaja nemam ga vise :).
Tu je bio to zadatak meseca. [ IronTIRANIN @ 03.09.2003. 09:13 ] @
Citat: Ajde da demantujemo jos nesto :)
ceil(sqrt((2+2)!+2))=ceil(sqrt(26))=ceil(5.099...)=5
Mozda nije cisto ali je tacno :)
Ne naravno da nije cisto! Mislim da se ovde trazi matematicki dokaz, a ti primenjujes programiranje! Ruku na srce, u pravu si, ali ako resavas problem : SAP koji racuna broj 5 pomocu 3 dvojke.[ chupcko @ 03.09.2003. 11:40 ] @
eh, ceil je funkcija koja postoji u matematici i zove se celobrojni deo, oznaka je :
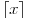
Koristi se na puno mesta bas, a cim postoji delimiter u obicnom TeX-u za to, eto jos jednog dokaza da postoji i u matematici :))).
Eto ajde da napisemo u tex-u (puno je vremena proslo):
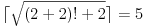 [ IronTIRANIN @ 03.09.2003. 20:34 ] @
U redu chupcko, predajem se!
Ali pazi sad ovo : 2+2+2=8 , a kako bi recimo napisao 7 i 9 ?
[ chupcko @ 04.09.2003. 08:14 ] @
Uf, sada sam se setio da u peanovoj aritmetici postoji funkcija succ (successors) koja je poznatija iz c-a kao ++ :))))
obicno se pise s(x) (mi kazemo sledbenik od x)
dakle ajde da probam s(s(s(s(s(2+2-2)))))=7 :))))
ma fora je naci kako se s(x) izrazava koristeci samo funkcije, to jest bilo je nesto ali nikako da se setim kako ide tacno, ako nema iko matematicki list kod kuce, neka pregleda 84-87 godiste :).
[ IronTIRANIN @ 04.09.2003. 20:59 ] @
Mislim da si upravo resio zadatak Chupcko.
Jer :
1=2-2/2, 2=2-2+2, 3=succ(2-2+2), 4=succ(succ(2-2+2)), ...
Dakle, kako se povecava broj levo od zagrade, tako dodajemo jedno succ(...). To bi terbalo da bude onda resenje zadatka, zar ne?
[Ovu poruku je menjao Bojan Basic dana 05.09.2003. u 20:52 GMT]
[ darkosos @ 05.09.2003. 07:21 ] @
Nisam siguran da je to ono na sta se misli u ovom zadatku. Ovako je dovoljno da dobijemo 1, a onda dodajemo succ. Nema smisla, jer je jednako kao da se trazi da se 1 napise pomocu 3 dvojke. Sto ne onda dve dvojke (2:2) ili cetiri (2+2):(2+2) itd..., moze i sa bilo kojim drugim brojevima.
[ Bojan Basic @ 05.09.2003. 18:24 ] @
Što se tiče trećeg zadatka, smeš da koristiš SVE matematičke operatore, ali cifru 2 smeš napisati samo tri puta, i ne smeš napisati nijednu drugu cifru. Dozvoljeno je napisati, na primer, logaritam sa osnovom dva, ali tu imaš upotrebljenu već jednu dvojku (i ona se računa). Naravno, rešenje upotrebom succ nije korektno, jer to nije neka od redovnih funkcija.
[ stalker @ 07.09.2003. 10:04 ] @
Dakle evo mog resenja.
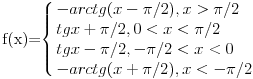
Nadam se da valja.Moram reci da mi nijedan zadatak ni iz jednog predmeta nije bio tezak kao ovaj ("bio" pod uslovom da je ovo tacno).Inace,bilo ovo tacno ili ne-ima jako lep grafik.
Dalje,za one 3 dvojke-tu je neka prevara.Razmisljao sam puno(dobro,ne bas danonocno),ali to je neka teska prevara.
Posto vidim da je ovde nesto zamrlo sa dodavanjem novih zadataka,evo jednog iz Dejanovih pitalica,Racunari br. x (90<x<110)
Code:
Zadatak 10:
Jedan bazen se napuni za 5h(kada se samo puni),a isprazni za 10h
(kada se samo prazni).Koliko je potrebno vremena da se bazen napuni
kada radi ta ista slavina za punjenje i otvoren je taj
isti ventil za praznjenje.
Da,ne ponosim se bas sobom sto sam stavio ovaj zadatak,jer ovo trebaju,koliko sam ja razumeo da budu logicki,a ovako prelazi tema u teske mat. zadatke.Ali,neko mora da pokrene...
[ Ovu poruku je menjao Bojan Basic dana 07.09.2003. u 12:45 GMT] [ filmil @ 07.09.2003. 10:29 ] @
Citat: stalker:
pitalica,Racunari br. x (90<x<110)
Upravo tako, u pitanju su računari br. 100, ali mislim da je bazen već suviše složen, pogotovo što i nije u pitanju čista matematika.
f
[ srki @ 07.09.2003. 12:24 ] @
Citat: Bojan Basic:
Naravno, rešenje upotrebom succ nije korektno, jer to nije neka od redovnih funkcija.
Pa dobro, succ moze lako da se zaobidje koriscenjem ln i e^x ali ne znam da li je to dozvoljeno. Ako jeste onda je zadatak lak i ne znam sta ce nam treca dvojka.
[ Bojan Basic @ 07.09.2003. 14:48 ] @
Nisam baš najjasnije postavio zadatak, pa da sumiramo:
- Sme se koristiti:
1) cifra 2 (tri puta)
2) svi matematički operatori i funkcije (naravno, one "normalne", ne succ i slično)
- Sve ostalo (uključujući i konstante  ... nije dozvoljeno.
[ BOOK @ 07.09.2003. 23:27 ] @
Citat: IronTIRANIN:
Odgovor na 1. zadatak
Neka je br.prozora na kuci osobe C x, a br.vrata y. Tada je br.vrata na kuci osobe B x, a br.prozora y. Po predpostavci zadatka sledi :
3+y+x=2+x+y, a to je nemoguce jer je 2<>3.
Tako da ne vidim kako se tasta uklapa u sve ovo ...
Tvoja logika ima rupa. Na primer, sta kazes na ideju da A i B stanuju zajedno u jednoj kuci 2/3 (vrata/prozori), osoba C u kuci 3/2, a osoba D u kuci 5/5 ??
Ovo je ujedno i postavka stanja koja zadovoljava sve uslove zadatka, a iz koje se ne moze zakljuciti da li tasta zivi u istoj ulici ili ne. Dakle, zadatak nije sasvim korektan, odnosno mogu odgovoriti na postavljeno pitanje: It cannot be determined from the information given.
Mozda je trebalo da se postavi pitanje: "Kakva treba da bude situacija (npr. pol muski/zenski, zajednicke kuce ili najverovatnije neka treca fora) da bi se moglo zakljuciti da li tasta zivi ili ne?". [ chupcko @ 08.09.2003. 08:46 ] @
Citat: Bojan Basic:
Što se tiče trećeg zadatka, smeš da koristiš SVE matematičke operatore, ali cifru 2 smeš napisati samo tri puta, i ne smeš napisati nijednu drugu cifru. Dozvoljeno je napisati, na primer, logaritam sa osnovom dva, ali tu imaš upotrebljenu već jednu dvojku (i ona se računa). Naravno, rešenje upotrebom succ nije korektno, jer to nije neka od redovnih funkcija.
Eh ovo je sada malo preciznija formulacija, doduse ne bi se slozio sa time da je succ neredovna funkcija, cim je jedna od osnovnih opisanih u peanovoj aritmerici :))).
Ali eto sada znamo sta i kako, doduse ne bi bilo lose da se da spsak dozvoljenih funkcija. [ srki @ 08.09.2003. 12:44 ] @
pa i succ mozes da napravis kao +x/x ili + e^x/e^x ili +x!/x! ili na bilo koji nacin dobijemo jedinicu pa samo dodajemo koliko nam treba. pretpostavljam da to ne moze pa da li bi ipak mogla preciznija formulacija zadatka.
zasto ne bi moglo recimo succ(x) da se uradi kao ln(e*e^x)? da li bi to bilo dobro resenje ili ipak ne sme "e" da se koristi jer to nije operator.
i sta ti znace redovne funkcije? zasto succ nije redovna?
da li su dozvoljene samo elementarne funkcije ili sta? mada succ jeste elementarna jer moze da se dobije preko drugih elementarnih.
da li mozes da ostavis link sa spiskom redovnih funkcija. priznajem da mi taj pojam nije poznat.
[ chupcko @ 08.09.2003. 13:05 ] @
E ovako je krenulo 1900-te na onom kongresu matematicara (kada je cika Hilbert izlozio gomilu zadataka), bese desti Hilbertovi problem spominjao pojam : "efektivno izarcunljivo", pa su se kasnije ljudi lomili da formalizuju taj pojam, naravno sada se najvise spominju rekurzivne funkcije, URM, postove zamene i naravno turingova masina :))).
Dakle da bi zadatak bio dobar bilo bi lepo dati spisak funkcija koje smemo da koristimo jer ova succ je definitno rekurzivna (vise nego ocigledno ...) pa samim tim je i intuitvno izarcunljiva pa i "redovna" :)))
(vidi tezu Churcha za detalje).
Dakle dok ne dobijemo tacan spisak funkcija/operacija koje smemo da koristimo u zadatku.
[ IronTIRANIN @ 11.09.2003. 17:03 ] @
Citat: stalker
Zadatak 10:
Jedan bazen se napuni za 5h(kada se samo puni),a isprazni za 10h
(kada se samo prazni).Koliko je potrebno vremena da se bazen napuni
kada radi ta ista slavina za punjenje i otvoren je taj
isti ventil za praznjenje.
Ne bih da se pravim pametan, ali zadatak je veoma lak i resava se sablonski.
Za 1h napuni sa 1/5 bazena a isprazni 1/10. Kada su otvorene obe slavine, za 1h napuni se dakle 1/5 - 1/10 = 1/10 deo bazena. Odavde sledi da se bazen puni za 10h po uslovu zadatka . [ stalker @ 11.09.2003. 18:19 ] @
Citat: Ne bih da se pravim pametan, ali zadatak je veoma lak i resava se sablonski.
Za 1h napuni sa 1/5 bazena a isprazni 1/10. Kada su otvorene obe slavine, za 1h napuni se dakle 1/5 - 1/10 = 1/10 deo bazena. Odavde sledi da se bazen puni za 10h po uslovu zadatka .
Neko je naseo!!!(Salim se naravno)
Inace u Racunarima 100 se kaze posle pitanja da resenje nije ovo gore citirano(namerno to nisam dodao),moraces malo da uracunas i brzinu isticanja vode.Posto je presek bazena konstantan za sve visine( tj. povrsina istog) mozes da koristis Toricelijevu teoremuVisticanja=sqrt(2gh).Eto mala pomoc [ Bojan Basic @ 13.09.2003. 12:03 ] @
Pa kad ste baš navalili.
U rešenju koje ja imam koristi se samo ideja koja kombinuje log i koren. Eto, neka vam to bude i mala pomoć. A ako neko nađe neko drugo rešenje, neka ga objavi ovde. Pošto ste svi zapeli šta su to reedovne funkcije, mislio sam da znate na šte mislim, ali prevario sam se. Pa dobro, neka bude ovako: rešenje sa succ jeste korektno, ali je suviše nekako prozaično, i svako može da zaključi da "to nije to" (kao što je dobro primetio darkosos).
A što se tiče onoga što je BOOK zapazio u vezi prvog zadatka, moram da priznam da se toga ne bih setio. Rešenje koje sam ja imao u vidu je ono koje je predložio stalker, i nije mi bila jasna srkijeva primedba:
Citat: srki:
Pa pitanje nije bilo da li osoba A ima tastu. Pitanje je bilo da li tasta osobe A stanuje u istoj ulici...
Pa logično je da ako osoba A nema taštu, da njena tašta ne živi nigde, pa ni u toj ulici, ili grešim?!
Da se vratim na BOOK-ovu primedbu. Zahvaljujući tome dobijamo sasvim nov zadatak, koji je već rešen, ali evo njegovog teksta.
Code:
Zadatak 1':
Osoba A ima tri brata: osobe B, C i D, i nema više braće ni sestara. Svih četvoro
žive u istoj ulici. Osoba A živi u kući koja ima 3 prozora i 2 vrata. Osoba B ima
onoliko prozora koliko osoba C ima vrata, i osoba B ima onoliko vrata koliko osoba C
ima prozora. Osoba D ima onoliko prozora koliko iznosi zbir svih prozora njegove
braće, i onoliko vrata koliko iznosi zbir svih vrata njegove braće, i pri tome osoba D
ima jednak broj vrata i prozora. Naći broj prozora i vrata osobe D, ako se zna da i
tašta osobe A živi u toj ulici. [ srki @ 13.09.2003. 13:30 ] @
Citat: Bojan Basic:
Citat: srki:
Pa pitanje nije bilo da li osoba A ima tastu. Pitanje je bilo da li tasta osobe A stanuje u istoj ulici...
Pa logično je da ako osoba A nema taštu, da njena tašta ne živi nigde, pa ni u toj ulici, ili grešim?!
Pa isto bi bio tacan odgovor i da kazes da njena tasta stanuje svuda jer ne postoji njena tasta pa je bilo sta sto se odnosi na pogresnu pretpostavku tacno.
Iz pogresne pretpostavke mozes da zakljucis bilo sta. Recimo ako pretpostavis da je 1=2 iz toga mozes da zakljucis i da je 2=3 ili recimo 1=4 itd...
Znaci ako je pretpostavka da osoba A ima tastu pogresna onda iz toga mozes da zakljucis sta hoces pa i da je zemlja ravna.
Znaci (p => q) <=> T ako je p false.
odnosno ako je p false q moze da bude bilo sta pa moze da bude i true i false. Ako nama p znaci da osoba A ima tastu a q nam znaci da tasta stanuje u istoj ulici onda posto je p false iz toga mozemo da zakljucimo sta hocemo za q.
Znaci na zadatak smo slobodno mogli i da odgovorimo bilo sta jer nije lepo postavljen.
Evo ti npr. sledeci zadatak: broj x je veci za jedan od broja y. broj z je jednak broju x a takodje je jednak i broju y.
Da li je x=y?
E tu mozes da odgovoris sta hoces jer je pogresna pretpostavka da postoje takvi brojevi. Isprabno pitanje je da li skup resenja (x,y,z) prazan ili tako neko.
[ Bojan Basic @ 13.09.2003. 14:25 ] @
Srki, nisi u pravu.
Zakon kontrapozicije kaže:
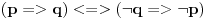
Konkretna pretpostavka je:
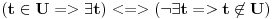
Pošto je prva pretpostavka očigledno tačna, mora biti tačna i druga. A pogledaj šta je druga pretpostavka u našem zadatku:
ne postoji tašta=>tašta ne živi u ulici [ srki @ 13.09.2003. 16:00 ] @
Citat:
Konkretna pretpostavka je:
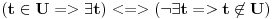
E, pa necemo tako :-) Izgleda da mislimo na razlicite stvari o tome sta nam predstavlja pretpostavku.
Pocetna pretpostavka nije 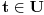 niti onaj izraz vec je po zadatku pocetna pretpostavka 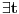 .
A posto pocetna pretpostavka nije tazna onda iz toga ne mozemo da zakljucimo nista pa posledica moze da bude bilo sta. Znaci bilo koji odgovor je tacan.
Pitanje u zadatku je lose i zato je moguce dati bilo kakav odgovor.
Evo, resi sledeci zadatak. Da li je resenje (po x) sledeceg sistema pozitivno ili negativno:
{x+y=1 , x+y=3}
Odgovor bi bio da sistem nema resenja ali to nije bilo pitanje. Odgovor na ono pitanje moze da bude i da je x manje od nule i da x nije manje od nule jer je pretpostavka da x postoji pogresna.
Pazi ako je pitanje samo da li je x vece od nule po tvom primeru ti bi odgovorio ne a koliko ja znam negacoja od X>0 je X<=0 a to opet nije tacno jer x ne postoji.
Znaci ako je pitanje lose postavljeno onda mozemo slobodno odgovoriti kako hocemo. Pravilno pitanje bi glasilo da li osoba A ima tastu.
[ Bojan Basic @ 13.09.2003. 17:23 ] @
Srki, ti jednostavno previše želiš da isfilozofiraš nešto čega nema. Na tvoje pitanje da li je x>0, ja bih ti naravno rekao ne.
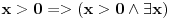
Sada primeni De Morganov zakon:

Vidiš li na čega se svodi "x nije veće od nule"?
Shvatam šta hoćeš da kažeš, ali razmisli malo, ipak preteruješ. Pa kad te neko na ulici pita: "Imaš li sat?", da li mu kažeš: "Imam", ili mu kažeš koliko je sati?
[ Ovu poruku je menjao Bojan Basic dana 20.09.2003. u 15:47 GMT] [ srki @ 13.09.2003. 17:35 ] @
Citat: Bojan Basic:
Srki, ti jednostavno previše želiš da isfilozofiraš nešto čega nema.
:-)
Citat: Shvatam šta hoćeš da kažeš, ali razmisli malo, ipak preteruješ. Pa kad te neko na ulici pita: "Imaš li sat?", da li mu kažeš: "Imam", ili mu kažeš koliko je sati?
Ubedio si me, stidim se :-)))
pozdrav
[ BOOK @ 13.09.2003. 18:22 ] @
Citat: srki:
Pravilno pitanje bi glasilo da li osoba A ima tastu.
Nije ni to pravilno pitanje (vidi gore). [ Bojan Basic @ 13.09.2003. 19:29 ] @
Pa dobro, BOOK, već sam ti rekao da nisam ni pomislio na ono što si ti rekao, i da bi se to zaobišlo, u postavci zadatka mora još stajati da svako ima svoju kuću (ili izmeniti pitanje kao što sam napisao u Zadatku 1'). Inače, ja ostajem pri svom pitanju, jer je više snebapaurebrastije.
[ BOOK @ 14.09.2003. 00:50 ] @
Citat: Bojan Basic:
Pa dobro, BOOK
OK, samo kazem srkiju da obrati paznju na moj post :)
Inace, sto se tice zadatka sa tri dvojke, sada je najzad sve jasno:

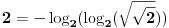
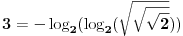
i uopste:
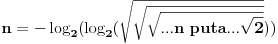 Moderator: tex
Moderator: tex[ Bojan Basic @ 14.09.2003. 11:03 ] @
Da, to je rešenje koje sam imao u vidu (samo sam ti stavio tex da izgleda lepše). Da li je ovo rešenje (pored onog sa succ) jedino ne znam, možda neko nađe još nekakvo.
[ chupcko @ 14.09.2003. 21:45 ] @
Daaaaaaaaa to je to resenje sa 3 dvojke :), steta sto sam ovih dana u muzici i mozak mi nije ni malo ukljucen, osim da brojim taktove :))).
[ stalker @ 14.09.2003. 23:02 ] @
Izvinjavam se,ja stvarno ne bih da budem cepidlaka,resenje je lepo(u matematickom smislu),ali zasto u logu ubacujemo dvojku,a u korenu ne.Mislim,ako cemo striktno?
[ BOOK @ 15.09.2003. 17:48 ] @
Da, ovo je i meni palo na pamet minut pošto sam došao do rešenja. Dato rešenje je čisto rezultat konvencije: dogovorili se ljudi da ako se drugačije ne napiše u levom gornjem uglu korena, koren smatramo kvadratnim. Međutim, eto, tako je kako je: nisam ja uveo tu konvenciju...  A u log-u ubacujemo dvojku zato što se podrazumeva da je log bez napisane osnove ustvari log osnove 10, a nama treba osnova 2  [ Bojan Basic @ 19.09.2003. 20:30 ] @
Ovo je "mojih ruku delo", a mislim da je stvarno dobro. Samo pažljivo pročitajte pitanje, da ne biste iz zaleta došli do rešenja koje se ne traži.
Code:
Zadatak 11:
Sveštenik i zvonar
Jednog letnjeg dana, baš kad je sunce počelo da peče,
u obližnjoj crkvi sveštenik zvonaru reče:
"U ponedeljak sretoh osobe tri,
nijednu od njih ne poznaješ ti.
Upitah ih za broj godina njihovih,
koje u zbiru daju dvostruki broj godina tvojih.
Pitanje koje ti postavljam nije lako,
odredi koliko je star od njih svako."
"Nemam dovoljno informacija, i provešću mnoge neprospavane noći,
možeš li mi bar malo pomoći?"
"Otvori uši i mozak uključi,
možda će ti ovo pomoći da rešiš problem koji te muči.
Uz sledeći podatak pokušaj da rešiš zadatak jednoznačno:
proizvod njihovih godina iznosi dve hiljade četiri stotine pedeset tačno."
Nadam se da ti ne treba više pomagati,
očekujem da ćeš mi uskoro rešenje dati."
Zvonar je proveo noć bez sna,
pokušavajući da izračuna broj njihovih godina.
"Skoro sam našao odgovor tačan,
mada mi zadatak jop uvek ne izgleda jednoznačan."
"Još jednu pomoć ti dajem, a poštujem i stih,
stariji sam od sve trojice njih."
Kad je ovo čuo zvonar se nasmešio:
"Zazvonilo mi je uglavi, zadatak sam rešio!"
A ti, čitaoče koji ovo čitaš,
došlo je vreme da se pitaš.
Pitalica je ova vrlo fina,
nađi broj sveštenikovih godina! [ stalker @ 20.09.2003. 17:59 ] @
50,mozda
P.S.Los ti deseterac  [ zzzz @ 20.09.2003. 20:01 ] @
Treba li odgovor dati u stihovima?
Čije godine pogađamo:Za sve tri osobe,zvonara i popa?
Sve mi se čini da ti je kod pravljrnja stihova pomagao Kvazimodo.
[ BOOK @ 20.09.2003. 20:39 ] @
Pošto nigde u zadatku nisi rekao koliko čovek može da živi, a ja kao matematičar
ne smem da podrazumevam (skoro) ništa van onog što mi je dato, slede sve moguće neuređene trojke koje u proizvodu daju 2450, a predstavljaju godine onih troje ljudi:
Code:
(1,1,2450) = 2452
(1,2,1225) = 1228
(1,5,490) = 496
(1,7,350) = 358
(1,10,245) = 256
(1,14,175) = 190
(1,25,98) = 124
(1,35,70) = 106
(1,49,50) = 100
(2,5,245) = 252
(2,7,175) = 184
(2,25,49) = 76
(2,35,35) = 72
(5,5,98) = 108
(5,7,70) = 82
(5,10,49) = 64
(5,14,35) = 54
(7,7,50) = 64
(7,10,35) = 52
(7,14,25) = 46
Kao što primećujemo, desno od svake trojke prikazan je zbir članova te trojke. Da bi čika zvonar bio u nedoumici, zbir negde u gore navedenoj listi mora da se ponavlja. Zaista, jedini zbir koji se ponavlja je 64, pa se on dvoumi između trojki (5,10,49) i (7,7,50). Pošto se prestao dvoumiti kada je čuo da su sve tri osobe mlađe od sveštenika, zaključujem da sveštenik mora biti stariji od najstarijeg u jednom paru i mlađi od najstarijeg u onom drugom paru. Gledajući gore navedena dva para uviđamo da je sveštenik stariji od onog koji ima 49 godina, ali mlađi od onog koji ima 50 godina. Pošto se radnja priče dešava u dva dana jer je zvonar tražio celu noć one parove, zaključujem da je sveštenik u međuvremenu napunio 50 godina, jer je to jedini način da bude sigurno mlađi od onog koji je još "u ponedeljak" imao 50 godina. Dakle, sveštenik ima 50 godina.
Zvonar ima 32 godine (64:2), ali ne znam čemu to služi u zadatku. [ stalker @ 22.09.2003. 21:01 ] @
Nije nesto narocito,sam sam ga smisljao.Mislim da je zadatak dosta lak.
Code:
Zadatak 12

Prvo d treba gore,ne znam da ga postavim,neka moderator sredi to.Izvinjavam se...
Bojan Bašić: sređeno...
[Ovu poruku je menjao Bojan Basic dana 15.05.2005. u 19:49 GMT+1][ srki @ 23.09.2003. 11:53 ] @
Nula.
[ stalker @ 01.10.2003. 15:31 ] @
Znam da cu zazaliti zbog ovoga,ali neka ga...
Code:
Zadatak 13.
Dva brata Predrag i Nenad rodjeni su istog dana,
istog meseca,iste godine u isto vreme,
u istom mestu i od istih roditelja,ali nisu blizanci.Kako?
Ko zna nek ne postuje [ zzzz @ 01.10.2003. 23:20 ] @
Ja ne znam , dakle postuvatiću .Ovako:Da upitam-jel su imali još sestara , ili
braće?Ako nisu onda slijedi još pitanja.
[ stalker @ 02.10.2003. 19:23 ] @
Ima ( brace ili sestara)
[ srki @ 03.10.2003. 01:26 ] @
Pa znaci to je resenje :-)
[ chupcko @ 03.10.2003. 08:28 ] @
A jel Predrag i Nenad imaju isti genetski materijal ?
Mislim da znam resenje, ovo mi lici na Dejanove pitalice iz Galaksije :).
[ stalker @ 03.10.2003. 15:32 ] @
Citat:
Pa znaci to je resenje :-)
To je resenje:) Ukoliko mislis ono sto ja mislim...
Citat:
A jel Predrag i Nenad imaju isti genetski materijal ?
Pa valjda imaju
Citat:
Mislim da znam resenje, ovo mi lici na Dejanove pitalice iz Galaksije :).
Ne lici,ovo je mnogo bezazlenije i gluplje [ srki @ 03.10.2003. 15:35 ] @
Citat: stalker:
Citat:
Pa znaci to je resenje :-)
To je resenje:) Ukoliko mislis ono sto ja mislim...
:-)))
Stavio si resenje kao na tacni. Cudi me da i dalje ne provaljuju u cemu je fora :-)
[ chupcko @ 04.10.2003. 18:15 ] @
Pa dejanove pitalice (Q zadatak) je bio bas na tu foru, kao : covek nesto kupi i shvati da cim je kupio ne moze to da koristi (kupio je skup novcanik :))) )
Nisam siguran, ali mislim da je ovako nesto bili neka Q pitalica :).
Doduse ako nisu jednojacani blizanci ne mogu imati identican genetski materijal (jelte mogu cak biti i razlicitog pola :))) )
Doduse ne znam kolika je raspodela jednojajcanih cetvorki i trojki i ...
[ zzzz @ 05.10.2003. 00:08 ] @
Ovo je stvarno gadan zadatak.Nema šanse da neko pogodi
koliko ih je bilo , 3, 4, 5, ..
Ja ću probati skromno:trojke?
[ stalker @ 05.10.2003. 12:37 ] @
Skromno si i pogodio,mada mogu biti bilo sta(i cetvorke...)
[ roentgen @ 06.10.2003. 16:22 ] @
Evo ga resenje zadatka:
Pronaci sve funkcije y = f(x) koje zadovoljavaju f( f(x) ) = -x.
Postoje dva puta: geometrijsko resenje i analiticko resenje.
Za oba resenja je zgodno koristiti modifikovanu formu zadatka:
(1) f-1(x) = f(-x) <=> f( f(x) ) = -x.
Geometrijsko resenje:
Definisimo pomocnu funkciju
(2) g(x) = f(-x).
Na osnovu (1) vazi ce da je g(x) inverzna funkcija od f(x).
Geometrijski to znaci da je g(x) slika od f(x) u odnosu na osu simetrije y= x.
Opet na osnovu (2) vazi da je g(x) slika od f(x) u odnosu na osu simterije
x = 0 (apscisu).
Zakljucak: f(x) mora posedovati osobinu jedne slozene simetrije koja se
definise na sledeci nacin
Slika f(x) u odnosu na osu simterije y = x preslikana jos jednom u odnosu
na osu simetrije x = 0 mora biti jednaka samoj funkcija f(x).
Primer: Jednacina kruga x2 + y2 = r2 ispunjava taj uslov.
Na osnovu geometrijskog resenja se dolazi i do jedne teoreme znacajne za
analiticko resenje:
Teorema: Ako tacka (d,c) pripada trazenoj fukciji:
(3) c = f(d)
onda i tacka (-c,d) mora pripadati toj funkciji:
(4) d = f(-c).
Dokaz: Iz (3) sledi:
d = f-1(c)
a to kombinovano sa (1) daje direktno (4).
Analiticko resenje:
Primer sa krugom, jednom funkcijom u implicitnoj formi, pokazuje jedan put
moguce generalizacije
koristeci opstu implicitnu formu jedne realne funkcije y = f(x),
definisane
na ideji Taylorovog polinomialnog razvoja:
(5) a(0,0) + a(0,1)*y + a(1,0)*x + a(1,1)*x*y + a(1,2)*x*(y2) +
a(2,1)*(x2)*y + a(2,2)*(x2)*(y2) + .... = 0
Pri cemu su sve moguce funkcije definisane kroz razlicite setove
koeficijenata a(n,k) / {n,k} = 0,1,2,....
Ako se u pomoc prizove i malo matricnog racuna, jednacine se daju
elegantnije procesirati. Za to je dovoljno definisati
vektor:
(6) T{V[x]} = [1, x, x2, ...]
gde T{*} oznacava "transponovani" vektor ili matricu,
i matricu koeficijenata:
(7) A=
|a(0,0) a(0,1) .|
|a(1,0) a(1,1) .|
|. . . |
Od pomoci ce biti i jednostavna relacija:
(8) V[-x] = J x V[x],
gde je J dijagonalna matrica (svi elementi sem na glavnoj dijagonali su
nule) pri cemu se na glavnoj dijagonali
naizmenicno smenjuju: +1, -1, +1, ....
Matricno napisana opsta implicitna forma (5) glasi:
(9) T{V[x]} x A x V[y] = 0.
Na osnovu Teoreme ona mora istovremeno vaziti za tacku (d,c):
(10) T{V[d]} x A x V[c] = 0
i za tacku (-c,d):
(11) T{V[-c]} x A x V[d] = 0,
za proizvoljne realne brojeve "d" i "c". Uz pomoc osnovnog matricnog
racuna
i relacije (8) poslednja
jednacina se da modifikovati u jednu formu pogodnu za poredjenje sa (10):
(12) T{V[d]} x T{A} x J x V[c] = 0.
Posto (10) i (12) treba da vaze za bilo koju tacku (d,c), sledi uslov za
matricu koeficijenata:
(13) A = T{A} x J
Iz matricnog racuna ostaje da se dokazu sledeca pravila za
konstrukciju, na osnovu (13),
matrice koeficijenata opste implicitne forme funkcije (1):
- na svim pomocnim neparnim dijagonalama su svi koeficijenti nula;
- na glavnoj dijagonali su svi koeficijenti na neparnim pozicijama nula;
- na svim pomocnim parnim dijagonalama iznad glavne koeficijenti su
zavisni od koeficijenata na parnim dijagonalama ispod glavne na
simetricnim pozicijama:
. koeficijenti u parnim kolonoma iznad glavne dijagonale su jednaki
simetricnim koeficijentima ispod glavne dijagonale;
. koeficijenti u neparnim kolonoma iznad glavne dijagonale su jednaki
sa negativnim simetricnim koeficijentima ispod glavne dijagonale; i
. koeficijenti na parnim pomocnim dijagonalama ispod glavne kao i na
parnim pozicijama na glavnoj dijagonali su proizvoljni realni brojevi.
Primer: Za (n,k) = 0,1,2,3
A=
|a(0,0) 0 a(2,0) 0 |
|0 0 0 -a(3,1) |
|a(2,0) 0 a(2,2) 0 |
|0 a(3,1) 0 0 |
pri cemu su a(0,0), a(2,0), a(3,1) i a(2,2) proizvoljni realni brojevi.
Naprimer za: a(0,0) = -1 i a(2,0) = a(3,1) = a(2,2) = 1 dobija se funkcija
u
implicitnoj formi (5):
-1 + x2 + y2 + (x2)*(y2) + (x3)*y - x*(y3) = 0
koja zadovoljava uslov (1).
Dobijeno resenje se moze lako prosiriti i na kompleksne funkcije koristeci
Laurent-ov polinomijalni razvoj kompleksne funkcije
umesto Taylor-ovog razvoja realnih funkcija. Sa time se matrica A
produzuje
i na stranu negativnih indeksa (n,k) = ..., -1, 0, +1, ...
Tada su naravno i koeficijenti u matrici A kompleksni brojevi. Medjutim
pravila konstrukcije matrice A ostaju vrlo slicna.
[Ovu poruku je menjao roentgen dana 21.11.2003. u 02:29 GMT]
[ Bojan Basic @ 14.10.2003. 23:15 ] @
Samo ću malo da te dopunim:
Citat: roentgen:
Zakljucak: f(x) mora posedovati osobinu jedne slozene simetrije koja se
definise na sledeci nacin
Slika f(x) u odnosu na osu simterije y = x preslikana jos jednom u odnosu
na osu simetrije x = 0 mora biti jednaka samoj funkcija f(x).
Nije li jednostavnije da kažeš rotacijom oko koordinatnog početka za ugao 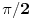 f se preslikava u samu sebe (pošto je kompozicija osnosimetričnog preslikavanja u odnosu na dve prave koje se seku pod uglom  rotacija oko tačke preseka za ugao od 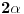 . U svakom slučaju, rešenje je korektno.
Evo još jednog zadatka od mene:
Code:
Zadak 14:
Jovan i Petar su rođeni u maju, jedan 1932. godine, a drugi 1933. U to vreme
satovi nisu bili tačni kao današnji, te od dva sata koje su imali jedan je svakog sata
kasnio za 10 sekundi, a drugi žurio za 10 sekundi. Jednog dana u januaru u podne,
Petar i Jovan su namestili satove na tačno vreme. "Vidiš", reče Petar Jovanu, "ovi
satovi će prvi put počevši od sada pokazati isto vreme tačno na tvoj 47.
rođendan". "U pravu si", reče Jovan. Ko je od njih dvojice stariji? [ zzzz @ 15.10.2003. 00:53 ] @
Jovan je stariji.(Petar je bio apostol a Jovan je krstio isusa pa na osnovu te logike
tako ispade).Ako nisam u pravu ajde dokaži .
[ Bojan Basic @ 15.10.2003. 10:37 ] @
Citat: zzzz:
Ako nisam u pravu ajde dokaži .
Vrlo jednostavan dokaz: Jovan i Petar o kojima ja pričam su rođeni 1932 i 1933. godine, a oni o kojima ti pričaš mnoooogo ranije.
[ BOOK @ 15.10.2003. 16:56 ] @
Pretpostaviću da se radi o satovima sa kazaljkama, a ne digitalcima koji idu od 00:00 do 23:59. Dakle, Petrov iskaz "ovi satovi će prvi put počevši od sada pokazati isto vreme" ću tumačiti da će nakon 12 sati razlike između vremena tih satova, oni pokazivati isto vreme.
Nakon jednog sata od trenutka nameštanja satova tog januarskog podneva, oni će se razlikovati za 10+10=20 sekundi, a tražena razlika od 12 sati biće nakon 12*60*60/20=2160 sati, odnosno 90 dana. Dakle, za 90 dana nakon "jednog januarskog popodneva" biće rođendan Jovanu, tj. biće "jedan dan u maju".
Očigledno je između jednog januarskog i jednog majskog dana mora proteći ceo februar, mart i april, tj. minimum punih 28+31+30=89 dana. Preostali 1 dan mora otići na jedan deo poslednjeg dana januara i jedan deo prvog dana maja. Dakle, nameštanje satova se odvija u podne 31. januara, a tačno 90 dana protiče 1. maja u 12 sati (tog dana je rođendan Jovanu).
Pošto se radi o 47-om rođendanu, kandidati za godinu kada su namestili satove su 1932+47=1979. godina i 1933+47=1980. godina. Sada dolazi ključna tačka: pažljivom čitaocu nije promaklo moje potajno podrazumevanje da februar ima 28 dana (kada sam sabirao minimum punih proteklih dana između "jednog januarskog dana" i "jednog majskog dana"). Znamo da februar može imati i 29 dana ako je u pitanju prestupna godina. Međutim, ukoliko bi se nameštanje satova odigralo prestupne godine, između "jednog januarskog dana" i 1. maja u ponoć bi proteklo minimum 90 dana i 12 sati, što je više od već izračunatih 90 dana. Dakle, razgovor se vodio proste, a ne prestupne godine.
Gle čuda, upravo jedan kandidat (1980. godina) za godinu nameštanja satova je prestupan (80 mod 4 = 0). Zato on otpada, i ostaje 1979 godina, kada je bio 47-rođendan Jovanu, koji se dakle rodio 1. maja 1932. godine, te je on stariji od Petra koji se rodio maja 1933 godine.
Dakle, Jovan je stariji i zzzz je bio u pravu :))
[ Bojan Basic @ 15.10.2003. 18:42 ] @
Dobro si pretpostavio vrstu satova (pa nisu valda tih godina postojali digitalci)?  Hteo sam da ti se krvi napijem što ne znaš da sabiraš, ali na vreme si ispravio grešku.
Citat: BOOK:
Gle čuda, upravo jedan kandidat (1980. godina) za godinu nameštanja satova je prestupan (80 mod 4 = 0). Zato on otpada, i ostaje 1979 godina, kada je bio 47-rođendan Jovanu, koji se dakle rodio 1. maja 1933. godine, te je on mlađi od Petra koji se rodio maja 1932 godine.
Dakle, Petar je stariji a ovo je bio moj dokaz da zzzz nije u pravu  )
U svakom slučaju, čestitam na korektnom rešenju (iako si imao dve grube omaške, od kojih si jednu ispravio, a drugu očekujem da ispraviš što pre).  [ BOOK @ 15.10.2003. 21:22 ] @
Citat: Bojan Basic:
(pa nisu valda tih godina postojali digitalci)? :)
Itekako jesu. Nameštanje satova se obavlja 1979-e godine, zar ne?
Citat: Bojan Basic:
Hteo sam da ti se krvi napijem što ne znaš da sabiraš,
Nije mi jasno kako si bio tako brz pa si uspeo da pročitaš prvu verziju posta (Verovatno vi moderatori imate pristup svih verzijama postova...). Inače, ne znam ni otkud ti ovlašćenje da citiraš nešto što ne postoji, ili je postojalo jedno 25 sekundi za obične smrtnike! U svakom slucaju, da si uvek tako brz, mogao bi da vidiš da skoro svaki moj post naknadno ispravljam zbog neke računske greške (onaj Zvonar i one silne trojke sto sam naveo: pola je bilo pogresno sabrano u početku :).
Citat: a drugu očekujem da ispraviš što pre). ;)
Treba izbaciti "je" iz rečenice: "Očigledno je između jednog januarskog i jednog majskog dana mora proteći ceo februar, mart i april" :) [ Bojan Basic @ 16.10.2003. 01:04 ] @
Citat: BOOK:
Itekako jesu. Nameštanje satova se obavlja 1979-e godine, zar ne?
Da, ali satovi datiraju još od njihovog rođenja.
Citat: BOOK:
Treba izbaciti "je" iz rečenice: "Očigledno je između jednog januarskog i jednog majskog dana mora proteći ceo februar, mart i april" 
Ne, nisam na to mislio (ne bavim se jurenjem gramatičkih grešaka po forumu). Greška na koju sam mislio nema presudan uticaj na rešenje zadatka, ali ipak bi bilo lepo da je sve korektno. Mala pomoć: nalazi se u ovoj rečenici:
Citat: BOOK:
Međutim, ukoliko bi se nameštanje satova odigralo prestupne godine, između "jednog januarskog dana" i 1. maja u ponoć bi proteklo minimum 90 dana i 12 sati, što je više od već izračunatih 90 dana. Citat: BOOK:
onaj Zvonar i one silne trojke sto sam naveo: pola je bilo pogresno sabrano u početku 
Zašto si tako strog prema sebi, pa samo 2 komada je bilo pogrešno?
Citat: BOOK:
(1,1,2450) = 2452
(1,2,1225) = 1228
(1,5,490) = 496
(1,7,350) = 358
(1,10,245) = 256
(1,14,175) = 290
(1,25,98) = 190
(1,35,70) = 106
(1,49,50) = 100
(2,5,245) = 252
(2,7,175) = 184
(2,25,49) = 76
(2,35,35) = 72
(5,5,98) = 108
(5,7,70) = 82
(5,10,49) = 64
(5,14,35) = 54
(7,7,50) = 64
(7,10,35) = 52
(7,14,25) = 46 
Nemoj se ljutiti zbog ovog, malo se šalimo  Inače, nisam verovao da će neko tako brzo rešiti zadatak.
[ BOOK @ 16.10.2003. 11:21 ] @
Dakle, sad je sve jasno: sve bivše verzije poruka se čuvaju...
Možda ovako:
Citat: BOOK:
Međutim, ukoliko bi se nameštanje satova odigralo prestupne godine, između "jednog januarskog dana u podne" i 1. maja u ponoć bi proteklo minimum 90 dana i 12 sati, što je više od već izračunatih 90 dana. Citat: Zašto si tako strog prema sebi, pa samo 2 komada je bilo pogrešno?
E, to što si citirao ti je samo jedna od poslednjih verzija trojki :))) Izgleda da prethodne nisam ni postovao, već sam radio "Pogledaj kako poruka izgleda". To (nadam) se ne možeš da otkriješ... [ Bojan Basic @ 16.10.2003. 11:45 ] @
Citat: BOOK:
Međutim, ukoliko bi se nameštanje satova odigralo prestupne godine, između "jednog januarskog dana u podne" i 1. maja u ponoć bi proteklo minimum 90 dana i 12 sati, što je više od već izračunatih 90 dana.
Neće biti ni tako... Možda sam pogrešno protumačio rečenicu, ali ako dobro shvatam, ti tvrdiš da će se satovi poklopiti u ponoć... Razmisli malo. [ BOOK @ 16.10.2003. 12:03 ] @
Dobro, možda je sada red i na mene. Evo jedan od mojih omiljenih, istina lakih:
Code:
Zadatak 15:
Neki seljak ima kozu i livadu u obliku kruga poluprečnika 10 metara. Kozu treba da
veže kanapom za kolac zaboden negde na ivici livade tako da koza može da popase
tačno pola livade. Kolika treba da bude dužina kanapa?
Evo i mini-zbirka dosadašnjih "rešenja" i komentara:
1. Ajde, molim te, gde si ti video livadu u obliku kruga?
2. Neka prokopa rov kojim će podeliti livadu na dva jednaka dela i pustiti kozu
3. Neka počupa travu sa pola livade
4. Neka kupi još jednu sličnu kozu koja će da jede istom brzinom kao prva
5. Neka ubije kozu
6. Zašto kolac mora biti baš na ivici livade, a ne u centru?
7. A koji k**** je kupovao livadu o obliku kruga?
8. Neka proda livadu i kupi drugu
Samo je poslednje zaslužilo komentar: time što će kupiti na primer livadu u obliku kvadrata, ne pojednostavljuje mnogo problem... Šta više, to je novi zadatak, koji može da ispadne mnoooogo teži ako se uopšti:
Code:
Zadatak 15':
Neki seljak ima kozu i livadu u obliku kvadrata stranice 10 metara. Koza je vezana
kanapom za kolac zaboden negde na ivici livade. U zavisnosti od mesta gde je
seljak zabo kolac, odrediti potrebnu dužinu kanapa tako da koza popase tačno pola
livade.
[ BOOK @ 16.10.2003. 12:12 ] @
Citat: Bojan Basic:
Možda sam pogrešno protumačio rečenicu.
Jesi, pogrešno si je protumačio, iako mislim da sam je dobro sastavio. Rečenica ustvari kaže: ako bi bila u pitanju prestupna godina, čak i da su namestili satove poslednjeg dana januara u podne, do maja meseca treba nam više od 90 punih dana, tj. treba nam minimum 90 dana i 12 sati do trenutka koji predstavlja prelaz 30.april-1.maj. Naravno, izračunali smo da je potrebno tačno 90 dana za poklapanje, te bi se satovi poklopili već 30. aprila u podne. Već prvog maja u ponoć satovi bi prešišali poklapanje i opet bi različito pokazivali. [ Bojan Basic @ 16.10.2003. 12:32 ] @
Zanimljivi zadaci, pozabaviću se njima. Inače, pokušavao sam da ti kažem da satovi u trenutku poklapanja neće pokazivati 12 sati, nego 6 sati popodne (što naravno nije tačno vreme, ali nigde u zadatku ne piše da treba da bude). Verovatno si to zapazio tokom rešavanja, samo neka stoji zapisano.
[ stalker @ 18.10.2003. 19:42 ] @
Ne znam da li je trebalo matematicki (verovatno nije,cim kazes da je kvadrat mnogo tezi),i izvinjavam se zbog ovakvog nacina,ali ja sam uz malo integraljenja i nekim,samo meni znanim,numerickim metodama dosao do rezultata 11.59m,tacnije 11.58728473m.Resenje me mrzi da pisem,ali ako treba...
[ BOOK @ 23.10.2003. 08:44 ] @
Da, to je približna vrednost konačnog rešenja za zadatak sa krugom. Nemoj da te mrzi da pišeš rešenje :), ne bi trebalo da bude dugo, ja imam jedno koje staje u svega četiri reda u Mathematici + (opciono) jedna lepa slika svega da se vidi šta je gde.
Što se tiče numeričkih metoda, da, one se izgleda moraju koristiti, jer se po mom rešenju dobija jednačina nerešiva nekom "analitičkom" metodom.
[ stalker @ 23.10.2003. 11:22 ] @
Jednacina livade je 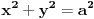 (a je poznato,a je 10)
Jednacina kruga koji opisuje koza je 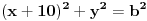 (b trazimo)
Prvo nadjemo tacku x, ona je (oduzmu se dve jednacine) 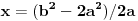
Prema slici 

I konacno resenje,koje se relativno lako dobija (zbog moje,nazalost, operisanosti u tex-u) je na slici.Slika i sve na njoj je napravljena sa GrafEq programom,a i resenje je tako nadjeno.Znaci, napravio sam f-ju
 i trazio presek sa nulom.Zumiranjem dobijenog grafika dobija se preciznost koja nam je potrebna.(sta se zove improvizacija:) [ stalker @ 24.10.2003. 18:40 ] @
Evo resenja nekog i za kvadrat:
Posto trazimo r u funkciji d posmatramo samo  zbog simetrije kvadrata.
Nije bitno za ovo resavanje,ali funkcija kruga je  , a kvadrata 
Sada povrsinice:
 gde je:
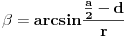
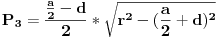
Ista sema dalje:
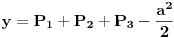
i trazimo presek sa nulom.
E,sad ima i druga fora.Ukoliko krug ne sece kvadrat na pravoj 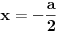 nego po pravoj 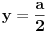 ,  se menja i dobija oblik kao  (prosto je,mrzi me da pisem) i dobija se jos jedna trougaona povrs iznad x ose oblika kao  .Jedini problem je odrediti uslov kada koristiti jednu, a kada drugu jednacinu (normalno, u njoj ne sme da figurise r).To nisam uspeo da provalim, a nisam siguran ni da moze.Najlaksi nacin je da kada fiksiramo d, probamo obe formule jedna ce seci y osu, a druga nece. [ stalker @ 24.10.2003. 20:16 ] @
Jel to neko nepisano pravilo da onaj ko resi zadnji zadatak, postavlja novi.Ukoliko nije, trebalo bi da bude:)(bice zanimljivije)
Ovaj zadatak je preuzet iz Politikinog zabavnika,ne znam koji broj.Nisam kupovao doticni,pa...otkad sam naucio razlomke, ali sad mi je slucajno dosao ruke i odusevio sam se (ponovo).Cak ima tekst o Wiles-u i LFT,besmrtnosti,astronomiji...Ovaj zadatak sam nasao u rubrici Zabavnikove pitalice ili tako nesto.Znaci,ko ima broj, ne odgovara.
Code:
Zadatak 16.
Da bi kandidat za predsednika SAD postao predsednik SAD
mora da budu ispunjeni sledeci uslovi:
1.Kandidat ima preko 35 godina
2.Kandidat ima drzavljanstvo SAD
3.Kandidat nije osudjivan
4.?
Koji jos vazan uslov fali?
[ darkosos @ 24.10.2003. 21:39 ] @
Da je ziv?
[ stalker @ 24.10.2003. 23:44 ] @
mmmmm,nije.Posto ocigledno,sad se vidi,zadatak ima "rupa",da uvedemo konvenciju da je to obuhvaceno 2. uslovom iz zadatka(mrtav covek nema drzavljanstvo).
P.S. Ovakvih sporednih uslova ima kilo sigurno,ali ostaje onaj najbitniji,samo citajte pazljivo;)
[ srki @ 24.10.2003. 23:52 ] @
Da je rodjen u SAD. Kakve veze to ima sa matematikom.
E da, postoji uslov i da nije predsednik jer ne moze da postane ako vec jeste.
[ Shadowed @ 24.10.2003. 23:56 ] @
Da se kandiduje.
[ filmil @ 25.10.2003. 01:04 ] @
Da ga izaberu?
[ stalker @ 25.10.2003. 11:26 ] @
Sve su ovo bili tacni odgovori,however filmil je bio najtacniji od tacnih (komunizam?).Kad se bolje procita,sve je jasno.Znaci, jos jedan uslov je da bude izabran,tj da pobedi na izborima.
[ Bojan Basic @ 25.10.2003. 11:41 ] @
Citat: stalker:
Jel to neko nepisano pravilo da onaj ko resi zadnji zadatak, postavlja novi.Ukoliko nije, trebalo bi da bude:)(bice zanimljivije)
Nije uvedeno to pravilo, i ne želim da ga uvodim iz dva razloga:
1. Ako neko ima lep zadatak, a ne zna da reŠi prethodni, mora da čeka da se pojavi zadatak koji zna da reši, pa tek onda da objavi svoj (ako do tada ne izgubi volju za objavljivanjem);
2. Ako neko zna da reši zadatak, a nema neki koji bi postovao, taj će postovati bilo koji zadatak koji nema veze sa temom. Ja neću brisati ničije zadatke, svako ima svoj ukus, ali ipak bi bilo bolje da niko ne postavlja zadatke "na silu".
[ darkosos @ 25.10.2003. 16:02 ] @
Da, cim sam procitao filmil-ov odgovor znao sam da je to.
Ali zar to sto je neko vec kandidat ne povlaci da ispunjava one uslove?
Dakle, kandidatu je dovoljno samo da bude izabran, a ostalo se podrazumeva; tu je samo da skrece paznju ;-)
Anyway, dobra je dosetka.
[ BOOK @ 30.10.2003. 09:38 ] @
Al' ste se raspričali, a sve na pogrešnom mestu... :)
Evo jedan od najlepših zadataka Vladimira Stojanovića:
Code:
Zadatak 17:
Uzmite bilo koji trougao i uradite trisekcije za sva tri ugla.
Odgovarajuće tri tačke gde se seku "trimetrale" uglova su
temena jednakostraničnog trougla. Dokazati.
[ stalker @ 18.11.2003. 09:17 ] @
A jel moze neka, onako, lepa slika. Cisto za nas debile...
[ noviKorisnik @ 18.11.2003. 09:22 ] @
Baš. Kaj mu dojde "trisekcija" & "trijametrala"?
[ Shadowed @ 18.11.2003. 11:39 ] @
Trisekcija je deljenje na tri jednaka dela (tri_sekcija - tri sekcije (dela)). A trimetrale su (slicko kao simetrale) prave koje dele na ta tri dela.
[ noviKorisnik @ 18.11.2003. 12:46 ] @
ok.
Čisto da proverim da je lekcija naučena:
- imam ugao, povučem dve prave (trijametrale) kroz teme ugla i tako dobijem tri jednaka ugla (trisekcije).
Znači, u igri su 6 trijametrala od ukupno 3 ugla jednog trougla koje se međusobno seku.
Kako se u postavci pominju samo 3 presečne tačke, to prvo treba dokazati da se za proizvoljni trougao poklapaju preseci jedne trijametrale s trijametralama oba ugla (odnosno, jedna trijametrala ima samo 2 presečne tačke). Ovo je možda trivijalno, ali ne i meni zarđalom koji nije znao ni šta je to trijametrala.
[ chupcko @ 18.11.2003. 13:48 ] @
Eh, dodatak je da se sve to lepo nacrta lenjirom i sestarom :)
Samo tacne konstrukcije se priznaju :))).
[ Gojko Vujovic @ 18.11.2003. 14:05 ] @
Ja sam mislio da je nemoguće samo lenjirom i šestarom uraditi trisekciju ugla (bez uglomera dakle). Je l se to nešto promenilo? :)
[ chupcko @ 18.11.2003. 15:09 ] @
Naravno da nije, ali je cinjenica da to ljudi neznaju, pa sam ocekivao da ce neko da se primi i da krene da konstruise :)))).
Po meni je to lep zadatak: za svaki ugao konstruisati treci deo ugla samo lenjirom i sestarom :).
[ BOOK @ 19.11.2003. 17:12 ] @
Nije moguća trisekcija ugla konačnim postupkom uz pomoć lenjira i šestara, ali je to najmanje bitno za ovaj zadatak.
Međutim, na vaše insistiranje :), nacrtao sam odokativno sliku:

Dakle, AD i AE su trimetrale ugla CAB, CD i CF su trimetrale ugla ACB, a BE i BF su trimetrale ugla ABC, za bilo koji trougao ABC. Trimetrala je kao što je već rečeno, jedna od dve prave koja deli ugao na tri jednaka dela.
Treba dakle dokazati da je površina u plavom, tj. trougao DFE jednakostraničan.
[ Ovu poruku je menjao Bojan Basic dana 23.11.2003. u 13:29 GMT] [ Bojan Basic @ 20.11.2003. 02:04 ] @
Trisekcija ugla je moguca sa greskom u najgorem slucaju 0.5% (dovoljno malo da bi bilo zanemarljivo, mada se malim usloznjavanjem postupka moze jos poboljsati, ako je potrebno). Za vikend cu napisati postupak u novoj temi.
[ chupcko @ 20.11.2003. 08:17 ] @
Pa da pojasnim, ovo je tema: najlepsi zadatak, a meni se cini da je sledeci zadatak najlepsi (obrazloicu kasnije zasto):
Za proizvoljni ugao koristeci samo lenjir i sestar (na uobicejene nacine :))) ) konsturisati ugao cija je mera trecina mere datog ugla.
Uobicajeni nacini koriscenja lenjira i sestara su sledeci:
-kroz dve tacke mozemo povuci pravu (lenjirom)
-iz jedne tacke mozemo opisati kruznicu (sestarom) tako da druga tacka pripada kruznici.
-ako se dve prave ili dve kruznice ili prava i kruznica seku mozemo konstrusiati presecnu tacku(e).
E sto ja ovaj zadatak smatram lepim: pa dugo su se ljudi mucili da ga rese (od stare grcke, pa do renesanse), cak i kada je dokazano da nema resenje, gomila ljudi i dalje pokusava da ga resi, ni jedna akademija nauka vise ne prima nikave radove vezane za trisekciju ugla, ali bar jednom godisnje neke novine pisu kako je neko najzad resio :)). Poslednji meni znan slucaj je clanak u magazinu, nedeljnom dodatku politici, gde profesorka matematike (koju slucajno znam) tvrdi da je najzad resila uz pricu: hteli su da sprece sveti srpski duh nauke ..., ali ja sam uspela da konstruisem ;)))).
Eto u tom smislu sam pominjao trisekicju, po meni je to primer lepog, jednostanvog zadatka za koji je dokazano da nema resenja, ali ipak se ljudi mucu :).
[ chupcko @ 20.11.2003. 08:22 ] @
Citat: Bojan Basic:
Trisekcija ugla je moguca sa greskom u najgorem slucaju 0.5% (dovoljno malo da bi bilo zanemarljivo, mada se malim usloznjavanjem postupka moze jos poboljsati, ako je potrebno). Za vikend cu napisati postupak u novoj temi.
:) pa tako ja konsturisem duz cija je mera pi sa greskom manjom od 5% (duz mere 3 :))) ).
A ako konstruisem duz cija je mera 3.14 greska je oko 0.05 % :)
Doduse moram priznati da inzinjerima sasvim odgovara konstrukcija uz odgovarajucu gresku, ali ne i matematicarima :). (stvar ideala, a ne prakticnosti :))) ).
[ stalker @ 20.11.2003. 09:08 ] @
Citat: chupcko:
...gde profesorka matematike (koju slucajno znam) tvrdi da je najzad resila ..., ali ja sam uspela da konstruisem  ))).
A ja imam resenje ovog zadatka, ali mi margina ne es-u nesto mala 
[ Bojan Basic @ 20.11.2003. 10:23 ] @
chupcko, kao sto si i sam rekao, dokazano je da je to nemoguce. Ali, konstrukcija koju cu ja prikazati prakticno daje sasvim zadovoljavajuce rezultate, a greska se moze smanjiti na proizvoljno mali broj.
[ stalker @ 20.11.2003. 11:54 ] @
Koliko se ja secam, svaki ugao koji moze da se izrazi analiticki (preko korenja...) moze da se konstruise. To vazi i za polovine( cetvrtine...) uglova. Cini mi se da aludiras na Tejlorov razvoj, ukoliko je tako, bice zanimljivo!!!
[ chupcko @ 20.11.2003. 15:15 ] @
Pa znam sta si rekao, samo navodim sto ja ovo smatram najlepsim zadatkom :)
Uglavnom postoji puno pomocnih sprava koje omogucavaju dodatne kosntrukcije, jedna sprava je onako bas slatka i moze se iskoristiti za konstrukciju elipse u jednom potezu :))).
Cak sam se jednom zanosio idejom da je realizujem fizicki, ali kako imam tri leve ruke i jednu levu nogu ...
Sacu ja da nabudzim drgeo da prikazuje i trisekcije ugla :), pa cemo da vidimo da li je tacna ona nova (za mene) osobina trougla :).
[ roentgen @ 20.11.2003. 15:53 ] @
Cao!
[ Bojan Basic @ 20.11.2003. 19:40 ] @
Kakav crni Tejlorov red, svaki osnovac moze to da uradi, konstrukcija je zapanjujuce jednostavna. Sad zaista ne mogu da napisem, dobicete u subotu uvece.
[ Bojan Basic @ 23.11.2003. 11:48 ] @
Evo, napisao sam postupak ovde, molim vas da komentare i ostalo pišete tamo, a ne ovde. [ stalker @ 05.12.2003. 10:49 ] @
Resio kolega koji je zeleo da ostane anoniman. Nisam pri vremenu da nesto lepse crtam, nadam se da ce svi razumeti.

Po II Kirhofovom zakonu pisemo jednacine za konture:
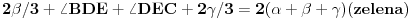

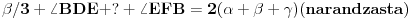
Po I Kirhofovom pisemo oko tacke E:
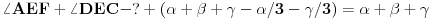
Ovde su nam nepoznati uglovi (pored naseg ?) jos i :BDE,DEC,AEF,EFB. Znaci imamo 4 jednacine sa 5 nepoznatih, ali AEF i DEC mogu zajedno da se pokrate, pa za ? dobijamo
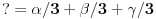 sto je 60 stepeni.Tako se postupak nastavlja za preostala 2 ugla izborom pogodnih cetvorouglova.
[ stalker @ 05.12.2003. 10:54 ] @
Evo ovako, sada je bio svetski dan borbe protiv side, pa u skladu sa tim jedan lep, dosta lagan zadacic:
Code:
Zadatak 18.
Tri mornara i prostitutka
Bilo tri mornara i jedna prostitutka i svaki od njih je hteo da radi "ono"
sa prostitutkom, ali problem je bio sto su imali samo 2 kondoma,
a hteli su da budu sigurni da niko nece da se zarazi.
Sumnja se da jedna od te 4 osobe ima AIDS, ali se ne zna koja.
Mogu li mornari da se zadovolje sa prostitutkom, a da niko sigurno ne dobije bolestinu neku?
Namerno rekoh sa njom, posto je bilo varijanti samo i gay zadovoljavanja. Zadatak je prilicno poznat, pa ko zna nek cuti, da ostane bar jedan dan [ noviKorisnik @ 09.12.2003. 11:52 ] @
Jel' moguće bezbedno zadovoljenje bez upotrebe kondoma? Samozadovoljenje? Ili postoji matematički hint? Možda se zna bar jedna osoba koja nije pozitivna?
[ chupcko @ 09.12.2003. 13:32 ] @
eh, secam se ovog, doduse u varijanti sa hiruskim rukavicama, cak mislim da sam dobio neku nagradu bas na ovom zadatku nekada davno.
Ajde mali hint, svaki kondom ima dve strane koje su ciste (jelte, kada kondom izvrnes, dobijes kondom,
+/- neke kreme :) ).
Dakle dva kodnoma, dve strane sve ukpuno 4 cistih strana, jedna osoba sa 3 ostale zeli sex, pa ajde malo kombinujte.
[ noviKorisnik @ 10.12.2003. 11:29 ] @
Hvala na hintu...
Mornar 1 stavi kondom A.
Mornar 1 stavi kondom B.
Mornar 1 se zadovolji s prostitutkom.
Mornar 1 skine kondom B.
Mornar 1 skine kondom A.
Mornar 2 stavi kondom B.
Mornar 2 se zadovolji s prostitutkom.
Mornar 2 skine kondom B.
Mornar 3 izvrne kondom A.
Mornar 3 stavi kondom A.
Mornar 3 stavi kondom B.
Mornar 3 se zadovolji s prostitutkom.
Mornar 3 skine kondom B.
Mornar 3 skine kondom A.
Mornari baciše kondome na reciklažu, pozvaše prostitutku na čašicu ruma i pitaše je "da li si zadovoljena?"
... čista hirurgija :D
[ stalker @ 10.12.2003. 12:14 ] @
Correct:)
[ Mihailo Kolundzija @ 10.12.2003. 23:01 ] @
Hm, pretpostavljam da je poslednji zadatak inspirisan onim reklamicama što se vrte u vrhu ekrana.
Probaću da potrefim tekst jednog zadatka što beše na Elektrijadi pre par godina (Kopaonik, ako se neko seća). Dakle, moglo bi da bude:
Code:
Zadatak 19:
Imate matricu 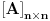 čiji je svaki element 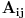 jednak broju zajedničkih delilaca brojeva  i 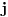 , a treba da odredite vrednost njene determinante.
[ Ovu poruku je menjao Bojan Basic dana 20.12.2003. u 15:26 GMT] [ BOOK @ 11.12.2003. 10:38 ] @
Citat: Mihailo Kolundzija:
Imate matricu  čiji je svaki element 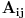 jednak broju zajedničkih delilaca brojeva  i 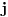 , a treba da odredite vrednost njene determinante.
Za svako n, determinanta matrixa je 1. [ stalker @ 11.12.2003. 11:45 ] @
Ukoliko ja zestoko ne gresim jos u postavci zadatka (sto je vrlo verovatno), determinanta 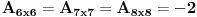 . [ Mihailo Kolundzija @ 11.12.2003. 11:55 ] @
BOOK je dao tačno rešenje, ali je izostavio dokaz.
[ ast. @ 11.12.2003. 14:12 ] @
Citat: Bojan Basic:
Trisekcija ugla je moguca sa greskom u najgorem slucaju 0.5% (dovoljno malo da bi bilo zanemarljivo, mada se malim usloznjavanjem postupka moze jos poboljsati, ako je potrebno). Za vikend cu napisati postupak u novoj temi.
Ma nije problem trisektirati ugao sa ocekivanom greskom, tako mozes da se zadovoljis i odokativnom metodom! Pazi josh je kao shto verovatno znash i cika Gaus dokazao da je to nemoguce i (to vrlo elegantno). Tuzno je sto je ona baka iz Nacija patentirala svoj "izum" kao apsolutni dokaz! Da bi ironija bila veca njen dokaz em shto je pogreshan em shto ona kao da zivi u neolitu! Pa ni stari grci se nisu zadovoljavali samo grafickim dokazom!
Ali dobro ona jadnica prica koliko zna! [ london @ 24.12.2003. 06:25 ] @
Citat: noviKorisnik:
Hvala na hintu...
Mornar 1 stavi kondom A.
Mornar 1 stavi kondom B.
Mornar 1 se zadovolji s prostitutkom.
Mornar 1 skine kondom B.
Mornar 1 skine kondom A.
Mornar 2 stavi kondom B.
Mornar 2 se zadovolji s prostitutkom.
Mornar 2 skine kondom B.
Mornar 3 izvrne kondom A.
Mornar 3 stavi kondom A.
Mornar 3 stavi kondom B.
Mornar 3 se zadovolji s prostitutkom.
Mornar 3 skine kondom B.
Mornar 3 skine kondom A.
Mornari baciše kondome na reciklažu, pozvaše prostitutku na čašicu ruma i pitaše je "da li si zadovoljena?
... čista hirurgija :D
[ Ovu poruku je menjao london dana 24.12.2003. u 17:35 GMT] [ noviKorisnik @ 24.12.2003. 06:55 ] @
Antune, nemoj da zbunjuješ. Stavio si svoj komentar unutar citata, oči mi ispadoše dok nađoh Citat: Lepo resenje ako se zna da ONA ima sidu
ali u pitanju je spomenuto 4 osobe Proveri još jednom, jeste čista hirurgija i sida ostaje tamo gde jeste. [ london @ 24.12.2003. 15:41 ] @
Izvini Dejane na ubacivanju u citat.
Mislio sam da ce se sam odvojiti.
Stisnuo sam odgovor sa citatom i mislio da ce logicki da ih odvoji.
Nov sam ovde kao sto si mozda primetio.
[ noviKorisnik @ 25.12.2003. 14:30 ] @
Citat: london:
Izvini Dejane na ubacivanju u citat.
Mislio sam da ce se sam odvojiti.
Stisnuo sam odgovor sa citatom i mislio da ce logicki da ih odvoji.
Nov sam ovde kao sto si mozda primetio.
... ma to je najmanja frka 
[ blaza @ 27.12.2003. 18:37 ] @
Ovo je resenje Pola Diraka, cuvenog fizicara nobelovca iz 1926. godine.
[ BOOK @ 17.01.2004. 22:56 ] @
Oprosti, ali to je MOJE rešenje, bez obzira što je tamo neki pokojnik sasvim slučajno našao isto rešenje kao i ja...
Bojan Bašić: obrisan nepotreban citat
[Ovu poruku je menjao Bojan Basic dana 18.01.2004. u 01:10 GMT]
[ BOOK @ 17.01.2004. 23:02 ] @
Evo još jedan lepotan:
Code:
Zadatak 20:
Svaki prirodan broj se na mnogo načina može predstaviti kao zbir drugih prirodnih
brojeva. Na primer, broj 5 se može napisati kao 1+1+1+1+1, 1+1+1+2, 1+1+3,
1+2+2, 1+4, 2+3 i najzad samo kao 5.
Naći za svaki prirodan broj (tj. naći opštu formulu) takvo rastavljanje na sabirke da
oni daju najveći mogući proizvod kada se pomnože. Na primer, u gornjem primeru to
je rastavljanje 5=2+3 (2*3=6).
p.s
Glava ću vam se ponaotkidati ako se budete uhvatili programiranja. [ blaza @ 18.01.2004. 05:49 ] @
Citat: BOOK:
Oprosti, ali to je MOJE rešenje, bez obzira što je tamo neki pokojnik sasvim slučajno našao isto rešenje kao i ja...
U redu je... ja sam samo napomenuo da je Pol Dirak prvi resio taj zadatak, a, kako si ti dosao do istog resenja, treba da si ponosan jer razmisljas kao cuveni nobelovac. [ Mihailo Kolundzija @ 18.01.2004. 06:35 ] @
On Sun, 18 Jan 2004 00:02:07 CET, BOOK wrote:
Citat:
Code:
Zadatak 20:
Svaki prirodan broj se na mnogo načina može predstaviti kao zbir drugih
prirodnih
brojeva. Na primer, broj 5 se može napisati kao 1+1+1+1+1, 1+1+1+2, 1+1+3,
1+2+2, 1+4, 2+3 i najzad samo kao 5.
Naći za svaki prirodan broj (tj. naći opštu formulu) takvo rastavljanje na
sabirke da
oni daju najveći mogući proizvod kada se pomnože. Na primer, u gornjem
primeru to
je rastavljanje 5=2+3 (2*3=6).
Da pokušam:
 [ BOOK @ 18.01.2004. 07:53 ] @
Dobro si pokušao. Još kad bi rekao zašto bio bih jako srećan.
[ stalker @ 18.01.2004. 10:11 ] @
Pa, programiranjem:))))
[ Mihailo Kolundzija @ 18.01.2004. 12:43 ] @
On Sun, 18 Jan 2004 08:53:10 CET, BOOK wrote:
Citat:
Dobro si pokušao. Još kad bi rekao zašto bio bih jako srećan.
Šta ću - zadatak mi se učinio interesantnim, pa reko', 'ajd' da pokušam da
ga uradim. Eto zašto.
A ako te zanima dokaz zadatka, pokušaću i njega da dam. Prvo, postavka
zadatka me je odma' asocirala na dinamičko programiranje, al' reko', da ja
ipak sačuvam tikvu, i da se manem te jeresi u startu. Međutim, to mi je
dalo ideju da rastavljanje 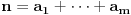 nije
optimalno u slučaju da se bilo koje 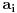 može predstaviti kao
suma prirodnih brojeva čiji je proizvod veći od njega samog (da ne bude
zabune, mislim na 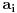 ). Kako se svaki prirodan broj veći ili
jednak četiri može predstaviti na ovaj način, pošto je za njih, recimo,
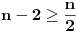 , to nam u igri ostaju samo brojevi 2 i
3, pošto za njih tak'o rastavljanje ne postoji (slučaj kad je n jednako
jedan je trivijalan, i ne uključuje nijedan od ova dva broja). Dalje, kako
je neopravdano imati više od dve dvojke u tom "rastavljanju", jerbo se
2+2+2 mož' zameniti sa 3+3, a da se dobije na proizvodu, to nam ostaje da
gomilamo trojke, a dvojke koristimo samo ako nam "pretekne". I tako, da ne
dužim, dobijem ono što sam napisao, sa dodatkom da se one dve dvojke
javljaju iz razloga što daju veći proizvod od trojke i jedinice (mada je i
jedna četvorka mogla da stoji umesto njih).
E sad, kad sam ja bar pokušao da dam nešto što bi se moglo nazvati
pokušajem dokaza, molio bih te da nas usrećiš sa dokazom onog zadatka sa
determinantom koji si rešio pre izvesnog vremena (pogledaj nekoliko poruka
pre ove), pošto mislim da će to zadatak učiniti mnogo zanimljivijim.
Na kraju za Branka, pošto sam video da se žali da nema neku tablicu
integrala - pogledaj ftp://shell.shore.net/members/w/s/ws/Support/cheat.pdf
[ BOOK @ 18.01.2004. 18:36 ] @
Lepo si to objasnio. Iako nije sasvim formalno, rešenje se ipak vidi i to sasvim jasno. Zadatak je samo lep, nije uopšte težak :(
Što se tiče onog zadatka sa determinantom matrice, nisam mogao da odolim iskušenju jeresi :)
[ Mihailo Kolundzija @ 18.01.2004. 23:32 ] @
Dobro, sad videh da je bilo i nekih sitnih grešaka u onome što sam napisao,
ali to u suštini ne menja stvari. Možda se mogla primeniti i neka indukcija
kako bi se to dovelo u formalno prihvatljivu celinu, ali valjda nije baš
tol'ko loše ni u onakvom obliku.
Ako onaj zadatak sa determinantom više nikom nije zanimljiv za paćenje,
mogu da dostavim jedno elegantno rešenje, zbog kojeg sam ga baš i postavio
(inače, rešenje nije moje, pošto sam ja kao svako neinventivno i bezidejno
biće krenuo da se patim sa indukcijom, te mi je na kraju ponestalo
vremena). Doduše, baš zbog toga što sam očekivao odgovor kakav si dao,
razmišljao sam i da preformulišem zadatak u formu "dokazati da je ...
jednaka 1" , ali sam na kraju odustao.
I da nadovežem predlog da ako posle određenog vremena niko ne reši zadatak,
a onaj ko ga je postavio zna njegovo rešenje (znači, iz igre otpadaju
zlatni potoci i traženja pomoći), taj isti objavi rešenje kako bi možda
neko pokupio neku interesantnu ideju koja će mu možda jednog dana negde
biti od koristi (šta ćete, nikad se ne zna).
[ darkosos @ 28.01.2004. 18:52 ] @
Već na prvi pogled (tek juče sam ga video) zadatak sa matricom mi se mnogo svideo. Elegantan rezultat je još lepši ako je takvo i rešenje. Mihailo je pokazao već više puta svoje kvalitete u tom smislu. 'Ajd i ja da probam :
Ideja je da se matrica svede na trougaonu, gde su svi elementi ispod glavne dijagonale jednaki 0, a na samoj dijagonali su sve jedinice. (Ako već znamo da je determinanta jednaka 1 onda je ovako nešto sigurno moguće, ali naravno, ne mora da znači odmah da je to i najbolji put.)
Posle dosta raznih pokušaja, ispisivanja sve većih matrica, polako mi je sinulo. Postupak bi se mogao ovako opisati najjednostavnije :
svaku vrstu množimo sa -1 i dodajemo je svakoj sledećoj vrsti čiji indeks sadrži indeks ove koju dodajemo; npr. drugu vrstu, pomnoženu sa -1, dodajemo četvrtoj, šestoj, osmoj itd.... naravno ne moramo da teramo ovo sa svim vrstama, već do [n/2].
U čemu je trik? Svaka vrsta sadrži elemente koji pokazuju koliko njen indeks ima delitelja za odgovarajući indeks kolone. Ako smo prethodni postupak uradili za svaku vrstu-delitelja onda će odgovarajući element vrste biti 0 ako je indeks vrste i kolone različit a 1 ako se polapaju, jer se i sam broj računa kao svoj delitelj. Izuzetak su vrste čiji je indeks prost broj. Posle prvog prolaza, sa prvom vrstom (čiji su svi elementi 1), takve imaju 1 samo na mestima gde je indeks kolone sadržalac njihovog indeksa a ostalo su nule. Naravno prva jedinica se pojavljuje na glavnoj dijagonali. U ostatku postupka, ove vrste ostaju netaknute.
P.S. Osećam potrebu da dam konkretan primer, ali sad me nešto mrzucka. Ko prati uputstva, moći će lako da proveri.
//30.01.
Evo, pošto nema nikakvog komentara, primer :

U prvom potezu, prvom vrstom oduzimamo po jedan u svim ostalim. Drugu vrstu oduzimamo od četvrte i šeste, a treću od šeste. [ vandrija @ 02.02.2004. 23:11 ] @
Da li neko ima resenje za zadatak 20 u C-u ili Pascal-u?
[ BOOK @ 03.02.2004. 11:41 ] @
Nažalost, ovo moje je u Javi, ali program lako možeš prebaciti u C:
Code:
import java.io.*;
class E
{
public static void main (String[] args) throws IOException
{
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
int br = Integer.parseInt(bf.readLine());
if (br<3)
{
System.out.println(br);
return;
}
for (int i=1; i < br/3; i++) System.out.print("3 ");
switch (br%3)
{
case 0: System.out.print("3 "); break;
case 1: System.out.print("2 2 "); break;
case 2: System.out.print("3 2 "); break;
}
}
:)))))
Pretpostavljam da hoćeš program koji nalazi sva moguća rastavljanja i onda za svaki proverava proizvod, te štampa ono rastavljanje kod koga je najveći proizvod. Evo i tog programa (zajebano je, ali to je najjednostavnije što mi trenutno pada na pamet).
Code:
import java.io.*;
class Rastavljanje
{
int x = 0;
int niz[][];
Rastavljanje(int[][] a)
{
niz = a;
}
void rec(int y, int m, int n, int od)
{
if (m==1)
{
niz[x][y] = n;
x++;
for (int k=0; k < y; k++) niz[x][k] = niz[x-1][k];
}
else
{
for (int s = od; s <= n/m; s++)
{
niz[x][y] = s;
rec(y+1, m-1, n-s, s);
}
}
}
public static void main (String[] args) throws IOException
{
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
int br = Integer.parseInt(bf.readLine()), maxp = 0, est = 10000;
int all[][][] = new int[br][][];
for (int m = 1; m <= br; m++)
{
all[m-1] = new int[est][m];
Rastavljanje oe = new Rastavljanje(all[m-1]);
oe.rec(0, m, br, 1);
all[m-1][est-1][0] = oe.x;
}
int pok[] = new int[0], size = 0;
System.out.println("Evo ih sva rastavljanja:");
for (int m = 1; m <= br; m++)
{
for (int i=0; i < all[m-1][est-1][0]; i++)
{
int pp = 1;
for (int j=0; j < m; j++)
{
System.out.print(all[m-1][i][j] + " ");
pp *= all[m-1][i][j];
}
System.out.println();
if (maxp < pp)
{
maxp = pp;
pok = all[m-1][i];
size = m;
}
}
}
System.out.println("Najveci proizvod je za:");
for (int i=0; i<size; i++) System.out.print(pok[i] + " ");
System.out.println();
}
}
Napomena: program je spor, jer se broj rastavljanja astronomski povećava (već za broj 50 treba povećati "est"). [ Mihailo Kolundzija @ 04.02.2004. 17:48 ] @
Citat: darkosos:
Evo, pošto nema nikakvog komentara, primer :
Darko, nećeš verovat', al' to je baš način na koji sam ja radio dotični zadatak. Međutim, potrebno je dokazati da se tim postupkom dobija trougaona matrica, što se može uraditi indukcijom, ali je pomalo komplikovano.
Elegantno rešenje kaže da se naša matrica dobija množenjem matrica X i Y, gde element matrice X ( 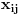 ) ima vrednost jedan ukoliko i deli j, a nula u suprotnom, dok element matrice Y (  ) ima vrednost jedan ukoliko j deli i, a nula u suprontnom.
Kako je determinanta proizvoda dve matrice jednaka proizvodu determinanti tih matrica, to je i determinanta naše matrice jednaka jedan, pošto predstavlja proizvod gornje i donje-trougaone matrice koje na glavnoj dijagonali imaju samo jedinice.
[ darkosos @ 04.02.2004. 22:56 ] @
Elegantno, nema šta!
Doduše nije ni indukcija baš toliki zalogaj. Ako su svi prethodni "sređeni", onda su kod složenih brojeva jedinice samo na glavnoj dijagonali, a kod prostih kako sam već opisao. Ako je naredni broj prost, onda je prosto :), a ako je složen, lako se vidi da iznad iman taman jedinica koliko treba.
U svakom slučaju, rešenje sa dve matrice koje se množe je odlično!
[ nebojsaimarina @ 15.02.2004. 21:10 ] @
Evo i od mene jednog , cini mi se , zanimljivog zadatka.
Code:
Zadatak 21:
Date su 4 homogene kocke A, B , C , D numerisane na sledeci nacin:
A: 1,1,1,5,5,5
B: 2,2,2,2,6,6
C: 3,3,3,3,3,3
D: 0,0,4,4,4,4
Prvo igrac X bira jednu kocku po zelji, a zatim igrac Y bira jednu od preostalih.Onda
svako baca svoju kocku jednom , a pobedjuje onaj koji dobije veci broj.Koji je igrac
u povoljnijem polozaju i zasto?
Zadatak je mozda poznat onima koji su polagali verovatnocu na fakultetu , pa njih molim da se malo strpe sa odgovorima. [ zzzz @ 17.02.2004. 23:58 ] @
samo da još zakomplikujem.
Kad bi četiri igrača odabrala kocke,a onda bacali mnogo puta.U jednom bacanju
bilježi se samo pobjednik.Svaki ima neku šansu da pobijedi.Ako ih na kraju svrstamo
po broju pobjeda,kakav redoslijed očekujete?
A B C D ili nekako drukčije?
[ noviKorisnik @ 18.02.2004. 08:15 ] @
Idem pešački, mrzi me da koristim papir i olovku, a nisam dovoljno razbuđen za napametisanje... i za početak da ponovim uslove
Citat: A: 1,1,1,5,5,5
B: 2,2,2,2,6,6
C: 3,3,3,3,3,3
D: 0,0,4,4,4,4
Prvo igrac X bira jednu kocku po zelji, a zatim igrac Y bira jednu od preostalih.Onda
svako baca svoju kocku jednom , a pobedjuje onaj koji dobije veci broj.Koji je igrac
u povoljnijem polozaju i zasto?
... mada mi je za početak lakše da razmatram Milanovu formulaciju - koji je redosled kockica po broju pobeda kada se pusti dovoljan broj bacanja. To verujem da ima veze s prvim pitanjem.
Mogući ishodi i verovatnoća njihovog pojavljivanja:
a) 1230 (C): 1/2 * 2/3 * 1 * 1/3 = 1/9
b) 1234 (D): 1/2 * 2/3 * 1 * 2/3 = 2/9
c) 1630 (B): 1/2 * 1/3 * 1 * 1/3 = 1/18
d) 1634 (B): 1/2 * 1/3 * 1 * 2/3 = 1/9
a) 5230 (A): 1/2 * 2/3 * 1 * 1/3 = 1/9
b) 5234 (A): 1/2 * 2/3 * 1 * 2/3 = 2/9
c) 5630 (B): 1/2 * 1/3 * 1 * 1/3 = 1/18
d) 5634 (B): 1/2 * 1/3 * 1 * 2/3 = 1/9
Kad sad saberem verovatnoće za kockice skor tabla je:
A: 1/3
B: 1/3
C: 1/9
D: 2/9
... to je sad odgovor na Milanovu formulaciju... Sada da pogledam malo pitanje i analiza (recimo da vidim da li drugi može da nadigra prvog bez obzira na izbor):
- prvi bira A: drugi bira B i u povoljnijem je položaju jer je prvi već hendikepiran u pola bacanja gde dobija jedinicu i sigurno gubi, bez obzira na to šta dobija drugi...
- prvi bira B: drugi bira C i u povoljnijem je položaju jer ga prvi dobija samo ako izvrti šesticu a to je tek svaki treći put...
- prvi bira C: drugi bira D i u povoljnijem je položaju jer tek svaki treći put neće dobiti četvorku koja mu obezbeđuje pobedu...
- prvi bira D: drugi bira A i u povoljnijem je položaju jer gubi samo ako dobije keca (to je svaki drugi put) a prvi ubode četvorku (dva od tri slučaja) što umnoženo dođe da je gubitak svaki treći put...
To je to - nije lako biti prvi [ Piko_u_Prarizu @ 22.02.2004. 18:10 ] @
ovako ja imam jedan zadatak i volio bih znati odgovor, ponavljam ja odgovor ne znam :(
Code:
Zadatak 22:
Nakon dugo vremena srela su se dva prijatelja. Prvi pita drugog: Koliko imas djece?
Tri kcerke.
Koliko imaju godina?
Da mu malo oteza, drugi kaze:
Produkt njihovih godina je 36, a zbroj njihovih godina jednak je broju prozora na
ovoj zgradi kraj koje prolazimo.
Prvi pocne racunati i nakon nekog vremena zastane dvoumeci se oko rezultata, na sto mu
drugi kaze:
Znas, jucer mi je najmladja kcerka pokusala nacrtati kucu olovkom na komadu papira.
Na to mu prvi kaze tocno rjesenje."
Dakle, koliko kcerke imaju godina? Sve je vazno u prici.
hvala, nadam se da netko zna rijesenje, treba neko objasnjenje i nije 1-4-9 a ni 2-3-6
hvala
Bojan Bašić: korigovan prelom poruke
[ Ovu poruku je menjao Bojan Basic dana 22.02.2004. u 21:57 GMT] [ StMilan @ 22.02.2004. 18:33 ] @
Resenje je verovatno 1-6-6.
Prozora ima 13, pa su moguca resenja 1-6-6 i 2-2-9. Zato covek nije mogao odmah da da resenje, a kada mu je prijatelj rekao 'najmladja cerka', zakljucio je da je resenje 1-6-6.
[ stalker @ 22.02.2004. 18:55 ] @
Bilo vec, i to nekoliko puta, ovaj ES se ponavlja (sto je dobro, znaci da imamo sve:)
Ovaj je inspirisano prethodnim zadatkom (sa verovatnocama)
Code:
Zadatak 23:
Par nepar cica maca brundo rundo raz piz dis dizi ruke sad u vis palcevi ne vaaaa-ze
Sta treba izabrati - par ili nepar i koji broj treba podignuti?
Da li je verovatnoca 50%?
Ukoliko nije, kolika je?
Da li ima razlike ako palcevi vaze?
Pretpostavljam da znate na sta mislim:) tako da cu "pravila" igre izostaviti. [ Bojan Basic @ 11.03.2004. 23:35 ] @
Pošto već duže vreme nije dodato novih zadataka, evo jednog od mene:
Code:
Zadatak 24:
Majka je rodila sina sa 21 godinom. Za tačno 6 godina (računajući od danas), majka će
biti 5 puta starija od sina. Gde se trenutno nalazi sinovljev otac? [ noviKorisnik @ 12.03.2004. 00:11 ] @
x je broj godina majke u ovom trenutku.
x + 6 = 5 * (x - 21 + 6) = 5 * (x - 15) = 5x - 75 => 4x = 81 => x = 20.25
... što kaže da će majka roditi sina za 9 meseci. I ja se pitam gde je tata ;)
[ srki @ 12.03.2004. 11:48 ] @
Citat: Majka je rodila sina sa 21 godinom.
Rodila?!?
[ the Lord @ 29.03.2004. 11:47 ] @
Cao svima.
Zanima me da li neko zna resenje za 4. zadatak, onaj sa gospodinom Proizvodom i gospodinom Zbirom, posto izgleda da ga ja nisam bas najbolje razumeo, a nisam naisao na nista o njemu u celom thead-u. Mislim koliko sam ja razumeo zadatak, ako su to brojevi 3 i 4 onda je njihov proizvod 12, a zbir 7. Onda proizvod ne moze da zna koji su to brojevi, je nidu oba prosti, a zbir zna da proizvod ne zna jer on moze biti zbir dva broja koji su oba prosti. Ali takodje to vazi i za 3 i 6, i za 62 i 133 i za ukupno 9718 razlicitih parova brojeva??? Mislim, znam da negde gresim, ali ne znam gde?
[ the Lord @ 29.03.2004. 11:54 ] @
Takodje imam malu nedoumicu u vezi onog zadatka za f(I). Ok je ono da funkcija mora da kada se zarotira za pi/2 da samu sebe, ali onaj primer sa x^2+y^2=R^2, tj krugom nema smisla jer to nije funkcija, vec kriva drugog reda. I trenutno mi ne pada na pamet ni jedna f-ja koja kada se zarotira za pi/2 daje samu sebe. Neki primer bi bio od pomoci, hvala.
P.S. nov sam na forumu i nisam stigao da pogledam kako da koristim tex ili latex, pa izvinite zbog ovakvih izraza.
[ Bojan Basic @ 29.03.2004. 12:56 ] @
Kao prvo, dobrodošao na forum, nadam se da će ti se svideti.
Što se tiče zadatka o dva gospodina, o njemu smo već dva puta nadugačko pričali na http://www.elitesecurity.org/tema/18994 i http://www.elitesecurity.org/tema/28130, pročitaj to sve pa ako ti i dalje nije jasno pitaj u drugoj temi koju sam naveo.
A što se tiče funkcije, nisam tačno sigruran na šta misliš, ali čini mi se da si propustio Brankov odgovor, pogledaj još jednom ovu poruku: http://www.elitesecurity.org/poruka/200146. [ the Lord @ 29.03.2004. 23:06 ] @
Hvala na toploj dobrodoslici i mislim da mi se vec svidja.
Hvala ti za link ka temama sa onim zadatkom.
Onaj Bojanov post sam propustio, verovatno zato sto nije dao nacin na koji je dosao do resenja. Pa bih ga ovom prilikom zamolio da mi objasni posto me jako zanima. Kada sam pisao predhodni post mislio sam na roentgen-in (majin) post (njen nik sam morao da copy paste) i to samo na geometrijsko resenje.
[ Bojan Basic @ 29.03.2004. 23:16 ] @
Dok se Branko ne javi sa objašnjenjem svog toka razmišljanja možda ti ova ideja pomogne: http://www.elitesecurity.org/poruka/198176. [ stalker @ 30.03.2004. 16:35 ] @
Ma Srki je to fenomenalno objasnio (ja sam slab teoreticar:)
Ja sam razbio problem na 4 kvadranta i razmisljao sta gde treba da bude da bi se preslikalo tamo gde treba. Posle je igrarija odabrati ogranicenu i njoj inverznu f-ju. (Mislim da sam ja uzeo arctg - inace meni omiljena funkcija;)
[ the Lord @ 30.03.2004. 20:48 ] @
Jos jednom hvala sto ste bili dobri prema meni i ukazali mi na resenje zadatka.
[ stalker @ 03.04.2004. 15:50 ] @
Posto su meni najlepsi zadaci oni koji imaju neocekivano resenje, a posto se ovih dana zezam sa verovatnocom, evo jednog (lepog):
Code:
Zadatak 25.
U sobi se nalazi n osoba. Koliko najmanje treba da bude n
da bi verovatnoca bila preko 99% da bar dve osobe iz te grupe
slave rodjendan istog dana?
[ zzzz @ 04.04.2004. 23:25 ] @
Ako su svi rođeni iste godine (neprestupne,recimo maturska zabava) onda je
dovoljno da ih ima 57.Ako su razbacani po godištima bez veze,tj sa šansom da neki
budu i u prestupnoj godini,onda 58 komada.
1-P=0.01=1*(364/365)*(363/365)*....je osjetljiv na grešku,pa sam možda mašio
(u brojanju).Ono 58 zahtjeva malo više teksta.Napisaću i to ako je ovo prvo tačno.
Nisam lupio odoka!
[ stalker @ 05.04.2004. 15:52 ] @
Bravo!!!
E, sad ako mi neko kaze da je ovaj rezultat ocekivan...
[ srki @ 05.04.2004. 18:46 ] @
Jeste, sto ne bi bio?
[ stalker @ 05.04.2004. 22:11 ] @
Pa meni nije:) Tj. bar nije bio dok dobro ne razmislis. I sada kada sam umoran mogu da viknem 'Vau'. U stvari, svi mi razmisljamo da je ta verovatnoca namenjena bas tebi, pa svi imaju odgovor 360 i kusur:) Zapravo, tu su kombinacije svako sa svakim, pa i ima logike
[ Nedeljko @ 09.04.2004. 15:09 ] @
Moram priznati da rešenje zadatka sa funkcijom koje je ponudio učesnik koji je pisao o geometrijskom i analitčkom rešenju (sa beskonačnim matricama) nije prihvatljivo, pre svega zato što implicitno zadana funkcija u opštem slušaju nije funkcija, već u nekoj okolini bilo koje tačke koja zadovoljava jednačinu predstavlja funkciju kojom se neka od nepoznatih izražava preko ostalih. Takođe, u rešenju postoji i jedna greška koja nema veze sa postavkom nego sa matričnim računom. Naime, jednakost
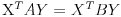
za sve X,Y, gde su A i B kvadratne matrice istog reda, a X i Y kolone odgovarajućeg reda, je ekvivalentna sa 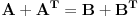 , dok se A=B može zaključiti samo u slučaju da su A i B simetrične matrice. Srkijevo rešenje nije dobro jer ima problem sa time gde se slika nula na osnovu svih onih uslova.
Štaviše, može se pokazati da ne postoji neprekidno rešenje, niti rešenje sa konačno mnogo tačaka prekida, tako da i Chupkovo rešenje otpada. Međutim, njihova ideja je dobra, s tim što je trebalo upotrebiti beskonačno mnogo intervala.
Naime, nulu ćemo preslikati u nulu, a za bilo koji ceo broj  preslikaćemo interval 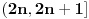 na interval 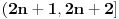 sa 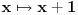 , interval 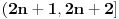 na interval  sa 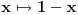 , interval 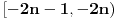 na interval 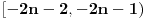 sa 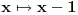 i interval 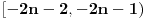 na interval 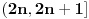 sa 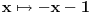 .
Rešenja naravno ima beskonačno mnogo jer za svako rešenje  i realan broj 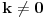 imamo i rešenje 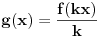 . [ Nedeljko @ 09.04.2004. 16:15 ] @
U vezi zadatka da se dokaže da ne postoji diferencijabilna funkcija koja slika prostor u ravan. E pa ne postoji čak ni takva neprekidna funkcija. Naime, u Topologiji postoji takozvana Borsuk Ulamova lema koja je dokazana metodama Algebarske Toplogije a koja zapravo tvrdi mnogo više. Neka je
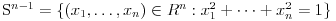
takozvana (n-1)-dimenziona sfera. Tačke  i  na njoj zovemo antipodalnim. Za svaku neprekidnu funkciju 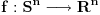 postoje antipodalne tačke koje se slikaju u istu tačku. Budući da je  i da je svaka diferencijabilna funkcija neprekidna, naš zadatak je specijalan slučaj ove teoreme. [ Aleksandar Ilić @ 13.04.2004. 17:52 ] @
Koliko sam primetio niko nije dao odgovor na Zadatak 24 pa reko ja da pokusam.
Majka rodila sina sa 21 godinom. Za tacno 6 godina, ali pise u zagradama racunajuci od danas, majka ce biti 5 puta starija od sina. Posto ovo nema nikakve veze jer za 6 godina majka ce imati 27 godina, a sin 6 godina znaci ne uklapa se.
I sad pitanje glasi gde se nalazi tata?
Pa za tacno 6 godina (racunajuci od danas) sin ce puniti 6 godina i znaci tata ce biti na proslavi njegovog sestog rodjendana.
Jesam li u pravu???
[ Nedeljko @ 13.04.2004. 19:47 ] @
Ne, nisi u pravu! Ako danas majka ima x godina, za 6 godina će imati ona imati x+6 godina, a njen sin x-21+6=x-15 godina, pa pošto mora biti x+6=5*(x-15), dobijamo da majka sada ima 20,25 godina, tj da će sina roditi za 0,75 goduna=9 meseci, što daje nedvosmislen odgovor gde je (sada) otac. To je na ovom forumu već objasnio Dejan Katašić zvani noviKorisnik.
[ Leftist @ 15.04.2004. 23:33 ] @
Niko nije resavao 4. zadatak?
Ja se tripujem da sam ga resio, ali nisam dobio jednoznacno resenje. Mogu li da znam da li je to u redu, cisto da ne ispadnem glup u drustvu : )
P.S. Kad sam provalio da ima vise od jednog resenja napravio sam program koji racuna sva moguca, pa i to mogu da postujem, ako je sva ova prica sa vise resenja dobra...
[ Bojan Basic @ 15.04.2004. 23:38 ] @
Kako niko nije rešio 4. zadatak, imaš o njemu toliko materijala da možeš do sutra da čitaš. Samo skokni do http://www.elitesecurity.org/tema/18994 i http://www.elitesecurity.org/tema/28130. [ chupcko @ 21.04.2004. 08:18 ] @
Malo sam surfao i setio se da je ovde bila rasprava oko onog proizvod suma i ...
Evo nadjoh lepo objasnjeno resenje: pa koga ne mrzi da cita..., takodje ima tu puno lepih zadataka.
http://www.qbyte.org/puzzles/p003s.html
[ devojcica @ 28.04.2004. 17:18 ] @
Cao, kako vam se svidja ovaj
Code:
Zadatak 26:
Dati su brojevi 1, 3, 4, 6. Treba da se dobije 24 koristeci samo operacije +, -, *, / i
svaki od datih brojeva tacno jedanput. [ srki @ 29.04.2004. 00:26 ] @
Znaci ne smeju da se koriste zagrade? I ne sme na pocetku da bude "-" posto se "-" koristi samo kao operacija?
[ noviKorisnik @ 29.04.2004. 01:32 ] @
Teško... Ima 4 operanda i 4 operacije!
Za 4 operanda dovoljne su 3 operacije. 4 operacije zadovoljava 5 operanda.
Ali, u tekstu nije napomenuto da moraju da se koriste sve 4 operacije (samo se kaže da se koriste svi operandi) - tako da mogu da se koriste i samo 3 operacije.
[ devojcica @ 29.04.2004. 16:10 ] @
Smeju da se koriste zagrade, i operacije gde god i koliko god puta je potrebno (ukljucujuci 0 puta i - kao unarnu operaciju, tj. na pocetku).
[ zzzz @ 29.04.2004. 23:50 ] @
Ovo je jako teško riješiti.Ja sam nešto napravio,ali..
da li je dobro?Saćekaću.
[ blaza @ 29.04.2004. 23:55 ] @
6*4-3-1=24
naravno, u oktalnom brojnom sistemu.
[ stalker @ 30.04.2004. 00:35 ] @
(14-6)*3
naravno u decimalnom...
[ blaza @ 30.04.2004. 01:41 ] @
Dati su brojevi 1, 3, 4, 6, a ne cifre 1, 3, 4, 6.
[ srki @ 30.04.2004. 02:53 ] @
posto 6 moze da se okrene naopako da ispadne 9 onda bi resenje moglo da bude:
(1+4)*3+9
[ Bojan Basic @ 30.04.2004. 03:16 ] @
Ili 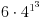 . [ Nedeljko @ 30.04.2004. 13:32 ] @
Nadam se da na ovo rešenje niko neće imati primedbi.
6 / (1 - (3 / 4)) = 24.
[ devojcica @ 30.04.2004. 14:09 ] @
Da to je bilo planirano resenje, ali mi se mnogo svidja ovo oktalno. Za Bojana, nije bilo dozvoljeno stepenovanje.
[ blaza @ 30.04.2004. 16:13 ] @
Postoji i heksadekadno resenje:
1*4*(3+6) = 24
[ zzzz @ 01.05.2004. 00:08 ] @
Postoji i 3155-dnom brojnom poz. sistemu rješenje:
Tj 24 u ovom sistemu je 3155*2+4=6314(dek.)
Ali ipak hajmo reći da je Nedeljkovo rješenje najbolje.
[ Nedeljko @ 01.05.2004. 00:56 ] @
Ako je već do sprdnje, hajde da i ja dam svoj doprinos. U dekadnom brojnom sistemu uz operaciju konkatenacije (nadovezivanja) nizova cifara, koju je zzzz upravo upotrebio, imamo i rešenje
(6-4)(1+3)
budući da je 6-4=2 i 1+3=4.
[ noviKorisnik @ 01.05.2004. 01:15 ] @
Varijacija:
- 6 / ((3 / 4) - 1)
[ flamenco @ 16.05.2004. 00:17 ] @
Da li se zadatak sa bazenom resava jednacinom
(Vo-ma*sqrt(2gz)dt=A(z)dz
[ Nedeljko @ 27.05.2004. 19:52 ] @
Ne. To je zapravo zdatak iz Fizike.
[ malada @ 02.07.2004. 11:46 ] @
Evo jednog zadatka koji je meni bio jako interesantan a nije mnogo tezak.
Code:
Zadatak 27:
Treba napraviti preslikavanje (bijektivno) iz skupa prirodnih brojeva u skup cijelih brojeva
(ili obrnuto).
A sto se tice sedmog zadatka evo rijesenja (ako neko vec nije dao):
Numerisimo gomile od 1 do 10 (odredjenosti radi). Sa prve gomile uzimamo jedan zlatnik, sa druge 2,...,sa 10-te 10 zlatnika stavljamo ih na vagu i iz ocitavanja vidimo na kojoj gomili su zlatnici od 9g, ako su na n-toj tezina ce biti (10+9+8+...+1)*10 - n.
Sto se tice ovog zadatka ja sam ga nasao u jednoj zbirci za matematicku olimpijadu (ako se ne varam) i on se moze uopstiti na n gomila sa uslovom da u n-toj gomili bude najmanje n zlatnika. [ malada @ 06.07.2004. 17:06 ] @
Evom jos jednog interesantnog zadatka:
Code:
Zadatak 28:
U staroj grckoj se sudilo tako sto izdajes pred sudiju i on ti da dva papirica od kojih na
jednom pise kriv a na drugom nevin.
Tako je neki matematicar (recimo) trebao da izadje na sud ali je saznao da se sudija
spremio da ga osudi tako sto ce da mu ponudi dva papirica na kojima (na oba) pise kriv.
Pitanje je kako on da iskoristi to saznanje da se sigurno oslobodi krivice? [ srki @ 06.07.2004. 19:29 ] @
Uzme jedan papiric i pojede ga pa ce ovi morati da procitaju drugi.
[ Gojko Vujovic @ 06.07.2004. 19:38 ] @
srki i na drugom piše KRIV. Ne bi se oslobodio krivice tako da to nije rešenje.
[ Ve$eli @ 06.07.2004. 20:44 ] @
Upravo zbog toga bi se oslobodio. Ako je ostao onaj na kome pise KRIV, znaci da je izvukao i pojeo onaj na kome treba da pise da je NEVIN.
Bojan Bašić: obrisan nepotreban citat
[Ovu poruku je menjao Bojan Basic dana 06.07.2004. u 23:18 GMT]
[ srki @ 06.07.2004. 21:10 ] @
Pa da, to je poenta. Zato sam i napisao da pojede pairic da bi morali da procitaju onaj koji nije izvukao.
[ malada @ 07.07.2004. 16:23 ] @
Evo jos jednog:
Code:
Zadatak 29:
Sam si u sobi sa dvoje vrata i dva brata. Iza jednih vrata se nalaze velike pare a iza
drugih nista. Znajuci da jedan od dvojice brace UVIJEK govori istinu, a drugi UVIJEK
laze (ti neznas koji laze a koji ne) i da obojica znaju gdje se nalaze pare, treba, jednom od njih dvojice, postaviti samo
jedno pitanje da bi sigurno saznao iza kojih vrata su pare. [ srki @ 08.07.2004. 00:37 ] @
Pa najlakse ti je da otvoris bilo koja vrata i ako pare nisu tu onda otvoris sledeca vrata :)
A ako bas hoces da saznas pre otvaranja vrata onda jednom od brace kazes:
"reci mi sta bi tvoj brat rekao iza kojih vrata su pare."
Kada ti kaze odgovor onda znas da tu nisu pare.
[ malada @ 14.07.2004. 12:56 ] @
Posto vidim da znas sve zadatke evo ti jos jedan (koji takodje znas ali nema veze):
Code:
Zadatak 30:
Ljudozderi uhvatili nekog lika i nisu znali dali da ga ispeku ili skuvaju.
I kazu mu:"Reci jednu recenicu, ako bude tacna skuvacemo te a ako bude netacna
ispecicemo te". Dali moze da se oslobodi? [ srki @ 14.07.2004. 18:10 ] @
Ne moze nikako da se oslobodi. Oni nisu rekli da ga nece ispeci ako ga skuvaju i obrnuto pa uvek mogu da ga skuvaju pa da ga posle ispeku :-)
Mada verovatno zelis da ti neko odgovori da treba da kaze: "Ispeci ce te me!"
[ Nedeljko @ 14.07.2004. 19:47 ] @
U tom sličaju, ne mogu da ga ispeku jer bi njegova izjava samim tim postala tačna. Pošto je isključena mogućnost da ga ispeku, mogu eventualno da ga skuvaju bez pečenja. No, tada njegova izjava ne bi bila tačna. Znači jedina mogućnost je da ga ne skuvaju i ne ispeku. No, tada će njegova izjava postati netačna, pa bi trebalo da ga ispeku. Dakle, šta god da mu urade ili ne urade nikako se ne slaže.
[ Tisma @ 14.07.2004. 21:57 ] @
@malada
Ovakav sličan problemčić sam ja postovao:
http://www.elitesecurity.org/tema/47304/0#307951[ malada @ 16.07.2004. 09:56 ] @
E pazite ovo razmisljanje:
Code:
Zadatak 31:
Poznata prica o trci zeca i kornjace (ili neka druga verzija).
Uglavnom trkaju se zec i kornjaca, zec je 10 puta brzi od kornjace a na pocetku
trke kornjaca ima 100 metara prednosti.
Dok zec pretrci tih 100m kornjaca ce za to vrijeme pretrcati 10m, dok zec pretrci
tih 10m kornjaca ce pretrcati 1m, dok zec pretrci 1m kornjaca ce pretrcati 0,1m....
Zec nece nikada stici kornjacu!
U cemu je ovo razmisljanje pogresno? [ srki @ 16.07.2004. 14:37 ] @
Da li ce stici kornjacu ili nece zavisi od toga kako se menja brzina kornjace.
[ malada @ 17.07.2004. 21:29 ] @
Brzine kornjace i zeca se nemijenjaju i zec je 10 puta brzi od kornjace.
[ stalker @ 18.07.2004. 22:19 ] @
Cela tema o pogresnom razmisljanju je ovde.
http://www.elitesecurity.org/tema/6505
Pretrazi malo es pre nego sto postavis zadatak jer su ti svi vec bili
[ 4txx @ 23.09.2004. 20:20 ] @
Cinjenica je da kornjacu zec stize u 11.11(11) sekundi tj na 111.11(11) metru...
A taj trip da ako "zec predje 10m kornjaca 0.1m"..., mozes da koristis samo do te tacke! Izgleda da je nece nikako stici zbog beskonacnosti, ali cim bude 11,11.....2 zec se preci na prvo.
[ dedda @ 22.11.2004. 08:20 ] @
evo jos jedan zadatak:
Code:
Zadatak 32:
Tri radnika obavljaju neki posao. Prvi i drugi radnik ga izvrse za 3 dana, drugi
i treci za 5 dana, a prvi i treci za 4 dana. Za koliko dana bi svaki radnik sam obavio
isti posao.
[Ovu poruku je menjao Bojan Basic dana 04.01.2005. u 16:11 GMT+1][ noviKorisnik @ 22.11.2004. 09:01 ] @
prvi za 120 / 23 dana
drugi za 120 / 17 dana
treći za 120 / 7 dana
[ noviKorisnik @ 23.11.2004. 20:16 ] @
dedda me zamolio da pojasnim ako imam slobodnog vremena... sada imam:
posao = 3 dana (prvi + drugi)
posao = 5 dana (drugi + treci)
posao = 4 dana (prvi + treci)
sistem 3 jednacine i 3 nepoznate
a> 20 posao = 60 dana (prvi + drugi)
b> 12 posao = 60 dana (drugi + treci)
c> 15 posao = 60 dana (prvi + treci)
a - b + c> 23 posao = 120 dana prvi => posao = 120 / 23 dana prvi
a + b - c> 17 posao = 120 dana drugi => posao = 120 / 17 dana drugi
-a + b + c> 7 posao = 120 dana treci => posao = 120 / 7 dana treci
Za koliko dana bi završili posao svi zajedno?
[ kakogod @ 03.01.2005. 22:05 ] @
Code:
Zadatak 33:
upotrebi sve brojeve samo jedanput i koristi samo mnozenje deljenje sabiranje i
oduzimanje da dbijes 24 uz pomoc brojeva 3 , 3 ,8 , 8 tkodje su dozvoljene zagrade. [ bleedoh @ 24.02.2005. 15:26 ] @
majke ti... kako moze sad da se sazna kako se zvao slavkov sin? juuu...
jos to da saznam i sve sve.... lol
[ Zorzo @ 24.03.2005. 15:06 ] @
Već postoji sličan zadatak sa brojevima 1,3,4,6.
Rešenje je 6:(1-(3/4))=24
A rešenje ovog
8:(3-(8/3))=24
[ KPYU @ 18.04.2005. 12:44 ] @
Moj omiljeni zadatak uopšte nije težak, ali ima mnogo zanimljivu formulaciju. To je u
stvari srednjoškolski sistem linearnih jednačina, upakovan u priču. Dakle unzip-ujte ga
& rešite.
Autor zadatka je Sem Lojd. Čuven je po mozgalicama koje su kombinatornog karaktera
te, meni lično, dosadne. Ovaj zadatak ponekad izbacim gimnazijalcima koji se žale da su
im teški zadaci iz sistema lin j-na.
Code:
zadatak 34
AnaMarija
Ana i Marija imaju zajedno 44 godine.
Marija je dva puta toliko stara koliko je Ana bila kada je Marija bila upola toliko stara
koliko će Ana biti kada Ana bude tri puta toliko stara koliko je Marija bila kada je Marija
bila tri puta toliko stara koliko je tada bila Ana.
Koliko godina ima Ana, a koliko Marija?
[ mickeybaki @ 21.04.2005. 21:44 ] @
Ja imam jedno pitanje koje me muci vec 2 nedelje. Potice iz knjige "Matematicar cita novine" Paulos, J. A, a zove se potato paradox:
Code:
Zadatak 35:
You buy 100 pounds of potatoes and are told that they are 99% water. After leaving
them outside, you discover that they are now 98% water. The weight of the dehydrated
potatoes is then a surprising 50 pounds!
Nisam zeleo da prevodim jer se bojim da ima neka jezicka zackoljica... Pomozite...
[Ovu poruku je menjao Bojan Basic dana 29.05.2005. u 13:43 GMT+1][ KPYU @ 21.04.2005. 23:48 ] @
Ne, ovaj, nije. Text je baš tačan.
Naime, u početku imamo 1% suve materije. To je 1 funta (lb).
Kad ispari malo vode, suva materija (ona 1 lb) čini 2% težine krompira, a to znači da ukupno imamo 50 puta veću masu u malo sasušenom krompiru, no u suvoj materiji tj 50 lbs krompira.
[ MOCEVIC @ 12.05.2005. 21:31 ] @
Ako su ta dva brata rođena istog dana, istog mjeseca, to znaci da ako je jedan rođen u petak, i drugi je u petak ali ne taj petak, nego drugi petak ali u istom mjesecu.Eto kako ta dva brata nisu blizanci
[ KPYU @ 17.05.2005. 15:57 ] @
Moćeviću, 'leba ti, gde si čuo da se žena porodi 2 puta u toku meseca. Nedavno se desilo da je žena nosila blizance, te su lekari uspeli da odlože porođaj drugog deteta na par dana, ali ne na nedelju dana. Uz to deca su i dalje blizanci.
Tačan odgovor je da nisu blizanci nego trojke ili četvorke ili petice ili ...
Uzgred budi rečeno, tačan odgovor je već bio dat mnoooogo davno.
[ Bojan Basic @ 29.05.2005. 12:45 ] @
Evo da malo oživim temu pošto duže vremena nije bilo ništa slično:
Code:
Zadatak 36:
Medved pada u rupu dubine 10m i posle 1s udara u njeno dno. Koje je boje medved? [ DjoleStanic @ 29.05.2005. 22:24 ] @
@Bojan Basic
Moze li neki hint?
[ Bojan Basic @ 30.05.2005. 11:03 ] @
Nije ništa spektakularno, samo se treba setiti formule iz fizike koja se koristi u opisanoj situaciji i na osnovu toga izvući neki zaključak, a dalje sve ide lagano :)
[ stf @ 30.05.2005. 17:04 ] @
Ocigledno je da ovde treba da se iskoristi obrazac za slobodan pad: h=gt2/2. Zamenom se dobija da je g=20m/s2, ali to ne daje nikakvo resenje. Znam da postoji razlika za g na ekvatoru i polovima, ali te vrednosti iznose izmedju 9,5 i 10. Cini mi se da se koristeci mozda neki slican, malo komplikovaniji obrazac moze doci do resenja. However, mislim da je medved bele boje, a da je ta rupa na Zemljinom polu.
[ Bojan Basic @ 30.05.2005. 17:47 ] @
Dobro si krenuo da razmišljaš, ali kraj nije dobar (kao što i sam kažeš, g se kreće između 9.5 i 10, tako da čak ni na Severnom polu ne može biti 20). Ni odgovor nije tačan, ali ne posustajte!
[ Bhamby @ 31.05.2005. 02:13 ] @
Code:
zadatak 37:
-1 5 -2 1 2 0,5 ?
12. zadatak na http://www.iqtest.sk/index.php...5fe8efdb67c7094550b91ce29663f7
p.s. čitao sam http://www.elitesecurity.org/tema/48964/1 ali me interesuje i dalje šta je tvorac ovog zadatka mislio [ stf @ 01.06.2005. 12:56 ] @
Evo jednog mog lakog zadatka:
Code:
Zadatak 38:
Kako da uz pomoc brojeva 0,...,9 dobijes 6. Dakle, 10 puta treba dobiti broj 6, a svaki
put po jedan od ovih brojeva se koriste tacno 3 puta.
Vezano za ovaj zadatak sa medvedom, stvarno ne znam gde je na ovoj planeti g=20. Mozda treba da se ubaci pocetna brzina. U zadatku nije naglaseno da li medved ima ili nema pocetnu brzinu, tj. nije receno ''slobodno pada'', vec ''pada''. Ako uzmemo proizvoljnu vrednost pocetne brzine, onda bilo koji medved moze pasti za 1s u rupu dubine 10m. Ako ovo nije tacno, molim te, Bojane, ostavi jos koju ideju. Ako sam prvi obrazac (u proslom javljanju) dobro postavio i ako sam dobro izracunao g, sta uraditi sa g=20. Poz!
[Ovu poruku je menjao Bojan Basic dana 02.06.2005. u 22:33 GMT+1][ Bhamby @ 01.06.2005. 15:34 ] @
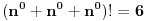
n = 0,1,..,9
Koje operacije su dozvoljene. Nije ovako? [ stf @ 01.06.2005. 18:41 ] @
Ne može da se koristi nulti stepen (onda koristis nulu, ocigledno).
[ Bhamby @ 01.06.2005. 18:58 ] @
Znam da nije, nego dao si 0 u postavci zadatka.
Citat: Kako da uz pomoc brojeva 0,.
Ovo je bitno?
Citat: a svaki put po jedan od ovih brojeva se koriste tacno 3 puta
Važi li ovo:
(1+1+1)! = 6
2+2+2 = 6
[ stf @ 02.06.2005. 08:28 ] @
Da, dobro si izracunao za brojeve 1 i 2. Nulu mozes samo koristiti ukoliko broj 6 dobijas samo sa tri nule, ne i za ostale brojeve.
[ Bhamby @ 02.06.2005. 20:13 ] @
3-3+3! = 6
(4-4:4)! = 6
5+5:5 = 6
6+6-6 = 6
7-6:6 = 6
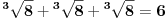 (ovo nije dobro ?)
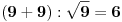 (a ovo?)
[ stf @ 02.06.2005. 20:25 ] @
Po nekom pravilu to sa kubnim korenom ne bi trebalo da bude u redu, ali ni ja drugačiji način nisam uspeo da pronađem. Ostalo je sve u redu. Ostalo je još dobiti broj 6 sa tri nule!
[ Bojan Basic @ 02.06.2005. 20:49 ] @
Citat: stf:
Vezano za ovaj zadatak sa medvedom, stvarno ne znam gde je na ovoj planeti g=20. Mozda treba da se ubaci pocetna brzina. U zadatku nije naglaseno da li medved ima ili nema pocetnu brzinu, tj. nije receno ''slobodno pada'', vec ''pada''. Ako uzmemo proizvoljnu vrednost pocetne brzine, onda bilo koji medved moze pasti za 1s u rupu dubine 10m. Ako ovo nije tacno, molim te, Bojane, ostavi jos koju ideju.
Da, trik jeste u početnoj brzini, ali je bitno kako je medved stekao tu početnu brzinu - nije valjda lansiran iz katapulta :) Odgovor na ovo pitanje otkriće nam dosta toga o prirodi medveda, a samim tim i njegovu boju.
Citat: Bhamby:
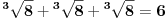 (ovo nije dobro ?)
Ovo definitivno nije dobro jer si očigledno koristio cifru  (i to tri puta). No, evo tačnog rešenja:
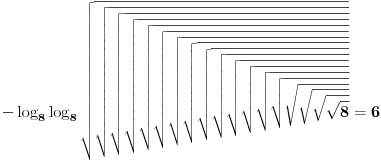
Stvarno divan izraz :) [ Bhamby @ 02.06.2005. 21:32 ] @
A podrazumljiva cifra 2 - 18 x.
[ Bojan Basic @ 02.06.2005. 21:38 ] @
Da, ali to ipak nije isto - ti si napisao cifru  , a ja nigde nisam napisao cifru različitu od  , iskoristio sam činjenicu da je po konvenciji 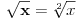 što mi omogućava da ne upotrebim cifru  (a ako sam dobro razumeo zadatak to i jeste poenta).
Da, evo jednostavnog rešenja sa nulama, nije mi jasno da se niko do sada nije setio toga:
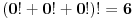 [ Bhamby @ 02.06.2005. 21:56 ] @
U redu je. Samo sam hteo obrazloženje - korektno je.
Za nule. Ipak sam ja odavnooooo bio u školi.
[ Jack the Ripper @ 04.06.2005. 19:11 ] @
Evo nekog zečećeg zadatka:
Code:
Zadatak 39:
Prvog meseca živi jedan par zečeva, svaki par svakog meseca, počev od drugog meseca
svog života donosi na svet još jedan par zečeva. Koliko zečeva ima u 9 mesecu, kolko u
četrnaestom, a kolko u n-tom (izvesti formulu za izračunavanje zečeva) [ Milanius @ 05.06.2005. 11:27 ] @
Sto se tice 39.-og zadatka, reci cu samo sledece:
Leonardo iz Pize (1175-1225), poznatiji po nadimku Fibonaci (tj. Bonacijev sin), je 1202. god. postavio ovaj zadatak.
Stvar se sada cini mnogo jasnijom!
[ Jack the Ripper @ 05.06.2005. 12:06 ] @
Po meni nije problem da vidim kolko ima zecova, ali ne umem da izvedem formulu!
[ uranium @ 05.06.2005. 23:08 ] @
Dakle, ako sa 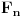 obeležimo broj parova zečeva na početku
 -tog meseca, onda će broj parova na početku 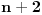 -og meseca biti:
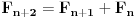
jer, budući da zečevi ne umiru (!?) u 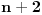 -gi mesec "prelaze" svi oni
parovi koji su postojali i  -og meseca, plus još 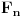
novorođenih parova ( svaki par koji je postojao  -tog meseca, biće polno zreo, ako ne pre, a ono bar 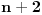 -og meseca i "okotiće" po jedan novi par)
Jack the Ripper-u,
da ne bih sad ovde pisao opšte poznate stvari,
možda je najbolje da pogledaš ovaj link:
http://mathworld.wolfram.com/FibonacciNumber.html
[ Emil Ranc @ 06.06.2005. 00:16 ] @
Još jedan ne tako težak zadačić:
Code:
Zadatak 40:
Imamo pet brojeva - četiri sedmice i jednu jedinicu. Dakle: 7, 7, 7, 7, 1.
Koristeći ovih pet brojeva treba dobiti broj 100. Dozvoljene su osnovne matematičke
operacije (+-*/). Zadatak je postavljen u dekadnom sistemu. [ Jack the Ripper @ 06.06.2005. 08:11 ] @
U svakom slucaju hvala vam !
[ uranium @ 06.06.2005. 09:54 ] @
Evo jednog rešenja za Zadatak 40:
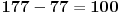 [ stf @ 06.06.2005. 10:15 ] @
Zadatak 40: 100=(7+1/7)*(7+7).
Uranium, u zadatku je naglašeno da su to brojevi, a ne cifre.
[ uranium @ 06.06.2005. 11:11 ] @
Budući da je:  i da je Emilio Ranchez rekao da:
Citat: Emilio Ranchez: Još jedan ne tako težak zadačić:
Code:
Zadatak 40:
Imamo pet brojeva...
nije bilo načina da zaključim da to nisu cifre.
[ manman @ 07.06.2005. 19:22 ] @
Cifra je simbol, znak, kojim sed predstavljaju brojevi.
Kao npr. sto je slovo simbol.
A BROJEVE si ti vec dobio u postavci zadatka, tako da ti ne trebaju novi brojevi.
I na BROJEVIMA se primenjuju operacije +,-,*,/ ( u ovom slucaju jer radi se o brojnom sistemu, dekadnom kao sto je receno, znaci i ovde se opet vidi o cemu je rec)
BROJEVI, BROJEVI..........
[ uranium @ 07.06.2005. 20:35 ] @
Citat: manman: Cifra je simbol, znak, kojim se predstavljaju brojevi.
Kao npr. sto je slovo simbol.
Slažem se. Trebalo je da napišem  .
Ostatak tvoje argumentacije je diskutabilan!
Ali, da završimo već jednom sa tim:
evo jednog "napada" na moje "rešenje":
Citat: Emilio Ranchez: Još jedan ne tako težak zadačić:
Code:
Zadatak 40:
Dozvoljene su osnovne matematičke
operacije (+-*/).
a ja sam upotrebio konkatenaciju (dopisivanje).
Jel možemo sad dalje? 
[ Nedeljko @ 16.06.2005. 16:21 ] @
Istina uranium, rešenje ti nije dobro. Skup cifara ne mora biti podskup skupa celih brojeva. Cifre mogu biti i A,B,C,D,E,F (kao u heksadekadnom sistemu). Ako govorimo o dekadnom sistemu, to znači da cifara ima ukupno deset, i ništa više od toga. Mi brojeve možemo označavati na ko zna kakve sve načine. Cifra (u dekadnom sistemu) je neka od tih deset cifara (obično se obeležavaju sa 0,1,2,3,4,5,6,7,8,9 - to su samo simboli), a jednocifren ceo nenegativan broj (ako govorimo o dekadnom sistemu) je ceo broj (a ne cifra) koji nije manji od nule i nije veći od devet. Dekadnost sistema je bila naglašena da bi se znalo da 100 znači sto, a ne nešto drugo. Koristio si nedozvoljenu operaciju nad datim brojevima.
[ uranium @ 16.06.2005. 22:25 ] @
Pa ja sam se sa svim tim već složio (u prethodnom postu) 
Izgleda da su ovde svi platonisti?
Dakle svi se slažu da je cifra (da ne kažem: šifra) deo sintakse (dakle u opštem slučaju cifra je neka reč -niz nekih primitivnih znakova) a da je broj deo semantike.
E pa, da li je to baš tako?
Koliko mi je poznato, sve definicije prirodnih brojeva (do danas) su sintaksne.
Npr. Peanova definicija podrazumeva da je 0 neki grafički simbol, funkcija sukcesora se interpretira kao dopisivanje jednog stalnog grafičkog simbola npr. neke "recke" : |, tako npr. broj (koga uobičajeno označavamo sa) 7 bi bio zapisan kao 0|||||||.
Ako pogledamo sada fon Nojmanovu definiciju vidimo da ona nije ništa "bolja":
0 je sada neki "ur element" (kome se pokušava "prišiti" semantička senka u vidu praznog skupa) i samo je sintaksa
postala složenija:
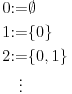
Skrećem pažnju na to da je npr.  samo oznaka za prazan skup. Dakle, sve se i dalje dešava na polju sintakse ma koliko se mi trudili da iz sintakse "uhvatimo" semantiku (ovo liči na onu Ešerovu grafiku sa rukom koja crta samu sebe...)
Moja poenta je: semantiku (koja postoji samo u našim mozgovima) možemo preneti drugima samo kroz sintaksu,npr. ne možeš naučiti dete šta je to broj (koga uobičajeno označavamo sa) 7 a da pri tom ne koristiš neki vid sintakse.
I ono ispravno rešenje koje je dao stf je zapisano pomoću cifara (tj. šifara)...svidelo se to nekom ili ne!
Dakle, formalno govoreći: u matematici postoji samo sintaksa, a Bogu hvala što ne moramo da mislimo samo pomoću nje.
Pa ipak, postoje matematičari (kukala im majka) koji misle da u matematici postoje samo oni objekti koji se mogu efektivno konstruisati.
Najzad, zadaci slični Zadatku 40, vrlo često se zadaju u formi koja implicitno dopušta konkatenaciju.
Da to nije tako, verovatno bi se zadavali u obliku:
Pronaći f-ju
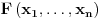
koja je kompozicija f-ja: 
takvu da za zadate brojeve  i  važi 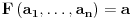 i u čijem se zapisu promeljive  javljaju tačno  puta.
Ovoliko formalističkog čistunstva vodi u paranoju!
[ Nedeljko @ 16.06.2005. 23:44 ] @
Peanovim aksiomama je struktura prirodnih brojeva definisana do na izomorfizam. To upravo znači da nije određeno šta su prirodni brojevi, već samo kako izgleda odgovarajuća struktura. Skup nosač tu može biti bilo koji prebrojiv skup. Cifre dekadnog sistema su pak elementi nekog linearnog uređenja sa deset elemenata. Taj sku (označimo ga sa D) ne mora imati nikakve veze sa skupom prirodnih brojeva N (koji kao što rekoh može biti bilo koji prebrojiv skup). Zapisi prirodnih brojeva su neka preslikavanja skupa  u skup D koja imaju osobinu da sve elemente počev od nekog slikaju u minimum skupa D, izuzimajući onu funkciju koja sve elemente domena slika u munimum skupa D. Postoji bijekcija između skupa N i skupa svih takvih funkcija. Ovo nema nikakve veze sa platonizmom, niti bilo kojim drugim pravcem u matematici. [ uranium @ 09.07.2005. 21:56 ] @
Code:
Zadatak 41:
Da li je moguće da neka firma bude "u minusu" svakih k uzastopnih meseci, ali da posle n>k
meseci bude "u plusu"? (k i n su unapred dati prirodni brojevi)
[Ovu poruku je menjao uranium dana 03.10.2005. u 00:11 GMT+1][ aleksandar88 @ 02.11.2005. 23:53 ] @
ako neko jos prati ovu temu a zna odgovor 7 zadatka(onaj sa bojom medveda)
neka ga posalje jer me interesuje resenje (ako je uopste vezano za matematiku).
Imam jedan zadatak koga sam cuo ranije i intersuje me da li ga neko moze resiti, zadatak glasi odprilike ovako:
Code:
Zadatak 42:
Covek je imao 20 ovaca, svaki dan je prodavao neparan broj istih i tako 5 dana zaredom.
Na kraju mu nije ostala ni jedna ovca. Kako je to izveo?
-koliko me secanje slizi.
Ako neko mozda zna pravu verziju ovog zadatak ili neki sa slicnom idejom neka ga posalje.
[Ovu poruku je menjao Bojan Basic dana 07.11.2005. u 15:16 GMT+1][ Bojan Basic @ 04.11.2005. 12:02 ] @
Tema se još prati, samo nisi precizirao na koji zadatak misliš. Postoje dva zadatka sa bojom medveda, jedan je Zadatak 6 koji je rešen na drugoj temi a ovde samo ostavljena postavka. Drugi zadatak sa bojom medveda je Zadatak 36 koji još uvek nije rešen u potpunosti ali dobar deo je otkriven (videti ovu poruku) pa eto prilike da svi još jednom razmislimo o tom problemu. [ Milos Stojanovic @ 04.11.2005. 22:29 ] @
Da nije plišani meda? ;)
[ Mikky @ 08.11.2005. 00:45 ] @
Odgovor na zadatak 36 - Medved je crno bele boje :)
[ noviKorisnik @ 08.11.2005. 09:00 ] @
Odgovor na 42 (odakle li poznat ovaj broj :-)))
Citat: Covek je imao 20 ovaca, svaki dan je prodavao neparan broj istih i tako 5 dana zaredom.
Na kraju mu nije ostala ni jedna ovca. Kako je to izveo?
Znamo svi da postoje bele ovce i crne ovce. Neparan broj belih i neparan broj crnih i tako manje-više pet puta... mora da bude paran broj. [ stf @ 11.11.2005. 18:34 ] @
Evo dva zadatka od mene:
Code:
Zadatak 43:
Rasporediti 19 tačaka tako da (bar) 9 redova sadrži tačno 5 tačaka.
Evo još jednog, malo lakšeg:
Code:
Zadatak 44:
Da li je moguće da 6 duži jednake dužine obrazuju 4 podudarna trougla? Kako?
[ nnn @ 11.11.2005. 19:07 ] @
Evo jedan meni zanimljv:
Code:
Zadatak 45
Putnik se nadje na racvanju puta na dva dela,
Tu stoje dva coveka od kojih jedan govori samo istinu, a drugi samo laze.
Kako ce da posle jednog pitanja sazna koji je pravi put?
[Ovu poruku je menjao noviKorisnik dana 11.11.2005. u 20:13 GMT+1]
[Ovu poruku je menjao nnn dana 12.11.2005. u 10:18 GMT+1][ qzqzqz @ 11.11.2005. 21:13 ] @
Resenje za 44: U pravilnom tetraedru imamo 6 duzi i 4 podudarna jednakostranicna trougla.
45. je poznat pa necu sad da se pravim pametan. :)
[ Andreja Dulovic @ 07.12.2005. 10:27 ] @
Resenja zadatka: 45
covek treba da postavi sledece pitanje: "kad bih ja pitao ovog pored tebe 'koji je pravi put', sta bi mi on rekao?" :) :)
[ dandelion @ 25.01.2006. 21:53 ] @
Ja do sad nisam odgovarala na vasa pitanja, ali sam ih kuci resavala. Ovo mi je dala drugarica pa mi se ucinilo zanimljivo
Code:
Zadatak 46:
Tvrtko sada ima dvostruko vise godina nego sto ih je imao Trpko kada je Tvrtko imao
onoliko godina koliko sada ima Trpko. Oni zajedno imaju 70 godina.
Koliko godina ima svaki od njih ?
[Ovu poruku je menjao Bojan Basic dana 03.03.2006. u 10:42 GMT+1][ Farenhajt @ 25.01.2006. 22:46 ] @
Citat: dandelion
Tvrtko sada ima dvostruko vise godina nego sto ih je imao Trpko kada je Tvrtko imao onoliko godina koliko sada ima Trpko. Oni zajedno imaju 70 godina.
Koliko godina ima svaki od njih ?
Ako Tvrtko sada ima  godina, a Trpko  godina, onda je Tvrtko imao  godina pre 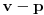 godina. Tada je Trpko imao  godina. Prema uslovu zadatka imamo sistem
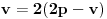
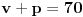
čije je rešenje 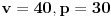 . [ dandelion @ 26.01.2006. 12:23 ] @
Citat: Farenhajt: Ako Tvrtko sada ima  godina, a Trpko  godina, onda je Tvrtko imao  godina pre 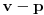 godina. Tada je Trpko imao 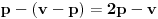 godina. Prema uslovu zadatka imamo sistem
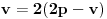
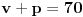
čije je rešenje 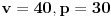 .
Ja sam malo drugacije ali mi je ovoliko ispalo!!! [ dandelion @ 26.01.2006. 12:26 ] @
Evo jos jedan zadatak
Code:
Zadatak 47:
Na pijacu se mora pazariti 20 komada jaja za 20 dinara! ima 3 vrste. od sve 3 vrste se
mora najmanje jedno kupiti.
Cene na komad: jaje od kokoske ima cenu od 50 para
jaje od patke 2 dinara
jaje od guske 3 dinara
resenje se mora u glavi naci u roku od 5 - 10 minuta
(bez olovke i racunara) !
[Ovu poruku je menjao Bojan Basic dana 03.03.2006. u 10:44 GMT+1][ braker @ 15.02.2006. 17:17 ] @
ogranichi na 1 min.14,5,1
[ sieben @ 29.03.2006. 22:25 ] @
Odgovor na zadatak 37.
da nije mozda sledeci broj u nizu -6
[ Bhamby @ 30.03.2006. 01:37 ] @
Ne.
[ Nedeljko @ 31.03.2006. 01:46 ] @
Bojane, još nisi postovao rešenje zadatka sa medvedom.
[ srki @ 31.03.2006. 03:34 ] @
Rec je o koali koji je bio na eukaliptusovom drvetu (posto se hrani eukaliptusom) pa je boja medveda siva. Ne znam za druge medvede koji se penju na tu visinu.
[Ovu poruku je menjao srki dana 31.03.2006. u 04:36 GMT+1]
[ stex @ 31.03.2006. 09:51 ] @
Medved je upao u rupu, nije pao.
[ srki @ 31.03.2006. 09:55 ] @
Da, ali upao je u rupu sa neke visine.
[ Bojan Basic @ 31.03.2006. 10:31 ] @
Citat: Nedeljko:
Bojane, još nisi postovao rešenje zadatka sa medvedom.
Ne volim da saljem resenja na zadatak koji ja postavim „tek tako“, volim da sacekam (cak i ako to ume da potraje) ili da neko resi ili da se neko javi i pita me da postujem resenje i onda cu ga rado poslati. Posto si trazio, evo resenja.
Uglavnom, Mikky je dao tacan odgovor, mada nije obrazlozio. Medved je crno-bele boje. Obrazlozenje je kao sto je srki rekao, samo se ne radi koali nego o pandi. Moze i koala, ali moram priznati da mi to nije palo na pamet, zadatak nisam smislio nego video i tamo u resenju pise samo panda. [ Farenhajt @ 31.03.2006. 11:36 ] @
Hm... Što se medveda tiče, proračun (ako ne grešim) daje da je pao s visine od oko 1,25 metara (tj. na početku pada nalazio se 1,25 m iznad otvora rupe), a s te visine mogu da padnu raznorazni medvedi - beli s neke ledene formacije, grizli s litice pored reke i slično... A s druge strane, pande jedu bambus u sedećem položaju, pošto je bambus suviše tanak da bi se oni penjali na njega... Tako da mi zvanično rešenje malo ne deluje ubedljivo. (Koale se pak lako penju i na znatno veću visinu.)
(Ako neko hoće da proveri račun, evo: pri 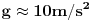 imamo da 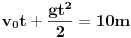 daje 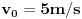 , a onda je 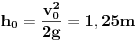 ) [ stex @ 31.03.2006. 14:08 ] @
Ne bih sad da pametujem ali zadatak je bio:
Code:
Medved pada u rupu dubine 10m i posle 1s udara u njeno dno. Koje je boje medved?
A na netu sam nasao:
Code:
A bear has fallen from a height of 10 meters.
It took square-root of 2 seconds for it to fall on the ground.
Now can you tell me the COLOR of the bear based on this information?
Ipak ima razlike, pasti sa visine od 10 m i pasti u rupu dubine 10 m.
[ AkvaMarina @ 31.03.2006. 18:34 ] @
Koala se penje po drvecu ali nije medved nego torbar. Jedino da je neko ubacio pandu u doticnu rupu :)
[ branchy @ 10.04.2006. 19:22 ] @
Odgovor na zadatak 37.
Da lli je sledeci broj u nizu -1?
[ istok77 @ 29.04.2006. 09:53 ] @
Citat:
A bear has fallen from a height of 10 meters.
It took square-root of 2 seconds for it to fall on the ground.
Now can you tell me the COLOR of the bear based on this information?
Otkad se square-root of 2 prevodi kao "jedan" ??????? [ Bojan Basic @ 29.04.2006. 12:07 ] @
@stex:
Našao si drugačiju postavku od one koju sam ja našao (i preveo). Evo kako glasi original koji sam ja koristio:
Code:
A bear falls into a hole in the ground. The hole is 10 metres deep. After one second
the bear reaches the bottom of the hole. What colour is the bear?
[Ovu poruku je menjao Bojan Basic dana 29.04.2006. u 13:12 GMT+1][ KPYU @ 30.04.2006. 02:40 ] @
Ni panda nije medved, već rakun. :)
[ Bojan Basic @ 30.04.2006. 10:32 ] @
Ne bih se baš kladio.
http://www.nature.ca/notebooks/english/gpanda.htm
Citat: The weight of evidence that has accumulated over the years, however, now supports the view that it is related to bears. Its closest relative is the spectacled bear of South America.
Takođe valja videti i ovu klasifikaciju:
http://animaldiversity.ummz.um....html#Ailuropoda%20melanoleuca
Iako se ovaj sajt ne uzima kao previše merodavan, nije zgoreg pogledati šta i tu piše.
http://en.wikipedia.org/wiki/Giant_Panda
Citat: However, genetic testing seems to have revealed that giant pandas are true bears and part of the Ursidae family. Its closest bear relative is the Spectacled Bear of South America.
Dakle, bilo je prilično mnogo nesuglasica, ali na kraju se panda ipak svrstava u medvede. [ Bhamby @ 30.04.2006. 15:06 ] @
Citat: #1111162/ branchy: Odgovor na zadatak 37.
Da lli je sledeci broj u nizu -1?
Ne. [ Zorzo @ 27.07.2006. 11:12 ] @
Evo jedan lagan zadatak od mene. Svidio mi se tekst.
Code:
Zadatak 48:
1.5 koka za 1.5 dana snese 1.5 jaja. Koliko 5 koka snese jaja za 7 dana?
[Ovu poruku je menjao Bojan Basic dana 25.08.2006. u 20:24 GMT+1][ maricn @ 06.08.2006. 20:20 ] @
da nije 33.3?
loL
[ ventura @ 06.08.2006. 20:30 ] @
Evo jednog lepog zadatka:
Dokazati da je P = NP
:)
[ Zorzo @ 07.08.2006. 10:11 ] @
Meni nije ispalo tako. Napiši postupak.
[ peka @ 23.08.2006. 01:26 ] @
Ja sam dobio 23,3. Jel to?
Postupak:
1,5 koka za 1,5 dana snese 1,5 jaja (1)
1 koka za 1,5 dana snese 1 jaje
1 koka za 3 dana snese 2 jaja
1 koka za 6 dana snese 4 jaja (2)
1 koka za 7 dana snese 4,66 jaja ( (2) + 0,66*(1) )
5 koka za 7 dana snese 23,33 jaja
[ Srdjan_pmf @ 25.08.2006. 19:22 ] @
Evo i par lakih zadacica od mene
Ovo bi trebalo svi da znaju...
Code:
Zadatak 49:
Nedaleko od morske obale usidrio se brod. Niz njegovu bocnu stranu vise merdevine od kanapa.
Merdevine imaju 10 stepenica. Rastojanje izmedju stepenica je 30 cm. Najniza stepenica dodiruje vodu.
More je mirno ali pocinje plima koja podize vodu svakog sata za 15 cm.
Posle koliko vremena ce voda dostici trecu stepenicu?
Code:
Zadatak 50:
Rep ribe je tezak 2kg, a glava onoliko koliko i rep i pola trupa; trup je tezak koliko glava i rep.
Koliko je teska riba?
Nisam siguran da li sam prave redne brojeve stavio tako da ako je greska molio bih moderatora da ispravi. [ Zorzo @ 26.08.2006. 16:41 ] @
Moje rešenje je 23.3
[ Zoran Milovanovic @ 26.08.2006. 17:21 ] @
Meni samo nije jasno kako koke mogu da snesu 1/3 jajeta... ali ako vi tako kazete :)
[ Srdjan_pmf @ 26.08.2006. 21:48 ] @
Nije poenta u jajima
Mogao je zadatak da bude npr tipa: Da neki radnici urade neki deo posla za neko vreme...
nije uopste moralo da bude sa kokama.
** Inace i moje resenje je 23,3
5 koka * (14/3) = 23,3
[Ovu poruku je menjao Srdjan_pmf dana 26.08.2006. u 23:01 GMT+1]
[ BREAK-ON-THROUGH @ 27.08.2006. 22:59 ] @
1.5 jaja/1.5 koka/1.5 dana=1.5/1.5*1.5 jaja/koka*dan(ovo je dakle merna jedinica)= 1/1.5 jaja/koka*dan
1/1.5 jaja/koka*dan * 5 koka * 7 dana(skrate se koke i dani)= 23 jaja, a svake trece sedmice ce biti 24 jaja!
[ BREAK-ON-THROUGH @ 27.08.2006. 23:02 ] @
Nikada nece voda da se pomeri do trece stepenice, sem ako se ne poveca teret ne brodu ili se probusi brod!!
[ Backy @ 30.08.2006. 17:44 ] @
rešenje zadatka 30 ( http://www.elitesecurity.org/p388684)
treba da kaže "ja lažem", jer je to iskaz za koji se ne može odrediti istinitost pa samim tim nije ni istinit ni lažan. čudi me da se ovoga niko nije ranije setio... [ BREAK-ON-THROUGH @ 30.08.2006. 22:51 ] @
Odgovor na 31. zadatak :
Ako su brzine i kornjace i zeca konstante onda ce posle nekog t zec sigurno stici kornjacu! Usled ovoga se taj interval moze predstaviti kao neka tacka T( T=100m/(Vz-Vk) Vk-brzina kornjace, Vz -brzina zeca) na brojevnoj pravi. Ako uzmemo bilo koju tacku T1 koja je levo od tacke T ,a na pozitivnom delu ose ,onda mozemo dodavati na brojevnu pravu tacku T2 koja ce biti jednaka T2=T1/T*(T-T1)+T1, i dalje mozemo ovako u beskonacnost ,po formuli
Tn=T1 / T * ( T - Tn-1 ) + Tn-1 i formirati konvergentni niz ,koji konvergira u tacki T, gde je tacka T i gornje ogranicenje i tacka nagomilavanja, a da bi se dogodilo preticanje mora se preci tacka T!
E sad, tacka T1 je vreme za koje zec predje 100m, a to je T1=100m/10*Vk, dok je
T=100m/(10*Vk-Vk)=100m/9*Vk, sto znaci da je T1 / T=9/10!
Dalje Vk odredjuje da ce se za to veme preci 10 puta manje od 100m tj. 10m , a to dalje znaci da ce uz isto Vz, proteci 1/10 vremena u odnosu na predhodno vreme i tako ce se na brojevnoj pravi formirati pomenuti konvergentni niz po gore navedenoj formuli!
[ rossonerct @ 27.09.2006. 20:15 ] @
50. zadatak
R-riba
r-rep
G-glava
T-trup
r = 2
G = r + 1/2 T
T = G + r = r + 1/2 T + r
R = G + T + r
R = r + 1/2 T + r + 1/2 T + r
R = 2 + 1/2 T + 2 + 1/2 T +2
R = 6 + T
G + r = 6
G = 6 - r
G = 6 - 2
G = 4
T = G + r
T = 4 + 2
T = 6
R = 4 + 6 + 2
R = 12
[ Srdjan_pmf @ 29.09.2006. 14:10 ] @
odgovor na zadatak sa ribom nije tacan.
tacan odgovor je 16
ali dobro si poceo samo sto si zaboravio da dodas jos jedan r posle reda
R = G + T + r
treba ti
R= r + 1/2 T + r + r + 1/2 T + r
i onda se dobije
G=6
T=G+r=8
r=2
R=16
[ vaderru @ 27.11.2006. 19:43 ] @
R=16, u pravu si.
[ sarge @ 13.12.2006. 09:51 ] @
upalim 2 sijalice sacekam 5 minuta ugasim jednu udjem u sobu ipipnem jedu od ove dve ugasene ako je vruca onda
je to ona koju sam upalio i ugasio . Ova hladna se pali preko ovog prekidaca koji nisam dirao . A ova upaljena je ona sijalica koju sam upalio
[ vojpet @ 12.02.2007. 12:13 ] @
Rešenje nije samo severni pol, već beskonačno mnogo krugova u blizini južnog pola. Ne znam da li tamo uopšte žive medvedi.
[ semiconductor @ 17.02.2007. 19:28 ] @
Jedan osudjenik je osudjen na cudnu kaznu.
Receno mu je da ce u toku naredne nedelje (od ponedeljka do nedelje)
biti pogubljen, ali tako da dan unapred nece znati kada ce to biti.
Zatvorenik je razmisljao:
- Nece me pogubiti u nedelju, jer ako me ne bi pogubili do subote,
ja cu vec u subotu znati da ce me pogubiti u nedelju, pa kako to vec znamo dan pogubljenja nije nedelja.
- Nece me ni u subotu pogubiti jer bih vec u petak znao da je subota dan pogubljenja.
- Ostaju mi dani od ponedeljka do petka.
- Nece me ni u petak pogubiti, jer bih vec u cetvrtak znao dan svog pogubljenja.
Ovakvim razmisljanjem zatvorenik stize do ponedeljka i zakljucuje da ga nece ubiti.
Zadovoljan i opusten u svojoj celiji cekao je kraj kazne.
Medjutim, u sredu dodjose dzelati i odvedose ga na pogubljenje.
Gde je greska u razmisljanju zatvorenika?
[ Daniel011 @ 18.02.2007. 19:14 ] @
Evo da pokušam sa nekim svojim razmišljanjem, pa i ako omašim, nema veze...
Po meni, razmišljanje "neće me ni u subotu pogubiti jer bih već u petak znao da je subota dan pogubljenja" je pomalo diskutabilno. Pretpostavimo da je osuđenik ostao živ do petka uveče. On bi tada rezonovao "ako me pogube u nedelju, ja ću dan unapred znati koji je dan pogubljenja, ali sa druge strane, ako nedelju iz tog razloga eliminišem kao mogući dan pogubljenja, onda ću isto tako i za subotu znati dan unapred (tj. večeras) da je to dan pogubljenja". I samim tim se kod osuđenika stvara doza neizvesnosti, tako da osuđenik neće moći sa apsolutnom sigurnošću da zna da će pogubljenje biti baš u subotu. Ova neizvesnost je sve veća kako se pomeramo za po jedan dan unazad, tj. prema ponedeljku.
[ semiconductor @ 18.02.2007. 21:33 ] @
Onda bi tom logikom najveca neizvesnost bila u ponedeljak.
Pogubili su ga u sredu.
[ Daniel011 @ 18.02.2007. 23:56 ] @
Tačno, najveća neizvesnost bi bila u ponedeljak. Ali ne vidim odakle taj zaključak, da ako je nekog dana najveća neizvesnost, tog dana mora biti izvršeno pogubljenje?
[ Zoran Milovanovic @ 19.02.2007. 00:25 ] @
E, ko ne zeli da cita gluposti, neka preskoci moj post :P
Kao prvo zaboravio je da osudjen na smrt. Samim tim on uopste nije ni razmisljao o pogubljenju, niti je pretpostavljao da ga ceka smrt. Samim tim mogli su ga ubiti i u nedelju ;) Jer je bio siguran da ga nece pogubiti!?
A ja uopste ne vidim sto je bitno da li je bila sreda ili bilo koji dan u nedelji.
A greska je u tome sto je poceo od kraja nedelje. Da je poceo da ispituje od ponedeljka, znao bi da je njemu svaki dan sem nedelje neizvesan.
[ semiconductor @ 19.02.2007. 21:56 ] @
LOL!
Ja bih pre zaboravio da dishem :)
[ Daniel011 @ 19.02.2007. 22:09 ] @
:)
Pa jesi li i sam rekao da je "zadovoljan i opušten u svojoj ćeliji čekao kraj kazne.";)
Šalu na stranu, da li znaš pravi odgovor na ovu zagonetku? Ne tražim da nam još uvek kažeš, jer možda nekome još neka ideja padne na pamet, samo me zanima da li je tebi rešenje poznato? [ semiconductor @ 20.02.2007. 11:37 ] @
Na ovaj zadatak sam slucajno naleteo.
Secam ga se iz matematickih listica (osnovna skola),
ali se ne secam razloga. Tako da ni ja ne znam odgovor.
P.S.
Provericu sve moje matematicke listice (da, jos ih cuvam) :)
Kad nadjem dacu odgovor.
[ Dahaka @ 07.05.2007. 16:48 ] @
{
Meni je bilo crnjak da citam ave ove strane pa sam dao odgovor po kome Ja mislim da je resenje za Zadatak 5:;
Upalimo prvi i drugu prekidac;
Odemo i vidimo koje sijalice rade;
Prva sijalica koja radi - prvi prekidac;
Druga sijalica koja radi drugi - prekidac ili srednji prekidac za srednju sijalicu;
Treca ne radi jer nije upaljen treci prekidac;
A imam i ovu;
Upalimo prvi i treci prekidac;
Odemo da vidimo sijalice;
Prva sijalica prvi prekidac;
Druda drugi tj. onaj sto nije upaljen;
I treca sijalica treci prekidac;
}
[ leptira @ 16.05.2007. 21:59 ] @
ovaj je zadatak već bio, ali g aniko nije riješio, a baš mi se čini zanimljiv zadatak.
Code:
Zadatak 24:
Majka je rodila sina sa 21 godinom. Za tačno 6 godina (računajući od danas), majka će
biti 5 puta starija od sina. Gde se trenutno nalazi sinovljev otac? [ Daniel011 @ 16.05.2007. 22:18 ] @
@leptira
Pretpostavljam da svi znamo rešenje, ali da niko, iz pristojnosti, nije hteo da ga objavi.  [ Farenhajt @ 16.05.2007. 22:21 ] @
Rešenje sistema
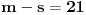
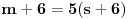
jeste 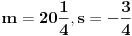 , što znači da je otac upravo u majci.
@Daniel: Može se to i pristojno sročiti  [ Dahaka @ 17.05.2007. 15:56 ] @
@leptira
@Daniel011
I da cujem resenje?
[ Damanalovca @ 27.05.2007. 09:31 ] @
Citat: Dahaka: @leptira
@Daniel011
I da cujem resenje?
Ima dva rješenja.
Ili je na ili ispod majke (normalno ako isljučimo varijacije na temu iz kamasutre) http://static.elitesecurity.org/winksquare.gif[ leptira @ 27.05.2007. 18:17 ] @
Code:
zadatak 51
_____________________
| | |
| | |
|__________|__________|
| | | |
| | | |
|__ ___|________|_____|
// ne izgleda baš najbolje, al hajd :)
povući krivu liniju tako da prolazi kroz svaku duž 'nacrtanog' predmeta samo jednom
[ dralle @ 27.05.2007. 20:37 ] @
NemogućE!
[ Dahaka @ 28.05.2007. 08:05 ] @
sasvim moguce.
Sada nemam skener ili foto pa ne mogu da Vam pkazem.
[ Zoran Milovanovic @ 28.05.2007. 10:43 ] @
Nacrtaj nam u Paintu :) Moze tako?
[ Farenhajt @ 28.05.2007. 12:03 ] @
Gornji levi, gornji desni i donji srednji pravougaonik oivičeni su sa po 5 duži, tako da je nemoguće - sem ako "duž" nije dobro definisana u postavci.
[ leptira @ 28.05.2007. 17:58 ] @
tačno tako. oivičeni su sa po pet duži. a svi kažu da su vidjeli rješenje ali da su zaboravili. ja sam to špokušavala i pokušavala i nikako. ako neko zna neka javi...
[ petarm @ 07.07.2007. 19:52 ] @
Bojan je u pravu po najnovijoj klasifikaciji Veliki panda spada u familiju Ursusa. Dok je Crveni panda zaista rakun :) Ali cak i da panda nije medved resenje bi bilo crno-bele boje. Postoji jedan meda koji se pentra po drvecu Sun bear (spada takodje u familiju Ursusa) koji je crn sa belinom na grudima :)
[ R A V E N @ 17.04.2008. 03:26 ] @
Code:
Zadatak 24:
Majka je rodila sina sa 21 godinom. Za tačno 6 godina (računajući od danas), majka će
biti 5 puta starija od sina. Gde se trenutno nalazi sinovljev otac?
Preletih tek površno ovu temu,pa imam ovaj komentar:
Ako je majka već rodila sina(dakle,prošlo vrijeme),kako to da je otac trenutno u aktu začetka tog sina sa majkom?
To je upravo kvaka(nedosljednost) koja dodaje začin kompleksnosti ovakvim zadacima - folovima. [ ingenerio @ 18.05.2008. 22:33 ] @
Code:
Zadatak 52.
Kako je ovo moguce (ili odakle ovaj kvadrat viska) ?
 [ braker @ 19.05.2008. 22:17 ] @
Ne moras ni racunati pojedinacne povrsine i uglove koje hipotenuze zaklapaju - sa same slike je ocigledno.
Uporediti mesto na donjoj slici gde se spajaju zeleni i crveni trougao sa istom tom tackom na gornjoj - odatle rupa.
[ ingenerio @ 21.05.2008. 16:21 ] @
Evo i kompletnog odgovora:
jednostavnom matematikom proizilazi da je zbir POVRŠINA tri geometrijska tela:
PRVA (GORNJA) SLIKA:
1. CRVENI trougao: P=12 kockica na kvadrat
2. ZELENI trougao: P=5 kockica na kvadrat
3. Žuto+zeleno telo: P=15 kockica na kvadrat
___________________________________
Što kad se sabere, iznosi P=32 kockica na kvadrat, a površina VELIKOG trougla iznosi 32,5 kockica na kvadrat!
DRUGA (DONJA) SLIKA:
1. CRVENI trougao: P=12 kockica na kvadrat
2. ZELENI trougao: P=5 kockica na kvadrat
3. Žuto+zeleno telo+prazan prostor: P=16 kockica na kvadrat
___________________________________
Što kad se sabere, iznosi P=33 kockica na kvadrat, a površina VELIKOG trougla iznosi 32,5 kockica na kvadrat!
Znamo svi da je potrebno da zbir površina svih tela u VELIKOM trouglu mora da bude jednaka površini VELIKOG trougla, ali to ovde nije slučaj, NEGO je taj zbir veći > ili manji < od površine velikog trougla! :o
ZAKLJUČAK JE da postoji jedna NELOGIČNOST, a to je da zbir svih geometrijskih tela koja se nalaze u velikom trouglu (i na slici 1 i na slici 2) N I J E jednaka površini velikog trougla!
A to je moguće JEDINO ako jedan ot tri trougla (crveni, zeleni ili VELIKI) zapravo nije trougao! :lol:
Ovo je čisto MATEMATIČKO rešenje!
EVO i drugog, malo slikovitijeg ali drugačijeg rešenja (mislim postupak je drugačiji)-rešenje je ponovo isto veliki TROUGAO nije Trougao! :lol:
 [ LW40 @ 04.06.2008. 20:46 ] @
Vidim da forum nije bas najaktivniji ali valjda ce neko probati da resi ovaj zadatak (ja ne znam nikako da ga resim) -
U kvadrat stranice 1 smešteno je 76 tačaka. Dokazati da postoji bar 4 tačke koje se mogu prekriti krugom poluprečnika 1/7    [ semiconductor @ 20.06.2008. 19:00 ] @
Da probam prethodni zadatak (ukoliko se dobro secam):
Ovo je Dirihleov princip.
Kvadrat podelimo na kvadratice i to uzimajuci 1/7 kao polovinu dijagonale.
Stoga, dijagonala kvadrata bi bila d=a*sqrt(2) odnosno, d=2r, pa kad zamenimo
dobijemo da je stranica kvadratica oko 0.2. Znaci, delimo kvadrat na 5x5 (ovo 0.2*5=1 za stranicu kvadrata).
Tako smo dobili 25 kvadratica.
Ako bi u svaki kvadratic stavili po tri tacke, ukupan broj tacaka bi bio 75. Ostaje nam jedna tacka da je
postavimo u bilo koji kvadratic i on ce sadrzati 4 tacke. Kako kvadratic sadrzi 4 tacke, tako ce i opisana
kruznica sadrzati 4 tacke. Znaci postoji bar jedan krug koji zadovoljava uslov.
[Ovu poruku je menjao semiconductor dana 22.06.2008. u 09:28 GMT+1]
[ semiconductor @ 01.07.2008. 14:18 ] @
Hajde, hajde... znam da je leto...
Da vas malo "zagrejem" :)
Soba 12m x 12m x 30m. Pauk se nalazi na sredini manjeg zida (12 x 12) na jedan metar od plafona.
Muva se nalazi na suprotnom zidu na jedan metar od poda.
Koje je najkrace rastojanje koje pauk mora da predje kako bi uhvatio muvu, ali da ne plete mrezu?
Muva se ne pomera.
Pauk i muva se nalaze na osencenim zidovima.
Ah, da! Zaboravio sam da kazem da resenje nije 42m. [ zzzz @ 01.07.2008. 15:07 ] @
= 40m
[ semiconductor @ 02.07.2008. 10:16 ] @
Tacno! Jesi li znao ili si izracunao? Postupak bi bio pozeljan (i skica).
[ zzzz @ 02.07.2008. 12:28 ] @
Koja skica treba?Lijeva ili desna?
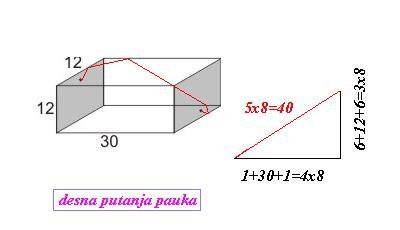
Dobro evo desna.To je kad pauk ide ukoso ka gore al na desno.
[Ovu poruku je menjao zzzz dana 02.07.2008. u 18:29 GMT+1][ semiconductor @ 02.07.2008. 16:35 ] @
Pa, valjda si crtao nekakvu skicu. U svakom slucaju, napisi kako si izracunao.
[ zzzz @ 02.07.2008. 19:51 ] @
Važno je da se pauk uvijek drži istog ugla skretanja arctg(0.75).Znači ne pravo
ka plafonu već ukoso pod ovim uglom.Tako isto na plafonu, udaljenijem zidu, podu
i na kraju zidu na kom je muva.
[ Vincenity @ 03.07.2008. 16:47 ] @
Fora je valjda da nacrtas mrezu tela...
Kad nacrtas sve moguce mreze, kojih nema puno, povuces prave linije od jedne do druge tacke. Te linije su sigurno najkraca rastojanja. I na kojoj mrezi dobijes najmanje to je najmanje moguce. I lako se dobije 40. Pitagorina teorema.
Jos da znam da crtam ovde sve bih prilozio...
[ semiconductor @ 03.07.2008. 19:22 ] @
Upravo tako. Resenje je u svakom slucaju tacno. Naravno, ja sam mislio
na mrezu kvadra (prizme) kada sam spomenuo skicu, ali nema veze.
Hajde da se vratimo na Dirihlea mada je prosto :)
Tepih 4m x 4m progrizli moljci na 15 mesta. Dokazati da se moze iseci
deo tepiha od 1m x 1m bez rupe. Ne mora skica :)
[ zzzz @ 04.07.2008. 00:38 ] @
Citat: semiconductor:Hajde da se vratimo na Dirihlea mada je prosto :)
Tepih 4m x 4m progrizli moljci na 15 mesta. Dokazati da se moze iseci
deo tepiha od 1m x 1m bez rupe. Ne mora skica :)
Kako je ovo prosto?Odakle da počnemo kad neznamo kolike su rupe od moljca.Ako
su oblika kružnog, jednake i prečnika 0.1m?Ili da idemo mjeriti moljca, pa da znamo
da je upravo tolika rupa, naprimjer 3 mm. [ semiconductor @ 04.07.2008. 11:26 ] @
Da, da, u pravu si... izostavio sam taj podatak.
Rupe su zanemarljive velicine.
Cim si to primetio, verovatno vec znas resenje :)
[ sanja2010 @ 04.07.2008. 13:42 ] @
Ih... kad niko nece :) Izdelimo polje na kvadrate 1x1, imamo 16 kvadrata, a 15 rupa, pa nam ostaje jedno parce metar puta metar bez rupe :)
[ zzzz @ 04.07.2008. 16:53 ] @
Meni se čini da bi i u slučaju 16 rupa mogli izvući neki kvadrat 1mx1m bez rupe ma
kako te rupe bile razbacane.Podrazumjeva se da se kvadrat smije zarotirati.Samo
ovo trebam dokazati.Zna li neko?
[ Bojan Basic @ 04.07.2008. 18:11 ] @
Zzzz, nisi u pravu. Pogledaj sliku (crne tačke su rupe od moljaca, dok su plave čvorovi celobrojne mreže, radi lakšeg snalaženja).
[att_img]
[ zzzz @ 04.07.2008. 18:56 ] @
Ako imaš koordinate tačaka pa da probam.Inače na ovakvoj slikici lako uglavljujem
kvadeat.
 [Ovu poruku je menjao zzzz dana 04.07.2008. u 20:20 GMT+1]
[Ovu poruku je menjao zzzz dana 04.07.2008. u 20:20 GMT+1][ Bojan Basic @ 04.07.2008. 20:03 ] @
Kvadrati koje si uglavio imaju stranicu manju od  .
Uzmimo da je donje levo teme velikog kvadrata u koordinatnom početku, i neka rupe čine kvadratnu mrežu stranice 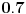 , pri čemu donja leva rupa ima koordinate  . Stranica tvog zelenog kvadrata mora (očito) biti manja od dijagonale najmanjeg kvadrata mreže koju obrazuju rupe, što je 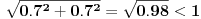 . Lako se pokazuje da je plavi kvadrat u još goroj situaciji. [ semiconductor @ 04.07.2008. 21:21 ] @
Ljudi... Za Dirihleov princip se uvek uzima najnepovoljniji slucaj,
U ovom slucaju bi to bio da su moljci progrizli tepih u okviru svakog kvadratnog metra.
Ako je ovo slucaj, ostaje nam jedan kvadratni metar celog tepiha.
Ostale varijante su npr. da su moljci progrizli svih 15 rupa u jednom kvadratnom metru tepiha.
Tada imamo cak 15 tepiha od 1m x 1m.
Nema potrebe dalje zalaziti u analize sta bi bilo kad bi bilo, jer kao sto rekoh ovde se
trazi najnepovoljnija varijanta i ne znamo gde su moljci progrizli.
[ Bojan Basic @ 04.07.2008. 21:25 ] @
Ako pročitaš poslednje nekoliko poruka, videćeš da pričamo o sasvim drugom zadatku (koji je započeo zzzz).
[ semiconductor @ 05.07.2008. 00:26 ] @
Video sam. Zato sam i napisao ovo prethodno. Mi ne znamo gde su rupe.
Polazimo od toga da iskoristimo celu povrsinu tepiha. Rotiranjem kvadrata
ne mozemo dobiti istu povrsinu jer ima ostataka u materijalu.
[ Bojan Basic @ 05.07.2008. 00:44 ] @
Negde se debelo ne razumemo. Postavio si zadatak koji zahteva dokaz da se pored petnest rupa uvek može naći neoštećen kvadratni metar, i to je brzo rešeno (rešila je Sanja). Zatim je zzzz pretpostavio da se čak i ako je tepih progrizen na šesnaest mesta opet može naći kvadratni metar bez rupa, i pitao je može li neko to dokazati (ili opovrgnuti) — dakle, to je sasvim drugi zadatak, i nema veze sa Sanjinim rešenjem. Pokazao sam da njegova pretpostavka nije tačna, tj. da se od tepiha sa šesnaest rupa raspoređenih kao na mojoj skici ne može iseći neoštećen kvadratni metar.
[ semiconductor @ 05.07.2008. 15:48 ] @
Ma, razumemo se mi. Evo sta pokusavam da kazem...
Ako je tepih  , a imamo 16 rupa, to
znaci da u najgorem slucaju svaki kvadratni metar tepiha
sadrzi po jednu rupu. U slucaju rotiranja kvadratnog metra,
iskoristiva povrsina tepiha se smanjuje i sasvim je sigurno
da necemo naci taj jedan deo 1mx1m tepiha bez rupe. [ Bojan Basic @ 05.07.2008. 18:58 ] @
Sad sam ukapirao šta pokužavaš da kažeš, ali ti poruka nema nikakvog osnova. Prvo, da bi u matematici koristio izraze poput „najgori slučaj“, moraš strogo pokazati da je najgori slučaj stvarno to što tvrdiš. Drugo, tvoja definicija „najgoreg slučaja“ uopšte nije jednoznačna (jer se po jedna rupa u svakom jediničnom kvadratu može postići na više načina); dobro, pretpostavićemo da svaki od tih rasporeda proglašavaš najgorim. Treće, i najbitnije, uopšte nisi u pravu: ako je šesnaest rupa raspoređeno tako da se u centru svakog jediničnog kvadrata nalazi po jedna, to ispunjava tvoj kriterijum „najgoreg slučaja“, a iako se ne može smestiti „prav“ kvadrat, rotiran za 45° smeštaš bez problema.
[ galet@world @ 10.07.2008. 08:27 ] @
Nekad je bila vrlo popularna Mađarska kocka, a ja sam iz „patriotskih razloga” hteo da uzvratim mojom zagonetkom „Srpski cvet”,ali su bili slabi izgledi da to neko i napravi, pa sam pokušao da napišem program,
a o programiranju nisam imao bledog pojma. Kupio sam neku knjigu za Q basic i nekad davno ispetljao ovaj
program koji sad prilažem. Možda može biti zanimljivo.Možda ovo i ne spada u ovu temu, a možda bi moglo
biti i posebna tema ili možda ništa od svega toga – neka odluči moderator.
[ semiconductor @ 11.07.2008. 01:48 ] @
Da li su svi krugovi razlicitih boja? Ako ih ima 7, onda ne moze da se dobiju krajevi "cveta".
Na ovom crtezu u Wordu ima ih mnogo vise. Razjasni malo.
[ galet@world @ 11.07.2008. 10:26 ] @
Krug je površina unutar kružnice. Očigledno je da bilo koji krug ne može biti u istoj boji.
U najboljem slučaju krug je "ofarban" sa tri boje kao na slici - centralni krug - latice su
u jednoj boji, međuprostori u drugoj i "krajevi" ili periferijske latice u trećoj.
Naravno, krugovi mogu sadržavati i više različito razvrstanih boja, ali traži se određen
raspored.
Cilj se, na primer, sastoji u sledećem - dovesti cvet u početno stanje, ako si proizvoljnim
okretanjem krugova razmestio latice i međuprostore tako da odmah ne vidiš šta treba
da uradiš (kako da okrećeš krugove) da bi ih doveo u početno stanje.
Isto kao kod kocke samo, čini mi se, malo teže jer su ovde "upetljani" i međuprostori.
Kod kocke su u pitanju samo kvadrati određene boje, ali, ako si je nekad "sastavljao"
i uspeo da je dovedeš u početno stanje - ipak se postavlja pitanje da li si to i zaista uradio
jer na sitnim kvadratičnim površinama kocke nema oznaka koje definišu orijentaciju
jednobojnih kvadratića u odnosu na neki od šest centralnih kvadratića kocke - tako da
može da izgleda kao da si doveo kocku u početno stanje, a ustvari verovatno nisi.
Da li je moguće i Srpski cvet dovesti u "početno stanje" sa orijentacijom latica i međuprostora
koja se razlikuje od orijentacije u početnom stanju - ne znam!
Treba otkriti, ali zasad neka to nije uslov.
[ R A V E N @ 17.07.2008. 01:29 ] @
Code:
Zadatak 53:
Posjedujemo naranču koja je pravilnog loptastog oblika,dakle ni na jednom mjestu nema ispupčenja,udubljenja ili rezova.Napravimo rez od vrha naranče(pod vrhom se smatra mjesto gdje naranča raste) ka dnu i kroz taj rez izvučemo unutrašnjost naranče.Kakvog će oblika biti površina preostale kore naranče?
Naivan trik-zadatak by myself(nešto se tekst razvuče). [ galet@world @ 17.07.2008. 21:51 ] @
Koja kora je preostala, a koja nije?
[ zzzz @ 17.07.2008. 23:47 ] @
Imaće oblik otpatka zgodnog za baciti u smeće i sa licem unutra, a naličjem okolo.
[ galet@world @ 18.07.2008. 17:47 ] @
površina "preostale" kore
Koje značenje (po tvom mišljenju) ima reč "preostale"?
Da li je moglo i bez te reči ili nije?
Pod pojmom "preostati", ja, na primer, podrazumevam ostatak nečega što nije "uzeto" ili nije "upotrebljeno" do kraja.
već predstavlja višak ili ostatak.
Ako se tako shvati reč "preostati" onda joj u tvom zadatku nema mesta jer je kora kompletna i nema "preostalog" dela
bez obzira na to što je rasečena.
[ R A V E N @ 27.07.2008. 04:45 ] @
Moglo je bez riječi.
Smisao riječi "preostati" je to da nam je od interesa samo kora,sadržaj naranče je nevažan i otišao je "sa scene".
[ mjux @ 10.01.2009. 03:57 ] @
Code:
Zadatak 54.
Bio jedan covek koji je radio u banci. Imao je zenu koja je srcani bolesnik i pila je lekove.
Jednog dana bankar dobije zaduzenje da odnese neki novac u filijalu njegove banke u drugom gradu.
Imao je voz koji polazi u 7 ujutru pa je zamolio zenu da ga probudi u 6.
Sledeci dan zena ga je probudila kako su se i dogovorili, on se istusirao, popio sa zenom kafu spremio se i krenuo na voz.
Zena se vratila u krevet da spava i sanjala je da joj je neko presreo muza i opljackao ga posto je nosio pare sa sobom.
Bankar je upao u saobracajnu guzvu ili sta vec, i sve u svemu propusti on taj voz i sta ce kuda ce, ide on nazad kuci.
Dolazi do vrata proba da otkljuca ali zena kako je on izlazio zakljuca vrata sa unutrasnje strane i zaboravi da izvuce kljuc, tako da on nije mogao da otkljuca.
Bankar pozvoni na vrata i zena se probudi i krene prema vratima da otvori. Dodje do vrata otkljuca, i kad je ugledala muza dozivi infarkt i padne mrtva.
Sta je nelogicno u ovoj prici????
i odma da dodam, odgovori nisu da nije popila lekove, kako on nosi pare sam, kako nije mogao da otkljuca, sto nije cekao drugi voz, i te varijante, sta vise ocigledno je i nije pa sad razmisljajte [ Daniel011 @ 10.01.2009. 10:40 ] @
Meni je nelogično kako može biti poznato šta je sirota žena sanjala neposredno pre svoje smrti, ako nije imala kome da ispriča taj svoj san. Znam da se obdukcijama može utvrditi štošta, ali baš i snovi... Hmmm...  [ ptak 13. @ 11.01.2009. 19:51 ] @
Evo jednog zadatka,zadaak sam cuo od veselinovica ( nick sa Es-a ) a zajendno smo nasli dva resenja....
Code:
Zena kuva rucak, i uzme vaz sa slju i hoce da sipa so u serpu, u kojoj kuva. Slucajno joj se omakne vaz iz ruke i u serpu uleti 200g soli, ona kuva nesto u vodi naravno...so se sad pomesala sa vodom i nema nazad :) Sad veselinovic i njegova zena jedu, jedu to sto je ona kuvala, i pored tih 200g soli greksom sipanih, veselinovic trazi slanik da posoli jelo, kaze neslano je....
Pitanje je sta su veselinovic i njegova lepsa polovina jeli :D ?
P.S. Nema resenja tipa prosula je vodu, i sl...znaci samo jelo je bitno, sta su jeli.....  [ marko1981 @ 11.01.2009. 20:11 ] @
Jaja?
[ marko1981 @ 11.01.2009. 20:24 ] @
Pasulj u serpi od 50L?
[ ptak 13. @ 11.01.2009. 22:29 ] @
Da ovo jetacan odgovor, jos jedan moguci je skoljke...dobro one se ne kuvaju ali je moguce...jaja su najlogicnija....
E sad veselinovic rece da ima jos neko resenje ako je tacno dopisacu....
Ovo nije tacno, odnosno moguce to je 4g soli po litru ili kilu pasulja, ali ne uzimamo u obzir 
[ ptak 13. @ 11.01.2009. 22:43 ] @
Evo jos jednog zadatka davno sam ga procitao negde...sigurno kad sam bio 5-6 razred iz nekog matemateskopa ili nesto sl. :)))))
Citat:
Izvrsen je zlocin u nekoj kancelariji. Inspektor kriminalistike ulazi u kancelariju sa ciljam vrsenja uvidjaja. Na stolu nalazi coveka kako sedi a gornjim delom tela lezi na stolu. Pored njega na stolu dosta papira, razbacanih olovki, sve to pomalo umrljano krvlju, i na stolu se nalazi i jedan kasetofon. Inspektor prilazi, nista ne pipa i vidi da je pucanj bio u glavu. U desnoj ruci ubijenog stegnut stoji crni pistolj. Jedna caura je pored stolice. Inspektor sve to gleda i dalje bez pipanja i nekako mu paznju privuce radio/kasetofon. Pogleda pazljivo i uvidja da je kasetofon ukljucen u striju. Kroz umetak za kasetu primecuje da se unutra nalazi kaseta. Pritiska dugme "PLAY" i na kasetofonu se cuje sledece. " Nisam vise mogao da izdrzim ovako". Zatim se zacuje pucanj.
Posle ove slike Inspektor pusta u kancelariju forenzicare a on u izvestaju zakljucuje da je u pitanju Ubistvo a ne Samoubistvo.
Moje pitanje je naravno na osnovu cega je to zakljucio ?
Resenje cu verovatno otkriti, ali svima kojima sam ga postavio jos niko nije dao resenje, znaci pokusajte. Ovo je po meni zadatak na dohvat mozga, samo ga treba ukljuciti. Neverovatno je to koliko volim Poara, Agatu Kristi, Serloka Holmsa....hehehe
pozdrav ! ! ! [ Jbyn4e @ 11.01.2009. 22:47 ] @
Pasulj sa kobasicom u limenci (samo podgrejati)? :)
Opet, postavlja se pitanje, ako je kuvala
a) jaja
b) skoljke
c) ovo sto sam napisao
koji ce joj moj so u sva tri slucaja? Tj. zasto bi uopste (osim ako nije maloumna) solila tako nesto?
[ Jbyn4e @ 11.01.2009. 22:53 ] @
A sto se tice ovog koji mi je upao izmedju odgovora...
Ako je inspektor pustio play, i cuo onoo sto je cuo, to bi znacilo da je neko vec premotao kasetofon unazad. Posto se vec cuo pucanj, tesko da je to mogao biti ubijeni - znaci neko drugi je to uradio. Ovo bi bilo da je inspektor zakljucio to sto je zakljucio forenzicar.
Opet, posto nije zakljucio forenzicar, jedino sto mi pada na pamet je da je forenzicar znao da je ubijeni levoruk.
Lazem, pada mi na pamet, da je pucanj u glavu negde gde ne moze da se "samoubije" (npr. celo? potiljak?).
[ marko1981 @ 11.01.2009. 22:53 ] @
Citat:
Izvrsen je zlocin u nekoj kancelariji. Inspektor kriminalistike ulazi u kancelariju sa ciljam vrsenja uvidjaja. Na stolu nalazi coveka kako sedi a gornjim delom tela lezi na stolu. Pored njega na stolu dosta papira, razbacanih olovki, sve to pomalo umrljano krvlju, i na stolu se nalazi i jedan kasetofon. Inspektor prilazi, nista ne pipa i vidi da je pucanj bio u glavu. U desnoj ruci ubijenog stegnut stoji crni pistolj. Jedna caura je pored stolice. Inspektor sve to gleda i dalje bez pipanja i nekako mu paznju privuce radio/kasetofon. Pogleda pazljivo i uvidja da je kasetofon ukljucen u striju. Kroz umetak za kasetu primecuje da se unutra nalazi kaseta. Pritiska dugme "PLAY" i na kasetofonu se cuje sledece. " Nisam vise mogao da izdrzim ovako". Zatim se zacuje pucanj.
Posle ove slike Inspektor pusta u kancelariju forenzicare a on u izvestaju zakljucuje da je u pitanju Ubistvo a ne Samoubistvo.
Moje pitanje je naravno na osnovu cega je to zakljucio ?
Pa morao je neko da pritisne "rewind" :) [ ptak 13. @ 11.01.2009. 22:56 ] @
Zasto soli....e decko slab si kuvar :D Salim se
Ako su jaja u pitanju. Dok se kuvaju obicno se u vodu stavi kasicicasoli da se ljuska ne bi raspukla, pitaj neke kuvarce kuvare i eci ce ti isto, neki stavljaju i sirce valjda.....:))))Ali za so sam 100% siguran
Ako su skolljke onda se takodjestavjla jer skoljka oce daispuca i mozes se poceci nije drugo, pa se takodje malo po soli, kakve veze ima so ne znam da objasnim ali ima....keva mi je od svoje 20-e godien kuvarica i radila je mnogo po Crnoj gori pa Holandiji pa Srbiji....mahom hoteli i eksklusivni restorani i zna te fore, ona to bas onako komplikovao objasni meni ali bolje da ti to ne pisem :D
A za ovaj tvoj pasulj....kako podgrejati bre, samo limenku na ringlu :D....aj pojasni....
P.S. Evo mnogo lepseg zadatka....gore....:))))
[ ptak 13. @ 11.01.2009. 23:04 ] @
He he he
@Jbyn4e , marko1981
Svaka casta, bravo. neverovatno je da ste tako brzo provalili foru, mnogi pre vas nisu uspeli. Da to je resneje premotana je traka....aj ako se sad setim jos nekog napiscu.....zanimljivi ste likovi, svaka cast....:))))))
[ Bojan Basic @ 15.01.2009. 11:29 ] @
Citat: ptak 13.:
Izvrsen je zlocin u nekoj kancelariji. Inspektor kriminalistike ulazi u kancelariju sa ciljam vrsenja uvidjaja. Na stolu nalazi coveka kako sedi a gornjim delom tela lezi na stolu. Pored njega na stolu dosta papira, razbacanih olovki, sve to pomalo umrljano krvlju, i na stolu se nalazi i jedan kasetofon. Inspektor prilazi, nista ne pipa i vidi da je pucanj bio u glavu. U desnoj ruci ubijenog stegnut stoji crni pistolj. Jedna caura je pored stolice. Inspektor sve to gleda i dalje bez pipanja i nekako mu paznju privuce radio/kasetofon. Pogleda pazljivo i uvidja da je kasetofon ukljucen u striju. Kroz umetak za kasetu primecuje da se unutra nalazi kaseta. Pritiska dugme " PLAY" i na kasetofonu se cuje sledece. " Nisam vise mogao da izdrzim ovako". Zatim se zacuje pucanj.
Posle ove slike Inspektor pusta u kancelariju forenzicare a on u izvestaju zakljucuje da je u pitanju Ubistvo a ne Samoubistvo.
Moje pitanje je naravno na osnovu cega je to zakljucio ?
Priča je i previše „nameštena“. Izmenio bih samo jedan detalj, što više ne dozvoljava rešenje koje su ponudili Jbyn4e i marko1981, a logično objašnjenje i dalje postoji: Citat: Izvrsen je zlocin u nekoj kancelariji. Inspektor kriminalistike ulazi u kancelariju sa ciljam vrsenja uvidjaja. Na stolu nalazi coveka kako sedi a gornjim delom tela lezi na stolu. Pored njega na stolu dosta papira, razbacanih olovki, sve to pomalo umrljano krvlju, i na stolu se nalazi i jedan kasetofon. Inspektor prilazi, nista ne pipa i vidi da je pucanj bio u glavu. U desnoj ruci ubijenog stegnut stoji crni pistolj. Jedna caura je pored stolice. Inspektor sve to gleda i dalje bez pipanja i nekako mu paznju privuce radio/kasetofon. Pogleda pazljivo i uvidja da je kasetofon ukljucen u striju. Kroz umetak za kasetu primecuje da se unutra nalazi kaseta. Premota je malo unatrag, pritiska dugme "PLAY" i na kasetofonu se cuje sledece. " Nisam vise mogao da izdrzim ovako". Zatim se zacuje pucanj.
Posle ove slike Inspektor pusta u kancelariju forenzicare a on u izvestaju zakljucuje da je u pitanju Ubistvo a ne Samoubistvo.
Moje pitanje je naravno na osnovu cega je to zakljucio ? [ ptak 13. @ 15.01.2009. 14:13 ] @
Pa sad si ti mene malo zavrnuo :))))) Mozda zato sto je "malo premotao unatrag" znaci ubica je snimio leposve i onda stopirao traku....? Da ili ne, razmisljacu i dalje....onda moze jos jedno resenje, traka nije stigla do kraja a da je stigla onda bi to vec bilo moguce da je u pitanju samoubistvo, znaci nema ko da stopira traku....mozda bi jos snimala ili se skroz izmoala, pa je morao celu da je premota.....nadam se da razumete :)))
Poz
[ Daniel011 @ 15.01.2009. 15:56 ] @
Da nije možda pištolj bio sa prigušivačem?
[ zzzz @ 16.01.2009. 00:00 ] @
Citat: Daniel011: Da nije možda pištolj bio sa prigušivačem?
Ja mislim da nije, jer bi se onda snimio na kasetu samo neki prigušeni "paf".
A to mu ga dođe kao da se ispija šampanjac.
!Pogađaj ponovo! [ ptak 13. @ 16.01.2009. 00:05 ] @
Ajde ovaj da probte resiti....
Stari kaludjer je imao krst sacinjen od 16 dragih kamenova. Svakoga jutra je brojao da vidi da li je svaki dragi kamen na svome mestu. Nesrecaje bila u tome sto stari kaludjer nije znao da broji vise od broja 10. Svako jutro je brojao 3 puta po 10 i to:
Odozdo do vrha
Odozdo na desnu stranu
Odozdo na levu stranu
Jednoga dana lukavi lopov koji je posecivao manastir, ukrade mu dva draga kamena. Kaludjer je i sledeceg dana brojao 3 puta po 10 na svoj nacin i nije primetio da mu nedostaju dva draga kamena.
Kako je to lopov sa krsta skinuo dva draga kamena ( krst je bio napravljen od tih dragih kamena na platnu ), a da kaludjer nije ni primetio.
Slika postojeceg krsta

[ Daniel011 @ 16.01.2009. 00:13 ] @
Citat: zzzz: Ja mislim da nije, jer bi se onda snimio na kasetu samo neki prigušeni "paf".
Pa upravo zato i pitam. Ako je na pištolju prigušivač, a na snimku se čuje pucanj, to bi inspektoru bio dovoljan podatak da zaključi da je tu nešto namešteno.
@ptak 13.
[att_img] [ ptak 13. @ 16.01.2009. 00:35 ] @
Da da, Danijel je ukrao dva draga kamena kaludjeru  [ zzzz @ 16.01.2009. 01:16 ] @
Meni izgleda da Danijel nije ukrao zlatnik već ga je dodao iz svog džepa.
Na onom donjem vertikalnom štapu ih je bilo šest a sad ih ima sedam.
[ ptak 13. @ 16.01.2009. 01:25 ] @
^Au druze, aj broji zlatnike da vidis da li ih je dodao....da nisi ti vlasnik zlatnika  [ Daniel011 @ 16.01.2009. 01:38 ] @
Da obrazložim kako sam ukrao dva draga kamena kaluđeru.:-) Kaluđer ih je imao 16, posle krađe ih ima 14. Pošto odozdo do vrha treba da ih izbroji 10, znači da po vertikali njihov broj treba da ostane nepromenjen posle krađe, tj. deset. Preostala četiri draga kamena treba da se nalaze na levoj i na desnoj strani. Pošto je krst simetričan, na levoj i na desnoj strani treba da ih bude jednak broj, odnosno po dva na svakoj strani. Da bi kaluđer odozdo na levu stranu izbrojao deset komada, ta dva draga kamena treba postaviti na levu stranu kod osmog dragog kamena, kada se broji odozdo. Isto važi i za desnu stranu.
[ galet@world @ 16.01.2009. 08:32 ] @
Citat: Premota je malo unatrag, pritiska dugme "PLAY" i na kasetofonu se cuje sledece. " Nisam vise mogao da izdrzim ovako". Zatim se zacuje pucanj.
Posle ove slike Inspektor pusta u kancelariju forenzicare a on u izvestaju zakljucuje da je u pitanju Ubistvo a ne Samoubistvo.
Moje pitanje je naravno na osnovu cega je to zakljucio ?
Ako je premota "malo" unatrag i posle pritiska na dugme "PLAY" se čuje rečenica i pucanj to znači da je kasetofon
isključen pre nego što se traka premotala do kraja odnosno pre nego što se kasetofon sam isključio.
Svaka traka ima na početku i na kraju jedan poduži neaktivni deo koji ne može da snimi zvuk. Ako bismo iz krajnjeg
sasvim premotanog položaja trake premotali traku "malo" unazad pa pritisli "PLAY" ne bi čuli ništa.
(Mogao je inspektor i odmah da pritisne "PLAY" pa da vidi da li se traka još premotava)
[Ovu poruku je menjao galet@world dana 16.01.2009. u 09:43 GMT+1][ Bojan Basic @ 16.01.2009. 13:49 ] @
Galet@world je tačno odgovorio (a nešto slično je prethodno napisao i ptak 13, ali nisam baš najbolje razumeo je li na to mislio).
[ Daniel011 @ 16.01.2009. 17:21 ] @
Ali snimljena poruka sa pucnjem se mogla nalaziti i pri samom kraju te strane kasete (jer u tekstu nigde nije eksplicitno naglašeno da kaseta nije pri kraju), tako da se par sekundi posle pucnja, kasetofon mogao i sam isključiti kad dođe do kraja strane (autostop mehanizam). U tom slučaju bi zaista bilo dovoljno da inspektor premota kasetu malo unazad, čuje poruku i ništa ne posumnja, ne?:-)
[ ptak 13. @ 19.01.2009. 23:42 ] @
Citat: Bojan Basic: Galet@world je tačno odgovorio (a nešto slično je prethodno napisao i ptak 13, ali nisam baš najbolje razumeo je li na to mislio).
Da i ja sam na to mislio ali nisam bas najbolje objasnio....  )))))sorry
Citat: Daniel011: Ali snimljena poruka sa pucnjem se mogla nalaziti i pri samom kraju te strane kasete (jer u tekstu nigde nije eksplicitno naglašeno da kaseta nije pri kraju), tako da se par sekundi posle pucnja, kasetofon mogao i sam isključiti kad dođe do kraja strane (autostop mehanizam). U tom slučaju bi zaista bilo dovoljno da inspektor premota kasetu malo unazad, čuje poruku i ništa ne posumnja, ne? 
E sad je suvise diskutabilan zadatak....i ovo se moze uzeti u obzir ali vec duboko udjosmo u zadatak..
---------------------------
Evo sad jos jedan onako da se ne dosadjujete....  )))
Pre svega da kazem da sam ja provalio mnogo dugu kombinaciju menjanja sudova i vina, naime resio sam zadatak sa 16 premetanja....ako sam dobro izbrojio. Eto to je mala pomoc, a evo zadatka
Code:
U balonu od 16L, nalazi se 16L vina. Podelite vino na dva jednaka dela, ako posedujete balone od 11 i 6 litara.
Aj da vidim ko je dobar matematicar, nemate vage i sl....samo sudove  )))) [ Daniel011 @ 21.01.2009. 12:19 ] @
Najkraće moguće rešenje je u 14 koraka:
[att_img]
[ ptak 13. @ 21.01.2009. 14:55 ] @
Da da da, to je najkarece moguce resenje izgleda....aj kasnije cu da vidim da postavim jos neki zadatak, onako zanimljiv :))))ovo nije bas zanimljivo bilo sa vinom.
[ ptak 13. @ 24.01.2009. 17:18 ] @
Imate dva kanapa koji kada se zapale gore tačno po sat vremena! Međutim, oni ne gore ravnomerno, što će reći da po dužini ne možete odrediti koliko je vremena prošlo ali opet izgore celi za tačno sat vremena!
Zadatak je da pomoću ta dva kanapa i upaljača, bez pomoći sprava za merenje vremena, odredite tačno 45 minuta!
Da vas vidim...  [ Nedeljko @ 24.01.2009. 17:48 ] @
Jedan upališ sa oba kraja a drugi sa jednog. Kada izgori drugi, onda prvi upališ i sa drugog kraja.
[ ptak 13. @ 24.01.2009. 19:33 ] @
Citat: Nedeljko: Jedan upališ sa oba kraja a drugi sa jednog. Kada izgori drugi, onda prvi upališ i sa drugog kraja.
Da to je tacno resenje, evo novog zadatka:
Citat:
U sobi bez prozora su tri jednake sijalice.
Izvan sobe su tri prekidaca, svaki povezan za jednu od sijalica.
Zadatak je odrediti koji prekidac je povezan za koju sijalicu.
Sme se samo jednom uci u sobu.
[ Zoran Milovanovic @ 24.01.2009. 19:45 ] @
Ako su sa uzarenim vlaknom ondah lako.
Ukljucis jednu sijalicu, ostavis prekidac u tom polozaju.
Ukljucis drugu sijalicu, zatim iskljucis istu.
Uletis u sobu i pipnes od ove dve koje su iskljucene koja je toplija i to je to.
Tako znas koja je za koj prekidac privezana.
:)
[ ptak 13. @ 24.01.2009. 20:09 ] @
^Posto brzo resavate ove zadatke sumnjam da ste provalili isti sajt sa resenjima sa kog ja skidam zadatke pa evo neceg drugacijeg 
U sobi 4*4 m se nalazi jedan mrtav covek. Ekipa policije je upala u sobu i videla da u sobi nema ama bas nicega sem jedne kuke koja je fiksirana na plafonu ( nepomicna kuka ) o nju je bio vezan kanap kojim se obesio nesrecni covek. Ispod coveka nalazila se lokva vode.
Pitanje kako se ubio covek (obesio) ? [ Bojan Basic @ 24.01.2009. 20:12 ] @
Stajao je na kocki leda.  [ ptak 13. @ 24.01.2009. 20:22 ] @
Hahaha najaci ste :) pogledaj PP !
Ajde jos malo....
Evo jedna pa ako pogodite, svaka čast.
Trenutno ga nemaš i ne treba ti. Ali, ako ga ikad budeš trebao i ne budeš ga imao, više ti nikad neće trebati.
I šta je to?
[ Bojan Basic @ 24.01.2009. 20:28 ] @
Padobran.  [ ptak 13. @ 24.01.2009. 20:36 ] @
hehe, takodje tacno....
evo jos jednog....
Jedan spijun treba da udje u tvrdjavu. Postoji samo jedan ulaz, ali tamo strazari kontrolisu svaku osobu koju ulazi. spijun se priblizi malo i gleda kako ljudi ulaze.
prvo dolazi jedan seljak. Strazar ga pita "16, koji je tvoj odgovor?" on odgovori 8 i puste ga da udje. zatim nailazi jedna djevojka, strazar kaze "10, koji je tvoj odgovor?" ona odgovori 5 i nju puste. poslije dolazi jedan svestenik. strazar mu kaze "22, koji je tvoj odgovor?", on kaze 11 i puste ga da udje.
zatim nas spijun pomisli da je skuzio i stane ispred ulaza. strazar ga pita "20, koji je tvoj odgovor?", spijun odgovori 10. zatim ga strazari uhapse i ubiju ga.
sta je spijun uradio pogresno? koji bi bio tacan odgovor? [ X Files @ 24.01.2009. 20:58 ] @
int odgovor( char* izgovoren_broj ) { return ( strlen( izgovoren_broj ) ); }
Priznajem, ne bih nikad resio... Izgooglao sam ;)
[ ptak 13. @ 24.01.2009. 22:53 ] @
he he i ja ne bi skotao nikad....mozda nekad ali kasno :) inace za one koji ne razumeju broj slova koje nosi u svom imenu cifra koju izgovara strazar je kljuc, ili lozinka za ulazak
Mrzi me vise....sutra cu naci neki....
Poz
[Ovu poruku je menjao ptak 13. dana 25.01.2009. u 00:16 GMT+1]
[ Bojan Basic @ 24.01.2009. 23:10 ] @
Citat: ptak 13.:
inace za one koji ne razumeju broj slova koje nosi u svom imenu cifra koju izgovara strazar treba podeliti sa 2 i reci broj koji je kljuc....
Ne, ne treba ništa deliti, treba samo videti od koliko se slova sastoji broj koji stražar izgovara. [ ptak 13. @ 24.01.2009. 23:16 ] @
Da da da, u pravu si, editovo sam :) Izvinjavam se svima na gresci, hvala Bojane ! ! !
[ ptak 13. @ 24.01.2009. 23:20 ] @
Ajde ovaj
U bazenu ima 25 gladnih stuka. Da bi stuke bile site moraju da smazu druge tri stuke (nije bitno gladne ili site, sve imaju jednaku kalorijsku vrednost ). Koliko najvise sitih stuka moze da ostane u bazenu?
[ galet@world @ 25.01.2009. 00:11 ] @
4 = greška
[Ovu poruku je menjao galet@world dana 25.01.2009. u 09:02 GMT+1]
[ WOW @ 25.01.2009. 03:45 ] @
Citat: ptak 13.:U bazenu ima 25 gladnih stuka. Da bi stuke bile site moraju da smazu druge tri stuke (nije bitno gladne ili site, sve imaju jednaku kalorijsku vrednost ). Koliko najvise sitih stuka moze da ostane u bazenu? Zive ili mogu da budu u stomaku druge stuke? [ galet@world @ 25.01.2009. 09:34 ] @
Evo neke računice za 6
25 = 4 + 4 + 4 + 4 + 4 + 5 ako opet nisam pogrešio, a valjda nisam ovaj put
jedna štuka je pojela dve gladne i jednu koja je već pojela jednu tako da u njoj ima 4 štuke, a s njom ih je ukupno 5
[Ovu poruku je menjao galet@world dana 25.01.2009. u 10:45 GMT+1]
[ ptak 13. @ 25.01.2009. 13:06 ] @
Fora je u tome sto ni ja nemam konkretno resenje zadatka....necu jos da pisem moje resenje. Ali ako sam dobro shvatio svaka gladna jede 3 stuke da bi bila sita.....a gladnih ne bi trebalo da ostane....kao neko misli drugacije neka kaze....?!
Po mom proracunu imam 4 site stuke.....i nijednu gladnu.
Pitanje je da li sme da ostane gladna, ako sme onda imam 6 sitih i jednu gladnu, ali nelogicnojeda ostane jedna gladna.
Mislim da je ovo resenje. [ galet@world @ 25.01.2009. 14:40 ] @
Ja izgleda nisam bio jasan
Svaku situ štuku računaj kao 4 - to su 3 u njoj i ona.
5 sitih štuka je 5 puta 4 jednako 20 i ostane još 5 gladnih
Ako jedna od tih 5 pojede 3 štuke onda ostane jedna gladna
a gladna može da jede site kao što si rekao pa bi pojela 3 site i ostalo di dakle 4 site,
ali ...
pitanje je bilo koliko "najviše" sitih štuka ostane u bazenu,
zato kad ostane 5 gladnih neka mora pojesti neku gladnu i sad opet imaš 4 gladne od
kojih jedna gladna pojede ostale tri od kojih je jedna "polusita" i samo tako može biti u
bazenu najviše sitih.
Prema zadatku gladnih ne sme biti jer mogu da jedu site.
Prema tome može biti šest sitih, a po tvom rešenju jedna se zaista prežderala.
[ WOW @ 25.01.2009. 16:13 ] @
6 stuka pojede po 3 gladne (6*4 = 24)
Ostaje jedna gladna... Nju pojede neka vec sita (onako na gladne oci :P) i ostaje 6 sitih u bazenu...
[ Bojan Basic @ 25.01.2009. 16:24 ] @
Citat: WOW:
Ostaje jedna gladna... Nju pojede neka vec sita (onako na gladne oci :P) i ostaje 6 sitih u bazenu...
Ne, ovako će ta gladna pojesti tri site, i ostaće svega četiri u bazenu.
Međutim, moguće je da ostane šest sitih štuka na sledeći način (to galet@world bezuspešno pokušava da objasni, nadam se da ću ja imati više sreće  ). Jedna štuka, nazovimo je Milojka, pojede neku drugu (ali samo jednu). Tako ostaju 24 štuke. Šest od njih, među kojima nije Milojka, sada pojede preostalih 18 (u ovoj grupi je i Milojka), svaka po tri. [ ptak 13. @ 25.01.2009. 16:26 ] @
Da, da, da, sad sam probao i dobio resenje da je najveci broj stuka 6 (sitih naravno )
aj sad da vas vidim
Janin tata ima 5 cerki
Nono
Nunu
Nini
Nana
Kako se zove peta cerka?
[ Zoran Milovanovic @ 25.01.2009. 16:33 ] @
Nene?
[ Zoran Milovanovic @ 25.01.2009. 16:34 ] @
Jana naravno :)
[ ptak 13. @ 25.01.2009. 17:20 ] @
hehehe upecao si se :) da Jana se zvala ! ! !
LJudi za ovu seriju zadataka nemam resenje, i ja lupam glavu sa njima....ajde da vidim vas.
Zarko ima 4 godine i stanuje na 18-om spratu. Kada sam ulazi u lift on se vozi samo do 16-tog sprata, a dalje nastavlja put pesice. Zasto ?
[ Zoran Milovanovic @ 25.01.2009. 17:22 ] @
zato sto ima 4 godine i ne moze da dohvati taster 18. :)
[ ptak 13. @ 25.01.2009. 17:36 ] @
Ne verujem da je to resenje, ja trazim vezu izmedju 4x4=16 ali nisam siguran ! ! ! [ Zoran Milovanovic @ 25.01.2009. 17:42 ] @
Nema tu nikakve veze, resenje je ovo. Videcemo sta ce drugi da kazu.
[ ptak 13. @ 25.01.2009. 17:47 ] @
Mozda si u pravu....znaci cekamo da vidimo jos neko resenje.
Evo jos jednog ! ! !
Taksista je skrenuo u ulicu u kojoj je zabranjeno kretanje svim motornim vozilima. Kada je prosao pored saobracajnog milicionera ovaj ga srdacno pozdravi. Zasto milicioner nije kaznio taksistu ?
Ovaj sam resio, resenje nije da su pijani, da su braca i sl  [ Zoran Milovanovic @ 25.01.2009. 17:54 ] @
Taksista je zanimanje, ne mora da znaci da je isao kolima? Mozda je isao pesaka? A usput poznavao pandura?
[ WOW @ 26.01.2009. 00:32 ] @
1) Par konja je presao 30km. Koliko je presao svaki od konja?
2) Na Novogodisnjoj jelki je gorelo 9 sveca (vostanih), ali su 4 svece ugasene. Koliko je sveca ostalo sutradan?
3) Jedno jaje se kuva 4 minuta. Koliko minuta se kuvaju 4 jajeta?
4) Ako u Beogradu u ponoc pada kisa moze li se za 48 casova ocekivati suncano vreme?
5) Zasto berberin koji je iz Valjeva vise voli da podsisa dva Beogradjanina nego jednog Valjevca?
:P
[ Zoran Milovanovic @ 26.01.2009. 01:06 ] @
Ovako pripit vidim jasno odgovor na sledeca pitanja:
1. 30km
3. 4min
4. Ne, bice ponoc.
xP
Nemam pojma za ova 2, odo da spawam :)
[ Daniel011 @ 26.01.2009. 09:20 ] @
2) Pod pretpostavkom da su se sveće koje su gorele do sutradan istopile, ostale su 4 sveće.
5) Ako je berberin iz Valjeva a živi i radi u Beogradu, logično je da će više voleti da podšiša dva Beograđanina nego da putuje do Valjeva da bi podšišao jednog Valjevca.
[ Zoran Milovanovic @ 26.01.2009. 09:55 ] @
Meni je sinoc padalo isto napamet, ali nisam mogao bas bistro da razmisljam, pa nisam hteo ni da pisem. Cekacemo da dodje master, da vidimo jesmo li tacno odg.
Inace, evo jutros sveze glave razmisljam za taksistu pa mi sinulo, da nije taksista "taksirao" biciklom, kao u kini oni? :D
[ WOW @ 26.01.2009. 17:03 ] @
A pa ja nemam odgovore na ova pitanja a uzeo sam ih iz neke zbirke za 4 razred xD
Mislim da je stvar sa poslednjim da bi berberin radije osisao 2 osobe nego jednu bez obzira iz kog su grada...
A taksista je isao peske... Tog zadatka se secam jos od kada sam bio mali
[ ptak 13. @ 28.01.2009. 23:42 ] @
Evo jedan zadatak za mozganje.
Jovan, Mitar i Bora rade u tri razlicita mesta. Svaki u po jednom, Pirotu, Nisu i Kikindi i to u prodavnicama obuce, gvozdja i alkohola. Jovan ne radi u Pirotu, Mitar ne radi u Nisu, Pirocanac ne prodaje alkohol. Nislija prodaje obucu, Mitar ne prodaje gvozdje. U kojoj prodavnici i u kom gradu rade trgovci ?
Ajde da vas vidim, i dajte vi neki zadatak....?!  [ sanja2010 @ 28.01.2009. 23:53 ] @
Mitar ne prodaje gvozdje, a ni obucu jer nije Nishlija (Nish ftw! :D), znaci Mitar prodaje alkohol. Nije Pirocanac, a ni Nishlija, pa je Kikindjanin. Jovan nije Pirocanac pa mu ostaje Nish i obuca, a Bori Pirot i gvozdje :)
Volela sam ove zadatke kad sam bila mala... :)
[ ptak 13. @ 29.01.2009. 13:01 ] @
Bravo Sanja....sto volim kad vidim da ima cura na ESu....hehehehe
evo novog zadatka.
Koliko najvise kvadrata mozete nacrtati a dasvaki od njih ima po 2 zajednicka temena....nadam se da sam lepo objasnio ?
[ zzzz @ 29.01.2009. 18:44 ] @
Citat: ptak 13.: ....nadam se da sam lepo objasnio ?
Nisi.
Jer mogao bi povezati u krug mnogo kvadrata koji se drže za po jedno tjeme. [ Zoran Milovanovic @ 29.01.2009. 19:35 ] @
Citat: ptak 13.: Koliko najvise kvadrata mozete nacrtati a dasvaki od njih ima po 2 zajednicka temena....nadam se da sam lepo objasnio ?
@zzzz
Mislim da ti ipak nisi dobro razumeo. [ Tea94 @ 29.01.2009. 19:47 ] @
evo i ja da se prikljucim... da nije mozda 5?
[ ptak 13. @ 29.01.2009. 22:10 ] @
Citat: zzzz: Nisi.
Jer mogao bi povezati u krug mnogo kvadrata koji se drže za po jedno tjeme.
Brate dva temena....ne jedno....
Citat: Tea94: evo i ja da se prikljucim... da nije mozda 5?
U jbt daj sliku da vidim, ja sam uspeo 3 naci ! ! ! :))))))skiciraj u paint ili nesto sl. [ Zoran Milovanovic @ 29.01.2009. 22:27 ] @
ptak. 13 daj tvoju skicu da vidim da li sam dobro razumeo, jer ja sam nasao 4 kvadrata koji su u krug poredjani, a samim tim u sredini se dobija izgled jos jednog, ali njega ne mogu da ubrijim jer on ima 4 zajednicka temena... :)
[ Bojan Basic @ 29.01.2009. 22:31 ] @
Ali onda nikoja dva nemaju dva zajednička temena, samo po jedno.  [ Zoran Milovanovic @ 29.01.2009. 22:43 ] @
lol, koja ispala... pa kazem ja da je meni nesto cudno tu :)
bruka :)
[ Tea94 @ 29.01.2009. 22:43 ] @
ovako sam ja to zamislila... stavis 1 kvadrat u sredinu, i 4 oko njega... i onda svi oni imaju po 2 zajednicka temena sa ovim u sredini...
[ ptak 13. @ 29.01.2009. 22:43 ] @
Evo ja sam uradio ovako, ne znam da li je tacno, ali nigde se ne spominje da moraju biti jednaki ?!
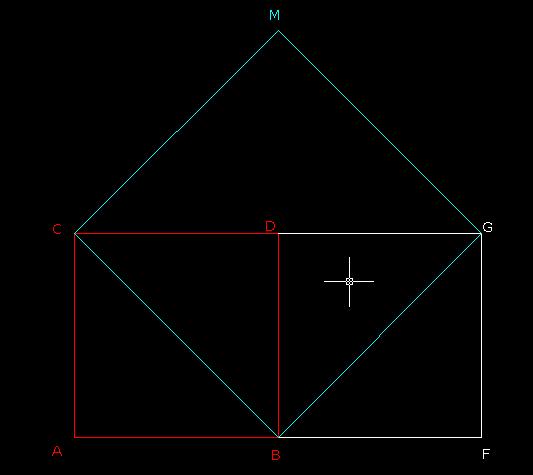
Aj da cujem misljenja.....
I u AutoCAd sam morao da crtam  [ Tea94 @ 29.01.2009. 23:03 ] @
sta reci... bravo...
ae sad nesto novo...
Ovu je zagonetku Albert Einstein sastavio u 20. stoljeću. Tvrdio je da je moze rijesiti samo 2% svjetske populacije.
Zadatak s kojim se morate suočiti:
1. Postoji pet kuća i svaka je različite boje.
2. U svakoj kući živi po jedna osoba različite nacionalnosti.
3. Stanar svake kuće ima svoje omiljeno piće.
4. Stanar svake kuće ima omiljenu marku cigareta.
5. Stanar svake kuće ima neku kućnu životinju.
Pitanje: Čiji je zec ?
Detalji:
Britanac živi u crvenoj kući.
Šveđanin ima psa.
Danac voli piti čaj.
Zelena kuća lijevo je od bijele.
Vlasnik zelene kuće pije kavu.
Pušač Pall Mall-a drži pticu.
Čovjek koji živi u srednjoj kući pije mlijeko.
Vlasnik žute kuće puši Dunhill.
Norvežanin stanuje u prvoj kući.
Pušač Marlbora stanuje pokraj onoga koji ima mačku.
Čovjek koji ima konja stanuje pokraj onoga koji puši Dunhill.
Čovjek koji puši Winston rado pije pivo.
Norvežanin stanuje pokraj plave kuće.
Nijemac puši Rothmanns.
Čovjek koji puši Marlboro ima susjeda koji pije vodu.
[ ptak 13. @ 29.01.2009. 23:11 ] @
Da ovo je Anstajnov test intalegencije.....radio sam ga pre oko godinu dana i resio za sat-dva vremena....tacno je da je receno da samo 2% ljudi moze da ga resi, ali ja u to sumnjam, evo okacicu sad resenje, samo da ga iskopam. Radio sam to davno postoji program napisan u Delphy-u za to i evo ako nadjem resenje po silnim resenjima u paprnom obliku skeniram i kacim....dok ne nadjem mucite se malo....nije bas lako ! ! !
Ajde necu jso da kacim resenje....da vidim hoce li iko da resi 
heheh, nasao sam resenj....poslacu ti na PP, a ovde necu jos da kacim
Srecno svima ! ! ! [ Tea94 @ 29.01.2009. 23:14 ] @
pise 2%, ali ako sam JA uspela da resim, moze bilo ko  [ zzzz @ 29.01.2009. 23:48 ] @
Da nije možda: svaki sa svakim ima po dva zaj.tejmena, a neko tjeme može biti zajedničko
za više kvadrata.Kvadrati ne moraju biti jednaki.Ili da uvedemo pravilo umjetničke slobode.
 [ ptak 13. @ 29.01.2009. 23:55 ] @
Citat: zzzz: Da nije možda: svaki sa svakim ima po dva zaj.tejmena, a neko tjeme može biti zajedničko
za više kvadrata.Kvadrati ne moraju biti jednaki.Ili da uvedemo pravilo umjetničke slobode.

Jao, jao, jao.....
Pazi svaki kvadrat mora da sa drugim ima 2 zajednicka temena.....pa da ti objasnim....
kazes "mnogo" ok koje zajednicko teme imaju prvi dole i treci ? nijedno
"dva" OK, ali moze i 3 kao kod mene.
"pet" Koje zajednicko teme imaju zeleni i plavi kvadrat ? znaci ne moze......to resenje ne moze....
"dva" Ok moze i 3
"Mnogo" pa sta vise puta po dva, to nije resenje.....
Znaci ima dva dobra resenja ali moze i vise.....sto sam dokazao gore.
A ovo ostalo nema veze sa zadatkom.....
Znaci prvi kvadrat mora imati dva temena zaednicka sa drugim, onda drugi sa trecim, treci sa prvim....kontas ?????
[ mjux @ 30.01.2009. 00:27 ] @
nemac ima zeca
[ Daniel011 @ 30.01.2009. 17:57 ] @
O Ajnštajnovom zadatku je već bilo reči u ovoj temi.
Ja mislim da jeste dobro razumeo, jer je zadatak prvobitno bio tako neprecizno formulisan da je mogao da se tumači i na taj način, tj. da svaki kvadrat ima tačno dva temena koja su zajednička sa nekima od ostalih kvadrata. Tek naknadno je objašnjeno da se traži da svaki kvadrat treba da sa svakim kvadratom ima dva zajednička temena. [ Zoran Milovanovic @ 30.01.2009. 19:26 ] @
Ok, never mind...
http://www.elitesecurity.org/t28555-20#2183483 <----click
pored boldovanog teksta dve reci u levo pise "dasvaki od", ja stvarno ne znam kako ces ti to da tumacis. Ali sem sto fali razmak, sve ostalo je jasno! [ ptak 13. @ 30.01.2009. 20:10 ] @
Ljudi da li sam ja nepismen ili sta je u pitanju ?
Nisam editovao post, zadatak je dovoljno jasan i ja sam da omoguce resenje, mozda postoji jos koje....ne znam ?!
[ Daniel011 @ 30.01.2009. 21:19 ] @
Citirao bih još jednom kako je glasila prvobitna postavka zadatka:
Citat: Koliko najvise kvadrata mozete nacrtati a dasvaki od njih ima po 2 zajednicka temena....nadam se da sam lepo objasnio ?
Izraz zajednički je sâm po sebi nedorečen, ukoliko se ne odredi sa čime je to na šta se misli zajedničko. Ovako kako je zadatak (nejasno) postavljen, jedno od rešenja koje je prikazao zzzz, a koje sam ilustrovao na sledećoj slici
[att_img]
je sasvim validno.
Na ovoj slici, svaki kvadrat ima tačno dva temena koja su zajednička. Zajednička su sa nekima od preostalih kvadrata na slici. Primera radi, kod kvadrata CEFG to su temena C i G:
C je zajedničko sa kvadratom ABCD, a G je zajedničko sa kvadratom GHIJ.
Ne želim da sve ovo izgleda kao teranje maka na konac, ovo je dobronamerna primedba, kako bi budući zanimljivi zadaci bili što preciznije formulisani. [ galet@world @ 31.01.2009. 10:28 ] @
Evo precizne formulacije jednog zadatka:
Preseci pravougaonik 4 x 9 na dva jednaka dela tako da od tih delova možeš sastaviti kvadrat.
[ Daniel011 @ 31.01.2009. 12:14 ] @
S obzirom da nigde nije rečeno da se pravougaonik mora preseći po pravoj liniji  , evo mog rešenja:
[att_img] [ ptak 13. @ 31.01.2009. 12:26 ] @
Bravo Daniel011....pretekao si me :D
[ galet@world @ 31.01.2009. 18:18 ] @
Ajd' sad 16 x 9
[ ptak 13. @ 31.01.2009. 19:39 ] @
Evo resenja

Nadam se da nisam pogresio u montazi 
P.S. Kod mene se nesto ne vidi slika pa evo download
http://www.sendspace.com/file/ekgus3[ ptak 13. @ 31.01.2009. 20:00 ] @
evo jedan za razmisljanje.
Podelite casovnik dvema pravama tako da sume brojeva u podeljenim delovima budu jednake.
[ Tea94 @ 31.01.2009. 20:10 ] @
ne znam da stavim sliku, pa cu samo da objasnim:
linija prolazi izmedju 9 i 10, i izmedju 3 i 4.
tako da na jednoj strani imamo 10+11+12+1+2+3 = 39
a na drugoj 4+5+6+7+8+9=39
[ Daniel011 @ 31.01.2009. 20:27 ] @
Prema zadatku, časovnik je trebalo podelliti dvema pravama:
[att_img]
[ Tea94 @ 31.01.2009. 20:31 ] @
znaci da se vratim kad naucim da citam?  [ galet@world @ 01.02.2009. 13:55 ] @
Koliko je TAČNO sati kad mala kazaljka stoji između 10 i 11 a velika između 4 i 5 po pravoj liniji?
[ ptak 13. @ 01.02.2009. 14:02 ] @
Citat: galet@world: Koliko je TAČNO sati kad mala kazaljka stoji između 10 i 11 a velika između 4 i 5 po pravoj liniji?
PA ne mogu da stoje po pravoj liniji :) ?! Bar kod mene ! ! ! [ Tea94 @ 01.02.2009. 14:21 ] @
pa ne bi moglo po pravoj liniji, ali bilo bi 10:23 
a ko je spominjao velike i male kazaljke? pisalo je PRAVA a ne KAZALJKA [ Daniel011 @ 01.02.2009. 14:27 ] @
10 h21 m49 s
Postupak:
Velika kazaljka, računajući od broja 12, u CW smeru, zaklapa neki ugao V. Mala kazaljka po istom pravilu zaklapa neki ugao M. Traži se da bude M-V=180º.
Kazaljke će biti u pravcu u 10 sati i x minuta:
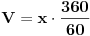
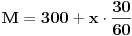
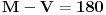
Odavde dobijamo 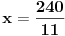 , što kad se pretvori u minute i sekunde, bude kao što sam prethodno napisao. [ ptak 13. @ 01.02.2009. 14:59 ] @
A zasto ja ovo ne kontam :)
Sta je smer CW ? pojasni mi to
Onda zaklapa ugao V u odnosu na koje brojeve ....nije mi bas jasna ova tvoja teorema :) ! ! !
[ Tea94 @ 01.02.2009. 15:10 ] @
kolko se ja secam, ugao CW je na dole a CCW na gore...
[ Daniel011 @ 01.02.2009. 15:15 ] @
CW i CCW su ti međunarodne skraćenice, CW znači clockwise, tj. u smeru kazaljke sata, a CCW znači counterclockwise, tj. u smeru suprotnom od kazaljke sata. Ovde imaš o tome detaljnije.
Sa V sam obeležio ugao za koji je velika kazaljka pomerena u odnosu na broj 12 na satu, gledano u smeru njenog kretanja, tj. u CW smeru. Npr. kad je velika kazaljka na broju 1, ugao V je 30º, kad je na broju 3, taj ugao je 90º...
Nadam se da sam pojasnio.  [ ptak 13. @ 01.02.2009. 15:34 ] @
Jasnije mi je THX 
Sad cu da iskopam neki zadatak ! [ galet@world @ 01.02.2009. 16:36 ] @
Daniele 011 tražio sam 100 % (stoposto) tačno vreme u satima
[ Daniel011 @ 01.02.2009. 17:15 ] @
Pitanje je glasilo "Koliko je TAČNO sati...", ali u redu, ako želiš rezultat u satima kao mernim jedinicama, to bi bilo:
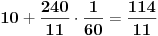
Ovako, u obliku razlomka, rezultat je sa 100%-nom tačnošću. [ zzzz @ 01.02.2009. 17:38 ] @
Neznamo jer imamo 2 rješenja.
X(1)=114/11 sati
X(2)=246/11 sati
[ galet@world @ 01.02.2009. 18:05 ] @
@Daniel011 i zzzz
Odgovor je: deset sati i četiri jedanaestine sata. Milane - odakle ti dva rešenja?
[ Daniel011 @ 01.02.2009. 18:17 ] @
Citat: galet@world: @Daniel011 i zzzz
Odgovor je: deset sati i četiri jedanaestine sata.
Da, a to je isto što i 114/11 sata, koliko smo zzzz i ja i napisali.
Milan je pretpostavio (po meni, sasvim opravdano) da se vreme može računati i u 24hrs formatu, pa se samim tim pojavljuje još jedno rešenje - 10 sati i 4/11 sata uveče, tj. 22 sata i 4/11 sata. [ galet@world @ 01.02.2009. 21:41 ] @
Odmah mi je bilo jasno šta je Milan pretpostavio - ja ne znam kako je kod vas ali kod nas je noću mrak!!!
(i onda "znamo koliko je sati" - ne zamerite na šali)
[ Tea94 @ 03.02.2009. 00:11 ] @
ajmo nesto novo:
U jednom autobusu ima 7 devojaka.
Svaka devojka ima 7 torbi.
U svakoj torbi ima 7 velikih macaka.
Svaka velika macka ima 7 malih macica.
Svaka macka ima 4 noge.
Pitanje: Koliko nogu je prisutno u autobusu?
[ mjux @ 03.02.2009. 03:08 ] @
krenimo od nazad :)
jedno malo mace ima 4 noge kao i veliko.. tako da se u jednoj torbi nalazi 8 macaka :).. sto mu dodje noga 8x4=32
imamo 7 torbi u autobusu.. tako da je ukupno nogu od macaka u busu 7x32=224
na taj broj dodajemo noge od 7 devojaka :).... sto je 224+(7*2)=328
i na kraju .. neko mora da vozi taj bus.. tako da dodajemo 2 noge za vozaca ili 4 noge za vozaca i konduktera(ako taj postoji)
sto mu dodje ili 330 ili 332
ja mislim da je to caka sa tim vozacem ali moze biti i druga stvar.. npr.. nigde se ne kaze da su macici u busu nego da
svaka macka ima 7 macica koji mogu a i ne moraju da budu u busu, isto vazi i za torbe, koje isto ne moraju biti u busu..
[ Tea94 @ 03.02.2009. 08:55 ] @
nije tacno, procitaj bolje zadatak...
ima 7 devojaka u busu. SVAKA ima 7 torbi. u SVAKOJ se nalazi 7 macaka. u SVAKOJ macki ima 7 macicia.
a kondukter i vozac se ne racunaju.
na kraju se dobije neverovatno veliki broj...
[ noviKorisnik @ 03.02.2009. 12:25 ] @
7 * (devojka + 7 * torba)
= 7 * (2 * noga + 7 * (7 * (mačka + 7 * mače)))
= 7 * (2 * noga + 7 * (7 * (4 * noga + 7 * 4 * noga)))
= 7 * (2 + 7 * 7 * (1 + 7) * 4) * noga
to je oko 10990 nogu
[ bata kg @ 03.02.2009. 16:34 ] @
Za mene jedan od najlepsih:
Iz tri merenja na terazijama odrediti, od 12 kuglica, koja je laksa ili teza?
[ Tea94 @ 03.02.2009. 18:25 ] @
to je lako...
Kuglice se podele na tri grupe, ali da te grupe ne budu jednake:
2x3 kuglice
2x2 kuglice
2x1 kuglica
Prvo se meri 6 kuglica, na jednoj strani 3, na drugoj strani 3:
ako su 2x3 kuglice iste tezine, mere se 2x2 kuglice
ako su 2x2 kuglice iste tezine, merimo 2x1 kuglica
ali ako 2x3 kuglice nisu iste tezine, onda pravimo dve grupe: 2x2, 2x1, pa sve isto kao u prethodnom slucaju.
[ zzzz @ 03.02.2009. 18:38 ] @
Zapravo imamo 11 jednakih kuglica i jednu različitu.Ali ne znamo da li je L ili T.
Mislim da je ovo već bilo riješeno prije 5-6 godina.
[ Tea94 @ 03.02.2009. 19:00 ] @
ima vise verzija... to sa 12 i 11 kuglica. i ono sa 5 zlatnika... mislim da je cak i u ovoj temi bilo...
[ mitrovicva @ 03.02.2009. 22:49 ] @
imate 10 cupova i u njima su zlatnici tezine svaki po 1 gram, ali u jednom su tezine pola grama.Kako samo jednim merenjem na terazijama odrediti u kom cupu su laksi zlatnici
[ mitrovicva @ 03.02.2009. 23:00 ] @
imate tri crna i dva bela sesira i izmesaju se. Postave se tri coveka u red i stavi se svakome na glavu po jedan sesir ali tako da ne vidi koje je boje obod svog sesira.Poslednji u koloni vidi ona dva ispred i na pitanje loje je boje njegov sesir , odgovara da ne zna.Covek u sredini vidi koje je boje sesir ispred njega i na pitanje koje je boje njegov sesir takodje odgovara da ne moze znati, i na kraju prvi covek koji ne vidi ni jedan sesir na pitanje koje je boje njegov odgovara tacno.
[ Daniel011 @ 03.02.2009. 23:39 ] @
Da li u zadatku sa ćupovima imamo na raspolaganju terazije sa svim potrebnim vrednostima tegova?
Ako je to slučaj, onda iz prvog ćupa uzmemo jedan zlatnik, iz drugog dva, iz trećeg tri, ..., iz desetog deset zlatnika, stavimo ih sve na jedan tas i izmerimo koliko zajedno imaju grama.
Zadatak sa šeširima:
Mada nije eksplicitno rečeno, pretpostavljam da sva tri čoveka znaju da su "u igri" ukupno tri crna i dva bela šešira.
Da je poslednji u koloni video ispred sebe dva bela šešira, onda bi znao da njegov šešir mora biti crn. Pošto je on odgovorio da ne zna koje je boje njegov šešir, to onda znači da ona dva šešira ispred njega nisu oba bela, odnosno da je bar jedan crn. Znajući ovo, čovek u sredini bi, da je ispred sebe video beo šešir, znao da njegov šešir mora biti crn. Međutim, s obzirom da je i njegov odgovor bio da ne zna koje je boje njegov šešir, ostaje da šešir prvog čoveka u koloni mora biti crn, što je on upravo i zaključio.
[ Tea94 @ 04.02.2009. 11:41 ] @
Na porodicnom skupu bili su 1 deda, 1 baba, 2 oca, 2 majke, 4 dece, 3 unuka, 1 brat, 2 sestre, 2 sina, 2 cerke, 1 svekar, 1 svekrva i 1 snaja. Koliko je pojedinaca bilo prisutno? (nabrojati)
[ galet@world @ 04.02.2009. 11:41 ] @
Evo jednog zadatka sa šibicama - malo podužeg, ali interesantnog. Šibice su postavljene u četiri reda.
U prvom redu je jedna šibica, u drugom tri, u trećem pet i u četvrtom sedam šibica. Ovo je igra za
dva takmičara. Pravilo igre je sledeće: Tamičari naizmenično uzimaju šibice iz postavljenih redova
po pravilu da onaj koji je na redu može uzimati šibice iz bilo kog reda, ali samo jednog reda i bilo koliko
t.j. mora uzeti bar jednu ili čak i sve iz tog reda, zatim vuče drugi takmičar i t. d. sve dok ne uzmu
sve šibice - onaj koji vuče zadnji je izgubio partiju
Ako, na primer, jedan takmičar ostavi drugom takmičaru poziciju da se u dva reda nalaze po dve šibice
onda drugi takmičar obavezno gubi, jer ako drugi takmičar koji je na redu za vučenje i izvuče iz bilo
kog reda obe šibice, onda će prvi takmičar iz preostalog reda izvući samo jednu tako da drugi takmičar
gubi jer mora uzeti tu jednu. Ako drugi takmičar, međutim, izvuče iz nekog od ta dva reda samo jednu
šibicu, onda će prvi takmičar u zeti ceo red u kom su dve šibice tako da drugom takmičaru opet ostane
jedna i poslednja pa prema tome opet gubi.
Postavlja se pitanje koje sve pozicije su dobitne za igrača koji ih ostavlja svom protivniku.
Ne znam da li sam bio dovoljno jasan, ali ako nisam pitajte.
[ galet@world @ 04.02.2009. 11:54 ] @
Sedmoro
baba deda
sin snaja
dve ćerke i sin
Ali bilo je njih još: dve supuge i dva supruga (ali oni nisu rod)
[ noviKorisnik @ 04.02.2009. 14:58 ] @
Citat: galet@world: Evo jednog zadatka sa šibicama - malo podužeg, ali interesantnog. Šibice su postavljene u četiri reda.
U prvom redu je jedna šibica, u drugom tri, u trećem pet i u četvrtom sedam šibica. Ovo je igra za
dva takmičara. Pravilo igre je sledeće: Tamičari naizmenično uzimaju šibice iz postavljenih redova
po pravilu da onaj koji je na redu može uzimati šibice iz bilo kog reda, ali samo jednog reda i bilo koliko
t.j. mora uzeti bar jednu ili čak i sve iz tog reda, zatim vuče drugi takmičar i t. d. sve dok ne uzmu
sve šibice - onaj koji vuče zadnji je izgubio partiju
Ako, na primer, jedan takmičar ostavi drugom takmičaru poziciju da se u dva reda nalaze po dve šibice
onda drugi takmičar obavezno gubi, jer ako drugi takmičar koji je na redu za vučenje i izvuče iz bilo
kog reda obe šibice, onda će prvi takmičar iz preostalog reda izvući samo jednu tako da drugi takmičar
gubi jer mora uzeti tu jednu. Ako drugi takmičar, međutim, izvuče iz nekog od ta dva reda samo jednu
šibicu, onda će prvi takmičar u zeti ceo red u kom su dve šibice tako da drugom takmičaru opet ostane
jedna i poslednja pa prema tome opet gubi.
Postavlja se pitanje koje sve pozicije su dobitne za igrača koji ih ostavlja svom protivniku.
Ne znam da li sam bio dovoljno jasan, ali ako nisam pitajte. [ Daniel011 @ 04.02.2009. 15:09 ] @
Citat: bata kg: Za mene jedan od najlepsih:
Iz tri merenja na terazijama odrediti, od 12 kuglica, koja je laksa ili teza?
Bio je sličan zadatak na ovoj temi i dato je rešenje za različite verzije tog zadatka, koje uključuje i ovu verziju sa 12 kuglica.
@Tea94 Tvoje rešenje bi bilo sasvim korektno, kada bismo znali da li je različita kuglica lakša ili teža. [ zzzz @ 04.02.2009. 23:27 ] @
Citat: galet@world: Evo jednog zadatka sa šibicama - malo podužeg, ali interesantnog. .
Predlažem:
-Postavi ti nešto više redova (bar 4) sa po nešto više šibica u svakom redu po želji.
Naprimjer:123,77,69,41,19,7,6,3,2,1(imamo 10 redova)
-Ja ću onda predložiti ko prvi vuče.
-Ti onda odredi da li: a) gubi onaj koji zadnji vuče a dobija onaj koji je predzadnji
vukao ili b)pobjeđuje onaj koji zadnji vuče a gubi onaj koji predzadnji vuče.
Otpočnemo li igru zna se:Ti ćeš izgubiti i to svaki puta u "n" pokušaja.Ako ne vjeruješ a ti probaj. [ galet@world @ 05.02.2009. 16:36 ] @
A kako bi igrali - od poruke do poruke?
Ovoga se sećam odavno, ali nisam znao da je to neko matematički rešio i u stvari pokvario igru. Tako će možda biti i sa šahom.
Igrali smo pa ko pobedi, ali ponešto smo i zaključivali. Matematičko rečenje mi nije poznato niti
nameravam da ga upoznajem - u svakom slučaju postalo je neinteresantno.
[Ovu poruku je menjao galet@world dana 05.02.2009. u 18:18 GMT+1]
[Ovu poruku je menjao galet@world dana 05.02.2009. u 18:22 GMT+1]
[ zzzz @ 05.02.2009. 23:37 ] @
Dane kaže: Matematičko resenje mi nije poznato niti
nameravam da ga upoznajem - u svakom slučaju postalo je neinteresantno.
-------------
Svi zadaci na ovom forumu su dati bez rješenja.Ako neko nema namjeru tražiti
rješenja zadataka, a niti ga interesuje kako je to neko drugi rješio ili bar kako glasi
rješenje, nije mi jasno šta ga onda interesuje ovdje.
(Bojan i noviKorisnik neka dozvole ostalima da se pozabave rješavanjem bar neko vrijeme.)
[ galet@world @ 06.02.2009. 16:08 ] @
Nije to isto Milane. Drugo je problem kome ne znamo rešenje i čije rešenje zavisi od puta koji kreiraju dva protivnika.
To je igra. Doduše logička, ali interesantna po tome što ni jedan protivnik ne zna uvek rešenje za novonastale uslove
koje mu nameće suparnik. Ko bi igrao šah ako bi se znalo kako onaj ko prvi vuče potez obavezno dobija ili gubi?
Da li je tebi interesantan problem koji si rešio? Bio je dok ga nisi rešio, a posle tražiš drugi. Da li ti je interesantan
problem koji je neko drugi rešio i pokazao ti rešenje? Za mene bi on bio interesantan samo ako ja imam priliku da ga
rešavam
Problem sa šibicama je interesantan po tome što pruža ljudima zadovoljstvo u traženju dobitnih pozicija, ali ako je
neko rešio sve moguće pozicije pomoću nekog algoritma - onda to zadovoljstvo otpada. Gotovo je. Nema više.
[ zzzz @ 07.02.2009. 00:50 ] @
??Problem sa šibicama je interesantan po tome što pruža ljudima zadovoljstvo u traženju dobitnih pozicija, ali ako je
neko rešio sve moguće pozicije pomoću nekog algoritma - onda to zadovoljstvo otpada. Gotovo je. Nema više.
Gotovo sve zadatke koji se ovdje izlažu neko je već ranije riješio.Ali mi neznamo pa
pokušavamo naći rješenje.I to nam je zabava.A onaj ko zna ponešto pomogne ako nam stane mozak.Zašto ti i ostali koji ne znate "algoritam" mislite da nije zadovoljstvo naći opšte rješenje za ovakav zadatak?Daleko je ovo od šaha.Čak je bez smisla praviti
program na računaru za ovakve stvari, iako je neko i to uspješno uradio.Sa malo kombinatorike prosječan čovjek će bez upotrebe olovke
i papira, za pola minuta reći sve o taktici naprimjer u ovakvoj situaciji:
11, 10, 6, 5, 3, 1.(Ko ovdje gubi?)
Sa malo truda prosječan rješavač ovakvih zagonetki će naći pravilo za opštu taktiku.
Ajmo riješite problem, pronađite tu taktiku, a poslije se žalite zbog podvale upravi
vodovoda.
[ bata kg @ 07.02.2009. 21:15 ] @
Najlepsi deo nekog zadatka nije resenje, vec moj"misaoni" put sa svim manjim i vecim skretanjima ka resenju.
Jedan lep problem, natera coveka da razmislja o osobinama samih brojeva.
RE+MI=FA
DO+SI=MI
LA+SI=SOL
[ Daniel011 @ 08.02.2009. 01:09 ] @
Citat: bata kg:
RE+MI=FA
DO+SI=MI
LA+SI=SOL
Ako pretpostavimo da svako slovo predstavlja cifru nekog broja i da sva slova predstavljaju različite cifre, onda se njihove vrednosti mogu izračunati sledećim postupkom:
- Iz DO+SI=MI zaključujemo da O predstavlja cifru 0;
- Iz LA+SI=SOL, imajući u vidu da zbir dva dvocifrena broja ne može biti veći od 198, zaključujemo da S predstavlja cifru 1;
Dati sistem postaje
RE+MI=FA
D0+1I=MI
LA+1I=10L
- Iz LA+1I=10L zaključujemo da L može biti 8 ili 9. U slučaju da je L=8, biće A+I=18, odnosno A=9 i I=9, što je u suprotnosti sa polaznom pretpostavkom da sva slova predstavljaju različite cifre. Znači, preostaje slučaj L=9.
RE+MI=FA
D0+1I=MI
9A+1I=109
- Iz 9A+1I=109 zaključujemo da je A+I=9. S obzirom da A i I ne mogu imati vrednosti 0, 1 i 9 (koje su već pridružene odgovarajućim slovima), moguće su sledeće kombinacije:
(A,I)=(2,7)
(A,I)=(3,6)
(A,I)=(4,5)
(A,I)=(5,4)
(A,I)=(6,3)
(A,I)=(7,2)
Kombinacija (A,I)=(4,5) otpada jer bi tada prva jednačina sistema glasila RE+M5=F4, iz čega sledi da bi moralo biti E=9, a vrednost 9 je već dodeljena slovu L.
Takođe, otpada i kombinacija (A,I)=(5,4), jer bi tada prva jednačina glasila RE+M4=F5, pa bi tada E moralo biti 1, a vrednost 1 je već dodeljena slovu S.
Otpada i kombinacija (A,I)=(6,3) jer bi tada prva jednačina glasila RE+M3=F6, pa bi tada E moralo biti 3, a ta vrednost je (po pretpostavci) već dodeljena slovu I.
Prema tome, ostaju kao moguće kombinacije:
(A,I)=(2,7)
(A,I)=(3,6)
(A,I)=(7,2)
Kombinacija (A,I)=(2,7):
RE+M7=F2 -> R5+M7=F2
D0+17=M7
92+17=109
Preostale cifre su 3,4,6,8. Pošto iz druge jednačine sledi D+1=M, D mora biti 3, a M mora biti 4:
R5+47=F2
30+17=47
92+17=109
Ne postoji način da slovima R i F pridružimo preostale vrednosti 6 i 8, a da prva jednačina bude zadovoljena.
Kombinacija (A,I)=(7,2):
Na sličan način se dokazuje da ni ova kombinacija ne dovodi do rešenja sistema.
Kombinacija (A,I)=(3,6):
RE+M6=F3 -> R7+M6=F3
D0+16=M6
93+16=109
Preostale cifre su 2,4,5,8. Pošto iz druge jednačine sledi D+1=M, D mora biti 4, a M mora biti 5:
R7+56=F3
40+16=56
93+16=109
Preostale cifre 2 i 8 se mogu pridružiti slovima R i F tako da i prva jednačina bude zadovoljena:
27+56=83
40+16=56
93+16=109
Prema tome,
R=2
E=7
M=5
I=6
F=8
A=3
D=4
O=0
S=1
L=9 [ galet@world @ 08.02.2009. 18:00 ] @
To isto:
.............S E N D
......... + M O R E
........———————
..........M O N E Y
[ Daniel011 @ 08.02.2009. 19:20 ] @
S=9
E=5
N=6
D=7
M=1
O=0
R=8
Y=2
odnosno
.............9 5 6 7
......... + 1 0 8 5
........———————
..........1 0 6 5 2
Objavljivanje postupka ću ovaj put prepustiti nekom drugom, da ne bih pokvario zabavu. 
Baš mi se sviđaju ovakvi zadaci.  [ galet@world @ 10.02.2009. 16:52 ] @
Evo jednog baš lepog, on se može rešiti, ali poslati odgovor je vrlo teško
izuzev ako niste posebno nadaren crtač.
[ bata kg @ 10.02.2009. 17:31 ] @
Dok ne nabavim malo cvrsci karton, za predhodni zadatak, evo jednog zadatka:
MIRA * MIRA (mnozenje)
---------------
****A
****R
****I
***M
------------
*******
Izvinjavam se , kako da fiksiraf pozicije teksta?
[ Daniel011 @ 10.02.2009. 23:43 ] @
MIRA * MIRA:
M=2
I=8
R=4
A=6
Ako nekog zanima, objaviću postupak (ukoliko to neko u međuvremenu ne bude učinio). Isto važi i za zadatak SEND+MORE=MONEY.
Citat: bata kg: Izvinjavam se , kako da fiksiraf pozicije teksta?
Možeš pomoću "code" tagova. [ mjux @ 11.02.2009. 14:18 ] @
RESENJE ZA MIRU
Code:
MIRA*MIRA
--------------------
****A
****R
****I
***M
--------------
*******
prvo vidimo da se radi o mnozenju sa desna u levo..
drugo vidimo da kad pomnozimo a*a dobijemo a, ili dobijemo a*a=k*10+a, gde je ka prirodan broj koji moze biti i 0.
sledece isisujemo sve moguce kombinacije mnozenja a*a
1*1=1=0*10+1 X (1 otpada zbog prvog mnozenja, kada bi a bilo 1 rezultat prvog mnozenja ne bi imao 5 cifara)
2*2=4=0*10+4 X
3*3=9=0*10+9 X
4*4=16=1*10+6 X
5*5=25=2*10+5 ----potencijalna vrednost
6*6=36=3*10+6 --- potencijalna vrednost
7*7=49=4*10+9 X
8*8=64=6*10+4 X
9*9=81=8*10+1 X
___________________________________________________________
dalje gledajuci izraz primecujemo da je R*A=k*10+R, I*A=k*10+I, M*A=k*10+M
_____________________________________________________________
ispitujemo za obe mogucnosti a;
1*5=0*10+5 X
2*5=1*10+0 X
3*5=1*10+5 X
4*5=2*10 X
5*5=2*10+5 X
6*5=3*10 X
7*5=3*10+5 X
8*5=4*10 X
9*5=4*10+5 X
u slucaju da je A=5 otpadaju sve kombinacije jer jedina kombinacija koja zadovoljava uslov je 5*5,
a ona je nemoguca posto je A=5.. iz toga zakljucujemo da A!=5
__________________________
proveravamo za A=6
1*6=0*10+6 X
2*6=1*10+2------R=2 ili I=2 ili M=2
3*6=1*10+8 X
4*6=2*10+4------R=4 ili I=4 ili M=4
5*6=3*10 X
6*6=3*10+6 X
7*6=4*10+2 X
8*9=4*10+8-------R=8 ili I=8 ili M=8
9*6=5*10+4 X
S obzirom da se pri mnozenju sa M dobija najmanji rezultat(cetverocifren naspram ostalih petocifrenih),
zakljucujemo da je M najmanji od 3 broja, tj M=2....
sada dobijamo 2 kombinacije MIRA=2486 i MIRA=2846
isprobamo prvu kombinaciju
2486*2489
------------------
14916
19888
9944--------kombinacija otpada jer je pri mnozenju sa i cetverocifren rezultat
proveravamo drugu kombinaciju
2846*2846
----------------
17076
11384
22768
5692
--------------
8099716
zakljucujemo da je kombinacija MIRA=2846 ispravna i da zadovoljava sve uslove
stoga M=2, I=8, R=4, A=6... evo moj mali doprinos ovoj temi :D [ bata kg @ 11.02.2009. 17:31 ] @
Rasporediti brojeve od 1 do 16 u "magicni kvadrat" 4 x 4 tako da zbir brojeva u svakom redu, koloni i dijagonali bude isti.(naravno prvo se mora naci koliki treba biti zbir)
........Daniel011....mali savet, velika pomoc.Hvala na razumevanju!
[ ptak 13. @ 11.02.2009. 18:38 ] @
Ovo su moja resenja...moze jos sigurno !?
 [ ptak 13. @ 11.02.2009. 18:43 ] @
Kako resiti ovo. kako poredjati tackice ispod crte da zajedno sa gornjim tackicama cine matricu 4x4.....?Samo njih pomeramo ! ! !
 [ Daniel011 @ 11.02.2009. 18:58 ] @
Ovako kako si postavio zadatak, vrlo je jednostavno dokazati da je to nemoguće izvesti. 
Za matricu 4x4 je potrebno 4*4, odnosno 16 tačkica. Na slici koju si priložio, nalazi se 3*4, odnosno 12 tačkica (9 iznad i 3 ispod crte). Prema tome, jednostavno nemamo na raspolaganju dovoljan broj tačkica da bismo bilo kakvim premeštanjem mogli oformiti 4x4 matricu. [ Zoran Milovanovic @ 11.02.2009. 19:03 ] @
Mozda ne mora da bude ispunjena tackicama? :) Mozda moze da fali ponegde :)
[ Daniel011 @ 11.02.2009. 19:06 ] @
To i ja na tren pomislih, ali su u tom slučaju moguća rešenja suviše očigledna.  [ ptak 13. @ 11.02.2009. 21:12 ] @
I meni je nemoguce delovao pa sam proverio, i izvinjavam se. Nisu u pitanju tackice vec sibice/palidrvca.
A raspored je isti kao sa tackicama, samo sto su palidrvca u pitanju.....Ja i dalje ne vidim resenje ?!   [ galet@world @ 11.02.2009. 21:30 ] @
Možda ovako:
[ ptak 13. @ 11.02.2009. 22:06 ] @
Hm zanimljivo, mozda ima jos koje resenje :D ?!
Svaka cast ! ! !
[ Daniel011 @ 12.02.2009. 00:08 ] @
@galet@world Nisam siguran jesam li dobro skapirao tvoje rešenje, ali ne znam gde ti je nestalo ono palidrvce iz drugog reda odozgo, u sredini. Tu imaš samo prazninu. A u zadatku je rečeno da se smeju premeštati isključivo palidrvca koja se nalaze ispod crte, a ne i palidrvca iznad crte?
Da pokušam i ja. Pošto je u zadacima koje postavlja ptak 13. sve uvek nekako u domenu nagađanja,  ja bih, recimo, pretpostavio da je možda početna situacija kao ova prikazana na slici:
E, u tom slučaju bi rešenje možda moglo izgledati ovako:
 [ galet@world @ 12.02.2009. 12:04 ] @
Ovo tvoje ne mogu da otvorim - dobijem "connection onterupted"
pretpostavljam da si krstiće stavio po dijagonali, ali zadatak je ipak malo
neodređen jer kroz dva krstića prolaze po dve linije a kroz srednji četiri,
osim ako nisi rešio nekako drukčije.
u svakom slučaju u pravu si jer ja nisam obratio pažnju na uslov u
zadatku da se samo tri šibice mogu pomerati.
[ Daniel011 @ 12.02.2009. 12:25 ] @
Čudi me da ne možeš da otvoriš - ja sam isprobao i iz Firefoxa i iz Opere i iz IE-a i radi iz sva tri browsera.
Možeš li da otvoriš ove linkove ka Imageshack-u?
Početno stanje
Rešenje[ ptak 13. @ 12.02.2009. 13:55 ] @
Ja sam dosao do resenja da krstice poredjam po dijagonali, onda se dobija 4x4....I izgleda ovako
Citat: Daniel011:
Da pokušam i ja. Pošto je u zadacima koje postavlja ptak 13. sve uvek nekako u domenu nagađanja, 
Ja se izvinjavam, ali radi se o tome da cujem zadatak a onda moram naci sam resenje, pa kad nadjem ja ga objavim, ali eto par zadataka su ispala nagadjanje sobzirom da ja sam nisam znao resenje.....Izvinjavam se....trudicu se da ubuduce budu preciznije formulisani zadaci koje postujem.
Hvala ! ! ! [ galet@world @ 12.02.2009. 18:59 ] @
Citat: Daniel011: Čudi me da ne možeš da otvoriš - ja sam isprobao i iz Firefoxa i iz Opere i iz IE-a i radi iz sva tri browsera.
Ne znam šta je u pitanju, ali kad sam hteo da otvorim nije moglo, a sad vidim sliku odmah,
Verovatno sam upao u vreme kad si i ti radio pa još nisi bio dovršio,
Pretpostavio sam da si uradio upravo ovo što ja ptak 13. pokazao, ali ne ovako
jer ne vidim matricu 4 x 4 već 3 x4 po horizontali i 3 x 4 po vertikali, nego ovako,
ali i ovo ima nedostataka [ Daniel011 @ 12.02.2009. 21:30 ] @
Citat: galet@world: jer ne vidim matricu 4 x 4 već 3 x4 po horizontali i 3 x 4 po vertikali
Na toj slici koju sam priložio kao rešenje, ja sam zamislio da šibice zapravo predstavljaju "pregrade" između polja matrice, tj. da je potrebno imati 3 pregrade po horizontali i 3 po vertikali, kako bismo imali 4x4 polja, odnosno 4x4 matricu.
Mada, priznajem, potrebno je baš, baš dosta mašte da bi se, gledajući tu sliku, mogla na taj način zamisliti 4x4 matrica.  Zato uopšte i ne tvrdim da je moje rešenje ono pravo. 
Nego, ako možete ili ti ili ptak 13. da mi protumačite vaša rešenja, ovo i ovo (između kojih ne uočavam neku bitnu razliku). Evo gledam već duže vreme i ma koliko da sam se trudio da na tim slikama pronađem 4x4 matricu, ja vidim samo 3x3 matricu kod koje se na glavnoj dijagonali nalaze po dve šibice (međusobno prekrštene), a na preostalim poljima je po jedna šibica. Kako treba da posmatram te slike da bih video 4x4 matricu? [ ptak 13. @ 12.02.2009. 22:09 ] @
Pa sta ja znam....ja sam shvatio kao brojanje sibica po X i Y osi, i svude ih ima po 4. Cak je i profesorka matematike danas saopstila da je to resenje zadatka.....nadam se da ti je sad jasno  [ Daniel011 @ 12.02.2009. 22:16 ] @
Ček', da li bih onda, po toj istoj logici, mogao za matricu

da kažem da je to matrica 4x4, s obzirom da je zbir u svakoj vrsti i u svakoj koloni jednak 4? 
Svejedno, hvala na pojašnjenju.  [ galet@world @ 14.02.2009. 09:49 ] @
Izgleda da ipak postoji korektno rešenje
[ ptak 13. @ 14.02.2009. 11:29 ] @
Citat: galet@world: Izgleda da ipak postoji korektno rešenje
A zasto meni ovo ovde tvoje resenje nije nista jasno  
Salim se, aj pojasni malo....zanimljivo deluje.... [ galet@world @ 14.02.2009. 13:21 ] @
Prema tvojoj slici postavljanje palidrvaca tačno jedno ispod drugog ne mora da se podrazumeva
kao početno stanje. Ja sam to protumačio kao malo smaknute redove nadesno, a ako neko
hoće može početno stanje postaviti i drukčije - važno je da palidrvca ostanu u pravougaonicima
u kojima si ti nacrtao tačke. Možda ima i drugih rešenja. Evo slike sa "stvarnim" palidrvcima:
[ bata kg @ 14.02.2009. 17:39 ] @
Evo jos jednog magicnog kvadrata. Ako ga resavate na "probu", bice malo poteze.
.
.................Napraviti mag.kv. 5 x 5 ciframa od 1 do 25(kolone,redovi,dijagonale)
[ ptak 13. @ 14.02.2009. 19:59 ] @
Citat: bata kg: Evo jos jednog magicnog kvadrata. Ako ga resavate na "probu", bice malo poteze.
.
.................Napraviti mag.kv. 5 x 5 ciframa od 1 do 25(kolone,redovi,dijagonale)
Aha kolne redovi dijagonale ali koliki je zbir po koloni, dijagonali ili redu ? resava se na zbir ?! [ Daniel011 @ 14.02.2009. 21:31 ] @
Pa treba sâm da izračunaš koliki je zbir po vrstama, kolonama i dijagonalama. U zadatku je dato sve što je potrebno. 
Hint: Suma aritmetičkog niza.  [ bata kg @ 14.02.2009. 21:49 ] @
Ako uspes da mag.kv. "provalis" resavanje se pretvara u primenu odredjenog matematickog postupka.
Pitanje kolika je suma isto tako.
tesko je samo ono sto se nezna
[ galet@world @ 17.02.2009. 15:02 ] @
Evo rešenja:
[ peka @ 19.02.2009. 17:00 ] @
Evo jedan malo tezi :)
Code:
Zadatak:
Na ostrvu je grupa ljudi. Niko od njih ne zna boju svojih ociju,
ali moze da vidi oci svih ostalih stanovnika ostrva. Niko ne
smije da kaze nekom drugom boju njegovih ociju niti da mu
prenese neku informaciju na bilo koji nacin. Na ostrvo svake
noci u ponoc pristaje brod i svako ko zakljuci boju svojih
ociju moze da ode sa ostrva (a svi zele da odu sa ostrva).
Svi su savrseni logicari i znaju ova pravila.
E sad, na ostrvu je 100 osoba sa plavim ocima, 100 osoba
sa zelenim ocima i jedna osoba (zvacemo je Guru) sa
smedjim ocima (ali ostrvljani ne znaju koliko koga ima, s tim
da naravno, mogu da zakljuce koliko ih je ukupno).
Jednog dana je Guru dobio dozvolu da se
obrati svima, samo jednom, recimo u podne. Guru je
rekao: "Vidim nekoga sa plavim ocima".
Ko napusta ostrvo i posle koliko dana?
Hint: odogovor nije "niko ne napusta ostrvo". :)
[Ovu poruku je menjao peka dana 19.02.2009. u 18:38 GMT+1][ sanja2010 @ 19.02.2009. 17:17 ] @
Verovatno gresim jer ne koristim Guruovo objasnjenje, ali zar ne mogu svi da prebroje koliko ima onih sa zelenim, a koliko onih sa plavim ocima? Ako osoba x izbroji 99 plavookih i 100 zelenookih, onda ta osoba ima plave oci. Slicno, ako izbroji 99 zelenih i 100 plavih, zna da ima zelene oci. Tako svi mogu istog dana da napuste ostrvo :)
[ peka @ 19.02.2009. 17:36 ] @
U zadatku ne pise da oni znaju koliko ima osoba sa plavim a koliko sa zelenim ocima. Tako da ta osoba koja vidi 99 plavih, ne zna da li ukupno ima 99 ili 100 plavih.
P.S. Prepravio sam zadatak da bi to bilo jasnije.  [ braker @ 19.02.2009. 19:02 ] @
Ako su savrseni logicari, stoti dan ce shvatiti svih 100 da im je vreme ici, ne?
[ peka @ 19.02.2009. 23:50 ] @
Kojih 100? Ima ih 201 ukupno  [ Shadowed @ 20.02.2009. 01:08 ] @
Paa.. Ako im je poznato da postoje oni sa plavim, oni sa zelenim i oni sa smedjim ocima, Guru ce videti da niko nema smedje od drugih, tako da ih mora imati on (jer zna da neko ima). Tako on moze odmah ici, samo sto mi ovo deluje suvise lako...
[ peka @ 20.02.2009. 01:21 ] @
Ne, nije im poznato da neko mora da ima smedje oci. Poznato im je samo ono sto pise u prvom pasusu. Procitaj malo bolje.  [ braker @ 20.02.2009. 10:48 ] @
Sudeci po recima Gurua, svih 100 plavookih sasvrsenih logicara napustice ostrvo 100-tog dana :-).
Recimo, da je na ostrvu 5 plavookih, i posle 4 dana niko ne napusti ostrvo, svako od njih 5 na osnovu preostale 4-ice moze zakljuciti da ima plave oci - pa ce 5-ti dan svi napustiti ostrvo.
[ Tea94 @ 20.02.2009. 11:18 ] @
pa, da su logicari, ogledali bi se u vodi, i time zakljucili boju svojih ociju. znaci svi bi napustili ostrvo istog dana.
[ peka @ 20.02.2009. 12:58 ] @
@Tea94
Pa ok, ali rjesenje je cisto logicko, znaci nije u pitanju neka caka tipa gledanje odraza u vodi, ili da izvade jedno oko i sl.
@braker
To jeste rjesenje, ali ajde ga malo obrazlozi. Ako ih je 5, kako neko moze posle 4 dana da zakljuci da ih ima 5 ukupno?
[ zzzz @ 20.02.2009. 13:11 ] @
Treba poći sa razmatranjem šta bi svaki od njih zaključio da ih je po jedan plavi,
jedan zeleni +guru.
A onda razmotriti kako bi razmišljali da ih je 2p+2z+g.
Zatim za slučaj 3p+3z+g.
------------
Uočiti pravilo i to je to.
[ galet@world @ 20.02.2009. 14:49 ] @
A da li smeju da se dogovaraju, na primer, za tu priliku kad Guru dobije reč da se dogovore da svi koji vide plavu boju zažmure.
Budući da svi ne mogu istovremeno zažmuriti mora jedan ostati poslednji i taj više ne vidi nikakvu boju osim boju Guruovih očiju
a one nisu plave. Prema toma taj čovek gleda ima plave oči jer Guru ne vidi nikom oči osim tom poslednjem čoveku koji gleda
i koji onda zna kakve su mu oči
[ Daniel011 @ 20.02.2009. 15:54 ] @
Rešenje koje je ponudio braker, a razjasnio zzzz, zaista izgleda logično.
Međutim, ako bih ja to posmatrao na ovaj način:
Svaki od 100 plavookih ostrvljana vidi 99 plavookih, pa samim tim zna da Guru vidi ili 99 ili 100 plavookih. Prema tome, to što je Guru rekao "Vidim nekoga sa plavim očima" za njih ne predstavlja ama baš nikakvu novu informaciju.
Gde ja, sa ovakvim razmišljanjem, pravim grešku?
[ braker @ 20.02.2009. 20:27 ] @
Moras se postaviti u ulogu savrsenog ostrvskog logicara i poci od pretpostavke da imas plave oci, nadajuci se da je tacna :-)
[ zzzz @ 20.02.2009. 22:17 ] @
Kada je guru rekao "vidim nekog sa plavim očima" tada je svaki od onih 100 sa plavim očima
pomislio:
1)Da nije ovih prokletih 99 koje vidim sa plavim očima znao bih da sam taj ja i noćas bih otputovao.
Svaki od ovih sa zelenim očima je slično mislio samo što je vidio pred sobom prokletih 100 sa plavim
očima.(Ostavimo zasad zelene i njihov način razmišljanja jer su u nešto težoj situaciji.)
2)Svi dalje razmišljaju ovako:Ma i kad bih vidio jednog plavog lako bih.Jer ako sam ja zelen, on bi znao
da je jedini plav pa bi noćas otišao, a ja bih sutra bar znao da sam zelen.Ali ako ne otputuje to
je samo zato što sam i ja plav.Tada bih ja drugu veče otišao na brod, a to bi uradio i ovaj drugi
sa plavim očima jer zaključuje isto.
3)Kad bi umjesto ovih prokletih 99 bila samo dva plava ja bih opet imao šansu.Pustio bih da
razmišljaju kao u tački 2) pa ako odu drugu veče onda sam ja nažalost zelen kao i svi koji su
ostali.Ali ako nisu otišli to znači da svaki od njih vidi isto kao ja dvojicu plavih.Ja, i njih dva bi
treću veče išli na brod.
4)Ni za viđena tri (umjesto 99) sa plavim očima nije problem.Pustim da misle kao pod 3) pa ako
treću veče odu nek im je sretno.A ako ne odu pakujem se i ja s njima četvrtu veče jer sam plav.
------------- (malo odmora pa ćemo dalje do 100) ---------------
n)Ako bi ih umjesto 99 sa plavim očima bilo manje, recimo (n-1), pustio bi ih da razmišljaju kao u
tački (n-1), pa ako ne otputuju (n-1) veče, pakujem se i n tu veče ide svih nas n komada.
------------- (da preskočimo malo ovih tačaka radi štednje?) ----------------
100)Ako ih vidim 99 sa plavim očima pustio bi ih da misle kao u tački 99) (nažalost preskočena
ali zna se šta bi pisalo!), pa ako ne otputuju 99-tu veče idem sutra i ja.Nas 100 odosmo 100-tu
veče.
Da ne zaboravimo zelene koji su ostali jer su na neki način izmanipulisani od gurua.Svaki od njih
100 je razmišljao na isti prethodni način.čekao 100 ti dan nadajući se da te večeri neće plavi otići
već će se i on priklučiti 101-vu veče i ostaviti preostalih 99 zelenih koje vidi.
Ovaj zadatak, ako je tačno riješen, otvara jednu misterioznu nejasnoću koju je spomenuo Danijel011.Kakvu to moć ima GURU.Svi su znali (i plavi i zeleni) da će doći i reći "vidim tu i tu boju očiju".Svi vide i plave i zelene oči oko sebe, a znaju i da GURU to vidi.Može lupiti šta hoće,vrlo važno i ko ga šiša šta je rekao,
jer to nije ni za koga novost vrijedna pažnje.Kako je uspio bezveznom izjavom upropastiti zelenooke?
Ko zna objašnjenje?
[ Marko Enter @ 21.02.2009. 00:05 ] @
Hmmm, izgleda zanimljivo ovo sa plavookima i zelenookima 
pozdrav
Marko [ Daniel011 @ 21.02.2009. 00:34 ] @
Citat: zzzz: Ovaj zadatak, ako je tačno riješen, otvara jednu misterioznu nejasnoću koju je spomenuo Danijel011.Kakvu to moć ima GURU.Svi su znali (i plavi i zeleni) da će doći i reći "vidim tu i tu boju očiju".Svi vide i plave i zelene oči oko sebe, a znaju i da GURU to vidi.Može lupiti šta hoće,vrlo važno i ko ga šiša šta je rekao,
jer to nije ni za koga novost vrijedna pažnje.Kako je uspio bezveznom izjavom upropastiti zelenooke?
Ko zna objašnjenje?
Ja ne znam objašnjenje, ali me ovaj zadatak dosta podsetio na zadatak sa osuđenikom, koji je bio postavljen na istoj ovoj temi pre tačno dve godine.
Radi se o tome, da je zatvorenik, na isti način kao u zadatku sa ostrvljanima, razmišljao induktivnim putem. To ga je dovelo do pogrešnog zaključka da neće biti pogubljen. Kasnije sam tražio na Googletu taj zadatak, ne bih li saznao gde je greška u takvom razmišljanju, ali sam našao samo odgovor kako taj zadatak spada u tzv. "nerešive" zadatke (u smislu, da niko do sada nije ponudio adekvatan odgovor) i da je to dobar primer kako induktivno razmišljanje, iako je svaki korak sâm po sebi korektan, u celini može biti pogrešno.
Možda je to upravo slučaj i u našem zadatku sa ostrvljanima, a da tačan odgovor ipak glasi da niko ne napušta ostrvo?  [ Bojan Basic @ 21.02.2009. 01:56 ] @
Citat: zzzz:
Ovaj zadatak, ako je tačno riješen, otvara jednu misterioznu nejasnoću koju je spomenuo Danijel011.Kakvu to moć ima GURU.Svi su znali (i plavi i zeleni) da će doći i reći "vidim tu i tu boju očiju".Svi vide i plave i zelene oči oko sebe, a znaju i da GURU to vidi.Može lupiti šta hoće,vrlo važno i ko ga šiša šta je rekao,
jer to nije ni za koga novost vrijedna pažnje.Kako je uspio bezveznom izjavom upropastiti zelenooke?
Ko zna objašnjenje? Citat: Daniel011:
Prema tome, to što je Guru rekao "Vidim nekoga sa plavim očima" za njih ne predstavlja ama baš nikakvu novu informaciju.
Predstavlja novu informaciju. Zamislimo, pojednostavljenja radi, da umesto s brojem 100 radimo s brojem 2. Onog momenta kada guru izgovori svoju rečenicu, svi ostrvljani imaju novu informaciju da svi ostrvljani znaju za postojanje osobe s plavim očima. Drugim rečima, i pre nego što je guru konstatovao da na ostrvu postoji plavooka osoba, svi su to znali (dve plavooke osobe su primećivale jedna drugu, svi ostali su primećivali njih obe), ali nisu znali da li i ostali raspolažu tom informacijom (a od momenta guruovog govora to postaje fakat, jer je on upravo to podelio sa svima). [ Daniel011 @ 21.02.2009. 02:17 ] @
Da, sve to što si napisao je sasvim tačno za slučaj sa dve plavooke osobe, koji si razmatrao. Međutim, u slučaju 100 plavookih osoba, tvoj drugi deo rečenice
Citat: ali nisu znali da li i ostali raspolažu tom informacijom
prestaje da bude tačan, jer tada svaki ostrvljanin zna da i svi ostali vide bar 98 plavih, tj. da raspolažu tom informacijom. [ zzzz @ 21.02.2009. 09:41 ] @
Ja podržavam mišljenje:
Citat: Daniel011: Međutim, u slučaju 100 plavookih osoba, tvoj drugi deo rečenice
prestaje da bude tačan, jer tada svaki ostrvljanin zna da i svi ostali vide bar 98 plavih, tj. da raspolažu tom informacijom.
A mislim da Bojan griješi jer misli da zna šta će GURU tada reći:
Citat: Bojan Basic: Predstavlja novu informaciju. Zamislimo, pojednostavljenja radi, da umesto s brojem 100 radimo s brojem 2. Onog momenta kada guru izgovori svoju rečenicu, svi ostrvljani imaju novu informaciju da... .
Sama riječ GURU (koji nije dao baš nikakvu novu informaciju za naš
slučaj 100P+100Z) u našu podsvjest servira jednu dogmu.Njegovu izjavu: "ja vidim plave oči" instiktivno smatramo nepromjenjivom istinom u koju ne smijemo sumnjati i preispitivati.A treba.
Ne mislim da on laže, ali odakle nam zaključak da će on baš takvu rečenicu uvjek reći.To je ona situacija na početku kad plavi misli da kad bi uklonili onih 99
ostalih sa plavim očima, nebi mu bilo teško pogoditi da je on upravo taj plavi.
Dozvolimo da GURU može u toj situaciji izreći zelenu boju, jer ako ih je 101 takvih
moraće da ne bi lagao.A kako onda dalje?
Rješenja izgleda nema pa su na žalost još uvijek svi zarobljeni na onom ostrvu.
[ sanja2010 @ 21.02.2009. 10:24 ] @
Ja ne shvatam bas najbolje to oko gurua. Guru samo jednog dana dodje i obnaroduje da vidi nekog s plavim ocima ili svakog dana kaze da li vidi ili ne vidi? Ako je ovo prvo slucaj, i dalje ne uspevam da vidim kako ta informacija koristi ostrvljanima, a ukoliko je ovo drugo, zadatak je lak... Svakog dana je samo jedan ostrvljanin okrenut licem guruu, on sazna svoju boju ociju i uvece ide.
[ braker @ 21.02.2009. 10:41 ] @
Ali ja uzimam u obzir mogucnost da sam bas ja taj koga je guru video, i znam da u slucaju da imam plave oci, sigurno napustam ostrvo. U zadatak je trebalo uvrstiti sankcije za pokusaj ukrcavanja u slucaju izvodenja pogresnog zakljucka - recimo, odrubljivanje glave :-) Tada, pretpostavka na osnovu izjave gurua ima tezinu, i drugacijim pristupom logicar se igra s' glavom :-)
[ ptak 13. @ 21.02.2009. 11:04 ] @
Ja licno mislim da jedino prihvatljivo to da se ogledaju u vodi, ima vise razloga za to:
1-Savrseni logicari
2-Zasto su bas na ostrvu ( ostrvo je kopno okruzeno VODOM ) zasto nisu u sumi, pustinji......
@Peka daj odgovor......?!
[ peka @ 21.02.2009. 15:05 ] @
Kao sto sam vec rekao u prethodnoj poruci, odgovor nije da su se ogledali u vodi, i slicni trikovi, nego je u pitanju cisto logicko razmisljanje i zakljucivanje ostrvljana. Znaci, posmatramo jednu idealizovanu situaciju.
Odgovor koji je zzzz dao je u potpunosti tacan, a napisacu i malo drugacije rjesenje koje ce, nadam se, dati odgovor na pitanje: "Koju novu informaciju je Guru dao?". Problem je dosta tezi nego sto se cini na prvi pogled, jer nije samo bitno sta neko zna, nego sta neko zna o tome sta neko drugi zna ("ja znam da ti znas"), i tako 99 puta u dubinu ("ja znam da ti znas da on zna", itd).
Osoba sa plavim ocima (bilo koja posto su svi ekvivalentni), zvacemo je Broj1, moze da pretpostavi jedan od dva slucaja:
1. da ima plave oci
2. da nema plave oci
(ipak je Broj1 savrseni logicar  )
Ako je tacno pod 1. onda Broj1 ide sa ostrva, ali posto mora biti siguran, mora da razmotri drugu mogucnost, a to je da nema plave oci, dakle da ima 99 osoba sa plavim ocima. Sada Broj1 posmatra proizvoljnu osobu iz te grupe, zvacemo je Broj2, i pretpostavlja tok razmisljanja te osobe.
Sada taj "zamisljeni" Broj2, razmatrajuci 2 opcije na isti nacin, isto mora da pretpostavi da nema plave oci, sto znaci da ima 98 osoba sa plavim ocima, pa pretpostavlja tok razmisljanja neke od tih 98 osoba (Broj3). E sad, ovo razmisljanje Broja2 je naizgled besmisleno, jer svi na ostrvu znaju da postoji bar 99 osoba sa plavim ocima. Ali, radi se o hipotetickom razmisljanju neke osobe u slucaju da Broj1 nema plave oci, sto znamo da nije tacno. Znaci, niko na ostrvu nece ovako razmisljati (kao Broj2), ali Broj1 zna da bi neko tako razmisljao u slucaju da on nema plave oci, sto je opcija koju mora da razmotri. I sva razmisljanja u nastavku su hipoteticka, tj. nece se nikad desiti, jer predstavljaju razmisljanja koja polaze od pogresnih pretpostavki (mi znamo da su pogresne, ali osobe koje razmisljaju o njima ne znaju).
Broj3 sada "vidi" 97 osoba sa plavim ocima, i pretpostavlja za sebe da nema plave oci, dakle ukupno je 97 plavih. Ovaj proces se dalje nastavlja (dakle, smanjuje se pretpostavljenih broj osoba sa plavim ocima), dok se ne dodje do poslednje osobe (u tom trenutku, onaj ko nju posmatra, Broj99, pretpostavlja da ima samo jedna osoba sa plavim ocima). Poslednja osoba, Broj100 nema 2 mogucnosti kao svi ostali, jer je Guru rekao da ima bar jedna osoba sa plavim ocima, a to mora biti on. (Dakle, ovde je bitna Guru-ova izjava).
Medjutim, posto Broj100 ne ode prve veceri, onda Broj99 ne moze da za sebe pretpostavi da nema plave oci, tj. mora da pretpostavi da imaju 2 osobe sa plavim ocima: on (Broj99) i Broj100. Ali, posto posle 2 dana, njih dvojica ne odu sa ostrva, Broj98 takodje ne moze da pretpostavi da nema plave oci, dan kasnije to shvata i Broj97, i tako dalje, sve dok posle 100 dana to ne shvati Broj1, koji onda odlazi sa ostrva. Posto sve osobe sa plavim ocima razmisljaju kao Broj1 (ali sada stvarno, ne hipoteticki), svi plavi odu sa ostrva posle 100 dana.
Drugi nacin da se posmatra zasto je Guru-ova izjava bitna (opet, ovo je razmisljanje neke od "plavih" osoba"):
1. Znam da je na ostrvu bar 99 osoba sa plavim ocima.
2. Znam da svako zna da je na ostrvu bar 98 osoba sa plavim ocima. (Posto ja mozda nemam plave oci)
3. Znam da svako zna da svako zna da je na ostrvu bar 97 osoba sa plavim ocima. (uff  )
...
99. Znam (da svako zna)x98 da je na ostrvu bar 1 osoba sa plavim ocima.
100. Ali NE ZNAM (da svako zna)x99 da je na ostrvu bar 1 osoba sa plavim ocima.
E sad, kad je Guru rekao da postoji bar 1 osoba sa plavim ocima, to su svi vec znali. Ali je on isto tako ubacio tu 1 osobu u sve nivoe razmisljanja (ne znam kako drugacije da se izrazim), sto je, od ovih nabrojanih izjava, imalo uticaja samo na 100-tu, koja je uticala na 99-tu (koja se mijenja u "...bar 2 osobe sa plavim ocima"), sto se dalje "odmotava" do prve koja postaje:
1. Znam da je na ostrvu bar 100 osoba sa plavim ocima. A posto ih vidim 99 ja moram biti 100-ta.
Ufff, valjda ce nekome biti jasno (vise nisam siguran ni da li je meni jasno  ).
P.S. Ono sto je jos bitno u postavci zadatka je da nije dovoljno reci da su svi savrseni logicari. Treba reci i da svi znaju da su svi savrseni logicari. I da svi znaju da svi znaju da su svi savrseni logicari. I da... Shvatili ste, tako 99 puta.  Ma, ludilo... [ peka @ 21.02.2009. 15:16 ] @
Citat: zzzz: ali odakle nam zaključak da će on baš takvu rečenicu uvjek reći.
Ne moramo mi da zakljucujemo sta ce Guru reci. Guru je rekao to sto je rekao, to je u postavci zadataka (a zasto je to rekao? ja mislim da bi nas malo za*ebavao  ). Mogao je da kaze bilo sta, npr. isto to samo za zelene, onda bi citava ova diskusija bila ista, ali samo za zelene umjesto plavih.
Citat: zzzz:
Da ne zaboravimo zelene koji su ostali jer su na neki način izmanipulisani od gurua.Svaki od njih
100 je razmišljao na isti prethodni način.čekao 100 ti dan nadajući se da te večeri neće plavi otići
već će se i on priklučiti 101-vu veče i ostaviti preostalih 99 zelenih koje vidi.
Da, ovo je tacno, ali ne znam zasto mislis da su izmanipulisani, ja mislim da je Guru onu recenicu izjavio "najdobronamjernije"  [ Bojan Basic @ 21.02.2009. 17:15 ] @
@Daniel 011, zzzz:
Primer sa dve osobe sam naveo kako bih ilustrovao da nova informacija nije nužno postojanje osobe s plavim očima, već se iz Guruove rečenice iščupati još saznanja. Mislio sam da će, ako se to usvoji, biti lako nadograditi moj primer do sto osoba (ili koliko ih god ima). No, ako nisam bio dovoljno jasan, pokušaću da se dopunim.
Pretpostavimo da postoje tri zelenooke osobe. Tada, jasno, nova informacija nije „svi ostrvljani znaju za postojanje osobe s plavim očima“ (što ste obojica ispravno primetili, ali to nisam ni pokušao da kažem). Međutim, i dalje svim ostrvljanima guruova rečenica daje novu informaciju, sledeću: „svi ostrvljani znaju da svi ostrvljani znaju za postojanje osobe s plavim očima“.
Jasno je zašto je ova rečenica tačna informacija. Pogledajmo zašto je nova. Vratimo se u vreme pre guruovog govora, i neka su zelenooke osobe Aca, Bane i Crni. Aca razmišlja ovako: „Moguće je da ja imam zelene oči. U tom slučaju bi Bane, videvši samo još Crnog s plavim očima, razmišljao ovako: ’Ukoliko ja imam zelene oči, Crni ne bi znao postoji li na ostrvu osoba s plavim očima’.“ Dakle, Aca ne može biti siguran da svi ostrvljani znaju da svi ostrvljani znaju za postojanje osobe s plavim očima, jer je Bane u ovom slučaju kontraprimer (budući da Bane ne zna da li svi ostrvljani znaju za postojanje osobe s plavim očima, konkretno ne zna da li Crni zna za postojanje osobe s plavim očima).
Da li je ovim razjašnjeno šta je nova informacija ukoliko postoje tri plavooke osobe? Ako jeste, odavde bi trebalo da stvarno bude jednostavno uopštiti celu priču do 100 osoba s plavim očima (u informaciju iz ovog primera samo treba ubaciti „...da svi ostrvljani znaju...“ još 97 puta, i to će biti nova informacija ukoliko ima 100 osoba s plavim očima).
Citat: zzzz:
Ne mislim da on laže, ali odakle nam zaključak da će on baš takvu rečenicu uvjek reći.
Nigde nisam pretpostavljao da se unapred zna šta će guru reći (na šta se već peka osvrnuo). [ Daniel011 @ 21.02.2009. 21:57 ] @
@peka, Bojan Basic
U pravu ste. Hvala obojici na iscrpnom objašnjenju.
Stvarno jedan od najinteresantnijih zadataka koje sam video.  [ Tea94 @ 21.02.2009. 23:17 ] @
ovo je zadatak postavljen na prijemnom za OKSFORD. Ko ga resi-upisuje se odma.
1=5
2=25
3=325
4=4325
5=?
[ sanja2010 @ 21.02.2009. 23:36 ] @
Ma da, nije valjda da verujes u te urbane mitove, da tako upisu ljude na jedan od najjacih uni-ja na svetu na osnovu jednog zadatka :)
Inace, u ove kasne sate, ja tipujem na 54325, ali verovatno gresim ;)
[ Bojan Basic @ 21.02.2009. 23:52 ] @
Ne, odgovor je 5 = 1 (jer je već dato 1 = 5, a jednakost je simetrična  ), a ni ja ne podnosim te priče „ovaj zadatak je postavljen tamo i tamo“, „može da ga reši samo toliko i toliko procenata ljudi na svetu“ i sl. [ Daniel011 @ 22.02.2009. 00:07 ] @
Nisam nešto siguran da ovde znak "=" označava relaciju jednakosti, s obzirom da se u zadatim izrazima sa leve i desne strane tog znaka nalaze očigledno nejednake vrednosti. A ako "=" označava neku relaciju koja nije jednakost, zbog čega bi ta relacija nužno morala biti simetrična?  [ Tea94 @ 22.02.2009. 00:17 ] @
u jbt al ga iskomplikuje... pa jednostavno zamisli kao da imas:
A=B
C=D
E=F
B=?
 [ Bojan Basic @ 22.02.2009. 00:28 ] @
Citat: Daniel011:
Nisam nešto siguran da ovde znak "=" označava relaciju jednakosti, s obzirom da se u zadatim izrazima sa leve i desne strane tog znaka nalaze očigledno nejednake vrednosti. Citat: Tea94:
pa jednostavno zamisli kao da imas:
A=B
C=D
E=F
B=?
Vidiš? 
Uzgred, drago mi je što smo se konačno sporazumeli oko onog ostrva, a i dalje nestrpljivo očekujem šta će zzzz da kaže. S obzirom na žar s kojim se uključivao u ovu raspravu, ne znam je li zaboravio da je pre skoro pet i po godina na istom ovom forumu upravo on postavio gotovo identičan zadatak (samo je „okruženje“ drugačije), ili je nešto drugo posredi.  [ zzzz @ 22.02.2009. 02:18 ] @
Još malo o plavookim,zelenookim i GURUU!(izvini Tea94 zbog upada u tvoj zadatak.)
-Malo moje teorije o informacijama:
1)Informacija ne vrijedi pišljiva boba ako je niko ne zna!
2)Ako svi znaju informaciju onda je nemaš kome prodati-dakle: vrijedi još manje.
3)Informacija je i vremenski ovisna, prvi koji je saznaju mogu je prodati onima koji će je
kasnije saznati, a oni koji je zadnji kupuju, kada je već svi ostali znaju uzalud bacaju lovu.
Moramo ovdje poći od informatike, i pitanja da li je gospodin GURU svojom izjavom
"vidim plave oči" poboljšao informatičko saznanje bar za nekog.Ipak (iako nerado) priznam da jeste.
Kako?
Ajmo početi od jednostavnih zadataka:
1) Imamo 1 plavooki+100 zelenookih.Saslušaju oni svi GURUA koji kaže: "Vidim plave oči".
Ta informacija je prava samo za plavookog koji se odmah pakuje i ode na brod zato što ne vidi
ni jednog drugog konkurenta sa takvim očima.A za ostalih 100 ona će biti prava tek sutra kad primijete
da nema onog plavog.
GURU je očito pomogao onom plavookom!, ali i svim zelenookim samo kasno za jedan dan.Slaba utjeha, jebeš takvu informaciju.
2)Malo teži zadatak: Imamo 2 P+100 Z.I ako Guru kaže opet isto.Naguliće ova dvojica drugu veče na brod, a
tek prekosutra će ostali zelenooki shvatiti koja je boja njihovih očiju.
3)Još malo teži zadatak:-------------------(nastaviću za koji dan)
[Ovu poruku je menjao zzzz dana 22.02.2009. u 04:25 GMT+1]
[ zzzz @ 22.02.2009. 03:12 ] @
Odgovor Bojanu
Jesam zaboravio jer nisam originalan autor.Fala.
Gledam sad nešto tu temu.Vidim da si rješio zadatak.Odmah sam znao
da ćeš kad tad diplomirati PMF, ako već nisi.Onaj zadatak nisam izmislio
ja već jedna moja dobra prijateljica, matematičarka.Baš izmislila, a ne
preštancala odnekud.Ja sam samo promijenio originalnu priču ne navodeći
izvor, a srž problema je ostao isti.I to baš u onoj kafani blizu skupštine
u ulici kneza Miloša gdje je i pokojni Tin Ujević često pio vino.
U BG je nekad bila divna kafana,
Ako se ne varam zvala se "Tri lista duvana".
Unutra je bilo i gospode i bijede,
Neki sjede i misle, a neki samo sjede.(ja)
-Volim ovakve probleme jer u rješavanju mogu učestvovati
doktori matematike, a ravnopravno sa njima čak i nepismeni ljudi.
[ galet@world @ 22.02.2009. 17:50 ] @
Niko ne misli na Gurua. Kako će on saznati boju svojih očiju, ili će ostati trajno na ostrvu?
I ja sam nešto pokušao
[ galet@world @ 25.02.2009. 20:32 ] @
Citat: zzzz:
1) Imamo 1 plavooki+100 zelenookih.
2)Malo teži zadatak: Imamo 2 P+100 Z.I ako Guru kaže opet isto.
3)Još malo teži zadatak:-------------------(nastaviću za koji dan)
Budući da nisi nastavio - ja bih ako se ne ljutiš - šteta je da rešenje ostane nedorečeno.
Mislim da je nastavljanje sa sve težim zadacima nepotrebno.
Rešenje je (čini mi se) vrlo jednostavno i svi idu kući isti dan. Evo:
Neka se jedan plavooki logičar zove Janko.
On vidi 100 zelenookih i 99 plavih, a ne zna kakav je on. On kupi 99 sunčanih naočara i podeli ih plavookim,
zatim dođe do Gurua koji kaže "Ja vidim plavu boju", a zauzvrat Janko kaže "Ja vidim smeđu boju" i gotovo.
Sad svi znaju sve. I svi idu kući isti dan.
Kako? Svim plavookim logičarima sa naočarima je jasno šta je Janko hteo jer tako bi postupili i sami kad bi
hteli da saznaju boju svojih očiju. Zelenima je takođe jasno da Janko neće staviti naočare ni jednom zelenookom.
Janko i svaki koji ima naočare je plavook, ko nema naočare taj je zelenook. Jedini Guru ne vidi smeđu boju
pa je on taj.
Ispravite me ako grešim!
[ galet@world @ 25.02.2009. 20:49 ] @
A sad evo jednog zadatka koji je zadavan na raznim forumima pa i ovde negde, ali ga niko nije uspeo da reši.
Zadat je prav ugao, dužina hipotenuze i položaj neke tačke kroz koju ta hipotenuza treba da prođe.
Treba konstruisati trougao.
[ bata kg @ 25.02.2009. 21:37 ] @
Nacrtati neku tacku i "kroz nju" nacrtati datu hipotenuzu.
Prav ugao dobijamo iz " periferni ugao iznad precnika"
.
.
Mozda malo nejasno, da ne pokvarim uzivanje ostalima.
[ galet@world @ 26.02.2009. 13:09 ] @
Možda nisi obratio pažnju da je položaj tačke zadat (u ravni između krakova pravog ugla)
[ peka @ 26.02.2009. 13:45 ] @
Citat: galet@world: On vidi 100 zelenookih i 99 plavih, a ne zna kakav je on. On kupi 99 sunčanih naočara i podeli ih plavookim,
zatim dođe do Gurua koji kaže "Ja vidim plavu boju", a zauzvrat Janko kaže "Ja vidim smeđu boju" i gotovo.
Sad svi znaju sve. I svi idu kući isti dan.
Drugo rjesenje bi bilo da ih Janko sve snimi svojom kamerom visoke rezolucije, pa zatim taj snimak pusti na obliznjem projektoru, tako da svi mogu da vide sebe i boju svojih ociju, pa opet svi idu prvo vece.
Ili da njih 201 prebiju kapetana broda koji pristaje svako vece, pa svi fino zapale kuci...
Ili da...
I tako mozemo unedogled...
Promasio si poentu zadatka. Kao sto sam vise puta naglasio, radi se o cisto logickom razmisljanju ostrvljana (a to rjesenje smo i objasnili u prethodnim porukama), i nisu u pitanju nikakvi trikovi ili igra rjecima u postavci zadatka. (A ako ce vec ostrvljani da pricaju, kao sto rade u tvom rjesenju, onda je rjesenje dosta jednostavnije i nema potreba za naocarima. P: "Koje su boje moje oci?" G: "Plave." P: "Hvala, dovidjenja."  ).
Citat: galet@world: Niko ne misli na Gurua. Kako će on saznati boju svojih očiju, ili će ostati trajno na ostrvu?
Guru i osobe sa zelenim ocima ostaju na ostrvu.
[Ovu poruku je menjao peka dana 26.02.2009. u 15:02 GMT+1][ galet@world @ 26.02.2009. 15:35 ] @
Prvo Janko nije uradio ništa što je u suprotnosti sa odredbama zadatka (izuzev za Gurua) Onaj ko prima naočare nije dobio informaciju o svojim očima - on i dalje ne zna kakve su mu oči. On samo vidi da Janko daje naočare plavima koje on ionako vidi. Svaki logičar shvata šta je Jankov cilj i kad Guru kaže da vidi plavu boju sve je svima jasno (osim Guruu). Svi su jednaki logičari i jednako bi postupili kao Janko i zato znaju šta Janko hoće. Drugo - u tvom zadatku stoji da svi žele da odu sa ostrva - zašto onda zeleni ostaju?
Treće - zašto pričaš uopštene fraze - kaži konkretno šta nije u redu u mom rešenju. To sam i u prethodnoj poruci tražio. Biću zahvalan.
[ Bojan Basic @ 26.02.2009. 18:36 ] @
Citat: galet@world:
Treće - zašto pričaš uopštene fraze - kaži konkretno šta nije u redu u mom rešenju.
Nisi dokazao kako Janko ima gde da kupi sunčane naočare. [ galet@world @ 26.02.2009. 20:12 ] @
Ja se izvinjavam, nešto sam u gužvi ovih dana, a vidim da ima puno prilaza koje bih natenane da izanaliziram. U svakom slučaju, stići će komentar za koji dan.
[ bata kg @ 26.02.2009. 22:35 ] @
U pravu si.
Zadatak po mom ukusu, a ne nekakva mutljavina od logicara i Gurua.
[ peka @ 26.02.2009. 23:43 ] @
Citat: galet@world: Prvo Janko nije uradio ništa što je u suprotnosti sa odredbama zadatka (izuzev za Gurua) Onaj ko prima naočare nije dobio informaciju o svojim očima - on i dalje ne zna kakve su mu oči. On samo vidi da Janko daje naočare plavima koje on ionako vidi. Svaki logičar shvata šta je Jankov cilj i kad Guru kaže da vidi plavu boju sve je svima jasno (osim Guruu). Svi su jednaki logičari i jednako bi postupili kao Janko i zato znaju šta Janko hoće. Drugo - u tvom zadatku stoji da svi žele da odu sa ostrva - zašto onda zeleni ostaju?
Treće - zašto pričaš uopštene fraze - kaži konkretno šta nije u redu u mom rešenju. To sam i u prethodnoj poruci tražio. Biću zahvalan.
Pazi, formulisati zadatak tako da je jedino rjesenje ono u kom ostrvljani logickim putem zakljucuju boju svojih ociju (ono koje je ovde navedeno) je jako tesko. Znaci, ja bi sad trebalo u postavci zadatak da navodim da nema komunikacije, nema koristenja raznih objekata, nema nagadjanja boje ociju, nema ovog, onog, a to mi ne pada na pamet da radim. Fino sam rekao da je u pitanju logicko zakljucivanje i to bi trebalo da je dovoljno (to bi trebalo i sam da skapiras s obzirom u kom podforumu se nalazi zadatak). Ako ti to ne stima, onda eto, neka ti bude to rjesenje sa naocarima, bravo.
Zadaci su postavljeni ovde radi razonode i izazova. Ne shvatam koja je poenta da "rijesis" zadatak na kvarno, nisi primoran da ga rjesavas. [ galet@world @ 27.02.2009. 06:12 ] @
Ma jasno je meni rešenje. To sam i pokazao prilogom uz poruku od 22. 2. u 18:50, a sad saznajem da to nisam morao
da učinim jer nisam ni bio "primoran".
Poenta "kvarnog" rešenja je u tome da je ono moguće prema uslovima zadatka, a ni tebe niko ne tera da postavljaš
nedovoljno definisane zadatke.
Nego pređi na rešavanje konstrukcije trougla, ne primoravam te - od volje ti je.
[ Bojan Basic @ 27.02.2009. 12:03 ] @
Citat: galet@world:
Poenta "kvarnog" rešenja je u tome da je ono moguće prema uslovima zadatka, a ni tebe niko ne tera da postavljaš
nedovoljno definisane zadatke.
Moguće je, ali nije tačno (ili nije kompletno, ako tako više voliš; u svakom slučaju je matematički neprihvatljivo, jer nisu dokazane sve korišćene pretpostavke).  Prema tome, tvoja tvrdnja da je zadatak nedovoljno definisan ne opstaje. [ galet@world @ 27.02.2009. 13:39 ] @
Pa dobro - ja sam i tražio da me ispravite ako grešim. Ali konkretno.
Potpuno mi je jasno Kecmanovo rešenje, ali učinilo mi se da može i drukčije, pa pitam za to "drukčije":
U čemu je odstupanje od uslova zadatka?
Koje pretpostavke treba dokazati?
Zašto zeleni ostaju na ostrvu?
Ako mi se učinilo da može i drukčije, pa se pokaže da ne može - zašto bi neko takav pokušaj nazivao kvarnim?
Valjda bi bilo korektno lepo pokazati gde je greška. Unapred zahvalan.
[ Bojan Basic @ 27.02.2009. 17:13 ] @
Citat: galet@world:
U čemu je odstupanje od uslova zadatka?
Koje pretpostavke treba dokazati?
Odstupanje od uslova je u tome što se među uslovima nigde ne pominje da se na ostrvu nalazi prodavnica sunčanih naočara. Dakle, napravio si tu pretpostavku, pa je moraš i dokazati kako bi se tvoje rešenje moglo prihvatiti. [ peka @ 27.02.2009. 17:26 ] @
Evo ja cu samo jos ovo da napisem pa odustajem od rasprave, posto smo otisli u offtopic.
Rekao sam da se u zadatku radi o cisto logickom razmisljanju i namijenjen je ljudima koji vole da rjesavaju takve zadatke. Ako ti hoces da ga rijesis na neki drugi nacin, slobodno izvoli, ali mene takva rjesenja ne interesuju niti imam namjeru da uvodim pravila u zadatku koja eliminisu takva rjesenja. Dakle, mozes da smatras da je svako rjesenje koje se zasniva na nekakvoj "lukavosti" (a ima ih koliko hoces) potpuno tacno, ako ti to predstavlja neku satisfakciju. Go nuts.
I pored toga, tvoje rjesenje je netacno iz vise razloga:
1. Odakle im naocare na ostrvu?
2. Fino pise u zadatku da Guru kaze to sto kaze pred svima i od tada pocinje rjesavanje zadataka. Znaci, nema nikakvog pripremanja prije njegove izjave (stavljanja naocara), jer je to sad neki drugi zadatak, i nema veze sa ovim.
3. "a zauzvrat Janko kaže "Ja vidim smeđu boju"" Jesi ti uopste procitao zadatak? Nema komunikacije, osim onog sto je Guru rekao.
A sto se tice zelenih, opet, da si (pazljivije) procitao zadatak, vidio bi da sa ostrva ide svako ko sazna boju svojih ociju. Posto zeleni ne mogu da saznaju boju svojih ociju, oni ostaju, i tu je kraj price. (Ne mogu da saznaju logickim putem. Opet, rjesenja pomocu "trikova" su nesto drugo.) Uostalom, sto si toliko zapeo za njih, kao da ti ih je zao ili nesto. Zadatak nije "Naci nacin da svi odu sa ostrva", nego "Ko ide i kada?".
[ galet@world @ 27.02.2009. 18:57 ] @
Bojane ne misliš valjda ozbiljno - Janko se dogovorio s kapetanom broda, koji svake noći dolazi, da mu donese, naravno za lovu, 99 naočara.
Dakle, tu nije greška. Na drugom je mestu.
Peka je dao odgovor zašto Guru i zeleni ne idu s ostrva, ali ne znam zašto se Peka ljuti.
Gde je greška?
[ Nothingman @ 27.02.2009. 21:23 ] @
Kako znas da Janko ima lovu za cvike?
[ galet@world @ 27.02.2009. 21:49 ] @
Pa razmisli malo - da nije imao love ne bi ih mogao kupiti.
[ zzzz @ 28.02.2009. 00:35 ] @
Dane kaže:A sad evo jednog zadatka koji je zadavan na raznim forumima pa i ovde negde, ali ga niko nije uspeo da reši.
Zadat je prav ugao, dužina hipotenuze i položaj neke tačke kroz koju ta hipotenuza treba da prođe.
Treba konstruisati trougao.
To se može riješiti na više načina bez većih problema.Važno nam je naći
tačke na krakovima pravog ugla gdje hipotenuza počinje i završava.
To možemo naći naprimjer algebarski koristeći pitagorino pravilo i omjer
stranica sličnih trouglova (pravouglih).
Možemo i pomoću A-CAD-a u par poteza sa dovoljnom tačnošću.
Možemo i pomoću šestara, lenjira i olovke koristeći pravila centralnog,
i perifernog ugla u kružnici sa još par dodataka kako bi se sve tačke
poklopile.
Ali nećemo ništa od toga.Što bi se patili kad možemo sve riješiti pomoću
plavih naočara.Pustimo da hipotenuza dužine l klizi preko tačke M sve
dok joj krajevi ne legnu na krakove pravog ugla.Posmatrajući kroz plave
naočari možemo tačno utvrditi pravi položaj hipotenuze pod uslovom
da je i ona plava.
Evo kako sam ja to riješio.Ako nije tačno recite zašto nije.
[ galet@world @ 28.02.2009. 04:46 ] @
I ovde rešenje sa naočarima sadrži grešku. Treba naći grešku i tamo i ovde.
Ovde je to lako, greška je u boji naočara - ne treba koristiti plave već potpuno neprozirne - protiv stresa.
Pričam ti priču - može ovako, može onako, ali umesto trougla i šestara koristi se alat: bla, bla, bla.
[ peka @ 28.02.2009. 22:22 ] @
Citat: galet@world: Pa razmisli malo - da nije imao love ne bi ih mogao kupiti.
Mislim da ti treba malo da razmislis. [ bata kg @ 28.02.2009. 22:44 ] @
Moram da priznam da mi se dopalo ono.....bla, bla, bla....
Mislim da sam resio zadatak.....ispada da se svodi na konstrukciju paralelograma.
Ako treba tu je i celo resenje, mislim, da ne kvarim zadovoljstvo pre svega zzzz pa ni ostalima.
.
.
.
ako imate jos neki neresen zadatak samo napred, nesta mi mnogo dobro idu
( a i od skoro sam ovde kao sto znate)
[ Ecrabera @ 07.04.2009. 21:17 ] @
Dve osobe treba da se nađu na nekom mestu između 9h i 10h. Dogovorile su se da svaka dođe bilo kad između 9h i 10h, čeka 20min, a zatim odlazi ako se druga osoba nije pojavila. Naći verovatnoću da će se ove dve osobe sresti. :P
[ mayobayo @ 10.04.2009. 18:24 ] @
8/9?
[ holononi @ 12.04.2009. 23:28 ] @
Citat: Dve osobe treba da se nađu na nekom mestu između 9h i 10h. Dogovorile su se da svaka dođe bilo kad između 9h i 10h, čeka 20min, a zatim odlazi ako se druga osoba nije pojavila. Naći verovatnoću da će se ove dve osobe sresti.
X – vreme kada stiže osoba A
Y – vreme kada stiže osoba B
X ima uniformnu raspodelu sa parametrima 9 i 10
Y takodje ima uniformnu raspodelu sa parametrima 9 i 10
Povoljno je |X – Y| < 1/3 (to jest 20 minuta).
Ovo je primer primene geometrijske definicije verovatnoće. Skup svih ishoda je
Ω = {(x, y) iz R^2: 9 ≤ x ≤ 10, 9 ≤ y ≤ 10 }
A = {(x, y) iz Ω: |x – y| < 1/3 } - povoljni ishodi.

p = m(A) / m(Ω) = ((1*1) – (2/3)^2) / (1 * 1) = 5/9
[ mayobayo @ 13.04.2009. 10:50 ] @
pa da..
(povrsina kvadrata - povrsine trouglica)/povrsina kvadrata = 5/9
kako li ja dobih 8/9 heheheh
[ ptak 13. @ 25.04.2009. 00:29 ] @
E evo opet mene, posle duzeg vremena prikupio sam dvadesetak zadataka (logickih) pa da postavim sad jedan.....aj probajte resiti
Nastavite niz: 71, 78, 79, 20, 27…
Teško da vam ovde može pomoći preterano matematičko mozganje ali probajte.
Lako je samo se trebate setiti sta je zajednicko za brojeve u nizu ! ! !
[ Farenhajt @ 25.04.2009. 01:48 ] @
Citat: ptak 13.: E evo opet mene, posle duzeg vremena prikupio sam dvadesetak zadataka (logickih) pa da postavim sad jedan.....aj probajte resiti
Nastavite niz: 71, 78, 79, 20, 27…
Teško da vam ovde može pomoći preterano matematičko mozganje ali probajte.
Lako je samo se trebate setiti sta je zajednicko za brojeve u nizu ! ! !
Da li je odgovor 21? [ Tea94 @ 25.04.2009. 09:05 ] @
71, 78, 79, 20, 27...
da nije mozda 28?
[ holononi @ 25.04.2009. 10:04 ] @
Citat: Nastavite niz: 71, 78, 79, 20, 27…
(Jedno rešenje)
Prva cifra prva tri člana je ista pa je za sledeća tri člana takodje ista tj 2.
Druga cifra trećeg člana se dobije tako da se druga cifra prethodna dva člana sabere, pa je druga cifra šestog člana 7.
Dakla rrešenje je 27.
[ holononi @ 25.04.2009. 10:17 ] @
Citat: Nastavite niz: 71, 78, 79, 20, 27…
A evo i ostalih rešenja
Ako se rešenje traži u skupu celih brojeva, Z, polinom
Pn(x) = (x - 71)(x - 78)(x - 79)(x - 20)(x - 27)(x - n)
se anulira sa svako n iz Z, pa je rešenje svako n iz Z.
[ ptak 13. @ 25.04.2009. 10:53 ] @
Ne nijedno od tih resenja nije resenje ovog zadatka....zadatak je logicki i ne treba resenje traziti u matematici.....
Jedina stvar ovde je da je onaj ko je pisao niz pisao tako da je za njega broj 1 ustvari broj 7 a broj 7 ustvari broj 1
Niz je 71, 78, 79, 20, 27…
A resenje je
17, 18, 19, 20, 21
Da li razumete....?!  Umesto jedinice pise 7 i umesto sedmice pise 1 . 
Evo novog zadatka !
Otac je pozvao ćerku I zamolio je da mu kupi neke stvari neophodne za put. Rekao joj je da se novac nalazi u koverti na stolu. Devojka je na tren pogledala koverat, videla da na njemu piše 98, uzela novac, I ne brojeći stavila ga u novčanik I otišla.
U prodavnici je kupila stvari za 90 dinara a kada je htela da plati, ispostavilo se da umesto da joj je ostalo 8 dinara da joj fali 4. Kad je došla kući upitala je oca da nije on pogrešio kada je brojao pare. Otac je odgovorio da je on izbrojao tačno ali da je ona pogrešila. Gde je greška?
Ovaj sa cerkom i ocem je bas lak, samo razmisljate o koverti ! [ X Files @ 25.04.2009. 11:04 ] @
86 <---> 98
?
[ ptak 13. @ 25.04.2009. 12:47 ] @
Tako je  bravo
Evo jos jedan ....
Ja nemam džepni sat, samo zidni koji je stao. Pošao sam kod svog prijatelja da vidim koliko je sati. Video sam I ne zadržavši se dugo vratio sam se kući. Kući sam izveo ne složeni račun I doterao svoj sat Ida pokazuje tačno vreme.
Šta sam ja uradio I kako sam rasuđivao ako nisam znao koliko vremena mi je prošlo u putu?
[ Bojan Basic @ 25.04.2009. 13:03 ] @
Zaboravio si napomenuti da si pre posete prijatelju pokrenuo sat (s kakvim god vremenom na njemu).
[ holononi @ 25.04.2009. 13:24 ] @
Citat: ne treba resenje traziti u matematici.....
Oooppsss, mi smo ovde zapenili na matematiku. Da nisi pogrešio forum?
[ ptak 13. @ 25.04.2009. 13:40 ] @
Citat: Bojan Basic: Zaboravio si napomenuti da si pre posete prijatelju pokrenuo sat (s kakvim god vremenom na njemu).
Da, to je u stvari resenje 
Citat: holononi: Oooppsss, mi smo ovde zapenili na matematiku. Da nisi pogrešio forum?
Pa mislim da nisam, jer sam i pre postovao slicne zadatke koji se resavaju zdravom logikom i razmisljanjem a ne matematickim putem....stoga mislim da nisam...a ti, mislis da jesam ?!   [ holononi @ 25.04.2009. 15:37 ] @
Citat: jer sam i pre postovao slicne zadatke koji se resavaju zdravom logikom i razmisljanjem a ne matematickim putem....
Pošto je ovo forum Matematika, takvi treba da budu i zadaci. Medjutim zadatak sa nizom kako si ga ti postavio nije u duhu matematičkih pravila. U postavci zadatka si trebao da navedeš definiciju ili dokažeš tvrdjenje da je 1==7 ili nešto tako ako insistiraš da dobiješ odgovor kakav tražiš. U suprotnom tačnih odgovora ima najmanje beskonačno. Na primer ako je 2 zamena za 8 onda je sledeći član 88. Ili ako je 71 zamena za L, 78 zamena za O, 79 zamena za P, 20 zamena za A, 27 zamena za T onda je sledeći član 20. Takodje, kad je u pitanju zadatak 86 <-> 98 imamo da je neko nešto pogrešio. U matematici se ne priznaju zadaci kad neko nešto pogreši.
Naravno, na času matematike je zgodno ispričati anegdotu da bi se održala pažnja. Pa u tom smislu nije loše ubaciti i neki takav zadatak pod uslovom da se ne preteruje.
Da ne otvaram još jedan post evo jednog lakog baš matematičkog zadatka. Izvinjavam se ako se već pojavio negde na forumu.
Za n iz skupa celih brojeva, da li 7 | (n^7 - n) ??? Naravno uz odgovarajući dokaz. [ Farenhajt @ 25.04.2009. 16:30 ] @
Citat: holononi: Da ne otvaram još jedan post evo jednog lakog baš matematičkog zadatka. Izvinjavam se ako se već pojavio negde na forumu.
Za n iz skupa celih brojeva, da li 7 | (n^7 - n) ??? Naravno uz odgovarajući dokaz. 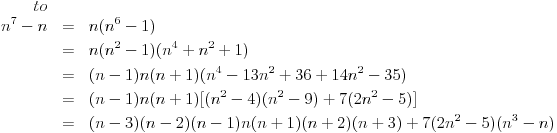
Pošto je proizvod sedam uzastopnih celih brojeva deljiv sa sedam, zaključak sledi. [ holononi @ 25.04.2009. 18:25 ] @
@Farenhajt
Lepo, brzo i korektno.
Da li neko ima drugačiji dokaz 7|(n^7 - n), n iz Z.?
-------------
Istina je jedna, samo su putevi do nje različiti.
[ Farenhajt @ 25.04.2009. 19:42 ] @
Citat: holononi: @Farenhajt
Lepo, brzo i korektno.
Da li neko ima drugačiji dokaz 7|(n^7 - n), n iz Z.?
-------------
Istina je jedna, samo su putevi do nje različiti.
Možemo dati kratak dokaz Fermaove male teoreme:
Ako je  prost broj, onda 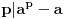 za svaki ceo broj  .
Dokaz: ako 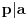 , dokaz je nepotreban. Stoga 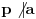 , pa moramo dokazati 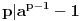 .
U tom cilju, posmatrajmo brojeve  . Nijedan od njih nije deljiv sa  . Pretpostavimo da neka dva među njima daju isti ostatak pri deljenju sa  - recimo 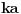 i 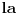 . Tada je 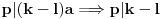 . Međutim, 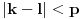 , pa je to moguće samo ako 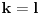 .
Prema tome, tih 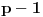 brojeva daju 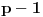 različitih nenultih ostataka pri deljenju sa  , pa imamo
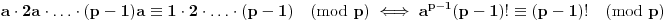
To nam daje 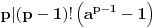 , ali pošto prvi činilac nije deljiv sa  , zaključujemo da 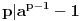 .
[Ovu poruku je menjao Farenhajt dana 25.04.2009. u 23:08 GMT+1][ holononi @ 25.04.2009. 21:10 ] @
Naravno, a pošto se Fermaova mala teorema može dokazati indukcijom onda ne moram ni da pitam da li postoji treći dokaz.
Postavio sam ovo pitanje jer sam na jednom matematičkom forumu pronašao suprotan dokaz, pa me je zanimalo da li smo i mi tako "spretni". Nažalost, nisam sačuvao adresu tog foruma.
[ galet@world @ 04.06.2009. 22:37 ] @
Ovaj zadatak sam ja izmislio, pa možda i nije nešto naročito:
Podeli neki raznostrani trougao na proizvoljan broj jednakih delova izlomljenom linijom u jednom potezu.
[ zzzz @ 05.06.2009. 00:20 ] @
Ja sam podijelio na dvoje.Šta sad dalje?Treba li na troje itd?
[ holononi @ 05.06.2009. 00:24 ] @
To je dovoljno za paran broj delova. Hajde sad za neparan.
[ Nedeljko @ 05.06.2009. 06:36 ] @
Galet, a šta smatraš pod jednakim delovima, delove koji imaju jednake površine ili delove koji su podudarni, to jest osim površine imaju i isti oblik? Ako je ovo drugo u pitanju, baš bih voleo da vidim rešenje. Ako si to uspeo, svaka ti čast. Jednakost površina nije teško ostvariti.
[ galet@world @ 05.06.2009. 07:18 ] @
Citat: Nedeljko: Galet, a šta smatraš pod jednakim delovima,....
Jedan te isti deo ponovljen više puta.
Milane, izjave ne važe kao rešenje - treba i da se pokaže (nacrta).
NAPOMENA:
"Proizvoljan broj" ne znači svaki broj, ali ako neko zna i za svaki broj - nemam ništa protiv.
Proizvoljan broj, dakle, znači svaki broj za koji je to moguće učiniti.
(naravno, radi se o celim brojevima)
Raznostraničan trougao znači baš svaki. [ Nedeljko @ 05.06.2009. 07:31 ] @
U tom slučaju, iskreno me mrzi da rešavam, ali jedva čekam da vidim rešenje.
[ galet@world @ 05.06.2009. 08:16 ] @
Koliko dugo možeš da čekaš?
Ili da odredimo neki pristojan rok.
[ holononi @ 05.06.2009. 08:57 ] @
Ako je trougao ABC, povuče se duž iz temena A do preseka sa stranicom BC, u tački D1, tako da površina trougla ACD1 bude n-ti deo površine trougla ABC. Zatim se nastavi iz tačke D1 u tačku D2 koja je na stranici AB tako da površina trougla AD1D2 bude n-ti deo površine trougla ABC. Tačka D3 je opet na stranici BC, a trougao je D1D2D3. I tako redom do poslednjeg trougla Dn-2Dn-1B.
Površinu polaznog trougla ABC nije teško odrediti pa ni površinu n-tog dela. Polazni trougao je ABC, deli se na n-delova i kad se odredi tačka D1, imam isti problem ali sada sa trouglom AD1B koji treba podeliti na n-1 delova.
Ako je trougao dat koordinatama tačaka A, B i C, koristim poznate obrazace za izračunavanje površine trougla datog koordinatama temena, a ako nije prevedem ono što je dato u neki koordinatni sistem pa opet imam tri tačke. Znači problem je rešiv i u tri dimenzije. Radi lakšeg računa, transformišem koordinate tako da tačka A bude u koordinatnom početku. Odredjujem koordinate tačke D1 numerički, na primer metodom polovljenja stranice BC. Koristim formulu datu pod (2).
(1)
Dodelim B0 = B, C0 = C.
(2)
D1( (xB0 + xC0)/2, (yB0 + yC0)/2, (zB0 + zC0)/2 )
(3)
Izračunam površinu trougla AD1C
(4)
Ako je površina trougla AD1C jednaka n-tom delu površine trougla ABC, korak (7).
(5)
Ako je površina trougla AD1C veća od n-tog dela površine trougla ABC, zamenim tačku B0 sa tačkom D1 i vraćam se na korak (2).
(6)
Zamenim tačku C0 sa tačkom D1 i vraćam se na korak (2).
(7)
Rezulat su koordinate tačke D1. Kraj!
Sldeeće je da podelim trougao AD1B na n-1 delova, itd.
[ galet@world @ 05.06.2009. 09:32 ] @
Ali šta je sa "izlomljenom linijom u jednom potezu"?
Za rešenje ovog zadatka ne treba biti matematičar - samo treba nacrtati neki trougao podeljen
tom izlomljenom linijom na, recimo, 100 jednakih delova.
I ne samo to već i trougao koga delimo na jednake delove i svi jednaki delovi mogu se nacrtati u
jednom potezu.
P.S.
Nisam ulazio u detalje tvog rešenja, ali površno gledajući ti si zanemario Nedeljkovo pitanje jer
n-ti delovi velikog trougla moraju biti potpuno isti, a ne samo po površinama.
[Ovu poruku je menjao galet@world dana 05.06.2009. u 10:51 GMT+1]
[ Nedeljko @ 05.06.2009. 10:33 ] @
Ta izlomljena linija je trougao koji spaja središta stranica datog trougla, malopre mi je palo na pamet. Nije loša caka. Na sličan način se trougao može podeliti na 4n podudarnih trouglova.
[ holononi @ 05.06.2009. 12:58 ] @
Citat: Nisam ulazio u detalje
Ko ne ulazi u detalje ne treba ni da postavlja pitanja.
Citat: proizvoljan broj jednakih delova izlomljenom linijom u jednom potezu
Moje rešenje zadovoljava dati uslov. Otvorena poligonlna linija data tačkama {A, D 1, D 2, D n-1}, je rešenje zadatka.
Naravno, pri računnju treba uzeti u obzir odredjenu tačnost za neko unapred izabrano  .
[ Nedeljko @ 05.06.2009. 13:56 ] @
Kakvo sad  , kada delovi moraju biti podudarni? Koliko sam shvatio tvoju konstrukciju, za n=2 ćeš trougao ABC podeliti težišnom linijom na dva trougla, ali oni nisu podudarni.
 [ holononi @ 05.06.2009. 14:30 ] @
Citat: Podeli neki raznostrani trougao na proizvoljan broj jednakih delova izlomljenom linijom u jednom potezu
Gde se ovde pominje podudarnost? Govori se o "jednakim delovima". U tom smislu zadatak je rešen opisanim algoritmom.
Citat: Kakvo sad 
Udubi se malo u rešenje pa ćeš videti gde je potreban taj epsilon.
Ako sada preciziramo zadatak da dobijemo podudarne trouglove, razmotriću i to pitanje, ako razmotrim. Samo nemojte posle reći, hteli smo da to budu kvadrati.
Poniudite neko rešenje.
Citat: podeliti na 4n podudarnih trouglova.
Malom modifikacijom algoritma koji sam opisao lako se može dobiti 2 n trouglova povlačenjem duži kroz težišne linije. U principu treba izbaciti korake (4) - (6). Nakon što se ispolovi jedna polovina trougla, ponoviti postupak za drugu polovinu itd. Elementarna rekurzija.
[ Bojan Basic @ 05.06.2009. 14:39 ] @
Citat: holononi:
Gde se ovde pominje podudarnost?
Evo ovde:
Citat: galet@world: Jedan te isti deo ponovljen više puta.
I ovde:
Citat: galet@world:
n-ti delovi velikog trougla moraju biti potpuno isti, a ne samo po površinama. [ holononi @ 05.06.2009. 14:57 ] @
To su naknadne intervencija a ja sam rešavao originalni zadatak. Naravno, nemam ništa protiv da sad imamo novi ili korigovan zadatak. Ali namerno insistiram na polaznom zadatku, jer ovde ima ljudi koji će danas-sutra, ako ne i juče, zadavati zadatke učenicima i zato pre nego što postave pitanje moraju pažljivo da razmotre šta očekuju i da li pitanje zaista upućuje na jedinstven odgovor.
Zašto sam tako "zadrt"? Zato šo mi se dešavalo na pismenom da asistent nekima da naknadna objašnjenja a nekima ne da. Zadatak se ispostavi da nije moguće rešiti bez tih dodatnih intervencija i oni koji su rešili sa intervencijom su u povoljnijem položaju od onih koji nisu. Za takve "nestašluke" nemam opravdanja. Zadatak se ili odbacuje ili se usvaja kao da su svi rešili. U stvari treba ovo drugo, jer je povoljnije za studenta, koji je utrošio trud i vreme na zadatak bez obzira što ga nije rešio.
[ Nedeljko @ 05.06.2009. 16:17 ] @
Citat: holononi: Udubi se malo u rešenje pa ćeš videti gde je potreban taj epsilon.
Ako je epsilon potreban, onda to nije rešenje zadatka u kome se traži tačna dekompozicija lika na n jednakih delova. [ holononi @ 05.06.2009. 17:30 ] @
Potpuno se slažem jer je reč o numeričkom a ne analitičkom rešenju. Pa ako se insistira na analitičkom rešenju izvolite prezentirajte.
[ galet@world @ 05.06.2009. 17:57 ] @
Citat: holononi:Moje rešenje zadovoljava dati uslov.
Ne zadovoljava.
Gde u originalnom zadatku stoji da ti delovi treba da budu jednaki samo po površinama?
Ako se kaže da delovi treba da budu jednaki, a ne kaže se po čemu, onda to znači da ti delovi treba da
budu jednaki po svemu.
Blizanci su u principu jednaki, a ne osobe koje imaju samo isti broj kilograma.
Tvoji trouglovi {A, D1, D2, Dn-1}, nisu jednaki ni po dužini stranica ni po uglovima
Citat: Nedeljko: Ta izlomljena linija je trougao koji spaja središta stranica datog trougla, malopre mi je palo na pamet. Nije loša caka. Na sličan način se trougao može podeliti na 4 n podudarnih trouglova.
Ovo 4 n jeste rešenje ali delimično jer preskače mnoga rešenja između, ali sad sam video
da umeš i da crtaš - pa nactraj to jer mora biti u jednom potezu, ali i da se vidi kako.
[ holononi @ 05.06.2009. 18:32 ] @
Citat: Ako se kaže da delovi treba da budu jednaki, a ne kaže se po čemu, onda to znači da ti delovi treba da budu jednaki po svemu.
A da li će ti delovi biti "jednaki po svemu", na primer po rastojanju od koordinatnog početka? Ili po orjentaciji u prostoru? Da li će im strane zauzimati isti ugao u odnosu na stranicu trougla AB? Itd, itb. [ galet@world @ 05.06.2009. 18:58 ] @
Zaboravio si još da dodaš boju, miris, okus i mnoge druge stvari koje ne spadaju u definiciju nekog
geometrijskog lika.
[ holononi @ 05.06.2009. 20:16 ] @
U ovom slučaju govorim samo u terminima geometrijskih pojmova.
Evo još jednog rešenja, ali samo kao napomena jer se pominje faktor 4n.
Fraktali Hausdorff-ove dimenzije log(3)/log(2) ili 1 + log(3)/log(2) ili 1+ log(3)/log(5) itd, poznti kao trouglovi Sierpinski, daju neka rešenja za ovaj zadatak. Algoritama i programskih rešenja ima i u našoj literaturi pa nema potrebe da se ponavljam. Samo ću da napomenem da se može opet poći od simetrala stranica i prvo rešenje je spajanje simetrala stranica koje se odredjuju formulom, na primer za stranicu BC
as( (xB + xC)/2, (yB + yC)/2, (zB + zC)/2 )
za ostale stranice slično. Dobije se podela na 4 podudarna trougla koji se dalje dele svaki na još četiri itd. Prema tome, opet rekurzija. Primere imate u knjigama
D. Urošević, "Algoritmi u programskom jeziki C", Mikro knjiga, Beogrd, 1996.
N. Wirth, "Programiranje na jeziku Modula-2", Mikro knjiga, Beograd, 1990.
N. Wirth, "Algoritmi i strukture podataka", Mir, Moskva, 1989. (na ruskom)
Tu takodje imate i crtanje Hilbertovih kriva.
[ Cabo @ 05.06.2009. 20:22 ] @
Citat: galet@world: Zaboravio si još da dodaš boju, miris, okus i mnoge druge stvari koje ne spadaju u definiciju nekog
geometrijskog lika.
Zaboravio si na geometriju Lobačevskog. U njoj je zbir uglova u trouglu strogo manji od  . [ galet@world @ 05.06.2009. 22:30 ] @
Pa čemu priča? Nacrtajte to što se traži!
[ holononi @ 05.06.2009. 22:52 ] @
Saveti i sugestije su besplatni, ali izradu programa naplaćujem.
[ galet@world @ 05.06.2009. 23:38 ] @
Izgleda da nemaš šta da naplatiš.
[ Nedeljko @ 06.06.2009. 08:34 ] @
Citat: holononi: Fraktali Hausdorff-ove dimenzije log(3)/log(2) ili 1 + log(3)/log(2) ili 1+ log(3)/log(5) itd, poznti kao trouglovi Sierpinski, daju neka rešenja za ovaj zadatak. Algoritama i programskih rešenja ima i u našoj literaturi pa nema potrebe da se ponavljam. Samo ću da napomenem da se može opet poći od simetrala stranica i prvo rešenje je spajanje simetrala stranica koje se odredjuju formulom, na primer za stranicu BC
a s( (x B + x C)/2, (y B + y C)/2, (z B + z C)/2 )
za ostale stranice slično. Dobije se podela na 4 podudarna trougla koji se dalje dele svaki na još četiri itd. Prema tome, opet rekurzija.
Koliko znam, na opisani način će ti srednji trougao ostati nepopunjen. Za ovo ti treba fraktal dimenzije 2, što onda i nije više fraktal, ali nije bitno je mislim na odgovarajuće rekurzivne konstrukcije. U svakom slučaju, ne može sa fraktalima dimenzije ispod 2.
Ono što sam predložio jeste rešenje do na zahtev za dokazom mogućnosti da se to nacrta u jednom potezu, kao što je Galet primetio. No, to se može rešiti primenom Ojlerove teoreme (koju je Hirholcer dokazao) o tome koji se grafovi mogu nacrtati jednom potezu, a koji ne.
http://en.wikipedia.org/wiki/Euler_path
No, nisam eksplicitno konstruisao rešenje u jednom potezu, pa ne bi bilo loše da se to učini. [ galet@world @ 06.06.2009. 09:06 ] @
Predlažem da još malo sačekamo.
[ holononi @ 06.06.2009. 10:06 ] @
Citat: Koliko znam, na opisani način će ti srednji trougao ostati nepopunjen.
Biće popunjen samo treba biti pažljiv sa rekurzijom. Nije teško. U stvari postoji rešenje za svako p iz N, p > 1. Moguće je kontruisati p 2n podudarnih trouglova. Sad žurim na pijacu pa kad se vratim daću neke detalje. [ galet@world @ 06.06.2009. 10:45 ] @
E ovo me već nervira pa moram nešto da kažem. Svaki trougao na ovaj način može se
podeliti na n2 delova gde je n bilo koji ceo broj
[ Nedeljko @ 06.06.2009. 12:05 ] @
Da, tako je. Na sasvim sličan način može na n 2 delova, gde je n bilo koji prirodan broj. Potpuno sam smetnuo sa uma da konstrukciju uopštim na sasvim elementaran način.
Citat: holononi: Biće popunjen samo treba biti pažljiv sa rekurzijom. Nije teško.
Ako rešiš taj problem, dimenzija će biti 2, a ne manja od 2. [ holononi @ 06.06.2009. 13:01 ] @
Na slici je primer za p = 3, n = 1.
Dajem opštu formulu za podelu stranice trougla u r-dimenzionom prostoru, r > 1:
a h( (x 11 + x 12)/h, (x 21 + x 22)/h, ..., (x r1 + x r2)/h )
gde je h = p, p-1, ..., 2.
Na primer, stranica AB je data koordinatama tačaka
A( x 1A, x 2A, ..., x rA )
B( x 1B, x 2B, ..., x rB ).
 [Ovu poruku je menjao holononi dana 06.06.2009. u 14:27 GMT+1]
[Ovu poruku je menjao holononi dana 06.06.2009. u 14:27 GMT+1][ galet@world @ 06.06.2009. 14:36 ] @
Tako je. Bravo! Samo ne znam zašto to odmah nisi uradio.
P.S.
Smatram da je ovom rešenju mnogo doprineo Nedeljko
Evo može i ovako:
[Ovu poruku je menjao galet@world dana 06.06.2009. u 16:04 GMT+1]
[ holononi @ 06.06.2009. 15:10 ] @
Citat: zašto to odmah nisi uradio
Iz prostog razloga što smo morali da preciziramo zadatak. Ispisao sam rešenje koje mi je prvo palo na um jer uglavnom imam zadatke u kojima se mora odrediti površina kao mera neke pojave, zato prvo rešenje. Jednakost trouglova je širok pojam, dok je podudarnost trouglova tačno definisana [ galet@world @ 06.06.2009. 17:10 ] @
Zadatak je rešen mada ja nisam mislio da će ispasti toliko interesantan, međutim, ovo mi nekako ne ide
"pod kapu":Jednakost trouglova je širok pojam
Ako kažeš nekom da su dve ili više stvari jednake onda se valjda podrazumeva potpuna jednakost.
Ti si uzeo kao kriterijum jednakosti jednake površine, ali ne po obliku površina nego po količini.
Neko je mogao za kriterijum jednakosti uzeti obim delova , a neko je mogao uzeti uglove.
Smatram da je izraz "jednaki delovi" potpuno jasan i ne može se tumačiti na više načina.
Tvoje mišljenje po ovom pitanju sam saznao, ali me intersuje i mišljenje ostalih učesnika.
[ holononi @ 06.06.2009. 17:34 ] @
Trouglovi mogu biti jednaki po boji, veličini itd, dok je podudarnost pojam koji se koristi u matematici sa tačno odredjenim značenjem.
Jeste, @Nedeljko je doprineo negirajući moje stavove. I to je doprinos.
Citat: @Nedeljko: Koliko znam, na opisani način će ti srednji trougao ostati nepopunjen. Citat: holononi: Biće popunjen samo treba biti pažljiv sa rekurzijom. Nije teško. Citat: @Nedeljko: Ako rešiš taj problem, dimenzija će biti 2, a ne manja od 2.
Svi ste vi to znali samo ste mene proveravali.
[Ovu poruku je menjao holononi dana 06.06.2009. u 18:47 GMT+1][ Nedeljko @ 06.06.2009. 21:34 ] @
Citat: holononi: Jeste, @Nedeljko je doprineo negirajući moje stavove. I to je doprinos.
Svi ste vi to znali samo ste mene proveravali.
Šta smo znali? Gde je najavljena rekurzija? Ja sam rekao da ako rešiš problem sa rekurzijom, onda će dimenzija biti 2. Daleko od toga da sam proveravao da li je takvo fraktalno rešenje moguće. Što se mog doprinosa tiče, zaboravio si da sam ja podelio trougao na jednake delove.
@Galet
Zadatak jeste (barem meni) interesantan i čestitam ti ako si autor. Jesi li? [ galet@world @ 06.06.2009. 22:59 ] @
Jesam. Nešto sam muvao oko onog zadatka koji je Bojan rešio (da se trougao podeli na dve jednake površine najkraćom linijom)
i nacrtao sam jedan jednakostraničan trougao pa u njemu jedan manji i dobio sam četiri jednaka manja. Onda sam to uradio za
jednakokraki trougao pa za raznostraničan. I onda sam hteo da nacrtam jedan veći trougao i da ga podelim na više delova, ali sam
odustao jer sam u već nacrtane manje trouglove ponovio postupak - jasno mi je bilo da se postupak može ponavljati u nedogled i
da je to fraktal, Ne mogu samo da se setim zašto sam došao na ideju da to uradim u jednom potezu - verovatno zato što mi se
svidela slika kad sam trougao podelio na devet delova, a to sam učinio u jednom potezu i dobio sam tri manja trougla u vidu
lista deteline, naravno, tu su bili i oni ostali trouglovi između listova deteline i u njihovom produžetku. E onda sam nastavio i odmah
sam otkrio da se to može uraditi i za one fraktalske trouglove i t. d. U početku sam samo delio zadani trougao, a onda sam video
da se i on i njegovi delovi mogu uraditi u jednom potezu. Eto - nije to bogzna šta, ali ispalo je interesantno.
[ galet@world @ 07.06.2009. 08:50 ] @
Citat: holononi: Trouglovi mogu biti jednaki po boji, .......... dok je podudarnost pojam koji se koristi u matematici sa tačno odredjenim značenjem. Opet ja. Očigledno je da sam vrlo tvrdoglav. Ako kažemo da su neke stvari jednake po nekim svojim karakteristikama,
ali ne svim - onda se mora naglasiti koje su to karakteristike. Čak i u slučaju kad su trouglovi podudarni - oni nisu
jednaki ako se razlikuju po boji. Znam da boja nije matematički pojam, ali jednakost jeste.
Prema tome izraz "jednako" u konkretnom slučaju je višeg stepena od izraza "podudarno"
Ako kažemo da su trouglovi jednaki, a ne kažemo po kojim karateristikama onda se mora podrazumevati da su
jednaki po svim karakteristikama t. j. mora se podrazumevati identičnost.
Ako me neko pita - a da li su jednaki po boji? - mogu s pravom da kažem - pa rekao sam da su jednaki - zar ne?
Upravo zato što se izraz "jednako" može i drukčije tumačiti nego ovako kako ja smatram i Nedeljko me pitao šta
podrazumevam pod tim izrazom
[ Nedeljko @ 07.06.2009. 10:34 ] @
Delimično ste obojica u pravu.
Jednakost A=B u matematici znači da su A i B upravo isti objekat, dakle, jedan objekat, a ne dva, što bi u slučaju trouglova značilo da su jednaki oni trouglovi koji imaju sva tri temena zajednička. Tu je holononi u pravu. Zato je i dao primedbu da jednakost po svemu znači i po rastojanju od koordinatnog početka itd.
Međutim, ponekad se u geometriji koristi izraz "jednako", koa zamena za "podudarno", što nije baš formalno korektno, ali se može reći ako se sagovornici razumeju. Stoga sam ja pitao na šta se misli i bilo je objašnjeno. Stoga holononi nije imao izgovor za netačna rešenja zadatka. No, istina je da je u ovom značenju formalno jedino ispravno koristiti izraz "podudarno".
Što se boja tiče, često se preslikavanje skupa A u skup B naziva bojenjem elemenata skupa A bojama iz skupa B.
[ holononi @ 07.06.2009. 10:58 ] @
Na skupu svih trouglova na svetu definišem relaciju jednakosti trouglova, ~, na sledeći način:
x ~ y <=> |AxBx| = 2|AyBy|
gde |.| označava dužinu strane trougla, pa su trouglovi jednaki ako i samo ako je dužina strane AB trougla x jednaka dvostrukoj dužini strane AB trougla y. Medjutim ovi trouglovi nisu podudarni.
U geometriji postoje aksiome podudarnosti i tu nema šta da se doda osima ako neko ne zna za to.
[ Nedeljko @ 07.06.2009. 13:57 ] @
Ma, u redu je, podudarnost je jasan i nedvosmislen pojam u geometriji, a jednakost se u matematici ne definiše u posebnim slučajevima, već postoji jedan univerzalan pojam jednakosti koji se primenjuje na sve. Zapravo, u standardnom zasnivanju matematike (predikatski račun prvog reda + ZFC teorija skupova) jedini objekti su skupovi, pa postoji samo jednakost skupova, odnosno, sve ostalo su posebni slučajevi.
Međutim, formalizam služi da bi bilo jasno šta se hoće, a u ovom slučaju je to bilo i razjašnjeno. Tvoj problem je što ne želiš da čitaš tuđe poruke. Daleko od toga da mislim da ne znaš šta je jednakost, a šta podudarnost i tu apsolutno nema nikakve potrebe da se pravdaš i dokazuješ.
[ holononi @ 07.06.2009. 16:22 ] @
Dva skupa su jednaka ako i samo ako su im elementi jednaki. Ako je trougao T1( (1, 1), (2, 1), (2, 2) ) a trougao T2( (-1, -1), (-2, -1), (-2, -2) ), tada su ovi trouglovi podudarni, ali nisu jednaki.
Neko je ovo davno primetio pa da bi izbegao kontradikcije jednakost je ostala jednakost a podudarnost je postala podudarnost.
Jednakost je ostala još samo u predškolskim bojankama odakle i potiče "originalnost" ovog zadatka. Zato je traženo
Citat: da se pokaže (nacrta). [ Nedeljko @ 07.06.2009. 16:42 ] @
Pa, dobro, jesi li ti smislio nešto originalnije?
[ galet@world @ 07.06.2009. 20:10 ] @
Citat: holononi: Ako je trougao T1( (1, 1), (2, 1), (2, 2) ) a trougao T2( (-1, -1), (-2, -1), (-2, -2) ), tada su ovi trouglovi podudarni, ali nisu jednaki.
Kako bilo da bilo, ali ovo je preterivanje. Ako ja odem u Novi Sad više nisam ono što sam bio u Beogradu - dobro stariji sam
nešto, ali ako trougao premestim na drugo mesto onda ispada da on više nije ono što je bio. Položaj trougla ili njegova
orijentacija nisu karakteristike trougla kao pojave. Položaj i orijentacija trougla su drukčiji u odnosu na druga mesta u ravni, ali
njegove("trouglovove") karakteristike nisu.
Ovaj citat gore čak znači da jedan te isti trougao posmatran sa različitih mesta nije jednak sam sebi. Aman bre ljudi šta to vi pričate?
Pa kada su onda uopšte dve stvari jednake? [ Nedeljko @ 07.06.2009. 21:16 ] @
Formalno, holononi je u pravu. U matematici su objekti A i B jednaki ako A i B nisu dva objekta, nego jedan te isti objekat. No, to ne znači da nakon razjašnjenja postavke holononi nije mogao da razume formulaciju da je hteo da čita poruke.
[ ptak 13. @ 18.06.2009. 17:06 ] @
A kako bi bilo da nastavimo diskusiju sa nekim novim zadatkom umesto rekla kazaal moderator u svetu i kod nas a ....  
Evo vam zadatak jedan da se malo smirite i razmisljate....
Dva casovnika su navijena 4.aprila 1987. godine u 9h ujutru. Jedan od njih radi tacno, a drugi svakog sata napreduje 3 minuta. Kog dana i u koliko sati ce oba casovnika ponovo pokazivati isto vreme ?
Ja se mucim i nikako da ga resim, mora da negde gresim pa ajde probajte vi  [ holononi @ 18.06.2009. 17:46 ] @
Ako je "starinski" sa kazaljkama, 14. aprila će oba pokazivati 09:00h samo što će na bržem biti "9 uveče", inače za 24h clock 24. aprila oba 09:00h.
[ diplodok @ 07.08.2009. 22:04 ] @
Nadovezaću se, da ne otvaram novi temu.
sin (pi) = e^0 - 1
Postoji li neka elegantnija jednakost koja povezuje e, pi, 1, 0.
[ mulaz @ 09.08.2009. 20:59 ] @
Ne znam dali je vec bilo.. ali evo...
Imas niz n binarnih brojeva (a1, a2, a3 ... an), i svi su 0
onda redom negiras sve brojeve deljive sa i, gde i ide od 1 do n
i napisi sve 'n'-eve gde je an==1
znaci recimo za n=5
00000
i=1 (negiras sve)->
11111
i=2 (negiras 2,4,6,..)->
10101
i=3 (negiras 3,6,9,...)->
10001
i=4 (negiras 4,8,16...)->
10011
i=5 (negiras 5,10,15,...)->
10010
znaci rezultat= {1, 4} (jer su samo a1 i a4 jednaki '1')
Moze neko da napamet izracuna za recimo n=100? :) n=1000? :)) prilicno je jednostavno :)
Inace ovaj zadatak je bio na TheDailyWtf :)
[ Daniel011 @ 18.08.2009. 16:16 ] @
Citat: diplodok: Postoji li neka elegantnija jednakost koja povezuje e, pi, 1, 0. 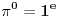
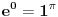 [ ptak 13. @ 18.08.2009. 18:53 ] @
Svaka cast...zanimljivo  !
[ galet@world @ 22.08.2009. 13:57 ] @
Evo jednog interesantnog zadatka iz fizike u vezi sa Doplerovim efektom
U razgovoru sa jednim mojim prijateljem tvrdio sam da nemamo dokaza da se Univerzum
SADA širi, odnosno možda je već počelo sažimanje Univerzuma, ali ni to ne znamo jer dok
sa dalekih vasionskih objekata dođe svetlost sa značajnim ljubičastim pomakom treba da
prođe golemo vreme.
Ne, rekao je on. Mi možemo odmah da konstatujemo sažimanje Univerzuma čim počne jer bi
se ono događalo u celom Univerzumu.
Kako? Upitah.
Jednostavno - odgovori on - jer bismo u davno poslatoj svetlosti sa nekog izvora koja je
stigla do nas odmah - istog časa - konstatovali ljubičasti pomak jer bi se Zemlja kretala u
susret toj svetlosti, a ne bi "bežala" od nje.
Ja se nisam složio - a šta vi kažete?
[ Nedeljko @ 22.08.2009. 14:22 ] @
Smatram da ovu temu treba premestiti u forum za fiziku.
[ galet@world @ 22.08.2009. 20:14 ] @
Ili je treba odmah zaključati?
[ Nedeljko @ 22.08.2009. 22:29 ] @
Tvoje pitanje je sasvim na mestu, ali spada u oblast fizike, a ne matematike. Ako baš hoćeš, smatram da si u sporu sa svojim prijateljem ti u pravu, a ne on, jer je za talasnu dužinu svetlosti koja je emitovana davno, a primljena danas relevantno kretanje Zemlje danas u inercijalnom sistemu (dakle, koji nije međuvremenu ubrzavao) u kome je izvor mirovao u trenutku emitovanja, ali to spada u oblast fizike.
[ galet@world @ 23.08.2009. 06:38 ] @
Citat: Nedeljko: ...jer je za talasnu dužinu svetlosti koja je emitovana davno, a primljena danas relevantno kretanje Zemlje danas u inercijalnom sistemu (dakle, koji nije međuvremenu ubrzavao) u kome je izvor mirovao u trenutku emitovanja, ali to spada u oblast fizike.
Znam da spada u oblast fizike, nemam ništa protiv da se tamo prebaci, ali mi se čini da je interesantan i kao logički zadatak
- to nije sporno - nego običaj da se moje teme rado zaključavaju.
Nisam razumeo tvoj odgovor. Pretpostavili smo da se neki daleki izvor u trenutku emisije pre mnogo vremena udaljavao od Zemlje.
Ili da probamo ovako:
Ako je, na primer, pre mesec dana počelo sažimanje Univerzuma (zanemarimo činjenicu da bi pre toga trebalo da uspori širenje pa da stane
i da posle krene u sažimanje) mi SADA ili ODMAH ne možemo o tome ništa znati jer još uvek primamo davno emitovanu svetlost koja ima
crveni pomak, a svetlost koja ima značajan ljubičasti (plavi) pomak koju bismo mogli detektovati stići će u dalekoj budućnosti.
Čak bi trebalo da u nekom vremenu vidimo sa bližih vasionskih objekata plavi pomak a sa dalekih i dalje crveni, međutim, on kaže (moj
prijatelj) da bismo mogli odmah to saznati jer bi svetlost koja je davno emitovana sa objekata, koji su se u vreme emisije udaljavali
i koja je stigla do nas, morala imati odmah ljubičasti pomak jer se Zemlja SADA (zbog sažimanja koje je u toku) kreće prema toj svetlosti
tako da ta davno poslata svetlost (a koja je stigla do nas) mora SADA imati plavi pomak ako je analiziramo.
(ne znam da li treba reći ljubičasti ili plavi pomak, ali to nije bitno) [ Nedeljko @ 24.08.2009. 09:13 ] @
Ako Marko trči po zemlji u susret svetlosti, a Jovan stoji na zemlji, njih dvojica neće videti nistu talasnu dužinu. Drugim rečima, crveni pomak nije svojstvo svetlosti, bez uzimanja u obzir kretanja prijemnika.
Treba izabrati jedan inercijalni sistem i razmotriti širenje svemira u njemu. Relevantne su brzina predajnika u trenutku emitovanja i brzina prijemnika u trenutku prijema u istom inercijalnom sistemu.
[ galet@world @ 26.08.2009. 07:17 ] @
Ali Nedeljko pitanje je bilo - ko je u pravu - on ili ja
ili ako smo obojica u pravu onda se postavlja pitanje
kad je on u pravu a kad ja.
[ Nedeljko @ 27.08.2009. 18:19 ] @
Ja mislim da si ti u pravu, ali neka on da jednačine širenja u bar jednom inercijalnom sistemu, pa da vidimo.
[ Slobica8990 @ 03.10.2009. 01:05 ] @
a jel moze 2+2+ 2 ( na nulti ) = 5
[ djolas ba @ 08.04.2010. 23:02 ] @
Žena koja je imala 2 ćerke, umire. Na njenu sahranu dolazi čovek obučen u crno, u koga se jedna od ćerki zaljubljuje. Medjutim on nestaje posle sahrane i više ga nisu videle. Posle nekog vremena, jedna ćerka ubija drugu. Zašto?
ako neko zna resenja bio bih mu zahvalan da odgovori pozZzdrav :P
[ Bojan Basic @ 08.04.2010. 23:05 ] @
Nada se da će se čovek pojaviti na sestrinoj sahrani (iz istog razloga iz kog se pojavio na majčinoj, koji god to razlog bio).
[ djolas ba @ 09.04.2010. 13:46 ] @
Bojance mashina si :P......daj jos koji odgovor......
1.Kradljivac je precizno isplanirao noćnu pljačku trezora: za 5 minuta je stigao do banke, za 3 minuta ispraznio trezor i krenuo natrag.Zadovoljan zbog uspešno obavljenog posla, lopov je uključio radio u kolima i, kada je čuo muziku, opsovao je i sam se prijavio policiji - znao je da će u svakom slučaju biti uhapšen. Kako ?
2.Mladić i devojka treba da se sastanu u tačno određeno vreme.Devojka zakasni manje od dve sekunde i mladić zbog toga pogine? (Oboje su bili potpuno zdravi.)
3.Otac i dva sina treba da se prebace čamcem na drugu stranu reke.U čamac može da stane ili sam otac ili oba sina zajedno.Kako će sva trojica da pređu na drugu stranu reke?
4.Bandera je visoka 10 metara.Puž kreće od dna i penje se 3 metra u toku dana, a u toku noći puž sklizne 2 metra.Koliko mu dana treba da se popne na vrh bandere?
ja ili sam totalni kreten ili ne citam dovoljno po forumima...ali ja ni na jedno ne znam odgovoriti.........de matere ti malo pojasni neukom :P pozZzdrav
[ djoka_l @ 09.04.2010. 14:09 ] @
Baš i nema neke veze sa matematikom, al ajde...
1. Ne znam odgovor, ali pretpostavljam da je video da je zaboravio rukavice kada je uključio radio, što znači da je ostavio otiske u banci.
2. Mladić i devojka nastupaju na trapezu, devojka zakasni i mladić ne uhvati trapez (ili devojku), pa tresne o zemlju.
3. Prvo se prebace dva sina, jedan ostane na drugoj obali , a drugi se vrati. Onda otac ode na drugu obalu, a sin koji je ostao tamo, vrati se čamcem. Oba sina pređu čamcem na drugu obalu.
4. Za osam dana (i sedam noći). Za jedan dan i jednu noć puž se popne za jedan metar, i tako 7 dana dok ne dođe do visine od 7 metara. Osmi dan se popne još preostala tri metra.
[ djolas ba @ 09.04.2010. 14:19 ] @
msm da nisi ovo trece pitanjce dobro procitao.......:P....a i ovo prvo mi smrdi nes nestima :)
Zadatak 29:
Sam si u sobi sa dvoje vrata i dva brata. Iza jednih vrata se nalaze velike pare a iza
drugih nista. Znajuci da jedan od dvojice brace UVIJEK govori istinu, a drugi UVIJEK
laze (ti neznas koji laze a koji ne) i da obojica znaju gdje se nalaze pare, treba, jednom od njih dvojice, postaviti samo
jedno pitanje da bi sigurno saznao iza kojih vrata su pare.....
.nas'o sam resenja ali ga ne kontam nikako ali nikako....."reci mi sta bi mi tvoj brat rekao da ga pitam gdje su pare "........???? help
[ Bojan Basic @ 09.04.2010. 14:42 ] @
Citat: djolas ba:
msm da nisi ovo trece pitanjce dobro procitao.......:P....
Dobro je pročitao, i tačan mu je odgovor. Nisi razumeo odgovor, udubi se malo više.
Citat: djolas ba:
1.Kradljivac je precizno isplanirao noćnu pljačku trezora: za 5 minuta je stigao do banke, za 3 minuta ispraznio trezor i krenuo natrag.Zadovoljan zbog uspešno obavljenog posla, lopov je uključio radio u kolima i, kada je čuo muziku, opsovao je i sam se prijavio policiji - znao je da će u svakom slučaju biti uhapšen. Kako ?
Kradljivac radi kao didžej na lokalnom radiju. Pustio je pesmu da se vrti i otrčao do banke s idejom da na brzinu završi pljačku i vrati se na radno mesto. Kada je uključio radio, konstatovao je da pesma preskače i da mu je time isplanirani alibi propao (jer bi, da je stvarno na radnom mestu, preduzeo nešto tim povodom).
No, moram pitati, da li je ovo što šalješ stvarno selekcija stvari koje ti se najviše dopadaju, ili se prosto raspituješ za pomoć oko onoga što ne znaš da rešiš? Ukoliko je reč o ovom drugom, ova tema ipak nije za to predviđena. [ Nedeljko @ 09.04.2010. 17:51 ] @
Mislim da je Bojanov odgovor nepotpun ili da je problem bezveze.
[ djolas ba @ 09.04.2010. 21:05 ] @
msm da je zadatak jasan camcem se mogu voziti ili sam otac ili oba sina zajedno........e sada ako vi kazete da moze samo jedan sin onda je valjda tako.:)
Da ovo je stvarno selekcija stvari koje mi se najviše dopadaju :P....:-))))..
a oko ovoga kradljivca.........nisam bas siguran da je odgovor dobar.......ne cini mi se da je didzej tacniji odgovor od toga da je zaboravio rukavice .pozZz...
[ Nedeljko @ 09.04.2010. 23:56 ] @
Mislio sam na ovaj zadatak
Citat: djolas ba: Žena koja je imala 2 ćerke, umire. Na njenu sahranu dolazi čovek obučen u crno, u koga se jedna od ćerki zaljubljuje. Medjutim on nestaje posle sahrane i više ga nisu videle. Posle nekog vremena, jedna ćerka ubija drugu. Zašto?
ako neko zna resenja bio bih mu zahvalan da odgovori pozZzdrav :P
Ili je bezveze ili je ovo rešenje
Citat: Bojan Basic: Nada se da će se čovek pojaviti na sestrinoj sahrani (iz istog razloga iz kog se pojavio na majčinoj, koji god to razlog bio).
nepotpuno. [ Shadowed @ 10.04.2010. 01:16 ] @
Zasto je resenje nepotpuno?
[ Nedeljko @ 10.04.2010. 03:51 ] @
Pa, otkud znam, fali tu još priče. Zašto sestra nije ubila nekog drugog da privuče ljubitelja sahrana ili jednostavno sačekala da neko rikne?
Ne kažem da ne može i ovo da prođe, ali ako je ovo predviđeno rešenje, onda je problem stvarno bezveze.
[ dusans @ 10.04.2010. 11:38 ] @
Ovo pitanje za ubistvo sestre je mali psiho test da bi se videlo da li neko ima mentalitet ubice.
EDIT: U pitanju je hoax koji se pretstavlja kao test za psihopate http://www.snopes.com/inboxer/hoaxes/sister.asp[ semiconductor @ 02.05.2010. 23:53 ] @
pitanje je sasvim ok i odgovor je jedinstven... ovaj zadatak znam od pre 2-3 godine...
ja sam razmisljao 20-ak sekundi i kad sam dosao do tacnog odgovora bio sam siguran da je to to...
cim je lik bio na sahrani njihove majke, verovatno je poznavao tu zenu (ili porodicu), pa je ova roknula sestru
u nadi da ce ovaj opet da se pojavi...
sto se tice pitanja sa dvoje vrata i dva brata...
npr ako A osoba laze, a B osoba govori istinu, bilo koga da pitas, ides suprotno...
sta bi tvoj brat rekao gde se nalaze pare...
-ako pitas osobu A (laze) sta bi njegov brat rekao, on bi slagao bratovljevu istinu
-ako pitas osobu B (govori isitnu) sta bi njegov brat rekao, on bi samo preneo bratovljevu laz...
kako god okrenes, ides suprotno...
jel jasno ili treba malo poblize?
a sta bi sa ovim lopovom? rukavice mi deluju logicno resenje, ali ne bas toliko fascinantno...
i... dajte jos neki zadatak...
[ semiconductor @ 03.05.2010. 15:37 ] @
Crnogorac slep od rodjenja, cuje da u Beogradu postoji tim strucnjaka koji mogu da mu povrate vid.
Krene on iz Bara za Beograd, odrade operaciju, progleda i posle nekoliko dana vrati se vozom kuci.
Kad je voz pristigao u Bar, nadju ga u kupeu mrtvog. Utvrdjeno je da je izvrsio samoubistvo. Zasto?
Resenje nije da se razocarao sta je video i sl...
Bas je lepo i jednostavno resenje :D
[ Bojan Basic @ 03.05.2010. 15:45 ] @
Voz ušao u tunel.
[ semiconductor @ 03.05.2010. 18:35 ] @

dok se ne setim nekih zadataka, ukljucite se... znam da je lepo vreme,
ali male sive celije moramo da treniramo :)
[ galet@world @ 05.05.2010. 10:07 ] @
A može li oblačna noć?
[ vladica djukanovic @ 07.05.2010. 22:14 ] @
e znate li za onaj, trojica likova su se cipovala po 10 maraka kako bi uzeli litar rakije viljamovke, Takovo, medjutim, boca je kostala 25 maraka. ostatak od 5 maraka podjelili su tako da je svakom od njih trojice vracena 1 marka, tako da ispadne da su za bocu dali po 9 maraka. od tih 5 maraka nakon podjele ostalo je 2.
e sad igramo se pa ja kazem ovako trojica ljudi po 9 maraka jeste 27 maraka + 2 marke bice da je 29 maraka. gdje je jos jedna??????
super je tema... srdacan pozdrav
[ semiconductor @ 07.05.2010. 23:13 ] @
ja bih se drugacije igrao :)
po jedna marka koja je ostala kao kusur + 9*3 za rakiju = 30
ili
25 za rakiju + 3 marke kusur + one dve ostatka = 30
[ galet@world @ 10.05.2010. 20:48 ] @
Ovaj je iz naftalina pa evo još jednog sličnog:
Dođe jedan pametan dečak u trgovinu da kupi nožić.
Trgovac mu pokaže jedan manji nožić koji je koštao jedan dinar i jedan veći od dva dinara.
Dečak je imao samo jedan dinar pa je taj dinar dao trgovcu i kupio manji nožić.
Sutradan se predomislio i ponovo otišao kog istog trgovca - tražio je da razgleda i proba
onaj nožić od dva dinara - pa pošto mu se dopao on vrati trgovcu onaj nožić što je koštao
jedan dinar a ovaj skuplji stavi u džep i krenu kući.
Trgovac povika za njim - ej bre zaboravio si da platiš, međutim, dečak mu odgovori - ništa
ja nisam zaboravio - jučer sam ti dao jedan dinar, a sad sam ti dao nožić koji vredi jedan
dinar i to su ukupno dva dinara koliko vredi ovaj skuplji nožić.
PS
Citat:"od tih 5 maraka nakon podjele ostalo je 2."
Nije ostalo 2 - oni su platili 25 i još te dve a to je 27, a ostalo je 3 kao kusur koji nisu platili
već su ga podelili
[Ovu poruku je menjao galet@world dana 10.05.2010. u 22:09 GMT+1]
[ galet@world @ 12.05.2010. 10:39 ] @
Evo još jednog zadatka:
[ Daniel011 @ 13.05.2010. 05:29 ] @
Sličan štos kao kod ovog zadatka. Linija AC ne seče manje kvadratiće tačno po dijagonalama, nego malo "pored" i zbog toga prilikom njihovog transliranja za jedan red niže i za jedan red desno dolazi do malog, jedva vidljivog odstupanja u površini, ali kada se to odstupanje pomnoži brojem tih kvadratića presečenih linijom AC, dobija se površina tog jednog kvadratića razlike.
P.S. Konvertovao sam tvoj .docx u standardni .doc, jer ovde ipak ne koriste svi Office 2007. [ galet@world @ 13.05.2010. 07:41 ] @
Nadam se da se nećeš ljutiti ako budemo malo precizniji. Kod tog zadatka piše:
" 4 razna elementa u TROUGLU", ali tog trougla nema. To nije TROUGAO.
Dakle to nije istina, međutim, ovaj zadatak ne sadrži ništa neistinito.
Citat: ...dolazi do malog, jedva vidljivog odstupanja u površini,
Nema jedva vidljivih odstupanja u površinama delova presečenog kvadrata -
druga stvar je u pitanju. Koja?
[ Daniel011 @ 13.05.2010. 20:42 ] @
Prevideh jednu stvar, a to je da, ako trougao 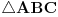 pomerimo za jedan red nadole, a zatim za jedan red nadesno, mi ga zapravo transliramo za 45º. Međutim, duž 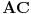 nije pod nagibom od tačno 45º, već pod nekim nagibom koji malo odstupa od 45º (tačan nagib je 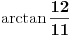 ), tako da transliranjem trougla  za 45º, mi ga zapravo ne transliramo duž pravca  , već će doći do nekog malog preklapanja između ova dva dela velikog kvadrata. Površina na kojoj će se ova dva dela preklopiti biće jednaka površini tog jednog, "nedostajućeg" kvadrata.
Lep zadatak, mada me i dalje neodoljivo podseća na onaj zadatak sa trouglom (tj. trapezoidom koji "liči" na trougao). Ali, dopuštam da je to već moj subjektivan utisak.  [ galet@world @ 13.05.2010. 21:22 ] @
Citat: Daniel011: Površina na kojoj će se ova dva dela preklopiti biće jednaka površini tog jednog, "nedostajućeg" kvadrata.
Tako je! Ali ja ne bih bio ja kad ne bih cepidlačio. Radi se o preklapanju
čak triju delova - evo pogledaj uprošćenu sliku i izvini ako gnjavim:
(delove na slici možeš pomerati) [ Daniel011 @ 13.05.2010. 21:47 ] @
Pravo zboriš, preklapa se i taj treći deo, "trouglić" koji prebacujemo.
Svidela mi se ova ilustracija sa pokretnim delovima u Wordu.  [ galet@world @ 19.05.2010. 07:21 ] @
Kaže muž ženi - Za sedam godina imaćemo ukupno 63 godine
a ona njemu - To je tačno, a kad si ti imao toliko godina koliko
ja imam sada bio si dvaput stariji od mene.
Koliko imaju godina svako od njih?
[ Farenhajt @ 19.05.2010. 10:03 ] @
Citat: galet@world: Kaže muž ženi - Za sedam godina imaćemo ukupno 63 godine
a ona njemu - To je tačno, a kad si ti imao toliko godina koliko
ja imam sada bio si dvaput stariji od mene.
Koliko imaju godina svako od njih? 
Mlada se udala, bogme...
Ako je "63" bila omaška u kucanju, sa željom da se napiše "64", onda su odgovori celobrojni - naime 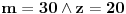
Ali se i u tom slučaju mlada udala... [ galet@world @ 19.05.2010. 15:03 ] @
Farenhajt Bravo!!!
Ja sam rezonovao ovako:
Žena kaže da sada ima toliko godina koliko je on imao kad je bio dvaput stariji od nje
pa je i ona sada dvaput starija od ondašnje sebe.
Ako je imala x godina sada ima 2x godina, a muž je imao 2x godina a sada ima 3x godina
Znači da ukupno sada imaju 5x godina, a ako će za sedam godina imati 63 godine onda
sada imaju ukupno 63 - 14 = 49 godina pa je x = 49 : 5 = 9.8 godina.
Mislim da je broj 63 namerno stavljen da se ne bi tražilo rešenje probanjem.
[ ptak 13. @ 20.05.2010. 18:09 ] @
Pozdrav ljudi 
Imam gadan problem sa ovim zadatkom vec dva dana, ili meni mozak ne radi ili je ovo tezak zadatak 
Ako imam u ormanu 10 pari cipela ( 20 cipela ) svih 10 pari su razliciti. Ako biram uvek 4 cipele, na koliko nacina mogu izabrati 4 cipele a da uvek imam u toj kombinaciji
-bar jedan par cipela ( znaci jedan par i ostalo raspar ili da bas potrefim dva para )
-samo jedan par ( znaci imam jedan par i dve rasprarne )
Jako mi je bitan postupak do resenja.
Nadam se da ste me razumeli !? [ galet@world @ 20.05.2010. 22:01 ] @
Ako sam dobro razumeo zadatak onda cipele u ormanu poređaj, na primer, ovako:
10.....................10
7........................6
9........................9
5........................5
8........................8
3........................4
1........................1
4........................3
2........................2
6........................7
i uzmi cipele iz bilo koja dva susedna reda. Ako nisam razumeo onda nikom ništa - izvini!
[ zzzz @ 20.05.2010. 22:20 ] @
Da počnem.Dva ispravna para možeš imati na 10*9=90 načina.A inače izvlačenjem četiri cipele možeš imati na 20*19*18*17 načina.
Pa ćemo nastaviti za slučaj da imamo jedan par,a drugi raspar.
Jedan od 10 parova*bilo koja (18)*bilo koja osimpara ovoj trećoj (16)
To je 10*18*16.
Da imaš bar jedan par od 4 izvučene cipele može se desiti na
10*9+10*18*16 načina
A može i ljepše.
Izračunamo na koliko načina možemo izvući 4 cipele,a da među njima nema nijedan par.
Prva na 20 načina.
Druga na 18 načina jer ne dolazi u obzir ona iz para.
Treća na ....Četvrta na ...,pa pomnožiti i oduzeti od ukupnog broja načina.
Da nisam šta zabrljao?
[ Daniel011 @ 21.05.2010. 00:25 ] @
Mislim da jesi. Računao si varijacije, a ovde su u pitanju kombinacije.
[ galet@world @ 21.05.2010. 07:11 ] @
Ja možda krivo tumačim reč "način" i zato sam definisao samo jedan od načina, a na taj
način se može izvući više puta četiri cipele koje zadovoljavaju tražene uslove - ali način
je uvek isti - uvek izvlačimo dva susedna reda.
Milan, ako se ne varam, svako izvlačenje samo četiri cipele naziva načinom.
Načina ima manje od izvlačenja
Ili kako kaže Milan - da nisam šta zabrljao?
PS
Citat: zzzz: Da počnem.Dva ispravna para možeš imati na 10*9=90
Molim te pokaži mi kako si ovo izračunao
[Ovu poruku je menjao galet@world dana 21.05.2010. u 09:13 GMT+1][ zzzz @ 21.05.2010. 23:25 ] @
Citat: galet@world:Molim te pokaži mi kako si ovo izračunao Citat: Daniel011: Mislim da jesi. Računao si varijacije, a ovde su u pitanju kombinacije.
Da tako je!Treba 10*4.5=45 načina.a one druge rezultate dijeliti sa 4!. [ ptak 13. @ 22.05.2010. 14:01 ] @
10 * 18 - 10
1 2 2
Ako su parovi AA, BB, CC, DD ……
Bar jedan par da izvucem a uvek izvlacim po 4 cipele
10 pari = 20 cipela
Ali, ako izvucem par AA mogu izvuci druge dve recimo BB, BC, BD itd.
A ako izvucem BB onda druge dve mogu biti AA, AB, AC i sl.
Na osnovu toga cipele AABB i BBAA su jedno te isto pa sam zato oduzeo ovo….
Sta mislite o resenju ? Ako nisam omasio u postavci to bi bilo
( 10 * (18*17)/(2*1))-((10*9)/(2*1) ) = 1530 – 45 =1485 nacina ?!
I ja nemam resenje zato sam ga i postavio, bio je par puta na takmicenjima, na maturskim ispitima i nalazi se u zbirci za prijemni ispit na FONu ali nisam uspeo da nadjem postupno resenje niti resenje konacno, pa sam zato postavio....
[ galet@world @ 22.05.2010. 16:30 ] @
A da nije možda 45 + 165?
E sad raspar može biti obe desne cipele, obe leve, leva i desna i - desna i leva pa treba 165 pomnožiti sa 4.
[Ovu poruku je menjao galet@world dana 22.05.2010. u 17:50 GMT+1]
[ galet@world @ 23.05.2010. 09:19 ] @
Ja sam pogrešio jer me opet zavelo tumačenje reči "način", a tvoje rešenje je po mom
mišljenju tačno jer:
Sa svakim parom može se kombinovati 36 raspara, a to je onda 10 x 36 = 360 kombinacija
pa još pomnoženo sa 4 iznosi 1440 i plus onih par sa parom 45 pa je to ukupno 1485
Citat: Jako mi je bitan postupak do resenja.
Mislim da je iz ovog što sam napisao jasan i postupak. [ zzzz @ 23.05.2010. 09:48 ] @
1485 je dobar rezultat ako se misli na broj mogućih kombinacija u kojima imamo bar jedan dobar par cipela.
Ja to računam ovako:
Ukupan broj kombinacija je
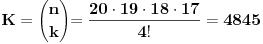
Broj kombinacija koje ne sadrže nijedan dobar par je
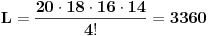
Broj kombinacija koje sadrže bar jedan dobar par je
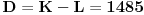 [ galet@world @ 01.06.2010. 12:32 ] @

Od 5 jednakih pravouglih trouglova napravi kvadrat uz uslov da samo
jedan možeš preseći na dva dela. [ Sini82 @ 05.07.2010. 21:47 ] @
Code:
ZADATAK:
Pet mornara i jedan majmun pretrpjeli su brodolom i uspjeli da se domognu nepoznatog ostrva.
Prvog dana oni su vrijedno sakupljali kokosove orahe. Uveče, mornari su složili sve orahe,
kojih nije bilo više od 20000, na jednu gomilu i legli da spavaju ostavljajući za sutradan da ih
ravnopravno podijele. U neko doba noći, kada su svi zaspali, jedan od mornara se probudio i
ustao. On je pomislio da ujutro, pri podjeli oraha, može doći do svađe pa je odlučio da uzme
svoj dio oraha. Razdijelio je sve orahe na pet jednakih dijelova, a jedan orah koji je preostao
dao je majmunu. Zatim je sakrio svoj dio, a sve ostale orahe ponovo je stavio na gomilu.
Poslije nekog vremena probudio se drugi mornar i uradio isto što i prvi mornar. Kod njega je
takođe ostao jedan orah i on ga je dao majmunu. I tako jedan za drugim, postupili su i ostali
brodolomnici. Svaki je iz postojeće gomile uzeo jednu petinu oraha, a preostali orah dao
majmunu. Ujutro su podijelili preostale orahe na pet jednakih dijelova. Opet je ostao jedan
orah koji su dali majmunu. Jasno je da su mornari primjetili da je gomila oraha koje su dijelili
manja nego prethodnog dana, ali kako je kod svakog od njih savjest bila nečista, niko nije
ništa glasno primjetio. Koliko su bili sakupili kokosovih oraha?
Code:
ZADATAK:
Djevojka je udaljena 500 metara od zida a na njenoj glavi odmara se ptica. U jednom momentu
i djevojka i ptica počinju da se kreću pravolinijski prema zidu. Djevojka ide brzinom od 5
metara u sekundi, a ptica leti brzinom od 15 metara u sekundi. Kada ptica dođe do zida, ona
odmah mijenja pravac i vraća se pravo do glave djevojke, mijenja smjer i leti prema zidu. Ovaj
od-glave-do-zida i od-zida-do-glave ptičji let se neprekidno odvija sve dok djevojka ne dođe
do zida. Odrediti ukupnu dužinu puta koji je preletjela ptica, smatrajući da pri zaokretima ne
dolazi do gubitka brzine ptice.
Code:
ZADATAK:
Lav i čovjek, koji se nalaze u areni kružnog oblika, mogu se kretati najbrže brzinom v. Može li
čovjek (ne izlazeći iz kruga arene) odabrati takvu strategiju kretanja da bude siguran da ga
lav nikada neće uhvatiti (pod pretpostavkom da su snage čovjeka i lava neiscrpne)?
[Ovu poruku je menjao Sini82 dana 05.07.2010. u 23:00 GMT+1][ holononi @ 06.07.2010. 18:26 ] @
Citat: Lav i čovjek, koji se nalaze u areni kružnog oblika, mogu se kretati najbrže brzinom v. Može li
čovjek (ne izlazeći iz kruga arene) odabrati takvu strategiju kretanja da bude siguran da ga
lav nikada neće uhvatiti (pod pretpostavkom da su snage čovjeka i lava neiscrpne)?
Bio bi to zaista trapav lav ako bi ostao bez večere. A tom čoveku preporučujem da nabavi bar sekiru ako ne i bazuku ako neće da postane večera.
No ipak ako govorimo o tačkama koje se kreću istom brzinom stvari su nešto drukčije. Prepostavimo da se nalaze na suprotnim stranama arene rastojanje jednako prečniku arene. Za očekivati je da će Lav-tačka da krene pravolinijski prema Čovek-tački. Kada se Čovek-tačka pomeri duž kruga tada i Lav-tačka menja svoju putanju. Stalnim pomeranjem Čovek-tačke duž kruga Lav-tačka reaguje i menja pravac kertanja a time se približava krugu. Medjutim kako su im brzine kretanja jednake a put koji prelazi Lav-tačka je nešto duži bezbedan razmak će uvek da postoji (na kraju se obe tačke kreću po krugu).
Nemojte ovo pokušavati u zoo-vrtu jer lav zna da ide u cik-cak.
[ galet@world @ 06.07.2010. 20:16 ] @
Ali tetiva je uvek kraća od luka!
[ boxxter @ 06.07.2010. 20:34 ] @
Citat: holononi: Medjutim kako su im brzine kretanja jednake a put koji prelazi Lav-tačka je nešto duži bezbedan razmak će uvek da postoji (na kraju se obe tačke kreću po krugu).
Nemojte ovo pokušavati u zoo-vrtu jer lav zna da ide u cik-cak.
Po Zenonu i Aristotelu, lav nikad ne bi stigao coveka. [ holononi @ 06.07.2010. 22:26 ] @
Lav nije čuo ni za Zenona ni za Aristotela pa jadniče ne zna da nemože stići, zato stiže.
@galet@world
Ne posmatraš tetivu već tangentu putanje (kriva) koju opisuje Lav-tačka. Ta tangenta je uvek usmerena na cilj odnosno na Čovek-tačku.
[ galet@world @ 07.07.2010. 05:53 ] @
Citat: holononi: (na kraju se obe tačke kreću po krugu).
A šta se dogodilo sa tangentom koja ne može prolaziti kroz "obe tačke" tog kruga? [ Srđan Pavlović @ 07.07.2010. 06:11 ] @
Lav neminovno stize coveka, iako se krecu istom brzinom.
Ako je tacka A lav, a tacka B covek koji bezi:
Tacka B ne moze pobeci tacki A, jer kad god se ne krece potpuno istim pravcem
i istim smerom kao tacka A, tacka B smanjuje rastojanje. Tacka A naravno uvek se
krece najkracim putem ka tacki B tako odredjujuci pravac kretanja. Posto je ogranicena
kruznicom, tacka B se nikako ne moze vecno kretati istim pravcem kao tacka A, vec
ce morati da skrece svoj pravac i time omoguci tacki A smanjenje rastojanja svaki
put kada je kruznicom primorana na promenu pravca.
Mozda nisam "matematicki" iskazao, ali mi ovo deluje logicno :)
[ boxxter @ 07.07.2010. 06:43 ] @
Ahil i kornjača: „U utrci, najbrži trkač nikada ne može prestići najsporijeg, zato što gonitelj prvo mora doći do tačke odakle je gonjeni pošao, pa prema tome najsporiji uvijek ima prednost.“ (Aristotelova Fizika VI:9, 239b15)
=)
[ galet@world @ 07.07.2010. 08:49 ] @
Mislim da je holononi pogrešio kad kaže da se lav i čovek kreću po istom krugu.
Ako se čovek kreće po obodu arene onda je udaljenost lava od centra arene uvek manja
od radijusa arene t. j. lav i čovek se nikad ne kreću po istom krugu pa lav nikad neće stići
čoveka - ustvari lav se nikad ne kreće kružnom putanjom već spiralnom koja se asimptotski
približava kružnoj.
Ona ptica u drugom zadatku će preći 1500 m (ako negde nisam pogrešio).
Nisam pogrešio jer zadatak je super jednostavan kad se rešava bez niza odnosno reda.
Dok devojka stigne do zida ptica će preleteti tri puta više i gotova priča
[Ovu poruku je menjao galet@world dana 07.07.2010. u 10:21 GMT+1]
[ holononi @ 07.07.2010. 09:12 ] @
Ovaj problem zahteva rešavanje diferencijalnih jednačina. U prilogu je skica ideje.
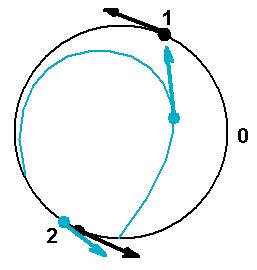
[ boxxter @ 07.07.2010. 09:23 ] @
=) 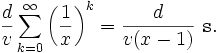 [ Nedeljko @ 07.07.2010. 09:23 ] @
Postoji strategija (sad je se ne sećam), koja ne zahteva rešavanje diferencijalnih jednačina, a koja omogućava čoveku da neograničeno dugo beži. Rastojanje se naravno stalno smanjuje, ali nikada ne dostiže nulu. Zadatak je već bio na ES. Postavila ga je Nervozna.
[ Nedeljko @ 07.07.2010. 09:27 ] @
[ boxxter @ 07.07.2010. 09:32 ] @
Citat: Nedeljko: Postoji strategija (sad je se ne sećam), koja ne zahteva rešavanje diferencijalnih jednačina, a koja omogućava čoveku da neograničeno dugo beži.
Moze da se resi uz pomoc geometrijskih nizova, a glavni faktor je vreme. [ holononi @ 07.07.2010. 09:47 ] @
Ovaj problem je u optimizaciji poznat kao "problem potere". Sličan problem je spajanje modula u orbiti. Medjutim kad govorimo o tačkama bez dimenzija tada do poklapanja nikad ne dolazi iako će njihovo rastojanje biti proizvoljno malo.
[ galet@world @ 07.07.2010. 12:51 ] @
Ako se brzina lava rastavi u dve komponente - jedna paralelna sa trenutnim smerom brzine čoveka
a druga normalna na nju - uvek će komponenta paralelna sa smerom brzine čoveka biti manja iako
se taj odnos menja u korist lava, ali nikad ne dostiže vrednost brzine čoveka (odnosno lava) jer uvek
postoji i normalna komponenta brzine lava na taj smer.
[ holononi @ 07.07.2010. 12:59 ] @
Kad kad si rastavilo lavlje komponente rastavi i za čoveka.
[ galet@world @ 07.07.2010. 15:08 ] @
Citat: holononi: Kad kad si rastavilo lavlje komponente rastavi i za čoveka.
Ne razumem šta si napisao - koriguj rečenicu!
Za prvi zadatak našao sam da su sakupili 3121 ili 16621 orah, ali na kraju nema jedan za majmuna.
Koje je rešenje? [ holononi @ 07.07.2010. 15:33 ] @
Izvini, nesporazum, ne govorimo o istim zadacima.
[ Nedeljko @ 07.07.2010. 15:40 ] @
Citat: galet@world: Za prvi zadatak našao sam da su sakupili 3121 ili 16621 orah, ali na kraju nema jedan za majmuna.
Koje je rešenje?
15621 [ Nedeljko @ 07.07.2010. 16:18 ] @
Neka je n broj oraha koje treba podeliti.
Pošto n-1 mopra biti deljivo sa 5, onda i n+4 mora biti deljivo sa 5, pa je n=5k-4 za neko k. Posle davanja oraha majmuni i skrivanja jedne petine ostaje n'=4k-4 oraha na gomili. Primetimo da je n'+4 deljivo jedanput manje sa 5 nego n+4. Ovo treba uraditi 6 puta, pa je opšte rešenje oblika 56m-4.
[ galet@world @ 07.07.2010. 19:28 ] @
I ja sam našao baš to rešenje - ne znam šta mi je bilo da krivo prepišem t.j. da umesto
petice prepišem šesticu, ali to rešenje ne zadovoljava - evo vidi:
15621 - 3125 = 12496.......prvi mornar
12496 - 2500 = 9996.......drugi mornar
9996 - 2000 = 7996..........treći mornar
7996 - 1600 = 6396..........četvrti mornar
6396 - 1276 = 5120..........peti mornar
5120/5 = 1024.................dele svi i nema ostatka 1 za majmuna, a u zadatku piše da treba da ima.
a to isto može da se dobije i ako je broj oraha 3121 slede vrednosti:
2496, 1996, 1596, 1276, 1020 i opet nema jedan za majmuna
Da mi se nije možda nešto omaklo? [ Nedeljko @ 07.07.2010. 20:07 ] @
6396-1280=5116
[ Nedeljko @ 07.07.2010. 20:12 ] @
Kako si došao do vrednosti 3121?
[ Sini82 @ 07.07.2010. 20:28 ] @
Tačno. Zadatak može da se riješi na više različitih načina.
Citat: galet@world:
Ona ptica u drugom zadatku će preći 1500 m (ako negde nisam pogrešio).
Nisam pogrešio jer zadatak je super jednostavan kad se rešava bez niza odnosno reda.
Dok devojka stigne do zida ptica će preleteti tri puta više i gotova priča
Tačno.
Tačno. Može i matematički da se dokaže.
[ galet@world @ 07.07.2010. 21:53 ] @
Jbg - uvek mi se omakne na ovakvim stvarima - brzopletost. Ja delim 6395 sa 5
bez kalkulatora i bez pisanja i, naravno, zeznem se pa "sračunam" da je to 1275
umesto1279, ili, kao što si video, krivo prepišem cifru - umesto 15621 napišem 16621.
To mi se gotovo obavezno dešava.
Citat: Nedeljko: Kako si došao do vrednosti 3121?
Računao sam za 2 pa za 3 mornara, po istom principu, onako, da bih proverio princip.
Ali usput da pitam - jesi li pokušao da rešiš onaj zadatak koji je bio pre ova tri?
Izgleda da nije interesantan ili ga niko još nije uspeo da reši. [ mokelet @ 08.07.2010. 00:27 ] @
Neka je npr.  duža stranica. Tada je:
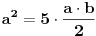
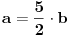
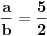
što je i uslov da bi zadatak mogao da se reši.
Tada je rešenje:
 [ Daniel011 @ 08.07.2010. 03:09 ] @
[ galet@world @ 08.07.2010. 07:29 ] @
Bravo momci! Ovo Danijelovo rešenje je zaista lepo.
[ mokelet @ 08.07.2010. 10:23 ] @
Danijele, elegantno rešenje!
Ima i trivijalno rešenje, kada je a=b=0, ali galet@world se ne bi složio sa njim :-D
[ galet@world @ 08.07.2010. 12:32 ] @
Citat: mokelet: Ima i trivijalno rešenje, kada je a=b=0, ali galet@world se ne bi složio sa njim :-D
Naravno da ne bih jer u konkretnom slučaju a nikada nije jednako b
Ma kolika bila stranica a ona je uvek duplo veća od stranice b
Njihov odnos je neuništiv i nezavisan od veličine tog trougla.
Ali za takvu raspravu postoje druge teme pa ovde ne bih o tome. [ mokelet @ 08.07.2010. 12:41 ] @
Citat: galet@world: Naravno da ne bih jer u konkretnom slučaju a nikada nije jednako b
Ma kolika bila stranica a ona je uvek duplo veća od stranice b
Konkretno, nisi ni naveo kakvi su pravougli trouglovi u pitanju, već si u postavci zadatka okačio neku
bezveznu sliku koja ničemu nije poslužila. Eventualno možda kao ukrasna ilustracija.
Tako da je, u skladu sa tvojom postavkom zadatka, sasvim regularno pretpostaviti da je moguće da
bude a=b, a tada je zadatak rešiv kada je a=b=0. [ galet@world @ 08.07.2010. 13:58 ] @
Citat: mokelet: Konkretno, nisi ni naveo kakvi su pravougli trouglovi u pitanju,...
Nije ni trebalo. Sapienti sat! [ Nedeljko @ 08.07.2010. 16:11 ] @
Pa, trebalo je ili da se zada odnos kateta ili da se promeni formulacija zadatka u npr. "Sastaviti kvadrat od 5 podudarnih pravouglih nejednakokrakih trouglova, pri čemu se samo jedan može podeliti na dva dela".
[ mokelet @ 08.07.2010. 16:12 ] @
Naravno da nije trebalo.
Zato je a=b=0 jedno od rešenja zadatka. [ Nedeljko @ 08.07.2010. 16:58 ] @
Ne postoji trougao sa stranicama dužine 0. To po definiciji mnogougla nije mnogougao.
[ mokelet @ 08.07.2010. 17:39 ] @
Naravno da ne postoji, ali algebarski gledano a=b=0 je trivijalno rešenje.
[ galet@world @ 08.07.2010. 17:40 ] @
Citat: Nedeljko: Pa, trebalo je ili da se zada odnos kateta??? ili da se promeni formulacija zadatka u npr. "Sastaviti kvadrat od 5 podudarnih pravouglih nejednakokrakih??? trouglova, pri čemu se samo jedan može podeliti na dva dela".
Nije trebalo - ovo je sasvim dovoljno:
Citat: Od 5 jednakih pravouglih trouglova napravi kvadrat uz uslov da samo jedan možeš preseći na dva dela.
I odnos kateta je deo zadatka koji treba da se reši.
Zadatkom nije stavljena zabrana da se sastavi kvadrat od 5 jednakih jednakokrakih prvouglih trouglova ako se može.
Da vidimo i druga rešenja sa drugim odnosom kateta - samo izvol'te! [ Nedeljko @ 08.07.2010. 18:03 ] @
Ispalo je kao da treba od 5 proizvoljnih podudarnih pravouglih trouglova sastaviti kvadrat, što nije moguće. Trebalo je nekako naglasiti da se pri rešavanju može proizvoljno izabrati odnos kateta.
[ galet@world @ 08.07.2010. 19:44 ] @
Citat: Nedeljko: Ispalo je kao da treba od 5 proizvoljnih podudarnih pravouglih trouglova sastaviti kvadrat, što nije moguće.
Nije tačno da je tako ispalo! Pre svega jednaki su, a zatim pravougli su, a kakav je odnos kateta
diktira zadatak koji treba da se reši. Nigde ne stoji reč proizvoljno.
Citat: Trebalo je nekako naglasiti da se pri rešavanju može proizvoljno izabrati odnos kateta.
Nije trebalo - to bi bilo pogrešno - već taj odnos treba naći odnosno tačno odrediti jer se bez njega
ne može rešiti zadatak!
S kojim još "proizvoljnim" odnosom kateta se može rešiti taj zadatak? [ mokelet @ 08.07.2010. 20:27 ] @
Dobro bre Galet, kada ćeš jednom reći: "U pravu ste, nisam bio dovoljno precizan, pogrešio sam."
Zar je toliko teško to prevaliti preko usana?
Tako kako si formulisao zadatak, pretpostavlja se da su trouglovi PROIZVOLJNI. To što smo mi uradili
zadatak nalazeći prvo odnos kateta samo govori o tome da smo znali na šta si mislio kada si zadao
ovaj zadatak. Zadaj ovaj zadatak srednjoškolcu i misliće da je u pitanju BILO KOJI, odnosno
PROIZVOLJNI pravougli trougao.
Doduše, ja se polako navikavam na tvoju nepreciznost i nedoslednost u izražavanju, ali ne čita samo
par nas ovu temu.
[ galet@world @ 09.07.2010. 06:40 ] @
Citat: mokelet: Dobro bre Galet, kada ćeš jednom reći: "U pravu ste, nisam bio dovoljno precizan, pogrešio sam."
Uvek kada pogrešim.Evo:
Citat: Jbg - uvek mi se omakne na ovakvim stvarima - brzopletost. Ja delim 6395 sa 5
bez kalkulatora i bez pisanja i, naravno, zeznem se pa "sračunam" da je to 1275
umesto1279, ili, kao što si video, krivo prepišem cifru - umesto 15621 napišem 16621. Citat: Zar je toliko teško to prevaliti preko usana?
Kao što vidiš meni to nije teško i ljut sam na sebe što pravim ovakve greške koje nisu posledica
neznanja ili principa rešavanja zadatka već nepažnje i brzopletosti.
Citat: Tako kako si formulisao zadatak, pretpostavlja se da su trouglovi PROIZVOLJNI.
Nema osnova za takvu pretpostavku. To je tvoj proizvoljni odnosno neprincipijelni zaključak.
Evo ti primer za srednjoškolca, za tebe i za Nedeljka:
Od dva jednaka pravougla trougla sastavi pravougaonik.
Treba li ovde dodatak o odnosu kateta? Treba li reći da su trouglovi raznokraki?
Ajde bre ne blamirajte se više!
Citat: Doduše, ja se polako navikavam na tvoju nepreciznost i nedoslednost u izražavanju, ali ne čita samo
par nas ovu temu.
Ti si samo navikao na svoj nedovoljno kontrolisan, nekritičan i neprincipijelan stav. [ holononi @ 09.07.2010. 07:49 ] @
Zadatak može da se tumnači i tako da za bilo kojih "5 jednakih pravouglih trouglova" treba pronaći rešenje. Tada je odgovor da u opštem slučaju to nije moguće. Ako se zadatak tumači pronaći "5 jednakih pravouglih trouglova" tada smo dobili dva rešenja. Na našim fakultetima se ovakvi problemi rešavaju tako što se tresne šakom o sto pa je rešenje onako kako je zamislio profesor bez obzira da li su moguća drugačija tumačenja. Nije čudo što sada imamo kilometarsku raspravu ni oko čega.
[ galet@world @ 09.07.2010. 08:30 ] @
Ajmo još jednostavnije: (za onog iz osnovne škole)
Sastavi kvadrat od dva jednaka pravougla trougla
Kako ovaj zadatak može da se protumači?
[ holononi @ 09.07.2010. 08:58 ] @
Evo ovakio.
Jesu "dva" ? Jesu.
Jesu "jednaka" ? Jesu.
Jesu "pravougla trougla" ? Jesu.
[ Nedeljko @ 09.07.2010. 09:35 ] @
Citat: galet@world: Ajmo još jednostavnije: (za onog iz osnovne škole)
Sastavi kvadrat od dva jednaka pravougla trougla
Kako ovaj zadatak može da se protumači?
To upravo znači da se sastavi pravougaonik od bilo koja dva podudarna pravougla trougla i to jeste moguće. Upravo bi tako đak protumačio tvoj zadatak. [ zzzz @ 09.07.2010. 09:49 ] @
Jel zabranjeno sjeckati trokutove?Nije!
Nađimo stranu kvadrata kome je površina jednaka ab.
Nacrtam polukrug nad prečnikom a+b i podignem visinu na spoju a i b.
To mi je strana kvadrata.A sad hajmo sjeckati trokutove i trpati djelove u onaj kvadrat.Koliko najmanje sleckanja treba?
 [ galet@world @ 09.07.2010. 10:04 ] @
@holononi
A jesu li sastavni delovi kvadrata? Nisu!
Zašto nisi protumačio zadatak do kraja?
Čemu služi polovično tumačenje zadatka? U zadatku postoji i uslov.
Njega si ignorisao. S kojim pravom?
Čak ni onaj iz osnovne škole ne razmišlja kako zadatak ne može
da se reši nego kako može, a da ispoštuje uslov dat zadatkom.
[ holononi @ 09.07.2010. 10:14 ] @
zzzz ti je odgovorio, ja mogu da iscrtam nekoliko rešenja, isto tako i ostali. Ali ne vidim koja svrha.
[ galet@world @ 09.07.2010. 10:19 ] @
Citat: Nedeljko: To upravo znači da se sastavi pravougaonik od bilo koja dva podudarna pravougla trougla i to jeste moguće. Upravo bi tako đak protumačio tvoj zadatak.
Samo ako ne zna šta je kvadrat a šta pravougaonik. [ holononi @ 09.07.2010. 10:55 ] @
A hoćemo opet malo da tamburamo šta je jednakost a šta podudarnost ?
[ galet@world @ 09.07.2010. 11:25 ] @
Citat: holononi: zzzz ti je odgovorio, ja mogu da iscrtam nekoliko rešenja, isto tako i ostali. Ali ne vidim koja svrha.
Ne znam šta je zzzz hteo da kaže jer u ovom zadatku seckanje trouglova
je zabranjeno - samo jedan od zadatih 5 i to jednom sme da se preseče,
odnosno kvadrat treba da bude sastavljen od ukupno šest delova. [ galet@world @ 09.07.2010. 11:33 ] @
Citat: holononi: A hoćemo opet malo da tamburamo šta je jednakost a šta podudarnost ?
To smo već tamburali - ti tvrdiš da je stvar jednaka sama sebi - pa dobro neka ti bude. [ zzzz @ 09.07.2010. 11:38 ] @
Ja sam rješavao ovaj zadatak:
Ajmo još jednostavnije: (za onog iz osnovne škole)
Sastavi kvadrat od dva jednaka pravougla trougla
Kako ovaj zadatak može da se protumači?
Pa pošto su mi se zatekle makaze u ruci od onog zadatka sa 5 trokutova mislio sam da ih treba i ovdje koristiti jer nije rečeno da ih odložim.Ali ni ovdje izgleda ne mogu makaze uvjek pomoći.
[ holononi @ 09.07.2010. 13:57 ] @
Dakle imamo dva jednaka pravougla trougla. Sastavimo kvadrat.
I treba koristiti termin podudartni trouglovi. [ galet@world @ 09.07.2010. 16:17 ] @
Citat: zzzz: Ali ni ovdje izgleda ne mogu makaze uvjek pomoći.
Može ti pomoći ako naučiš da čitaš - šta piše u tom zadatku.
Citat: holononi: Dakle imamo dva jednaka pravougla trougla. Sastavimo kvadrat.
I treba koristiti termin podudartni trouglovi.
A gde su trouglovi? [ Nedeljko @ 09.07.2010. 16:38 ] @
holononi je u pravu, ako su jednaki onda je to jedan trougao, ne mogu biti dva. Međutim, u geometriji se upotreba trmina "jednaki" umesto "podudarni" toleriše, tako da galetova terminologija u tom smislu nije pogrešna.
[ holononi @ 09.07.2010. 17:04 ] @
Ajmo Jovo nanovo. Čim neko kaže jednaki ja pomislim na skupove (ne znam zašto, valjda sam uvrnut) pa ću pitati
- "a u čemu jednaki ?".
Na to će neko odgovoriti
- "Kad kažem jednaki onda mislim po svemu jednaki".
Meni tada neće biti jasno "a jel i po boji ?". I tako u nedogled.
Da bih se navikao referencirajte mi na definiciju jednakosti trouglova.
[ galet@world @ 09.07.2010. 19:00 ] @
Možda će biti lakše ako ti kažeš u čemu je razlika između podudarnih trouglova
[ galet@world @ 09.07.2010. 20:08 ] @
Da se mi ipak vratimo interesantnijim stvarima odnosno na temu
Evo jednog zadatka:
Jedan domaćin treba da posadi 21 šljivu, ali u 12 redova i to tako da u svakom redu bude 5 stabala
Nacrtajte kako treba da izgleda šljivar!
[ Nedeljko @ 09.07.2010. 20:47 ] @
Citat: galet@world: Možda će biti lakše ako ti kažeš u čemu je razlika između podudarnih trouglova
U temenima, ako se ne poklapaju. [ galet@world @ 09.07.2010. 21:27 ] @
Citat: Nedeljko: U temenima, ako se ne poklapaju.
Misliš li na položaj odnosno orijentaciju trouglova? [ holononi @ 09.07.2010. 21:39 ] @
Citat: Da se mi ipak vratimo interesantnijim stvarima
Naravno.
Pretpostavimo da je relacija jednakosti isto što i relacija podudarnosti. Posmatrjamo skupove
A = {(1,0), (2,0)}
B = {(1,0), (2,0)}
Ovi skupovi su očigledno jednaki ali da li važi podudarnost ? [ galet@world @ 09.07.2010. 21:54 ] @
Citat: holononi:Ovi skupovi su očigledno jednaki ali da li važi podudarnost ?
Pre tog pitanja bilo je ovo pitanje:
Citat: Misliš li na položaj odnosno orijentaciju trouglova? [ Nedeljko @ 10.07.2010. 11:15 ] @
Citat: galet@world: Misliš li na položaj odnosno orijentaciju trouglova?
Da, na to gde su im temena.
A=B u matematici znaci da su A i B jedan isti objekat, tj. A je upravo B. [ zzzz @ 10.07.2010. 11:43 ] @
Citat: galet@world:
Jedan domaćin treba da posadi 21 šljivu, ali u 12 redova i to tako da u svakom redu bude 5 stabala
Nacrtajte kako treba da izgleda šljivar!
Da li se kolona smatra redom?Da li red može ići i po nekom kosom pravcu?
Šljivara ne znam nacrtati,ali mislim da je isti kao bukvar.A ovaj ima brkove,šešir,budak i sadi bukve okolo. [ galet@world @ 10.07.2010. 12:44 ] @
Smatra
Može
Ako ne znaš da nacrtaš šljivara nacrtaj šljivančanina
[ mokelet @ 10.07.2010. 12:47 ] @
Šljivik.
[ galet@world @ 10.07.2010. 13:10 ] @
Citat: Nedeljko: Da, na to gde su im temena.
A=B u matematici znaci da su A i B jedan isti objekat, tj. A je upravo B.
Nekako ispada da jednakost i ne postoji, jer jedan te isti objekat nije jednak ni sam sebi
na nekom mestu ako ga premestiš na drugo, ili ako ga na tom istom mestu zarotiraš oko,
recimo, težišta.
On na novom mestu jeste jednak sam sebi, ali nije jednak onom sebi kad je bio na drugom mestu.
Čini mi se da je to ipak preterivanje jer ako govorimo o nekom objektu onda imamo
u vidu njegove konkretne karakteristike bez obzira na položaj i orijentaciju, jer ako bismo
išli i dalje - onda neki trougao nikad nije jednak ni sam sebi pošto bismo mogli reći da se
svakog trenutka nalazi u drugom vremenu - ako već vreme smatrate dimenzijom. [ galet@world @ 10.07.2010. 14:08 ] @
Malo o jeziku ( usput - neće škoditi):
Da zzzz ne bi crtao neke tamo šljivančanine i bukvane! U srpskom jeziku se upotrebljavaju za voćnjak šljiva reči: šljivar, šljivak ili šljivik
a u hrvatskom šljivik, mada se u Lici kaže šljivar, a za čoveka se kaže šljivar ili Šljivar (kao prezime) sa kratko silaznim akcentom
a voćnjak šljivar se izgovara sa kratko uzlaznim akcentom. Nije tema, ali moram pomoći zzzz-u da reši zadatak i da odgovorim na
njegovo "dobronamerno" pitanje.
[ mokelet @ 10.07.2010. 14:37 ] @
Citat: galet@world: Nekako ispada da jednakost i ne postoji, jer jedan te isti objekat nije jednak ni sam sebi
na nekom mestu ako ga premestiš na drugo, ili ako ga na tom istom mestu zarotiraš oko,
recimo, težišta.
On na novom mestu jeste jednak sam sebi, ali nije jednak onom sebi kad je bio na drugom mestu.
Čini mi se da je to ipak preterivanje jer ako govorimo o nekom objektu onda imamo
u vidu njegove konkretne karakteristike bez obzira na položaj i orijentaciju, jer ako bismo
išli i dalje - onda neki trougao nikad nije jednak ni sam sebi pošto bismo mogli reći da se
svakog trenutka nalazi u drugom vremenu - ako već vreme smatrate dimenzijom.
Dosadan si. [ holononi @ 10.07.2010. 14:40 ] @
Kod podudarnih duži srednja tačka je podjednako udaljena od krajnjih tačaka. Medjutim za skupove koje sam naveo srednja tačka (3/2,0) ne pripada tim skupovima koji su očigledno jednaki. Prema tome imamo jednake skupove na koje ne možemo da primenjujemo staviove o podudarnosti.
Zato jednakost i podudarnost nisu sinionimi.
[ galet@world @ 10.07.2010. 17:34 ] @
Citat: holononi: Zato jednakost i podudarnost nisu sinionimi.
Slažem se, uostalom to sam i ranije već rekao. Hteo bih da iznesem svoje mišljenje o tom.
(ne obazirući se na bezvredne primedbe nekih učesnika). Ako su dva podudarna trougla različito
orijentisana i ako su na različitim mestima onda oni nisu jednaki u odnosu na druge objekte.
Dakle taj odnos prema drugim objektima čini ih nejednakim iako su podudarni.
Da li imaš primedbu na ovakav zaključak ili njegovo preciznije konkretizovanje?
E sad - činjenica je da u definiciju trougla ne ulazi ni njegov položaj ni orijentacija i otuda
sledi "jednakost" za koju Nedeljko kaže da se ipak toleriše kao sinonim za podudarnost. [ holononi @ 10.07.2010. 19:25 ] @
Duži se mogu skupovima predstaviti segmentima realne prave na primer [1,3] i [11,13]. Ove duži su podudarne ali navedeni skupovi nisu jednaki.
Kod geometrijskih objekata pojedine mere mogu biti jednake, dužina, površina itd. Ali to ne povlači uvek podudarnost.
[ galet@world @ 10.07.2010. 20:09 ] @
Citat: holononi: Duži se mogu skupovima predstaviti segmentima realne prave na primer [1,3] i [11,13]. Ove duži su podudarne ali navedeni skupovi nisu jednaki.
Odnosno ti segmenti realne prave nemaju isti odnos prema bilo kom trećem segmentu te prave ili bilo čemu drugom.
Citat: Kod geometrijskih objekata pojedine mere mogu biti jednake, dužina, površina itd. Ali to ne povlači uvek podudarnost.
Naravno, dužine kružnog luka i nekog segmenta realne prave mogu biti jednake ali te duži nisu podudarne i sl. [ vlada_vlada @ 11.07.2010. 14:30 ] @
Skupom tacaka { (0,0), (0,1), (1,0) } je odredjeno beskonacno mnogo trouglova. Svi oni koegzistiraju unutar istog geometrijskog prostora. Ovo nije intuitivno, ali je matematicki ispravno. Kazemo da su svi ti trouglovi jednaki.
Kao sto je npr. kordinatom (0,0) odredjeno beskonacno mnogo tacaka - nula kordinatnog sistema...
[ srdjan.v @ 14.07.2010. 13:07 ] @
Ja sam dobio da su sakupili 19530 oraha
[ galet@world @ 14.07.2010. 19:09 ] @
Pa to je odmah deljivo sa 5 - nemaš ostatak 1
[ srdjan.v @ 14.07.2010. 20:04 ] @
Tacno, nisam sabrao onaj jedan u prvom krugu sto je prvi mornanar dao majmunu. Euforija kada sam izracunao :))
tacan broj je 19531. Krenuo sam od pozadi da racunam kada sam postavio jednnacinu i nisam njeega na kraju sabrao.
[ galet@world @ 15.07.2010. 07:50 ] @
19531 - 1 - 19530/5 = 19531 -1 - 3906 = 19531 - 3907 = 15624 i šta ćemo sad?
[ srdjan.v @ 15.07.2010. 08:38 ] @
Ajde da probam da objasnim moju logiku.
Znaci oni su sakupili manje od 20000 neka to bude 20000-n ukupno oraha.
Prvi mornar:
((2000-n)/5) + 1= A
A- broj oraha koji je ostao drugom mornaru
Drugi mornar:
(A/5) + 1 =B
B-broj oraha za treceg mornara
Treci Mornar:
(B/5) +1= c
Cetvrti mornar:
(C/5) + 1=D
Peti mornar :
(D/5) +1=E
i sad na kraju
(E/5) + 1= 0
i odavde dobijes da je E=-5
Vratis u nazad i dobijes rezultat
To je bila moja ideja, reci mi ako negde gresim
[ Nedeljko @ 15.07.2010. 08:45 ] @
Naravno da grešiš, jer ti rezultat nije tačan, što se direktno proverava, kao što je galet to pokazao.
[ srdjan.v @ 15.07.2010. 08:49 ] @
Zaboravih da kazem, vretis se unazad da odredis n
[ Nedeljko @ 15.07.2010. 09:46 ] @
19531 nije rešenje.
1. Kad jedan orah daš majmunu, ostane ti 19530.
2. Petina od preostalog je 3906 oraha.
3. Kada se ta petina odbije, ostaje 15624 oraha.
4. Daj jedan orah majmunu i ostaje 15623 oraha.
5. 15623 nije deljivo sa 5.
[ galet@world @ 15.07.2010. 13:59 ] @
Citat: srdjan.v: Ajde da probam da objasnim moju logiku.
To je bila moja ideja, reci mi ako negde gresim
Grešiš u tome što deliš na 5 delova onoliko koliko mornari uzimaju a ne ono što ostaje
Evo gledaj:
19531 -1 = 19530
19530/5 =3906 to je uzeo prvi mornar
3905/5 = 781 to bi drugi mornar uzeo iz džepa prvog (ili toliko iz ostatka)
780/5 = 156 to bi uzeo treći mornar iz džepa drugog i t. d.
155/5 = 31
30/5 = 6
5/5 = 1 i od šestice ostane 1 za majmuna.
Ti si rešio drugi zadatak, a ne onaj koji je postavljen. [ Agnus Dei @ 21.10.2010. 16:26 ] @
[ Agnus Dei @ 21.10.2010. 16:49 ] @
Stanar zgrade koji zivi na 11. spratu redovno silazi liftom po hranu i novine, ali kad se vraca u svoj stan liftom ide samo do 8. sprata, a onda nastvalja pesaka.
Zasto?
[ plague @ 21.10.2010. 23:18 ] @
Znamo svi ovo. Jer je "mala osoba" pa moze da dohvati samo do broja 8. :]
[ Agnus Dei @ 21.10.2010. 23:28 ] @
Tako sam i mislio... :D
Ajd sad zadatak iz mog prethodnog posta....
[ edisnp @ 26.10.2010. 19:48 ] @
ovaj 8 zadatak je bas super
msm da f(x)=x
[ Fermion @ 08.12.2010. 10:07 ] @
Da aktiviram ovu temu jednim jako zanimljivim (ali i poznatim) zadatkom.
Code:
Napisano je n pisama i poslato je na n adresa u n koverata. Na koliko je načina moguće rasporediti ova pisma tako da svako bude u pogrešnoj koverti? [ Sini82 @ 09.12.2010. 12:59 ] @
Ukupan broj mogućih rasporeda je 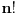 . Neka je 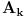 skup svih rasporeda kod kojih  -to pismo stiže na pravo adresu.
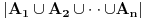 je broj rasporeda u kojima postoji bar jedno pismo koje je stiglo na pravu adresu.
Broj rasporeda koji mi tražimo je 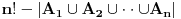 .
Kako je broj rasporeda kod kojih fiksiranih 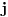 pisama stiže na pravu adresu, jednak 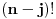 , na osnovu formule isključivanja i uključivanja dobijamo da je traženi broj rasporeda 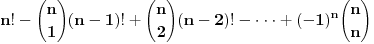 .
Malo ću da preformulišem zadatak (prodiskutovati slučaj kada n teži beskonačno):
Code:
Napisano je n pisama i poslato je na n adresa u n koverata. Kolika je vjerovatnoća da svako
pismo bude raspoređeno u pogrešnoj koverti? [ Fermion @ 09.12.2010. 22:08 ] @
Svaka čast, to je tačno rešenje!
Ovo je inače problem koji je formulisali i rešavali Bernuli i Ojler.
Zadatak sa verovatnoćom mi je poznat, stoga zasad još neću da pišem rešenje.
[ Sini82 @ 10.12.2010. 13:27 ] @
Poznat mi je taj zadatak otprije, bio je na takmičenjima.
Citat: Fermion:
Ovo je inače problem koji je formulisali i rešavali Bernuli i Ojler.
Ovo nisam znao. [ atelago @ 19.01.2011. 11:07 ] @
Ne može se konstruisati svaki ugao niti neki proizvoljan ugao podeliti na tri dela,
ali to nije smetnja da se praktično napravi dovoljno tačan uglomer.
Kako?
[ Sini82 @ 19.01.2011. 12:47 ] @
[ Sini82 @ 19.01.2011. 13:03 ] @
Student pita profesorku: "Koliko su ti stare kćerke?"
Profesorka odgovara: "Ako pomnožiš njihove godine dobićeš 36. Ako ih sabereš, dobićeš broj tvoje kuće."
"Nedostaje mi detalj.", protestuje student.
Profesorka odgovara: "U pravu si, najstarija svira klavir."
Koliko su stare tri kćerke?
Zadatak je iz filma La habitacion the Fermat.
[ Fermion @ 19.01.2011. 15:43 ] @
Ovo mi se čini prosto, ali možda nešto ne uviđam ovako na brzinu.
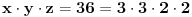
Pošto psotoji najstarija postoji najveći broj među x,y,z. Tako se isklljučuje 6,6,1.
Ostaje (1,4,9), (12,3,1), (6,3,2), (9,2,2).
S obzirom da student zna broj svoje kuće on može da odredi o kojoj kombinaciji brojeva se radi, jer zbir je kod sve četiri kombinacije različit, sledi da je rešenje jednoznačno određeno. [ Nedeljko @ 19.01.2011. 16:06 ] @
Nisi uračunao da bez odbacivanja mogućnosti 6,6,1 rešenje nije bilo jednoznačno određeno. To znači da je broj kuće 13. Dakle, rešenje je 9,2,2.
[ Fermion @ 19.01.2011. 16:15 ] @
Citat: Nedeljko: Nisi uračunao da bez odbacivanja mogućnosti 6,6,1 rešenje nije bilo jednoznačno određeno. To znači da je broj kuće 13. Dakle, rešenje je 9,2,2.
Da... Tako mi i treba kad isprva nisam pročitao pola zadatka i uopšte nisam primetio taj deo kad student kaže da mu nedostaje detalj. [ Sini82 @ 19.01.2011. 18:56 ] @
Citat: Fermion:
Tako se isklljučuje 6,6,1.
Ne isključuje se tako. [ Nedeljko @ 19.01.2011. 21:21 ] @
U slučaju 6,6,1 ne bi postojala najstarija koja svira klavir. To znači da je ta mogućnost isključena.
[ Sini82 @ 19.01.2011. 21:52 ] @
Da li?
[ atelago @ 19.01.2011. 22:30 ] @
Smatra se da su bliznakinje jednako stare.
Ali nije odgovoreno na zadatak kako napraviti uglomer tako da možemo
i nacrtati i izmeriti uglove od 0 do 360 stepeni
Trisekcija ugla je drugo pitanje, a ovde se stvarno radi o uglomeru koji
možemo napraviti vrlo precizno kao onaj iz dućana ili još bolje.
Hajde majstori!
[Ovu poruku je menjao atelago dana 19.01.2011. u 23:48 GMT+1]
[ Sini82 @ 19.01.2011. 22:48 ] @
Kako si zaključio da su blizankinje. Obrazloži, nigdje u zadatku nije rečeno.
[ Fermion @ 19.01.2011. 22:59 ] @
Ja sam mogućnost sa bliznakinjama isključio imajući u vidu da iako su podjednako stare, nijedna nije starija od obe preostale, pa nemožemo je nazvati najstarijom. Ovo je već stvar terminologije, ali logičnije mi je da bude onako kako sam rekao, uz Nedeljkovu popravku.
[ atelago @ 19.01.2011. 23:16 ] @
@ sini
Ne odnosi se na zadatak nego na rešenje: 6, 6, 1
jer ako ćemo cepidlačiti onda jedna od blizankinja nema tačno 6 godina,
pa proizvod nije tačno 36, ili ako hoćemo da proizvod bude tačan onda ni
jedna blizankinja nema tačno 6 godina
[ Sini82 @ 21.01.2011. 18:21 ] @
@atelago
Mogu obe imati isti broj godina, recimo 6, a da jedna bude starija od druge. To uopšte ne utiče na proizvod godina.
@fermion
Zadatak ima jedinstveno rješenje i pod uslovom da mogu imati isti broj godina a da jedna bude starija od druge. Moguće je i da nisu blizankinje, ako jesu i to je dio rješenja; treba ga u potpunosti obrazložiti.
[ atelago @ 21.01.2011. 21:08 ] @
U zadatku se za meru prećutno uzima jedna cela godina, (godina kao komad!), pa sve što je
preko toga ne uzima se u obzir ni na koji način – stoga je pod tim uslovom jedino
rešenje 9, 2, 2 iako je tu problematična reč “najstarija” jer inicira drukčiju meru i drukčija rešenja.
Ovih dilema ne bi bilo kad bi se tražilo koliko jabuka ima u tri pakovanja a pakovanje
s najvećim brojem jabuka ima sliku stabla.
Hajd’ sad da napravimo uglomer i što je još interesantnije da izvršimo n-sekciju bilo kog
ugla od 0 do 2π bez iskazivanja koliki je taj ugao u stepenima, radijanima i sl.
[ Sini82 @ 25.01.2011. 22:52 ] @
Student pita profesorku: "Koliko su ti stare kćerke?"
Profesorka odgovara: "Ako pomnožiš njihove godine dobićeš 36. Ako ih sabereš, dobićeš broj tvoje kuće."
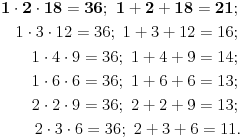 "Nedostaje mi detalj.", protestuje student.
"Nedostaje mi detalj.", protestuje student.
Profesorka zna broj studentove kuće. Zašto njemu ta informacija nije dovoljna da zna koliko godina imaju kćerke? Zato što ima više mogućih slučajeva kada je proizvod njihovih godina 36 a zbir jednak broju njegove kuće. Zaključujemo da je broj njegove kuće 13 jer je to jedini takav slučaj da su zbirovi godina za različite mogućnosti isti. Dakle, kćerke imaju dvije 6 godina a jedna 1 ili dvije 2 godine a jedna 9.
Profesorka odgovara: "U pravu si, najstarija svira klavir."
Jasno da je to taj detalj koji nedostaje. Zašto? Jer student ima jednu informaciju koju mi nemamo. Dvije sestre su blizankinje. U suprotnom, imali bi dva moguća slučaja i ne bi mogli da odredimo koliko kćerke imaju godina; u prvom slučaju, mogu dvije kćerke da imaju obe 6 godina ali da je jedna par mjeseci (najmanje 9, osim ako je mlađa ranije rođena) starija od druge; u drugom slučaju je najstarija ona koja ima 9 godina; i za onu od 6, kao i za onu od 9 godina, moguće je da sviraju klavir.
Koliko su stare tri kćerke?
Najstarija ima 9 godina, dvije mlađe su blizankinje i imaju po 2 godine.
[ Nedeljko @ 25.01.2011. 23:43 ] @
Citat: Sini82: i za onu od 6, kao i za onu od 9 godina, moguće je da sviraju klavir.
I kako onda po toj logici student utvrđuje koju je slučaj u pitanju? [ petarm @ 26.01.2011. 01:34 ] @
Racuna se da su jednako stare, ako imaju jednako godina. Samim tim ima smisla i pricati o proizvodu godina.
[ Nedeljko @ 26.01.2011. 07:25 ] @
Po njegovoj logici, gde mogu biti različite starosti sa istim brojem godina.
[ Sini82 @ 26.01.2011. 12:21 ] @
Kćerke imaju x, y, z godina i p, q, r mjeseci, respektivno.
Kada sabiremo ili množimo godine, računamo sa x, y i z. Kada gledamo koja je kćerka starija, uzimamo u obzir i mjesece. Tako je to u realnom svijetu.
[ petarm @ 26.01.2011. 14:57 ] @
Da li ti u realnom svetu znas koji je od blizanaca ili bliznakinja stariji? Ja ne znam. Znam nekoliko blizanaca i bliznakinja i racunam ih kao da su jednako stari. Ne pitam ko je od vas dvojice (dvoje, dve) stariji ili pre izasao?
[ Nedeljko @ 26.01.2011. 15:25 ] @
Citat: Sini82: Kćerke imaju x, y, z godina i p, q, r mjeseci, respektivno.
Kada sabiremo ili množimo godine, računamo sa x, y i z. Kada gledamo koja je kćerka starija, uzimamo u obzir i mjesece. Tako je to u realnom svijetu.
Izuzev u slučaju blizanaca, ta logika je OK, ali onda se tvoje rešenje ne uklapa u tu logiku. Kako si onda zaključio da informacija da najstarija svira klavir izdvaja jedno od rešenja 6,6,1, odnosno 9,2,2? Sam si rekao da u oba slučaja može najstarija da svira klavir. [ Sini82 @ 26.01.2011. 16:50 ] @
@petarm
Govorimo o godinama i mjesecima ne o danima, satima, minutama, sekundama... Ako su blizanci, podrazumijeva se da su se zajedno rodili, da su iste starosti (istovremeno počinju da žive još prije rođenja od kada se podijelila jajna ćelija, da sad ne filozofiramo oko toga). Sestre po majci mogu imati razliku u starosti najmanje u mjesecima, nikako u danima ili manjim vremenskim jedinicama. Zato se starost kćerki poredi u godinama i mjesecima.
Citat: Nedeljko:
I kako onda po toj logici student utvrđuje koju je slučaj u pitanju?
Nikako.
Dokazao sam, svođenjem na protivrječnost, da dvije kćerke moraju biti blizankinje. Inače, detalj koji je nedostajao ne bi bio dovoljan, kao što si i sam zaključio. Postavio sam tvrdjenje da su dvije sestre blizankinje. Sledeću rečenicu sam počeo sa: "U suprotnom..." (rečenica završava sa tačkom). Student je to znao, kao što je i profesorica znala broj njegove kuće. Zato mu je bilo dovoljno da zna da najstarija kćerka svira klavir. Pošto sada znamo da su dvije kćerke blizankinje, lako dolazimo do rješenja zadatka. [ Nedeljko @ 26.01.2011. 18:25 ] @
Citat: Sini82:
Nikako.
...
Zato mu je bilo dovoljno da zna da najstarija kćerka svira klavir.
Da rezimiramo: Iz te informacije ne može nikako da izvuče zaključak, ali mu je ta informacija dovoljna da izvuče zaključak. Je l' ti zezaš ili ja nešto ne razumem. Zašto ne može jedna ćerka da ima 1 godinu, a preostale dve po 6 i da nisu bliznakinje? [ Sini82 @ 27.01.2011. 09:56 ] @
Jel' ti mene zezaš, il' stvarno ne razumiješ? Kao da čitaš moje postove na pola, vadiš dijelove iz konteksta i citaraš ih. Poenta je da ako je student došao do jedinstvenog rješenja, dvije sestre moraju da budu blizankinje.
Citat: Nedeljko:
Zašto ne može jedna ćerka da ima 1 godinu, a preostale dve po 6 i da nisu bliznakinje?
Zato što su onda rješenja (9,2,2) i (6,6,1) ravnopravna, student ne bi mogao da odredi koliko kćerke imaju godina (rješenje ne bi bilo jedinstveno). To ne dolazi u obzir, jer je poslednja informacija koju je dobio detalj koji je nedostajao da odredi koliko imaju godina. Dakle, rješenje postoji i jedinstveno je. Nameće se jedini mogući zaključak, da dvije sestre jesu blizankinje. Jasno je da onda najstarija kćerka ima 9 godina a druge dvije su blizankinje i imaju po 2 godine. [ X Files @ 27.01.2011. 10:21 ] @
U tekstu zadatka meni je najnelogičnije što konačno pitanje ("Koliko su stare tri kćerke?") ima u sebi ugrađenu konstantu 3, koja ne proističe iz dijaloga (kad su ga već dali).
[ Sini82 @ 27.01.2011. 10:55 ] @
U pravu si. Razmišljao sam o tome, došao sam do zaključka da student poznaje njene kćerke (kao što i profesorica zna broj njegove kuće). Zato se konstanta 3 u njihovom razgovoru podrazumijeva (prešućuje). Nije isključeno da su kćerke bile prisutne tokom njihovog razgovora. Ako pretpostavimo da je tako, student je znao da su blizankinje, za razliku od nas koji moramo to da logički zaključimo (jer kada ne bi bile dve od njih blizankinje, jasno je da student tada na osnovu razgovora ne bi mogao da odredi koliko kćerke imaju godina, što sam već obrazložio).
[ atelago @ 27.01.2011. 11:43 ] @
Konstanta 3 nije ni potrebna jer kad bi bile dve ćerke onda nema najstarije, a za
4 ćerke dodatna informacija je nedovoljna , a za 5 i vise ćerki ne bi ni trebalo dodatne
informacije kad bi mu bio broj kuće 11 ili veci.
[ X Files @ 27.01.2011. 12:03 ] @
Citat: Konstanta 3 nije ni potrebna [...]
Umesto:
"Koliko su stare tri kćerke?"
Treba da stoji:
"Koliko su stare kćerke?"
Tako?
[ atelago @ 27.01.2011. 12:40 ] @
Prevideo sam: 1229 i 1166 (Ova žena se stalno blizni!) ali ako postoje tri cerke onda moze biti
149 sto opet daje sumu 14
[Ovu poruku je menjao atelago dana 27.01.2011. u 14:04 GMT+1]
[ atelago @ 27.01.2011. 13:06 ] @
Prevideo sam: 1229 i 1166 (Ova žena se stalno blizni!)
Ako postoje tri cerke onda moze biti 149 sto opet daje zbir 14
tako da je jedino resenje ako su tri cerke
[ petarm @ 27.01.2011. 16:30 ] @
Citat: Sini82: Jel' ti mene zezaš, il' stvarno ne razumiješ? Kao da čitaš moje postove na pola, vadiš dijelove iz konteksta i citaraš ih. Poenta je da ako je student došao do jedinstvenog rješenja, dvije sestre moraju da budu blizankinje.
Zato što su onda rješenja (9,2,2) i (6,6,1) ravnopravna, student ne bi mogao da odredi koliko kćerke imaju godina (rješenje ne bi bilo jedinstveno). To ne dolazi u obzir, jer je poslednja informacija koju je dobio detalj koji je nedostajao da odredi koliko imaju godina. Dakle, rješenje postoji i jedinstveno je. Nameće se jedini mogući zaključak, da dvije sestre jesu blizankinje. Jasno je da onda najstarija kćerka ima 9 godina a druge dvije su blizankinje i imaju po 2 godine.
Nedeljko se ocito pita zasto iskljucujes mogucnost da je jedna sestra rodjena u januaru, a druga u decembru iste godine? One onda nisu bliznakinje, a imaju isto godina u nekom vremenskom intervalu! [ peka @ 25.05.2011. 02:04 ] @
Code:
Dato je 100 crnih kuglica, 100 belih kuglica i 2 kutije.
Prvo se nasumicno bira jedna kutija, a zatim iz te kutije nasumicno izvlaci jedna kuglica.
Rasporediti kuglice u kutije tako da verovatnoca da ce biti izvucna crna kuglica bude maksimalna.
Kolika je verovatnoca? [ vukadinovic.i @ 25.05.2011. 07:38 ] @
Pošto se kutija bira nasumično, to će max verovatnoća izvlačenja crne kuglice biti ako se u jednu kutiju stavi jedna crna kuglica, a u drugu kutiju ostale kuglice.
Tada je tražena verovatnoća:
P=1/2*1+1/2*99/199
[Ovu poruku je menjao vukadinovic.i dana 25.05.2011. u 09:10 GMT+1]
[ komb @ 30.07.2011. 09:37 ] @
Slavni majstor logičkih veština je tri svoja učenika ( koji se zovu A, B i C) stavio na test. Uzeo je 8 kugli: 4 crvene i 4 zelene. Svakom je dao po dve kugle i za sebe je zadržao dve. Svako od učenika je mogao da vidi kugle svojih drugara ali nije mogao da vidi svoje dve kugle niti dve kugle koje se nalaze kod učitelja. Učitelj postavlja pitanje osobi A: "Da li znaš koje su boje tvoje dve kugle"? Ukoliko učenik A ne zna odgovor tada on isto to pitanje postavlja drugom učeniku i tako dalje. Odgovori učenika su sledeći:
A: "Ne."
B: "Ne."
C: "Ne."
A: "Ne."
B: "Da!!"
Koje su kugle kod osobe B? Koje su kod osoba A i C? Koje se kugle nalaze kod učitelja ?
[ Nedeljko @ 04.08.2011. 16:21 ] @
Vazduh ipo za amper ipo pojede žuto ipo. Koliko žutog pojedu tri vazduha za tri ampera?
[ SrdjanR271 @ 04.08.2011. 19:59 ] @
Citat: Nedeljko: Vazduh ipo za amper ipo pojede žuto ipo. Koliko žutog pojedu tri vazduha za tri ampera?
Pojede žuto ipo... ahahahhaha, vrh. [ zzzz @ 05.08.2011. 12:10 ] @
Citat: SrdjanR271: Pojede žuto ipo... ahahahhaha, vrh.
Nekako sve asocira da je amper zapravo tuta,a vazduh je neugodnog mirisa i bučan.
Da bi se zadatak uozbiljio treba preimenovati objekte,naprimjer ovako:
1.5A za 1.5 B dobije 1.5 C
Koliko će dobiti 3A za 3B?
Ili ovako:
Kroz cijev prečnika 1.5 cm za 1.5 s isteče iz bureta 1.5 l vina.
Koliko vina će isteći kroz cijev prečnika 3 cm za 3 sekunde? [ Nedeljko @ 05.08.2011. 17:43 ] @
Citat: zzzz: Da bi se zadatak uozbiljio treba preimenovati objekte,naprimjer ovako:
1.5A za 1.5 B dobije 1.5 C
Koliko će dobiti 3A za 3B?
Moj zadatak je samo specijalan slučaj tvog. Ko reši tvoj, rešio je i moj. Ja sam savršeno ozbiljan. Evo i rešenja:
Vazduh ipo za amper ipo pojede žuto ipo.
Znači, vazduh ipo za jedan amper pojede jedno žuto.
Dakle, jedan vazduh za jedan amper pojede 2/3 žutog.
Dalje, tri vazduha za jedan amper pojedu dva žuta.
Konačno, tri vazduha za tri ampera pojedu šest žutih.
Šta nije u redu? [ zzzz @ 05.08.2011. 20:25 ] @
Citat: Nedeljko: Moj zadatak je samo specijalan slučaj tvog. Ko reši tvoj, rešio je i moj. Ja sam savršeno ozbiljan.
....Konačno, tri vazduha za tri ampera pojedu šest žutih.
Šta nije u redu?
Evo šta:
Kroz cijev prečnika 1.5 cm za 1.5 s isteče iz bureta 1.5 l vina.
Koliko vina će isteći kroz cijev prečnika 3 cm za 3 sekunde?
U ovom zadatku rješenje nije 6 litara već 12.To je zato što za dvostruko veći promjer imamo 4x veći protok jer je površina 4 puta veća.
Moguće je da amperi i žuti nisu u linearnoj relaciji jer bi vjerovatno došlo do izvjesnog zasićenja i usporenog jedenja..
[ atelago @ 09.08.2011. 18:41 ] @
Citat: zzzz: To je zato što za dvostruko veći promjer imamo 4x veći protok jer je površina 4 puta veća.
Ni stvarno ni teretski nije tako čak ni kod jednakog kvaliteta obrade provodnika i istog fluida. [ fentalijana @ 10.08.2011. 15:33 ] @
A sto niko ne resi zadatak koji je postavio komb?
[ zzzz @ 10.08.2011. 18:13 ] @
Citat: fentalijana: A sto niko ne resi zadatak koji je postavio komb?
U pravu si.Ajmo početi.
1)A je vidio da B i C nemaju četiri kugle iste boje.
2)B to shvata,ali gledajući kugle kod A i C nezna šta je kod njega.
--- idemo dalje polako. [ atelago @ 11.08.2011. 08:41 ] @
Možda bi moglo ovako

Na kraju treba da stoji: Svi imaju raznobojne kugle
[Ovu poruku je menjao atelago dana 11.08.2011. u 10:05 GMT+1][ vukadinovic.i @ 11.08.2011. 10:05 ] @
@atelago
Svaka cast za trud. Mislim da je pravo resenje ipak 2 slucaj. Cini mi se da se greska potkrala u ovoj recenici:
"Moje kugle nisu zelene jer bi B video dve crvene i dve zelene kugle i znao bi da njeove kugle nisu jednobojne kao ni L-ove, jer A i C se ne javljaju."
Problem je sto se C javlja nakon B, te B moze samo da zakljuci da njegove kugle nisu dve kugle iste boje kao boje kugli ucenika C.
Konacno resenje:
B i L kugle razlicitih boja
A dve kugle iste boje
C dve kugle iste boje, ali boje razlicite od A
[ atelago @ 11.08.2011. 12:31 ] @
Citat: vukadinovic.i:
Konacno resenje:
B i L kugle razlicitih boja
A dve kugle iste boje
C dve kugle iste boje, ali boje razlicite od A
Koji učenik je ovo zaključio i zašto?
[ vukadinovic.i @ 11.08.2011. 13:28 ] @
Ovo je zakljucio ucenik B, jer kao sto u zadatku pise, on prvi odgovara sa "Da!", na pitanje "Da li znas koje su boje tvoje kugle?"
[ zzzz @ 12.08.2011. 16:12 ] @
Citat: vukadinovic.i: Ovo je zakljucio ucenik B, jer kao sto u zadatku pise, on prvi odgovara sa "Da!", na pitanje "Da li znas koje su boje tvoje kugle?"
Ovo je u redu jer:
Raspodjela je mogla da se obavi samo na pet kombinacijskih načina:
1-tri raznobojna para.
2-dva raznobojna para,a jedan istobojni.
3-jedan raznobojni par a dva istobojna različite boje
4- jedan raznobojni par a dva istobojna iste boje.
5-Nijedan raznobojni par,sva tri istobojna.
Ova dva zadnja ne dolaze u obzir jer bi najdalje u trećem potezu došao potvrdan odgovor.
U slučaju 3 onaj sa raznobojnim parom bi mogao dati potvrdan odgovor ako su se prethodno druga dva sa jednobojnim parovima izjasnila negativno.Prema tome to nije ni C ni A.
Ostala dva slučaja ne mogu dati potvrdan odgovor.
[ anonimnistefi @ 16.04.2012. 03:24 ] @
Ne znam da li je 23 zadatak resem,ali nemam zivaca da prodjem kroz svih 42 stranica da saznam. Resenje moze biti funkcija ceo deo iz n/2 gde je n taj broj sam sto ce funkcija imati negarivan znak ako je n neparno a pozitivan znak ako je n parno.
[ zarkoj @ 21.09.2012. 11:08 ] @
Ne znam da li je ova tema jos aktivna ali evo jedan zadacic ;)
Vlada i Nada imaju odredjeni broj bombona. Kad Vlada da Nadi 10 imace podjednako. Ako Nada da Vladi 20 onda ce Vlada imati 4 puta vise bombona od Nade.
Koliko svako od njih ima bombona. :)
Mozda ovakav zadatak ima mozda nema........
[Ovu poruku je menjao zarkoj dana 22.09.2012. u 08:46 GMT+1]
[ berazorica @ 21.09.2012. 21:49 ] @
^ Koliko osoba je u zadatku? Blada, Hada, nada i Vlada? 
[ zarkoj @ 22.09.2012. 07:46 ] @
hahah sredjeno ;)
[ anonimnistefi @ 18.01.2013. 03:04 ] @
Vlada-60, Nada-40
[ miki069 @ 29.01.2013. 16:04 ] @
Ispade da je -80 veći broj od -20?
I to cela četiri puta.
[ berazorica @ 29.10.2013. 14:54 ] @
Zamalo da Društvu matematičara pošaljem rešenje zadatka o kom sam neko vreme razmišljala, a onda primetim da je zadatak predviđen za osnovce. Zaista, nema tu ničeg što se ne uči u osmom razredu, ali ipak bih podelila zadatak sa vama:
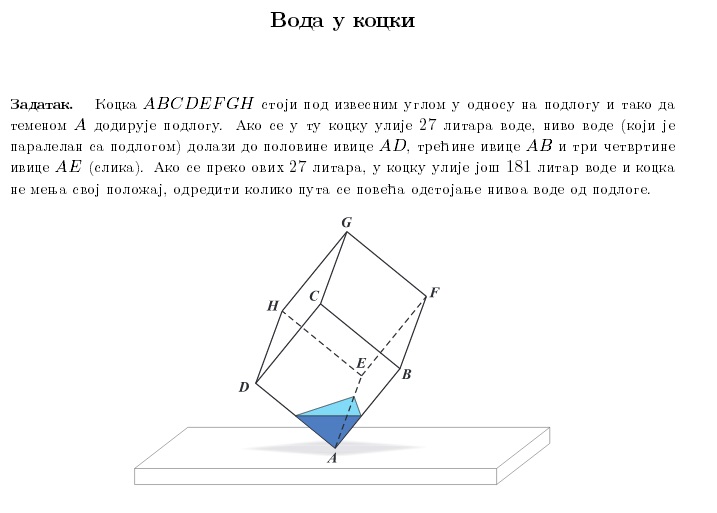
A ovaj zadatak je prelep, ali još uvek ga nisam rešila:
Svaka tačka ravni obojena je jednom od dve boje. Neka je ABC proizvoljan trougao. Dokazati da u toj ravni postoji trougao sličan trouglu ABC, kome su sva tri temena obojena istom bojom. [ number42 @ 29.10.2013. 16:07 ] @
ovo bi trebalo da je dirhelov princip... znaci ako je skup A veci od skupa B, on ne moze ceo da se preslika u njega vec uvek imamo visak. evo da pokusam:
ako farbamo zutom i plavom, pretpostavimo da zuto ofarbamo krug u koji moze da se smesti ceo trougao, tj sva temena trougla, a oko njega plavo.
ali dokazujemo suprotno da bi dobili kontradikciju, pa znaci izmestamo temena trougla van zutog kruga u plavu okolinu, tj farbamo manji krug od prvog. onda su sva temena van zutog kruga, ali su opet u plavoj oblasti- sva tri.
ovde sam simulirao jako pravilan raspored boja, ali sad je pitanje kako se ovo uopstava na nepravilno farbanje i nasumican raspored boja.
[ Bojan Basic @ 29.10.2013. 16:33 ] @
Citat: berazorica:
Svaka tačka ravni obojena je jednom od dve boje. Neka je ABC proizvoljan trougao. Dokazati da u toj ravni postoji trougao sličan trouglu ABC, kome su sva tri temena obojena istom bojom.
Pomoć: pretpostavimo suprotno (u želji da dobijemo kontradikciju). Dokazati najpre da, pod tom pretpostavkom, za svake dve tačke koje su obojene istom bojom središte duži koje one određuju mora biti obojeno suprotnom bojom. Zatim dokazati da je ovakvo bojenje nemoguće (za ovaj poslednji korak dovoljno je uzeti devet kolinearnih tačaka od kojih su svake dve susedne na jednakom rastojanju). [ berazorica @ 29.10.2013. 17:29 ] @
Dakle, pretpostavimo suprotno, tj. da svaki trougao u toj ravni koji je sličan trouglu ABC, ima dva temena jedne i jedno druge boje. Npr. posmatramo neki sličan trougao EFG, i neka su mu temena E i F crvena, a G plavo. Posmatramo onda središta stranica trougla i uočavamo da, ako bi središte stranice EF bilo crveno, onda nijedno od druga dva središta, ne bi smelo da bude crveno, jer bi sa središtem EF i jednim od temena E i F davalo sličan "jednobojan" trougao, a tada su oba plava, pa sa preostalim temenom G daju sličan plavi trougao. Znači, središte svake duži čiji su krajevi iste boje, mora biti druge boje.
Ako posmatramo predloženih devet kolinearnih tačaka, pokušavanjem bojenja po pravilu o središtu duži, dolazimo kod svih mogućih kombinacija do nemogućnosti da obojimo neku od šeste do devete tačke.
Ovaj pristup mi nikad ne bi pao na pamet, razmišljala sam u pravcu kreiranja neke figure sastavljene od sličnih trouglova, koja bi u svakoj kombinaciji boja davala traženi trougao.
Hvala, Bojane. Možda sam ovim zadacima pokvarila suštinu konkursa Društva, ali previše je vremena prošlo od marta.
[Ovu poruku je menjao berazorica dana 29.10.2013. u 19:04 GMT+1]
[ number42 @ 30.10.2013. 15:11 ] @
tu bi bilo zanimljivo pogledati sta se desava kada se trazi identican umesto slicnog trougla, i da li se moze dokazati da jeste ili nije moguce.
[ Bojan Basic @ 30.10.2013. 18:57 ] @
Nije tačno da se tada (u opštem slučaju) uvek može naći trougao s jednobojim temenima. Kontraprimer: neka je fiksiran jednakostraničan trougao stranice 1. Ravan podelimo na vertikalne trake širine 1, zatvorene s leve strane a otvorene s desne, i obojimo naizmenično. Pri ovakvom bojenju ne možemo naći jediničan jednakostraničan trougao čija su sva tri temena iste boje.
[ berazorica @ 30.10.2013. 21:17 ] @
Citat: Bojan Basic: Nije tačno da se tada (u opštem slučaju) uvek može naći trougao s jednobojim temenima. Kontraprimer: neka je fiksiran jednakostraničan trougao stranice 1. Ravan podelimo na vertikalne trake širine 1, zatvorene s leve strane a otvorene s desne, i obojimo naizmenično. Pri ovakvom bojenju ne možemo naći jediničan jednakostraničan trougao čija su sva tri temena iste boje.
Zar ne bi trebalo da su trake širine  ? [ Bojan Basic @ 30.10.2013. 21:30 ] @
Tačno, širine  . Zahvaljujem na ispravci. [ berazorica @ 31.10.2013. 06:53 ] @
Dok je još 2013. da probamo i ovo:
 [ berazorica @ 13.11.2013. 14:13 ] @
Niko nema vremena/volje da se pozabavi ovim zadatkom? Meni se baš dopada, ali nisam daleko odmakla u rešavanju. Zaključci do kojih se lako dolazi su sledeći:
- 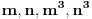 imaju iste ostatke pri deljenju sa 3
- ako je 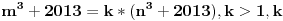 prirodan broj
onda 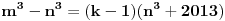 .......................... (*)
tj. 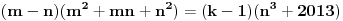 ,
pa kako 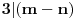
i 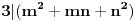
sledi da 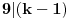 ili 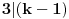 i 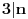 .
S obzirom na (*), i da svakako 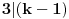 , znamo da 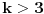 , te da je 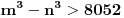 , možda možemo da posmatramo prvih nekoliko desetina kubova i donesemo zaključak... Ili ovo nije ni blizu pravog načina razmišljanja? [ Sini82 @ 13.11.2013. 20:12 ] @
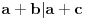 je ekvivalentno sa 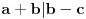 (lako se provjeri).
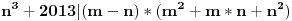 .
Pretpostavimo da 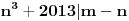 tj. 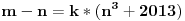 , gdje 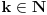 .
Dobijamo da vrijedi 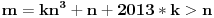 .
Dakle za svako n postoji 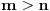 tako da vrijedi tvrdjenje pod a). [ berazorica @ 14.11.2013. 06:04 ] @
Lepo!
Ja sam imala skroz pogrešan prilaz, jer sam očekivala da ću doći do nekog gornjeg ograničenja i konačnog skupa rešenja.
[ Forzgov @ 31.01.2014. 16:22 ] @
Idu dva kamiona jedan za drugim. Onaj oprednji ide ide pa stane, a onda iz njega iziđe vozač sa nekom močugom i počne da lupa po karoseriji i onda se opet vrati u kabinu i krene dalje, ali posle izvesnog vremena dogodi se opet to isto. Pošto se to često ponavljalo onda vozač iz zadnjeg kamiona upita vozača prednjeg kamiona šta se dešava. Ovaj mu odgovori da vozi nešto što mu spušta karoseriju na točkove i zakoči ih.
Šta je vozio?
[ RMAN @ 03.05.2014. 16:10 ] @
Slona  [ Typo @ 17.09.2014. 00:54 ] @
Evo ja imam jedan lepi, ali ni sam nisam siguran u rješenje.
Zadan je niz od n znakova. Taj niz podelite na pomicne prozore duljine k.
Za svaki znak u nizu imate verovatnoću pogreške p.
Za zadane parametre p, k i n potrebno je odrediti očekivanje i varijancu broja pomičnih prozora bez ijedne greške.
Samo kratka napomena oko pomičnog prozora. Ako je n = 5, a k=2, tada pomični prozor izdvaja članove stringa s indeksima 12, 23, 34 i 45.
[ miki069 @ 17.09.2014. 01:05 ] @
Ja nisam siguran ni u tekst zadatka.
1. Svi znakovi imaju istu verovatnoću greške p?
2. Slučajna promenljiva opisuje broj prozora sa nula grešaka?
2. Varijanca je disperzija ili devijacija?
[ Typo @ 17.09.2014. 12:38 ] @
1. Dakle, svaki znak u stringu ima verovatnost p da je pogrešan (i taj p je isti za svaki znak u stringu).
2.Slučajnu promenjivu treba definirati na neki način... Ja sam probao baš tako da opisuje broj prozora bez greške, ali onda treba ozračunati verovatnosti da takvih prozora ima 0 ili 1 ili 2 ili .... n-k+1, a kad se to krene računati ispadne dosta složeno.
Primerice za n = 3 i k = 2 lako se vidi da broj prozora bez grške uvelike ovisi o "geometriji" grešaka.
3. Disperzija u smislu Var(X) = E(X^2) - E(X)^2.
Imam osjećaj da bi to mogao biti neki trik u pitanju?
Također mi je poznato daje ovo jedan tipova problema koji se javljaju u teoriji kompleksih mreža.
[ miki069 @ 18.09.2014. 06:50 ] @
Misliš disperzija u smislu:
Var(X) = E((X - E(X))^2).
Obrazac:
Var(X) = E(X^2) - E(X)^2.
Nastaje razvijanjem kvdarata binoma u gornjem obrascu.
Praktičniji je za upotrebu, ali se u njemu ne vidi smisao disperzije.
Nebitno za problem.
[ Dzinaa @ 18.11.2015. 20:16 ] @
ZADATA IQ- XXX
Zbir dva prirodna broja, oba veca od 1 i manja od 50, poznat je osobi A, a njihov proizvod osobi B.
Oni vode ovakav razgovor.
Osoba A: “Ni ti ni ja ne znamo o kojim se brojevima radi”
Osoba B: “ U pravu si, ne znam brojeve”
Osoba A: “Ja ih jos uvek ne znam”
Osoba B: “Ja sada znam”
Osoba A: “I ja sada znam”
Koji brojevi su u pitanju?
Obrazloziti.
[ Dzinaa @ 18.11.2015. 20:18 ] @
ZADATA IQ- XXX
Zbir dva prirodna broja, oba veca od 1 i manja od 50, poznat je osobi A, a njihov proizvod osobi B.
Oni vode ovakav razgovor.
Osoba A: “Ni ti ni ja ne znamo o kojim se brojevima radi”
Osoba B: “ U pravu si, ne znam brojeve”
Osoba A: “Ja ih jos uvek ne znam”
Osoba B: “Ja sada znam”
Osoba A: “I ja sada znam”
Koji brojevi su u pitanju?
Obrazloziti.
[ zzzz @ 19.11.2015. 23:16 ] @
To je već bilo na ovom forumu. Pogledaj..
Copyright (C) 2001-2024 by www.elitesecurity.org. All rights reserved.
|