|
|
[ darkosos @ 05.09.2003. 09:12 ] @
|
| Zadatak, preuzet iz najnovijeg 'Zabavnik'-a, uproscen :
Svih 120 stanovnika nekog mesta je otislo na koncert i ostavilo na kasi ukupno 120€. Karta za muskarce je kostala 5€ (polna diskriminacija), za zene 2€ i za decu 0.1€ (10 centavosa). Pitanje je naravno demografsko, o strukturi stanovnistva.
Naravno, posle malo nabadanja, resenje nije toliko tesko naci. Ali me je usput zainteresovalo sledece. Na primer, resavajuci ovaj zadatak, mozemo naici na sledecu jednacinu :
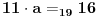
Odnosno trazi se broj koji, pomnozen sa 11, daje ostatak 16 posle deljenja sa 19. Koje su tehnike resavanja ovakve jednacine? Posle malo razmisljanja, dosao sam na ideju o deljenju po modulu, tj. nesto kao :
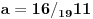
Stvarno ne znam da li ovo postoji negde u literaturi, znam samo da nigde nisam video da se to pominje. U svakom slucaju, da bi ovo bilo izvodljivo, mora postojati (jedinstven) inverzni element za mnozenje u skupu modula. Cini mi se da je dovoljno da uzmemo skup modula nekog prostog broja, sto je ovde zadovoljeno.
Dakle, ako postoji inverz, 11-1, onda je resenje
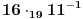
Tehnikom 'corave koke' moze se videti da je resenje a=17, kao i da je inverz za 11 jednak 7 (7*11 = 77 = 4*19 + 1). E sad, kada bismo mogli da prvo izracunamo inverz i zaobidjemo coravu koku, resenje bi dobili ovako : 16*7 = 112 = 17 (mod 19).
Zna li neko kako se efektivno moze naci ovakav inverzni element? (no blind chikens, please). Imam neku ideju, ali jos nisam realizovao. |
[ zzzz @ 05.09.2003. 09:55 ] @
Znam ja odličnu metodu koju sam razvijao čisto iz dosade 91-95 god.I kad sam mislio da sam jako pametan , nađem u nekoj knjižici da je to već izmislio Euklid prije
više od 2000 god.Ja sam zapravo rješavao zadatak Dejana Ristanovića iz Galaksije:
nađi 10-to cifren broj , koji kad se kvadrira ima zadnjih 10 cifara istih kao i početni broj.Takođe i onaj zadatak što je riješio Petrae.Zadani ostaci pri djeljenju sa 3,5,7
treba naći koji je to broj.Moram raditi pa ću objašnjenje dati na veče.
[ darkosos @ 05.09.2003. 12:52 ] @
Malo sam listao neke knjige iz algebre i nasao dve bitne stvari :
- Ako je p prost broj, tada je Z p polje (tj. postoji inverz za mnozenje)
- Fermaova teorema : ako su n i p uzajamno prosti i p prost, tada je
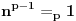
Odatle bi sledilo da je
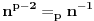
sto daje ono sto sam trazio, ali nije bas najefikasnije, posebno za velike brojeve. [ zzzz @ 05.09.2003. 23:24 ] @
Ovako se može riješiti lin. jednačina sa 2 cjelobrojne nepoznate ako su i koeficijenti
i slobodni član cijeli brojevi.
ax+by=c Riješimo ax+by=1 , pa rješenja pomnožimo sa c.(a i b moraju biti relativno prosti , ili i c mora sadržati njihov zajednički faktor.
Ako nađemo par rješenja onda imamo beskonačno mnogo parova.x(i)=x(1)+i*b ;
y(i)=y(1)-i*a ." i " je cijeli broj.
Osnovna ideja rješavanja je redukcija faktora.Pogledajmo ovu jednačinu:
(a-b)m+bn=1 (prosto rečeno veći koeficijent umanjim manjim i dobijem lakši
zadatak.Kad bi sad izračunali nepoznate m i n mogli bi naći i x i y.Evo kako:
am+b(n-m)=1 odavde poređenjem x=m;y=n-x.
Možemo redukovati i žešće. I=Int(a/b) , pa je (a-I*b)x+bn=1 Rekurzija:y=n-I*x
Možemo ovu redukciju primjeniti višestruko sve dok ne dođemo do trivijalno jednostavne jednačine koju riješimo , a zatim se rekurzijom vratimo do osnovne jednačine.
Radi preglednosti napisaću osnovnu jednačinu malo drukčije:a(1)x(2)+a(2)x(1)=1.
(broj u zagradi je indeks)
a(3)=a(1)-I(1)*a(2) ;I(1)=Int(a(1)/a(2)); x(1)=x(3)-I(1)*x(2)
---------
a(i+2)=a(i)-I(i)*a(i+1);I(i)=Int(a(i)/a(i+1); x(i)=x(i+2)-I(i)*x(i+1)
Tjeramo redukciju sve dok ne dobijemo a(n)=1 , a zatim riješimo ovo:
a(n-1)x(n)+1*x(n-1)=1. Očigledno da možemo uzeti x(n)=0;x(n-1)=1
Slijedi rekurzija unatrag i dobijamo osnovno rješenje , a iz tog para i sva ostala moguća.
Napomena:Namjerno nisam komplikovao priču sa negativnim brojevima da bi lakše
istakao ideju .Evo jednog primjera u sledećoj poruci:
[ zzzz @ 06.09.2003. 00:15 ] @
U jednoj Galaksiji sam našao ovakav zadatak od Dejana Ristanovića:
Nađi desetocifren broj koji kad se kvadrira zadnjih 10 cifara je upravo taj broj.
(Mislim da nije bio 10 cifreni već pet-šest ali nema veze).
x^2=m*10^10+x
x*(x-1)=p*q*5^10*2^10
-------------------------
x=p*5^10
x-1=q*2^10 (ima i ono drugo rješenje ali nećemo se sad njime baviti)
--------------
p*5^10-q*2^10=1 nađimo ove 2 nepoznate.
ovu jednačinu napišem ovako: 9765625*x(2)-1024x(1)=1
i a(i) I(i) x(i)
--------------------------------------
1¸¸¸¸¸9765625¸¸¸¸¸¸-9375 ¸¸¸¸¸¸-1745224
2¸¸¸¸¸¸¸- 1024 ¸¸¸¸¸¸¸¸3 ¸¸¸¸¸¸¸¸¸¸-183
3 ¸¸¸¸¸¸ -263 ¸¸¸¸¸¸¸¸¸¸1 ¸¸¸¸¸¸¸¸¸¸¸¸47
4 ¸¸¸¸¸¸ -235 ¸¸¸¸¸¸¸¸¸¸8 ¸¸¸¸¸¸¸¸¸¸¸¸-42
5 ¸¸¸¸¸¸-28 ¸¸¸¸¸¸¸¸¸¸¸¸2¸¸¸¸¸¸¸¸¸¸¸¸¸¸5
6 ¸¸¸¸¸¸-11 ¸¸¸¸¸¸¸¸¸¸¸¸1 ¸¸¸¸¸¸¸¸¸¸¸¸¸-2
7 ¸¸¸¸¸¸ -6 ¸¸¸¸¸¸¸¸¸¸¸¸1 ¸¸¸¸¸¸¸¸¸¸¸¸¸¸1
8 ¸¸¸¸¸¸¸-5 ¸¸¸¸¸¸¸¸¸¸¸¸¸¸¸¸¸¸¸¸¸¸¸¸¸¸-1
9 ¸¸¸¸¸¸¸-1 ¸¸¸¸¸¸¸¸¸¸¸¸¸¸¸¸¸¸¸¸¸¸¸¸¸¸ 0
--------------------------------------------
Nakon redukcije imam ovu jednačinu: -5*x(9)-1*x(8)=1.Odatle rješenja 0;-1
prikazana na dnu desne kolone.Rekurzijom idem do vrha desne kolone.
Rješenja su na vrhu ali negativna.Nađemo najmanji pozitivan par:
x(1)+a(1)=80204001;x(2)+a(2)=841
traženi broj je 841*5^10=8212890625.
Moglo je i 8020401*2^10+1
Za rješavanje ovom metodom dobro dođe kalkulator i oprez sa predznacima!
[ darkosos @ 07.09.2003. 08:00 ] @
Hm da, ta rekurzija....
Nije mi bas najjasnije na kraju, oko izbora resenja. Evo kako sam ja to shvatio, na onom pocetnom primeru :
11x - 19y = 1
11x - (11+8)y = 1
11(x-y) - 8y = 1 i dalje, u istom fazonu
8(x-2y) + 3(x-y) = 3(2x-3y) + 5(x-2y) =
3(3x-5y) + 2(x-2y) = 2(4x-7y) + (3x-5y) = 1
Ako izberemo x=7, y=4, zaista se dobija resenje za pocetnu jednacinu, odnosno ono sto mene vise interesuje, inverz za 11 - to je 7. Ali sam probao slicnim rezonom i sa nekim drugim brojevima, pa mi je nesto bilo cudno. Dosao sam opet do koeficijenata 2,1, a resenje nije odgovaralo, kada napravim isti izbor (dobio sam -1).
Metoda koju si prikazao je nesumnjivo mocna, posebno sa brzom redukcijom. Ja bih ipak nekako voleo da je 11-1 =19 f(11,19), a f nije rekurzivna funkcija :)
[ zzzz @ 07.09.2003. 14:53 ] @
Rješenje zadatka iz Zabavnika: m+n+p=120 ;5m+2n+0.1p=120
Smjenom p=120-m-n dobijem 49m+19n=1080
Rješim jednadžbu 49*x2+19*x1=1
ai €€€ Ii €€€ xi
------------------
49 €€€ 2 €€ -18
19 €€€ 1 €€€ 7
11 €€€ 1 €€ -4
8 €€€€2 €€ 3
3 €€€€ 1 €€ -1
2 €€€€€€€€ 1
1 €€€€€€€€ 0
---------------------
m=7*1080-i*19
n=(-18)*1080+i*49
Nađem " i" da bi rješenja bila pozitivna: i=Int(7*1080/19)=397.
odavde m=17;n=13; p=120-17-13=90
------------------------------------------------------------------
Zašto sam odabrao x7=0 i x6=1 ? , iz jednačine 2*x7+1*x6=1
Pa mogao sam uzeti naprimjer da je x7=4;x6=-7
Tada bi rekurzija treće kolone odozdo išla:4;-7;11;-29;40;-69;178 umjesto
o;1;-1;3;-4;7;-18
Rješenja :m=1080*(-69)+i1*19
n=1080*178-i1*49
Za i1=3923 slijedi m=17; n=13 .(Dakle isto samo kabastiji brojevi)
Zato je najracionalnije poslednji "xn" uzeti da je nula a sledeći 1 , ili -1 (ovisi o
zadatku)
Ovo sa inverz metodom koju pokušavaš uobličiti nisam razumio.Moram pažljivije pročitati.
[ darkosos @ 08.09.2003. 09:59 ] @
Da, resenje je (17,13,90). Bas ih se nakotilo :)
Sinoc sam celo vece sa kumom lupao glavu oko tog inverza, pa i od jutros - ne da mi mira. Mada evo jedne dosetke za konkretan slucaj.
Umesto za 11, mozemo da potrazimo inverz za 19-11=8, pa onda dodamo minus (laka je provera da je ovo ok).
Posto je 8 = 2 3, a 2 -1 = 19 10 (to je najlaksi inverz; dakle uvek je 2 -1 = p [p/2]+1 ), imamo da je
8 -1 = 19 10 3 = 1000 = 19 12 i konacno
11 -1 = 19 -12 = 19 7.
I kratak dokaz za ono sa minusom :
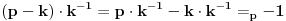 [ darkosos @ 09.09.2003. 08:28 ] @
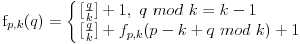
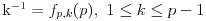
Jos jedna ideja stize uskoro.
[ Ovu poruku je menjao darkosos dana 09.09.2003. u 20:14 GMT] [ zzzz @ 09.09.2003. 14:00 ] @
Ako sam dobro razumio.
Jednačina na samom početku je izašla iz 30*a-19*c=-1200 ,a odatle
11*a+19(a-c)=-1200.
16 si dobio kao (-1200)Mod(19)=16.Jesam li dobro shvatio?
Sada si imao problem kako naći inverz 11 u (jednom potezu) na polju 19.
INV(11)*11=x*19+1 (Da li se dobro izražavam?)
Zaključio si da je to teško kad bi se radilo o većim brojevima pa si uveo još jednu
redukciju (8).Tu je bilo malo problema i diskusije oko predznaka (-).
Ovo mi jako liči na redukciju:30;19;11;8;3;2;1
Samo pronalaženje INV(n) je rješavanje istog tipa jednačine kao na samom početku
pa se nameće da nastavimo istim postupkom dalje , a to je onda rekurzivna metoda.
Pokušaj još , možda nešto ispadne , ali ja tu ne vidim neku šansu.
Uskoro ću dati rješenje jednog interesantnog zadatka pomoću rekurzivne metode.
Takođe i malo precizniji opis rekurzivnog postupka.
[ darkosos @ 09.09.2003. 18:31 ] @
Da, dobro su razumeo zzzz. Sve krece od
(a,b) = 1 sledi postoje x, y tdj. ax + by = 1.
Ali meni ne treba y, vec samo x jer je to inverz za a u polju Z b.
I izgleda za zaista nema bega od rekurzije; evo jos jednog resenja :
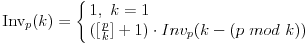
Obrazlozenje je sledece :
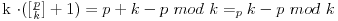
Evo primera, da ne bude suvise apstraktno :
p = 113, k=5 ; 113 = 22*5 + 3
[113/5] + 1 = 23
5*23 = 113 5 - 3 = 2
Ovu jednacinu sada mnozimo sa 2 -1 :
5*(23*2 -1) = 113 1
Copyright (C) 2001-2024 by www.elitesecurity.org. All rights reserved.
|