|
|
[ Meffisto123 @ 03.04.2004. 22:14 ] @
|
| Evo niza:
12,27,167,4015,...
Evo male pomoci,to je broj:******
Ko ga resi ima pivo ! ! !
|
[ stalker @ 04.04.2004. 15:26 ] @
Da li moze pomoc? Ima li niz IKAKVE veze sa stepenom dvojke i uopste stepenima?
[ soma @ 05.04.2004. 09:47 ] @
Daj malu pomoc neide ovako pjeske!!!
[ DDMM @ 05.04.2004. 11:26 ] @
Takvi zadaci spadaju u klasu zadataka kojima se ispituje odraslost inteligencije kod dece.
Secam se jedne pricice iz matematickog listica koji prica pricu o nekom super-pametnom klincu koji celom razredu dokazuje da sledeci broj od niza brojeva 1,2,3,4,5 moze biti 7. A onda kasnije nastavlja pricu i kaze da moze namestiti bilo koji broj.
Da bi takav niz imao "smisla" uzastopne razlike odgovarajuceg nivoa bi trebale da budu nule. Kod primera 1,2,3,4,5 prvi nivo razlika je 1,1,1,1 drugi 0,0,0 pa kad se vrati nazad "lepo" dobijemo 6. Kod testerastih nizova mozemo smisliti nesto sto ima slicnu "logiku".
Jos jedna primena bi mogla biti u parapsihologiji.
Procitajte misli onom ko je izmislio zadatak.
E, to je vec nesto ozbiljnije.
[ Nedeljko @ 06.04.2004. 12:37 ] @
Neka mi neko produži ovaj niz
1,2,3,4,5
Sledeći član može da bude bilo koje m jer je niz 1,2,3,4,5,m početni deo niza sa opštim članom:
a_n = n + (n-1)(n-2)(n-3)(n-4)(n-5)*m/120.
Drugim rečima, ovakvi zadaci NIKADA nemaju smisla jer je svaki broj rešenje koliko i bilo koji drugi. Ne sumnjam da će se neko naći da objavi formulu u koju će ovo da se uklopi, ali taj neće moći da obrazloži jedinstvenost tog rešenja, jer postoji beskonačno mnogo "pravilnih" nizova koji počinju kao bilo koji unapred zadat konačan niz, na primer ovaj iz zadatka.
[ chupcko @ 06.04.2004. 22:30 ] @
Nedeljko, ne da si u pravu, nego razbijas. Eto da su samo uspeli da se sete da kazu: trazimo broj koji nastavlja niz a da se moze izracunati u sto manje koraka (naravno treba se opredeliti za neki formalizam izracunavanja, ja predlazem URM, dakle trazi se program (formula po tezi churca) koja u sto manje koraka izracunava n-ti element.
u tom smislu bi program koji za 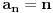 imao jednu instrukciju :).
Nedeljko, mislim da trazis '[','t','e','x',']' ... '[','/','t','e','x',']'. [ BluesRocker @ 08.04.2004. 14:08 ] @
Ljudi, i meni je jasno da je niz samo funkcija u diskretnom sistemu i da se kroz konacan broj tacaka moze provuci beskonacan broj razlicitih funkcija koje su sve odredjene nekim pravilom, pa su sve aproksimacije besmislene. Ali posto sam poznati pivopija ipak cu pokusati da dam odgovor, odnosno da pogodim sta je autor hteo da kaze. Moje resenje bilo bi broj 670674, pa sad ako je dovoljno za pivo...
[ VRider @ 08.04.2004. 14:22 ] @
Kako si dosao do tog broja?
[ BluesRocker @ 08.04.2004. 18:25 ] @
Nemam pojma. Malo mnozenja, oduzimanja, sabiranja, onako iz glave. A kako mi se cini, autor ni ne misli da se javi, da kaze da li je neko pogodio. Mozda je samo lupio 4 broja i ostavio nas da se nerviramo.
Bojan Bašić: obrisan nepotreban citat
[ Bojan Basic @ 08.04.2004. 22:13 ] @
Citat: Nedeljko:
Neka mi neko produži ovaj niz
1,2,3,4,5
Sledeći član može da bude bilo koje m jer je niz 1,2,3,4,5,m početni deo niza sa opštim članom:
a_n = n + (n-1)(n-2)(n-3)(n-4)(n-5)*m/120.
Uh, nešto si debelo pobrkao, ova formula je daleko od tačne, kako si zaključio da za a 6 ova funkcija ima vrednost m? Čini mi se da treba a n = n + (n-1)(n-2)(n-3)(n-4)(n-5)*(m-n)/120, mada možda ni ovo nije tačno. [ Nedeljko @ 08.04.2004. 23:51 ] @
Da, pogrešio sam. Treba da bude
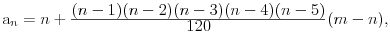
a može i
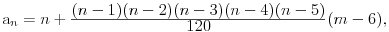
samo ne znam odakle ti ideja da ova formula nije tačna?
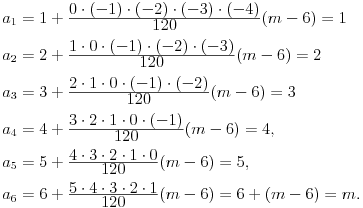 [ Bojan Basic @ 08.04.2004. 23:56 ] @
Nismo se razumeli, rekao sam da formula koju si malopre naveo (an = n + (n-1)(n-2)(n-3)(n-4)(n-5)*m/120) nije tačna, dok obe popravljene (ona na koju sam ja ukazao i ova druga koju si sad napisao) jesu.
[ Nedeljko @ 09.04.2004. 01:24 ] @
Bojane, podsećam te da si napisao "mada možda ni ovo nije tačno".
[ Bojan Basic @ 09.04.2004. 12:17 ] @
Dobro, dobro, to sam napisao zato što nisam kontrolisao formulu nego sam ja samo napisao napamet, iz glave, ali pošto si je ti proverio sad se slažemo da jeste tačna.
[ -zombie- @ 22.06.2004. 10:46 ] @
Citat: Nedeljko:
Neka mi neko produži ovaj niz
1,2,3,4,5
Sledeći član može da bude bilo koje m jer je niz 1,2,3,4,5,m početni deo niza sa opštim članom:
a_n = n + (n-1)(n-2)(n-3)(n-4)(n-5)*m/120.
Drugim rečima, ovakvi zadaci NIKADA nemaju smisla jer je svaki broj rešenje koliko i bilo koji drugi. Ne sumnjam da će se neko naći da objavi formulu u koju će ovo da se uklopi, ali taj neće moći da obrazloži jedinstvenost tog rešenja, jer postoji beskonačno mnogo "pravilnih" nizova koji počinju kao bilo koji unapred zadat konačan niz, na primer ovaj iz zadatka.
a šta ako zadatak glasi "produži niz čiji je opšti član definisan rekurentnom formulom" (dobro, ako ga i nisam precizno sročio, shvatili ste poJentu).
da li je tada isto tako moguće nastaviti svaki niz proizvoljnim članom. sve mi se čini da može, ali mi fali matematički aparat da to i pokažem.. ;) [ Bojan Basic @ 22.06.2004. 13:35 ] @
Nisam siguran da shvatam. Ako ti je dato prvih par članova a sledeći se dobija rekurentnom formulom od nekog ranijeg, onda je niz jedinstven, samo ideš redom i računaš jedan po jedan član. Ako si mislio nešto drugo, bitno je da od rekurentne možeš da dobiješ opštu formulu, i onda radiš sa tim ako ti više odgovara.
[ -zombie- @ 22.06.2004. 22:23 ] @
pa ovako, nedeljko je pokazao da je moguće svaki zadatak koji počinje sa "nastavi niz" rešiti tako što bi se dao opšti član niza an = f(n). ja pitam da li je moguće uraditi isto, samo što bi formula za opšti član niza bila u rekurentnom obliku, tipa an = x*an-1+y*an-2.
ili ako bi zadatak glasio ovako: dat je niz od n (recimo 5) članova, i počev od nekog (recimo trećeg), svaki član se dobija po nekoj formuli u odnosu na prethodnih m članova. pronađi tu formulu, i pronađi sledeći član niza..
(ovo sve naravno baš zato što se u tom duhu obično i postavljaju ovakvi zadaci, tj "traženo" rešenje je uvek u rekurentnom obliku..)
[ Nedeljko @ 22.06.2004. 22:50 ] @
Ja sam samo tvrdio da se na osnovu datih konačno mnogo članova beskonačnog niza ne može ništa zaključiti o preostalim članovima tog niza. Ukoliko ti zadaš rekurentne formule, onda si na taj način u potpunosti definisao jedan niz, pa onda tu više nema mrdanja. Dakle, Bojan je u pravu.
[ Bojan Basic @ 22.06.2004. 23:06 ] @
-Zombie, ja sam sad shvatio na šta misliš, na prvi pogled ne mogu da dam odgovor ali mi pitanje deluje zanimljivo. Da pojasnim:
Imamo prvih nekoliko članova nekog niza, neka bude npr. 1, 2, 3, 4, 5, i treba ovaj niz produžiti. Nedeljko je rekao da bilo koji broj može biti sledeći član niza, jer ako na sledeće mesto ubacimo proizvoljno m dobijamo niz čiji je opšti član
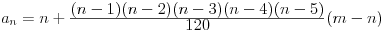
ili
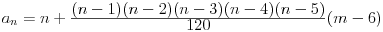 .
-Zombie- je postavio (veoma zanimljivo) pitanje, da li neki (npr. ovaj) niz možemo nastaviti bilo kojim brojem, ali tako da je opšta formula zapravo rekurentna. Opet sam loše objasnio, znači ovako: ako je sledeći član tog niza broj m, i niz je definisan nekom rekurentnom formulom (koju treba da pronađemo), da li za svako m možemo naći takvu rekurentnu formulu? [ Nedeljko @ 22.06.2004. 23:48 ] @
Naravno da može. Zavisnost se uvek može naći u obliku 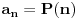 za neki polinom 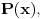 a svaki polinom se može zadati rekurentnom formulom. Recimo, ako je polinom 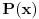 recimo stepena 4 i vodeći koeficijent mu je 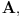 onda on zadovoljava jednačinu
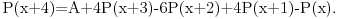
U opštem slučaju bi se koristili binomni koeficijenti. [ -zombie- @ 24.06.2004. 01:53 ] @
uh, mislim da nije to -- to.
ako nekome još nije jasno zašto sam ovo pitao, da objasnim. meni se čini da su svi takvi zadaci postavljeni u duhu da se nađe rekurentna zavistnost između članova.
to znači da se ta zavisnost može pročitati i na osnovu već datih članova niza. tj, recimo bar poslednja dva data člana moraju da zadovoljavaju rekurentnu formulu.
rešenje koje si ti nedeljko dao nije "u duhu" u kome su ti zadaci postavljeni, jer tvoju formulu zadovoljava tek sledeći element niza (koji nije dat, tj koji tek treba izračunati).
(bojane, ako ni ovo nisam dobro objasnio, slobodno možeš da probaš da to učiniš na razumljiviji način.. tebi to bolje ide nego meni ;)
[ Nedeljko @ 24.06.2004. 07:27 ] @
Evo, ovako. Pogodi koji sam ja niz zamislio. Jedina informacija je da se može rekurentno zadati i da je beskonačan. Ajd sad da te vidim. Tvoj zadatak ima smisla koliko i moj. Ili ako više voliš, nastavi niz 1,2,... Uostalom ko god da nastavi tvoj niz na bar jedan način koji nije isklučen u formulaciji zadatka rešio je zadatak. To što si ti zamislio neki drugi niz je isključivo tvoj problem. Postoji beskonačno mnogo nizova koji ispunjavaju tražene uslove.
Takav zadatak bi eventualno imao smisla ako bi se tražio najjednostavniji niz koji ispunjava tražene uslove, pri čemu bi morao u formulaciji precizno dadefinišeš pojam složenosti niza, tj. kada neki niz smatraš jednostavnijim od nekog drugog. Ne možeš ni taj posao da prepustiš rešavaču, jer bi to bilo isto kao da tražiš da neko reši zadatak koji si zamislio, bez da mu ga saopštiš.
P.S. U mom prethodnom postu bi u navedenoj formuli umesto A trebalo da stoji 24A.
[ srki @ 24.06.2004. 09:00 ] @
Zombie, trazis nesto ovako:
0 1 1 2 3 5 ?
ako posmatras kao Fibonacijev niz onda je sledeca vrednost 8.
Ali ako stavis an=(an-1-an-2+1)*an-2+1 onda ce sledeca vrednost biti 10. Sest prvih clanova je isto a sedmi nije.
[ -zombie- @ 24.06.2004. 23:24 ] @
upravo! odličan primer! ipak neko razume moje brbljanje.. ;)
e sad, pitam uopšteno.. da li je za svaki ovako zadati niz moguće naći bar dva različita rešenja, tj bar dve (različite) rekurentne formule koje zadovoljavaju ove uslove..
[ Bojan Basic @ 24.06.2004. 23:40 ] @
OK, -zombie-, deluje mi da sam ukapirao šta hoćeš (mada priznaj da nije bilo baš jednostavno na osnovu tvojih postova  ), pa bih te upitao za još neke detalje.
1) Da li rekurentna formula sme da uključuje samo 2 prethodna člana, ili može da zavisi i od više;
2) Da li članovi moraju da idu "redom" ili može i "na preskok (primer: recimo prva 3 su prozvoljna, 4=1+2, 5=2+3, 6=3+4 itd... gde se brojke naravno odnose na redni broj člana);
3) Kog oblika sve može da bude rekurentna formula (npr. eksponencijalna?);
4) i, ono najbitnije, koliko članova već zadatog niza mora da ispunjava rekurentnu formulu (u srkijevom primeru to su 4 člana), i da li taj broj zavisi od broja zadatih članova ili hoćeš neku konstantu?
Kad budeš odgovarao na ova pitanja, molim te idi po rednim brojevima  [ -zombie- @ 25.06.2004. 00:23 ] @
ma znam da nije jednostavno.. čak si i ti (kada si me razumeo), u prethodnoj poruci probao to da objasniš na dva različita načina.. ;)
elem, ovo nije neki "moj zadatak", pa da ja određujem pravila. ja samo pokušavam da zajedno (matematički) definišemo tačno ovakve zadatke koji se obično daju na nekim "testovima inteligencije", i da pokažemo da nemaju mnogo smisla..
dakle, ovo su samo moji predlozi..
1) koliko god
2) naravno (i to je najobičnija rekurentna formula)
3) bilo kog oblika, mada me prvenstveno zanimaju "prostija" rešenja (bez stroge definicije šta je "prostije", ali to je ionako samo preferencijal ;)
4) za ovo poslednje stvarno ne znam gde da postavim granicu. ;)
idealno rešenje (kao ovo što je dao srki) bi bilo da ako formula zavisi od prethodna dva člana, svi sem prva dva člana zadovoljavaju rekurentnu formulu (i fibonačijevu i onu drugu).
mislim da bi to baš bilo u duhu takvih zadataka, ali naravno, ako nema takvog rešenja, zanima me postojanje bilo kakvog (minimum je ipak dva, jer ispod toga nema smisla).
[ Nedeljko @ 25.06.2004. 09:43 ] @
Evo, niz 1,2,3,4,5 može da se produži kao
1,2,3,4,5,6,7,8,9,10,... 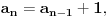 za 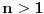 i 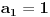
ili kao
1,2,3,4,5,6,7,8,1,1,1,1,1,... 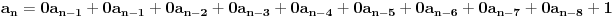 , za 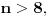 pri čemu je prvih osam članova dato.
ili kao
1,2,3,4,5,6,7,8,1,2,3,4,5,6,7,8,1,2,3,4,5,6,7,8,... 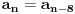 za 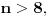 gde je takođe prvih osam članova dato.
Treba samo pustiti mašti na volju. [ Bojan Basic @ 25.06.2004. 13:25 ] @
Eureka!!!
Mislim da imam nešto što podseća na rešenje zadatka, nije baš opšti slučaj ali može da posluži kao početak. Elem, zaključak je:
Ukoliko je zadato prvih n članova niza niz možemo nastaviti na beskonačno mnogo načina ukoliko rekurentna formula obuhvata bar polovinu zadatih članova.
Najjednostavniji primer bi bio niz sa zadata prva 4 člana, opšta formula može biti:
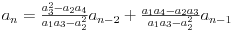
ili
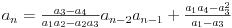
Mogu naći još sličnih formula, ako nekom zatreba neka kaže. Uglavnom, i za niz sa više članova mogu napisati dokaz za onu tvrdnju od malopre, ako nekom zatreba neka se javi. [ Bojan Basic @ 25.06.2004. 14:04 ] @
A sada - veliko finale!!!
Naime, moj zaključak do kojeg sam došao glasi:
Za svaki niz, sa datim proizvoljnim brojem početnih članova, se može naći beskonačno mnogo rekurzivnih formula, koje sadrže samo dva člana, a svaka od njih nastavlja niz drugim brojem.
Pre nego što ispišem dokaz ovoga (a prilično je jednostavno), dajte neke primere čisto da proverim hoće li moja ideja proći, pa ukoliko to bude slučaj dobićete celo obrazloženje.
[ srki @ 25.06.2004. 14:14 ] @
213 62 42 43 2 8 35...
Nastavi ovaj niz. Daj mi dve rekurentne formule koje vaze za sve clanove niza (osim za prva dva) i nastavlja niz razlicitim brojevima.
[ Bojan Basic @ 25.06.2004. 15:21 ] @
Stvarno bi hteo? 
OK, izvoli pa proveri:
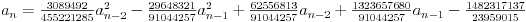
ili
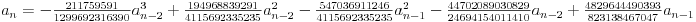
U prvom slučaju sledeći član je 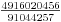 , a u drugom 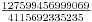 .
Postoji još gomila formula za ovaj primer, nisam siguran da li su sve ovakve ili ima i jednostavnijih, potražiću sad neku jednostavniju pa ako nađem javiću se. [ -zombie- @ 25.06.2004. 19:53 ] @
svaka čast! ;)
jedva čekam dokaz i objašnjenje, i kako si došao do otkrića.. ;)
[ Bojan Basic @ 25.06.2004. 20:23 ] @
Evo, neću da pravim nikakvu nauku od toga, sve je vrlo jednostavno.
Ako imamo zadato prvih n članova treba da sastavimo kako nam god padne na pamet sistem od n-2 jednačine sa n-2 nepoznate (zbog toga što prva su prva dva broja nezavisna, a svi ostali prema hipotezi se mogu dobiti od njih, rekurentno). Tada samo rešimo sistem i dobijemo koeficijente koji figurišu u rekurentnoj formuli, onda odaberemo drugi sistem i dobijemo drugu rekurentnu formulu, itd. Npr., na srkijevom primeru to izgleda ovako:
Lupetanje 1:
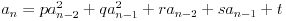
Jedino što treba paziti je da imamo n-2 (u ovom slučaju 5) nepoznate (to su p, q, r, s i t). U ovu jednačinu sam 5 puta uvrstio vrednosti koje je srki dao, i tako dobio sistem od 5 linearnih jednačina sa 5 rešenja, rešavanjem toga se dobije malopre napisana formula.
Lupetanje 2:
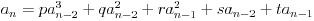
Na isti način dobijem drugačiji sistem koji ima drugačija rešenja, pa je i rekurzivna formula drugačija, i napisana je u mojoj prošloj poruci.
E sad, očigledno je da možemo puštati mašti na volju kako želimo, ali neko se ipak može zapitati postoji li ipak neka granica, a odgovor na to pitanje je ne. Pogledajmo primer "lupetanje 2", i dodajmo na desnu stranu te jednačine proizvoljnu konstantu. Očigledno je da na ovaj način dobijamo sasvim novi sistem, što nam obezbeđuje beskonačnost rešenja. Naravno, ne moramo se ograničavati samo na jednačine ovog tipa, možemo se iživljavati koliko god hoćemo, evo za ilustraciju nešto čime sam se danas igrao:
Nastaviti niz 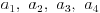 .
Evo, neka je naša rekurentna formula ovakva:
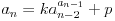
Znači, naš sistem (dve jednačine sa dve nepoznate) izgleda ovako:
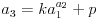
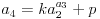
Pretpostavljam da svako zna da reši ovaj sistem po k i p (npr. iz prve jednačine jednostavno izrazimo p i uvrstimo u drugu), i kao rešenja dobijemo sledeću zavisnost:
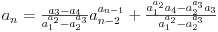
Možemo probati i konkretan primer, npr. niz 1, 2, 3, 4, i dobijemo ovu zavisnost:
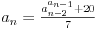
A tek ako ubacimo i trigonometrijske funkcije... Ostavljam vas da se sami igrate koliko želite  [ Nedeljko @ 25.06.2004. 22:23 ] @
Postoje nizovi koje ne mogu opisati rekurentnom formulom u kojoj se svaki element počev od trećeg izražava preko dva prethodna.
Primer:
1,2,3,1,2,4,...
Ako bi ga opisao rekurentnom formulom oblika 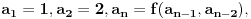 onda bi moralo da bude f(1,2)=3 i f(1,2)=4, a samim tim i 3=4, što je nemoguće.
No, ako ti je dato prvih n članova niza  onda taj niz možeš produžiti na proizvoljan način sa m članova do niza 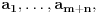 zatim naći Lagranžev interpolacioni polinom p(x) stepena manjeg od m+n za koji će važiti 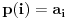 za 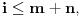 i onda ako je k stepen polinoma p(x) i A njegov vodeći koeficijent napisati rekurentnu formulu
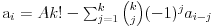 za 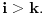
O tome vam i pričam od početka da je svaki konačan niz "pravilan", i da time cela priča gubi svaki smisao. Kako god da konačan niz produžimo sa konačno mnogo članova, možemo naći polinom koji će "proći" kroz te čvorove i upotrebiti ga kao opštu formulu za ceo niz. Znači, prrvih konačno mnogo članova nam ne pruža nikakvu informaciju o sledećim članovima. To je ona proizvoljnost u izboru produženja konačnog niza konačnim brojem članova.
Ovde polinom p(x) ne mora ni da se računa. Gornja formula će sigurno da radi za k=m+n-1 i neko A koje se izračunava zamenjivanjem i sa m+n. No, to nije ni preterano važno.
[ Ovu poruku je menjao Nedeljko dana 26.06.2004. u 01:05 GMT] [ Bojan Basic @ 25.06.2004. 22:45 ] @
Da, ovaj Nedeljkov niz je izuzetak jer tada sistem linearnih jednačina o kojem sam pričao postaje protivrečan, ali ima relativno malo takvih stvari, a i nije neki problem malo korigovati moje rešenje, samo ukoliko je niz ovakav uzmemo 3 rekurzivna člana.
[ Nedeljko @ 25.06.2004. 23:18 ] @
Nije mi baš najjasniji pojam rešenja budući da postavka zadatka nema nikakvog smisla.
[ Bojan Basic @ 25.06.2004. 23:39 ] @
Zašto misliš da nema smisla?
Postavka zadatka koji sam rešavao bi išla nekako ovako:
Dokazati da se za svaki niz sa datim proizvoljnim brojem n početnih članova može pronaći beskonačno mnogo rekurzivnih formula takvih da u rekurzivnoj formuli učestvuje m članova, 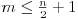 . .
Možda fali neki detalj, ali tako bi otprilike izgledala postavka, ne pišem sad za neku literaturu pa da bih sve morao precizno da sročim. Moje rešenje se svodi da dokažem da je u većini slučajeva (nazovimo to "opšti slučaj") dovoljno m=2, a posle tvoje poruke sam samo korigovao, ukoliko niz koji si dao i slične smatramo "specijalnim slučajevima" kako onda možemo menjanjem m da postignemo cilj [ Nedeljko @ 26.06.2004. 01:22 ] @
Ma, mislio sam na zadatak o kome sve vreme diskutujemo: "Produžiti niz ako je dato prvih nekoliko članova". Apsolutno nema nikakvog smisla.
[ chupcko @ 26.06.2004. 15:43 ] @
Uf, koliko ja shvatam Nedeljka, on zeli da pokaze da je postavka zadatka besmislena, jer postoji puno razlicitih resenja, cak verujem da ih ima prebrojivo mnogo ...
Ono sto bi trebalo da trazi (a obicno se trazi) da resenje bude jednostavnog oblika, e sada to jednostavnog oblika je tesko tacno formalno definisati.
Recimo jedna od definicija bi bila tipa:
Prebacimo formulu u prefiksni oblik (operatore i konstatne pisemo kao funkcije).
Za svaku promenjljivu ili spominjanje elemnta (rekuretnog) niza dodajte 1 poen.
Za svaku pojavu funkcija +, -, *, /, ^ dodajte 2 peona.
Za pojavu svih ostalig funkcija dodajte 5 poena.
...
Dakle svaka funkcija ima jedinstveno odredjenu vrednost poena.
Ima tu jos raznih osobina.
E sada mozete traziti funkciju koja opisuje niz, a da od svih ostalih funkcija koje isto opisuju taj niz ima najmanje poena :).
Uzgred, ja sam uvek kada mi neko kaze: nastavi niz 32, 45, 23, 124, 98, ... odgovarao : 3
[ salepronalazac @ 28.06.2004. 18:04 ] @
resenje postavljenog zadatka je
12
27 2.25
167 6.185185185 2.748971193
4015 24.04191617 3.887016386 1.413989494
530622.9105 132.1601271 5.497071291 1.414213562 -0.000224069
530622.9105
tj 530623
[ chupcko @ 29.06.2004. 07:54 ] @
Mislis jedno od resenja :)
[ Nedeljko @ 29.06.2004. 11:30 ] @
To rešenje je rešenje koliko i bilo koji konačan niz koji proužava dati niz.
[ salepronalazac @ 29.06.2004. 16:12 ] @
Slazem se sa svima vama koji ste izneli odredjena pravila za postavljanje niza. Jedno od njih je da odredjeno pravilo mora da se ponovi bar dva puta. Medjutim ovo je resenje koje je hteo da cuje onaj koji ce mi platiti pivo, vrlo je jednostavno.
Ukljucite Excel. Poredjajte date brojeve pa svaki veci podelite sa predhodnim manjim. Ostaju vam tri broja. Uradite to opet... itd, dok vam ne ostane samo jedan... 1.41.... mnogo je za slucajnost. Rezultat koji sam ja dao zavrsava se sa .2,9.. ta greska je nastala jer sam zaokruzivao na dve deciomale. Tako da je resenje 530623. Vrlo je jednostavno, nazovimo to geometrijskom progresijom treceg stepena/nivoa/ili kako god vec, jer nisam bas potkovan matematickom teorijom-nazalost!
[ Prgavi @ 08.08.2015. 16:58 ] @
481809
Copyright (C) 2001-2024 by www.elitesecurity.org. All rights reserved.
|