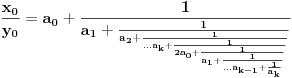
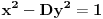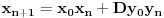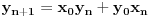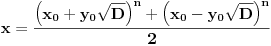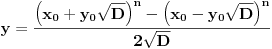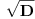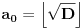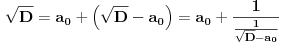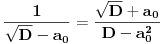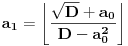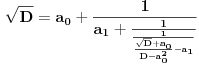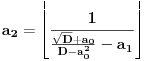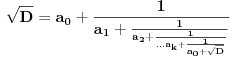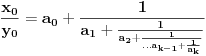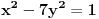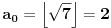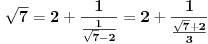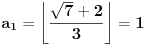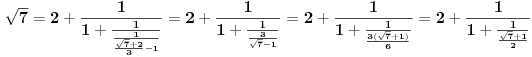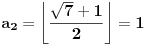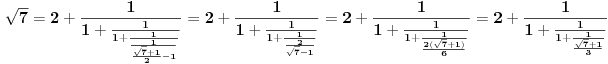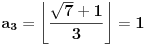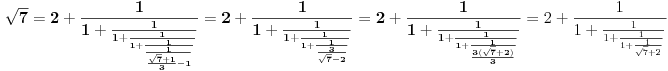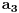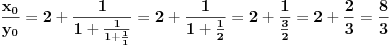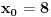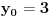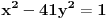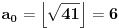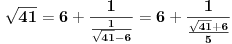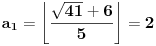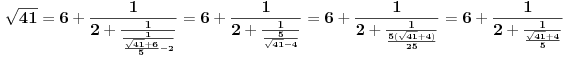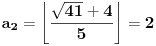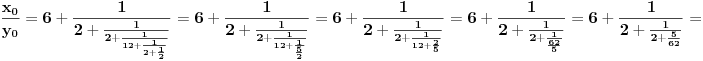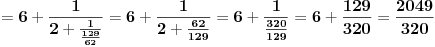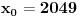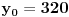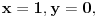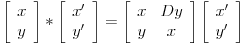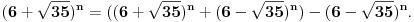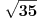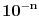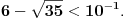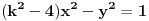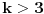[ Bojan Basic @ 09.03.2005. 16:21 ] @
|
[ filmil @ 09.03.2005. 19:08 ] @
Citat: continued fraction verižni razlomak f [ Bojan Basic @ 10.03.2005. 22:01 ] @
Da vidimo šta se dešava kada je na desnoj strani jednačine broj različit od
 . Podelićemo teoriju na dva dela. . Podelićemo teoriju na dva dela.Jednačine oblika 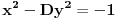 : :Veza između rešenja jednačine ovog oblika: Za jednačinu oblika 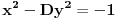 vezuje se sledeće svojstvo: ukoliko ima jedno rešenje onda ih ima beskonačno mnogo, medjutim postoji mogućnost i da jednačina nema rešenja. Važi ista formula kao i za Pelovu jednačinu, to jest da ukoliko je par vezuje se sledeće svojstvo: ukoliko ima jedno rešenje onda ih ima beskonačno mnogo, medjutim postoji mogućnost i da jednačina nema rešenja. Važi ista formula kao i za Pelovu jednačinu, to jest da ukoliko je par 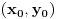 rešenje date jednačine onda su to i parovi rešenje date jednačine onda su to i parovi 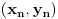 takvi da je takvi da je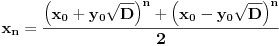 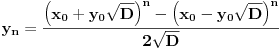 uz napomenu da u ovom slučaju  može da uzima samo neparne vrednosti. može da uzima samo neparne vrednosti.Opšti postupak rešavanja: Opšti postupak rešavanja jednačine ovog oblika ne razlikuje se mnogo od postupka opisanog u prethodnoj poruci. Razlika je samo u sledećem — u momentu kada stanemo važi: ako je indeks poslednjeg izračunatog elementa neparan, jednačina nema nijedno rešenje, u suprotnom minimalno rešenje je par uzajamno prostih brojeva  takav da je takav da je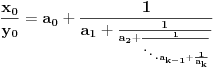 Jednačine oblika 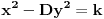 : :I za jednačinu ovog oblika važi da ukoliko ima jedno rešenje onda ih ima beskonačno mnogo. Vrlo bitna stvar je da ovakva jednačina (za 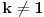 ) ima rešenja ako jednačina za ) ima rešenja ako jednačina za 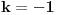 ima rešenja. Opšti postupak za rešavanje jednačina ovog tipa nije poznat, ali je poznata sledeća činjenica: ako je ima rešenja. Opšti postupak za rešavanje jednačina ovog tipa nije poznat, ali je poznata sledeća činjenica: ako je 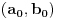 jedno rešenje date jednačine, i ako su su jedno rešenje date jednačine, i ako su su 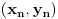 rešenja jednačine za rešenja jednačine za 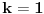 , onda su rešenja date jednačine parovi , onda su rešenja date jednačine parovi 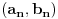 takvi da je takvi da je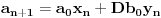 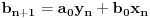 [Ovu poruku je menjao Bojan Basic dana 15.01.2007. u 15:28 GMT+1] [ Bojan Basic @ 16.03.2005. 02:08 ] @
Da vidimo sad kako izgleda primena Pelove jednačine u praksi. Evo nekoliko zadataka, pa ko ima volje neka pokuša da ih reši, ako ne bude interesovanja objaviću rešenja naknadno:
1) Dokazati da su prvih 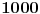 cifara iza decimalnog zareza broja cifara iza decimalnog zareza broja 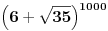 jednake jednake 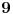 . .2) Naći prirodan broj 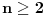 takav da je kvadratna sredina prvih takav da je kvadratna sredina prvih  prirodnih brojeva prirodan broj. prirodnih brojeva prirodan broj.3) Postoji li prirodan broj  takav da jednačina takav da jednačina 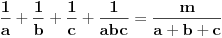 ima beskonačno mnogo rešenja u skupu prirodnih brojeva? ima beskonačno mnogo rešenja u skupu prirodnih brojeva?4) Posmatrajmo sistem jednačina: 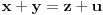 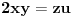 Pronaći maksimalnu vrednost realnog broja  takvog da je takvog da je 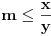 za sva rešenja gornjeg sistema iz skupa prirodnih brojeva za koje važi za sva rešenja gornjeg sistema iz skupa prirodnih brojeva za koje važi 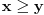 . .Zadaci su sortirani po težini (po mojoj proceni). Prvi je zaista trivijalan i može da se reši na mnogo načina, ovde stoji samo kao ilustracija. Drugi je isto lak, ali znatno teže ide elementarno nego primenom Pelove jednačine. Treći je dosta teži, elementarno rešenje koje ja znam je prilično komplikovano ali primenom Pelove jednačine ga možemo rešiti na znatno kraći način. Četvrti je definitivno najteži, ima nekoliko različitih rešenja (ja znam tri) od kojih su sva manje-više iste dužine i složenosti a jedno od njih na lep način ilustruje primenu Pelove jednačine. [ Nedeljko @ 17.06.2005. 10:09 ] @
[ Nedeljko @ 17.06.2005. 13:55 ] @
[ Nedeljko @ 13.01.2007. 00:41 ] @
Citat: Bojan Basic: Evo nekoliko zadataka, pa ko ima volje neka pokuša da ih reši, ako ne bude interesovanja objaviću rešenja naknadno: Evo, za par meseci će proći dve godine kako Bojan Bašić nije postovao nijedno od najavljenih rešenja. Neka je  bilo koji prirodan broj. Primenom binomne formule zaključujemo da za neke prirodne brojeve bilo koji prirodan broj. Primenom binomne formule zaključujemo da za neke prirodne brojeve 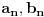 važi važi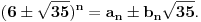 Konkretno, 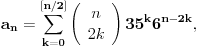 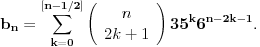 Tu je 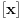 oznaka za najveći ceo broj koji nije veći od oznaka za najveći ceo broj koji nije veći od 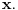 Iz Iz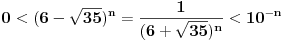 zaključujemo da je 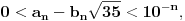 odnosno 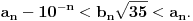 Odatle i iz 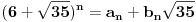 zaključujemo da je zaključujemo da je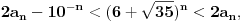 što tačno znači da iza decimalnog zareza, u zapisu broja 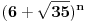 imamo najmanje imamo najmanje  devetki. devetki.[ Nedeljko @ 13.01.2007. 01:21 ] @
Neka je
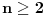 takav prirodan broj da je takav prirodan broj da je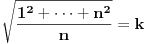 za neki prirodan broj 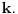 Znajući da je Znajući da je 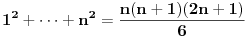 (što se dokazuje matematičkom indukcijom) zaključujemo da je (što se dokazuje matematičkom indukcijom) zaključujemo da je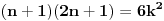 Pošto je na desnoj strani paran broj, a broj 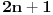 je svakako neparan, broj je svakako neparan, broj  mora biti paran, odnosno, broj mora biti paran, odnosno, broj  je neparan, pa postoji ceo broj je neparan, pa postoji ceo broj  takav da je takav da je 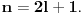 Iz uslova da je Iz uslova da je 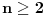 zaključujemo da je zaključujemo da je 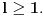 Na osnovu prethodne jednačine je Na osnovu prethodne jednačine je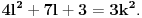 Svođenjem leve strane na potpun kvadrat i množenjem sa 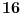 dobija se dobija se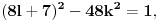 što smenom 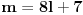 postaje Pelova jednačina postaje Pelova jednačina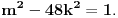 Najmanje rešenje te jednačine je 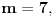 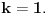 Međutim, nas zanima najmanje rešenje te jednačine kod koga je Međutim, nas zanima najmanje rešenje te jednačine kod koga je 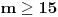 i i 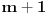 deljivo sa deljivo sa 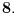 Prethodno opisanim postupkom nalazi se da je Prethodno opisanim postupkom nalazi se da je  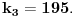 Odatle se lako izvodi da je Odatle se lako izvodi da je 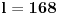 i najzad i najzad 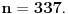 [ Nedeljko @ 13.01.2007. 13:38 ] @
Neka su
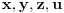 prirodni brojevi za koje je prirodni brojevi za koje je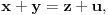 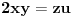 i takvi da je 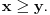 U tom slučaju je U tom slučaju je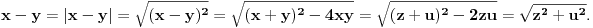 Odavde sledi da je zapravo 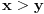 (jer je (jer je 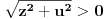 ) i da brojevi ) i da brojevi 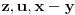 obrazuju tzv. Pitagorinu trojku. Drugim rečima, obrazuju tzv. Pitagorinu trojku. Drugim rečima,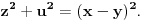 Identitet 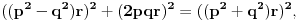 gde su 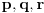 prirodni brojevi za koje je prirodni brojevi za koje je 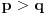 , kao što je poznato, predstavlja opšti oblik Pitagorinih trojki do na redosled sabiraka sa leve strane jednakosti. Pošto su uslovi po , kao što je poznato, predstavlja opšti oblik Pitagorinih trojki do na redosled sabiraka sa leve strane jednakosti. Pošto su uslovi po 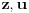 simetrični, možemo pretpostaviti da za neke prirodne brojeve simetrični, možemo pretpostaviti da za neke prirodne brojeve 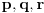 za koje je za koje je 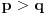 važi važi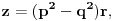 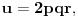 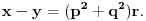 Iz 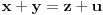 zaključujemo da je zaključujemo da je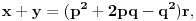 a samim tim i 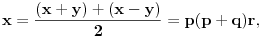 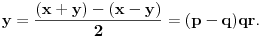 Stoga je 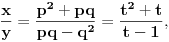 za 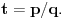 Iz Iz  zaključujemo da je zaključujemo da je  racionalan broj veći od racionalan broj veći od 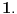 Na intervalu Na intervalu 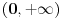 funkcija funkcija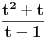 dostiže minimum u tački dostiže minimum u tački 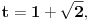 gde ima vrednost gde ima vrednost 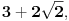 što je najveći realan broj što je najveći realan broj  za koji pod navedenim uslovima uvek važi za koji pod navedenim uslovima uvek važi 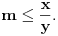 [ Bojan Basic @ 13.01.2007. 14:21 ] @
Citat: Nedeljko: Evo, za par meseci će proći dve godine kako Bojan Bašić nije postovao nijedno od najavljenih rešenja. Nije bilo velikog interesovanja za temu pa se nisam ni ja nametao kako bi neko ko eventualno na nju kasnije nabasa imao priliku da sam reši zadatke. Naravno, ako neko zatraži rešenja vrlo radu ću ih napisati, kao što sam i pomenuo u temi o nerešenim zadacima (gde su i ovi uvršteni). Tvoja rešenja su u redu, s tim što u prvom i četvrtom nisi koristio Pelovu jednačinu, pa ću napisati i kako se ona može primeniti u ovim zadacima. 1) Zapažamo da je minimalno rešenje Pelove jednačine 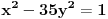 par par 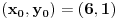 iz čega sledi da su ostale vrednosti nepoznate iz čega sledi da su ostale vrednosti nepoznate  opisane formulom opisane formulom 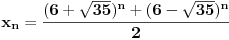 , pa zaključujemo da je , pa zaključujemo da je 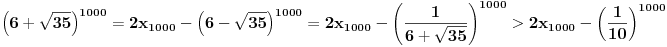 . .Pošto je 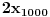 ceo broj iz ceo broj iz 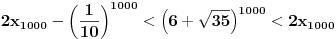 sledi tvrđenje zadatka. sledi tvrđenje zadatka.4) Rešenje je prilično blisko Nedeljkovom, ali ipak ću ga napisati, kao što sam rekao. Kvadriramo prvu jednačinu i četiri puta oduzmemo drugu. Dobijamo: 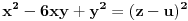 iz čega sledi 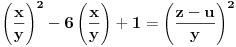 Kvadratna funkcija 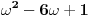 ima nule u tačkama ima nule u tačkama 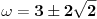 i za i za 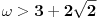 je pozitivna. Pošto je desna strana dobijene jednačine uvek pozitivna (jer je potpun kvadrat) sledi da i leva strana mora biti pozitivna, pa kako je je pozitivna. Pošto je desna strana dobijene jednačine uvek pozitivna (jer je potpun kvadrat) sledi da i leva strana mora biti pozitivna, pa kako je 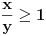 imamo imamo 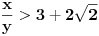 . Potrebno je još dokazati da vrednost izraza . Potrebno je još dokazati da vrednost izraza 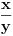 može biti proizvoljno blizu broju može biti proizvoljno blizu broju 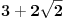 , što bi značilo da je , što bi značilo da je 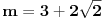 . Ovo ćemo dokazati na taj način što ćemo pokazati da vrednost izraza . Ovo ćemo dokazati na taj način što ćemo pokazati da vrednost izraza 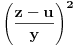 može biti proizvoljno mala. može biti proizvoljno mala.Ako postoji prost broj  takav da takav da 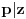 i i 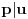 , onda iz datih relacija dobijamo da , onda iz datih relacija dobijamo da 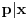 i i 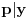 pa bez umanjenja opštosti možemo pretpostaviti da su pa bez umanjenja opštosti možemo pretpostaviti da su  i i  uzajamno prosti brojevi. Ako kvadriramo prvu jednačinu pa dva puta oduzmemo drugu dobijamo uzajamno prosti brojevi. Ako kvadriramo prvu jednačinu pa dva puta oduzmemo drugu dobijamo 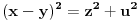 , iz čega na osnovu poznate osobine Pitagorinih trojki uz pretpostavku da je , iz čega na osnovu poznate osobine Pitagorinih trojki uz pretpostavku da je  paran broj sledi da postoje prirodni paran broj sledi da postoje prirodni  i i  takvi da je takvi da je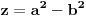 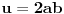 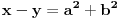 Uvrštajući ovo u jednačinu 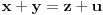 , dobijamo , dobijamo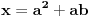 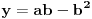 Primetimo da je 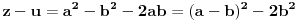 . Uzimajući da je . Uzimajući da je 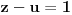 dobijamo Pelovu jednačinu dobijamo Pelovu jednačinu  . Znamo da ova jednačina ima beskonačno mnogo rešenja za . Znamo da ova jednačina ima beskonačno mnogo rešenja za 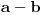 i i  , i obe ove vrednosti mogu biti proizvoljno velike. Sledi da i , i obe ove vrednosti mogu biti proizvoljno velike. Sledi da i 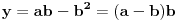 može biti proizvoljno veliko, što znači da vrednost izraza može biti proizvoljno veliko, što znači da vrednost izraza 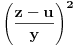 tj. tj. 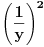 može biti proizvoljno mala, čime je zadatak rešen. može biti proizvoljno mala, čime je zadatak rešen.Pomenuo sam da znam ukupno tri rešenja ovog zadatka. Ovo je jedino koje se bazira na Pelovoj jednačini, ali ako nekog zanima i to što je ostalo, rado ću napisati. Ostao je još treći zadatak. Nedeljko, nisam te baš najbolje razumeo kad si me pozvao da se uključim u temu, želiš li da objavim rešenje ili ćeš pokušati još malo? [ Nedeljko @ 13.01.2007. 14:58 ] @
Mislio sam da se dokumentuju rešenja svih zadataka. Ja sam dao rešenja za tri, pa sam mislio da ostavim i tebi nešto. No, u prvom i četvrtom namerno nisam koristio Pelovu jednačinu, jer smatram da joj nije mesto tamo gde ne pojednostavljuje rešenje. Za četvrti zadatak se ne bih složio da su nam rešenja slična, ali smatram da su nam rešenja prvog zadatka gotovo identična. Ja sam razvio stepene binoma u sume i to je to. Šta će mi Pelova jednačina da bih zaključio da je
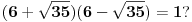 Ako isti dokaz prolazi bez skraćivenja i bez osobina Pelove jednačine, onda Pelovoj jednačini tu jednostavno nije mesto. Ako isti dokaz prolazi bez skraćivenja i bez osobina Pelove jednačine, onda Pelovoj jednačini tu jednostavno nije mesto.[ Nedeljko @ 13.01.2007. 19:34 ] @
[ Bojan Basic @ 14.01.2007. 16:23 ] @
Pitanje je otkud znamo da je izraz u zagradi ceo broj. Ti kažeš kako iz binomne formule sledi da se neparni stepeni potiru; dobro, to je jedan način. Ja sam hteo da pokažem kako se do istog zaključka može doći i zahvaljujući Pelovoj jednačini; to ne znači da je ovo najjednostavniji način, ali ovde stoji samo kao ilustracija da se i tu može primeniti Pelova jednačina. Zašto ti to toliko smeta?
Evo i preostala dva rešenja četvrtog zadatka, ako nekog zanimaju. Lično smatram da su veoma inventivna. 4) Geometrijsko rešenje: Kao i dosad, zaključujemo da je 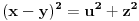 . Dakle, postoji pravougli trougao . Dakle, postoji pravougli trougao 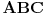 sa katetama sa katetama 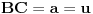 i i 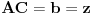 i hipotenuzom i hipotenuzom 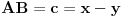 . Neka je . Neka je  centar upisane kružnice a centar upisane kružnice a  njen poluprečnik, i neka je njen poluprečnik, i neka je 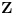 tačka dodira upisane kružnice i hipotenuze. Neka je tačka dodira upisane kružnice i hipotenuze. Neka je 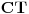 ( (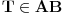 ) simetrala ugla ) simetrala ugla  , neka je , neka je 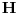 podnožje normale iz podnožje normale iz  na na  , i neka je , i neka je 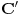 sredina stranice sredina stranice  . .Kako je trougao pravougli, važi 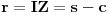 (gde je (gde je  poluobim). Dakle, poluobim). Dakle, 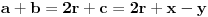 . Iz ovoga i . Iz ovoga i 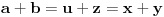 dobijamo dobijamo 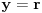 i i 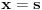 . Sada ćemo dokazati da za ma koje vrednosti . Sada ćemo dokazati da za ma koje vrednosti  i i  važi važi 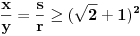 . .Da bismo ovo dokazali, primetimo da je 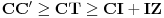 , dakle , dakle 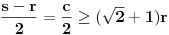 . Sledi da je . Sledi da je 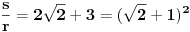 , čime je željena nejednakost dokazana. , čime je željena nejednakost dokazana.Jednakost važi samo ako je trougao jednakostraničan, ali u tom slučaju stranice mu ne mogu biti prirodni brojevi; prema tome, nejednakost je stroga. S druge strane, 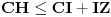 pa je pa je 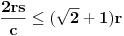 . Prema tome, važi . Prema tome, važi 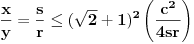 . Međutim, . Međutim, 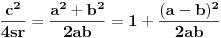 . Pošto postoji beskonačno mnogo pitagorejskih trojki . Pošto postoji beskonačno mnogo pitagorejskih trojki 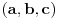 za koje važi za koje važi  , sledi da , sledi da 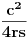 može biti proizvoljno blizu jedinici. Sada je jasno da je tražena vrednost može biti proizvoljno blizu jedinici. Sada je jasno da je tražena vrednost  jednaka jednaka 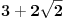 . .Rešenje preko analitičke geometrije: Rešimo prvu jednačinu po  , zamenimo u drugu, i podelimo sve sa , zamenimo u drugu, i podelimo sve sa 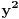 da bismo dobili da bismo dobili 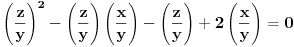 . Neka je . Neka je 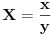 i i 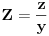 , pa se gornja relacija svodi na , pa se gornja relacija svodi na 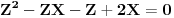 . Ovo je jednačina hiperbole u . Ovo je jednačina hiperbole u 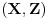 -ravni. Koeficijenti pravaca asimptota su -ravni. Koeficijenti pravaca asimptota su  i i  . Jedna grana hiperbole leži u poluravni . Jedna grana hiperbole leži u poluravni 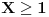 , druga u poluravni , druga u poluravni  . Štaviše, „najlevlja“ tačka grane u poluravni . Štaviše, „najlevlja“ tačka grane u poluravni 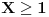 ima koordinate ima koordinate 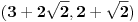 . Dakle, ako je . Dakle, ako je 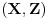 na hiperboli i na hiperboli i 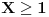 , onda je , onda je 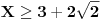 , i ova ocena je najbolja moguća. Pošto su koeficijenti u jednačini hiperbole racionalni brojevi i hiperbola ima tačku s racionalnim koordinatama, sledi da ima beskonačno mnogo tačaka s racionalnim koordinatama. Neka je , i ova ocena je najbolja moguća. Pošto su koeficijenti u jednačini hiperbole racionalni brojevi i hiperbola ima tačku s racionalnim koordinatama, sledi da ima beskonačno mnogo tačaka s racionalnim koordinatama. Neka je  racionalan broj različit od racionalan broj različit od  i i  . Tada prava . Tada prava 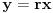 seče hiperbolu u tačkama seče hiperbolu u tačkama 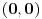 i i 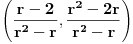 . Ako je . Ako je 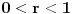 , onda se druga po redu tačka preseka nalazi na desnoj grani hiperbole, pa ima (racionalnu) , onda se druga po redu tačka preseka nalazi na desnoj grani hiperbole, pa ima (racionalnu)  koordinatu koordinatu 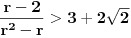 . Štaviše, ako je . Štaviše, ako je  blisko blisko 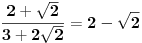 , onda je ova , onda je ova  -koordinata blizu -koordinata blizu 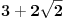 . Konačno, ako su . Konačno, ako su  i i 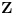 pozitivni racionalni brojevi koji zadovoljavaju jednačinu hiperbole, uvek možemo naći cele brojeve takve da je pozitivni racionalni brojevi koji zadovoljavaju jednačinu hiperbole, uvek možemo naći cele brojeve takve da je 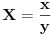 i i 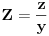 . Lako je proveriti da su ovako odabrani . Lako je proveriti da su ovako odabrani 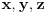 i i 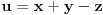 prirodni brojevi koji zadovoljavaju jednačine iz postavke zadatka, i kad je prirodni brojevi koji zadovoljavaju jednačine iz postavke zadatka, i kad je 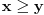 važi važi 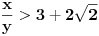 , pri čemu je ova granica najbolja moguća. , pri čemu je ova granica najbolja moguća.Trenutno sam u žurbi, pa rešenje trećeg zadatka ostavljam za nešto kasnije. [ Bojan Basic @ 15.01.2007. 15:24 ] @
Evo rešenja i trećeg zadatka (ovo će biti po Nedeljkovom ukusu, budući da Pelova jednačina znatno pojednostavljuje rešenje).
3) Rešenje bez Pelove jednačine: Za 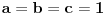 utvrđujemo da je utvrđujemo da je  . Dokazaćemo da baš za . Dokazaćemo da baš za  postavljena jednačina ima beskonačno mnogo rešenja u skupu prirodnih brojeva. Neka je, radi lakšeg zapisa, postavljena jednačina ima beskonačno mnogo rešenja u skupu prirodnih brojeva. Neka je, radi lakšeg zapisa, 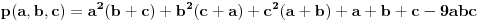 (to je izraz koji se dobije kada prebacimo sve na levu stranu jednačine i svedemo na zajednički imenilac). Potrebno je dokazati da za beskonačno mnogo vrednosti (to je izraz koji se dobije kada prebacimo sve na levu stranu jednačine i svedemo na zajednički imenilac). Potrebno je dokazati da za beskonačno mnogo vrednosti  , ,  i i  izraz izraz 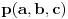 uzima vrednost uzima vrednost  . Neka je . Neka je 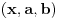 rešenje za koje važi rešenje za koje važi 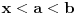 . Posmatrajući izraz . Posmatrajući izraz 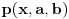 kao kvadratnu jednačinu po kao kvadratnu jednačinu po  , vidimo da je , vidimo da je 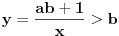 takođe rešenje, ali je potrebno ustanoviti da je takođe rešenje, ali je potrebno ustanoviti da je  prirodan broj. prirodan broj.Neka je 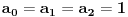 , i definišimo , i definišimo 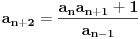 za sve za sve 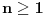 . Indukcijom ćemo istovremeno dokazati sledeća tvrđenja: . Indukcijom ćemo istovremeno dokazati sledeća tvrđenja:(i) 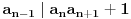 (ii) 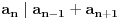 (iii) 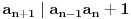 Sva tri tvrđenja važe za  , pa pretpostavimo da važe za , pa pretpostavimo da važe za 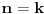 . .Iz (i) sledi da su 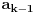 i i 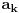 uzajamno prosti i da uzajamno prosti i da 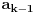 deli deli 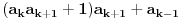 , dok nam (ii) daje , dok nam (ii) daje 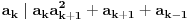 , pa imamo , pa imamo 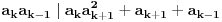 , iz čega sledi , iz čega sledi 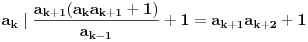 , što je (i) za , što je (i) za 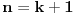 . . Slično, (i) takođe implicira da su 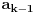 i i 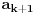 uzajamno prosti, i da je uzajamno prosti, i da je 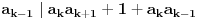 , dok nam (iii) daje , dok nam (iii) daje 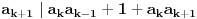 , pa imamo , pa imamo 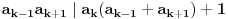 , iz čega sledi , iz čega sledi 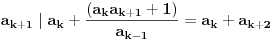 , što je (ii) za , što je (ii) za 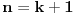 . .Konačno, definicija 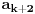 zajedno sa (i) implicira zajedno sa (i) implicira 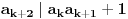 , što je (iii) za , što je (iii) za 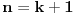 . .Da zaključimo, 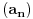 je niz prirodnih brojeva, strogo rastućih za je niz prirodnih brojeva, strogo rastućih za 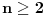 , i , i 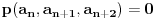 za sve za sve  . Drugim rečima, . Drugim rečima, 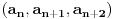 jeste rešenje date jednačine, pri čemu je jeste rešenje date jednačine, pri čemu je Rešenje pomoću Pelove jednačine: Za 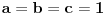 utvrđujemo da je utvrđujemo da je 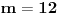 . Dokazaćemo da baš za . Dokazaćemo da baš za  postavljena jednačina ima beskonačno mnogo rešenja u skupu prirodnih brojeva. Neka je, radi lakšeg zapisa, postavljena jednačina ima beskonačno mnogo rešenja u skupu prirodnih brojeva. Neka je, radi lakšeg zapisa,  (to je izraz koji se dobije kada prebacimo sve na levu stranu jednačine i svedemo na zajednički imenilac). Potrebno je dokazati da za beskonačno mnogo vrednosti (to je izraz koji se dobije kada prebacimo sve na levu stranu jednačine i svedemo na zajednički imenilac). Potrebno je dokazati da za beskonačno mnogo vrednosti  , ,  i i  izraz izraz  uzima vrednost uzima vrednost  . Primetimo da je . Primetimo da je Izraz u zagradi je ništa drugo nego Pelova jednačina 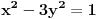 a samim tim ima beskonačno mnogo rešenja, i time je zadatak rešen. a samim tim ima beskonačno mnogo rešenja, i time je zadatak rešen.Napomene: 1. U prvom rešenju niz 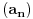 svakako nije jedini niz koji smo mogli iskoristiti u dokazu. Još jedan način je, primera radi, da definišemo niz svakako nije jedini niz koji smo mogli iskoristiti u dokazu. Još jedan način je, primera radi, da definišemo niz 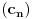 kao kao 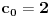 , , 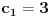 , , 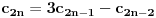 i i 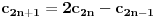 , pa da indukcijom pokažemo da je svaka trojka , pa da indukcijom pokažemo da je svaka trojka 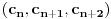 rešenje date jednačine. rešenje date jednačine.2. Ni po čemu 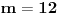 nije posebno. Zapravo, uz malo više teorije o kvadratnim formama može se pokazati da ukoilko jednačina za dato nije posebno. Zapravo, uz malo više teorije o kvadratnim formama može se pokazati da ukoilko jednačina za dato  ima bar jedno rešenje u skupu prirodnih brojeva, onda ih ima beskonačno mnogo; a lako je dokazati da postoji beskonačno mnogo vrednosti ima bar jedno rešenje u skupu prirodnih brojeva, onda ih ima beskonačno mnogo; a lako je dokazati da postoji beskonačno mnogo vrednosti  za koje jednačina ima bar jedno rešenje u skupu prirodnih brojeva. za koje jednačina ima bar jedno rešenje u skupu prirodnih brojeva.[ Bojan Basic @ 15.01.2007. 15:28 ] @
[ trifunca @ 31.03.2007. 00:42 ] @
ako uzmemo da je k vece od 3,onda jednacina moze ovako da izgleda
(4^2-4)x^2-y^2=1 16x^2-y^2=1 16x^2=1+y^2 posto na desnoj strani imamo 1+ kvadrat bilo kog broja,to ne moze biti ceo broj,jer ne postoji kvadrat koji moze zadovoljiti levu stranu,ako je k 4,5,6... [ petarm @ 30.03.2008. 09:04 ] @
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|