Ja sam pokušavao elementarno ali nikako nisam tako uspeo da je rešim. Rešenje metodom "teške artiljerije" bi išlo otprilike ovako:

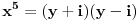
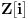
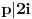
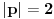
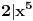
Imamo da je . Pretpostavimo da činioci na desnoj strani imaju zajednički prost faktor u domenu . To bi značilo da taj faktor deli i njihovu razliku, tj. , iz čega zaključujemo da je , a to bi značilo da , odnosno da je paran broj. Dakle, u tom slučaju bi leva strana bila deljiva sa , dok primenom jednostavne kongruencije imamo da desna strana pri takvom deljenju može davati ostatke , , ili , što je kontradikcija. 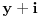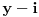Sledi da su i uzajamno prosti u domenu . 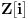Međutim, to dalje znači da je svaki od njih jednak petom stepenu nekog broja, odnosno:

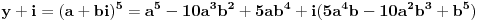
Razmatranjem realnog i imaginarnog dela imamo:


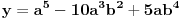
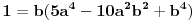
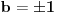
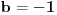
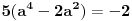
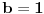
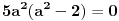
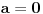
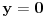
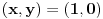
Iz druge relacije sledi . Ako je uvrštavanjem toga u drugu relaciju dobijamo a to je očigledno nemoguće. Preostaje nam mogućnost i ubacivanjem ovoga u drugu relaciju imamo , iz čega neposredno sledi , pa smenom u prvoj relaciji imamo što znači da je jedino rešenje početne jednačine . Eto, prosto i jednostavno :)

Naći celobrojna rešenja jednačine

Evo ja sam malo cackao, i uspio sam dobiti jedno rjesenje, ali nisam siguran da je to i jedino.
Data jednacina se moze napisati u sljecem oblik:


Desna strana jednacine, treba da je pozitivan broj, pa imamo sljedece sisteme jednacina
1.
2.
3.
4.
Rjesavanjem sistema 1. imamo:

Rjesavanjem sistema 2. imamo:
, odakle se vidi da druga jednacina nema cjelobrojnih rjesenja.
Rjesavanjem sistema 3. imamo:
, odakle se vidi da y ne moze biti realno.
Rjesavanje sistema 4.
Iz prve jednacine imamo da je

druga jednacina postaje

posto je i to je pozitivan broj, licno je i , i to je pozitivan broj, pa prema tome, ta jednacina nema rjesenja u skupu cijelih brojeva.
Valjda nisam pogrijesio u rezonu. Pozz

Nije mi baš jasno zašto si raspodelio činioce onako kako si ih raspodelio i nikako drugačije. Teoretski, ako je (tj. bilo kakav složen broj), ništa nas ne sprečava da stavimo npr. , što otvara mnoštvo dodatnih mogućnosti koje treba obraditi.