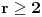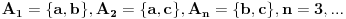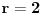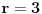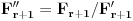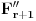[ Bojan Basic @ 14.03.2005. 20:14 ] @
|
[ noviKorisnik @ 14.03.2005. 20:54 ] @
Sad ćeš me još i Tolstojem zvati: šta mu uopšte dođe termin "veličina skupa"?
[ Bojan Basic @ 14.03.2005. 21:11 ] @
Kardinalni broj, odnosno broj elemenata.
[ gpreda @ 15.03.2005. 13:26 ] @
[ Bojan Basic @ 15.03.2005. 13:33 ] @
[ zi:: @ 15.03.2005. 13:41 ] @
[ Bojan Basic @ 15.03.2005. 14:07 ] @
[ noviKorisnik @ 15.03.2005. 19:52 ] @
Ratimir, 2 deo...
Ako je r = 2, to po postavci zadatka govori da imamo familiju (to je porodica, je li, ah...) dvočlanih skupova. Kako su svi oni međusobno različiti a imaju neprazan presek, to mu dođe da su preseci parova skupova jednočlani skupovi... I kad odatle pogledam cilj, ispada da se dokazuje da su svi ovi preseci jednaki (za r = 2)... Što obrtanjem teze dovodi do dokazivanja da je svaka familija dvočlanih nedisjunktnih skupova ima skupove s jednim fiksiranim elementom i drugim slobodnim... Za r > 2 ide indukcija, to je intuicija. [ noviKorisnik @ 15.03.2005. 20:03 ] @
r = 2
jedan skup iz familije je {e0, e1} drugi skup iz familije je {e0, e2} treći skup ne može da bude {e1, e2} jer bi svi ostali bili disjunktni s makar jednim od ova tri - tako je treći skup {e0, e3} i tako u beskonačnost... svi skupovi sadrže {e0} [ Bojan Basic @ 15.03.2005. 20:15 ] @
Slažem se, ali ne vidim kako bi iz ovoga izveo ostale slučajeve (za skupove sa većim brojem elemenata).
[ noviKorisnik @ 15.03.2005. 20:56 ] @
Znaš, ne vidim ni ja, ali gledam i dalje
[ Bojan Basic @ 15.03.2005. 21:35 ] @
Mislim da ipak nije baš toliko jednostavno kao što si krenuo, jeste da se rešava iz dva poteza ali treba se setiti.
[ noviKorisnik @ 15.03.2005. 21:37 ] @
Da li sam spomenuo indukciju?
Naravno, važi za r, pa da vidimo zašto odatle sledi da važi i za r + 1... Jedan skup iz familije je {e0, e1, ..., er}. Od elemenata skupa bar jedan pripada beskonačnom broju preseka skupa s ostalim skupovima familije. Uočimo jedan takav element i sve skupove koji ga imaju. To je podfamilija... Sada napravimo od nje novu familiju koju čine podskupovi tih skupova kojima fali samo ovaj naš veseli zajednički element. Ovi imaju po r elemenata i po pretpostavci postoji skup veličine r - 1 koji ima neprazan presek s baš svakim od njih... A nijedan od njih nema onaj naš veseli pa ga ne bi trebalo ni taj izabrani (ajd ovo neću da dokazujem da se ne upetljavam)... Ali zato imaju ovi naši iz velike familije. Pa kad onom skupu veličine r - 1 dodamo još taj jedan element dobija se skup veličine r u familiji skupova veličine r + 1, itd sve po uslovima zadatka. [ Bojan Basic @ 15.03.2005. 22:10 ] @
Čini mi se da si blizu rešenja, ali mislim da si još uvek pomalo upetljan. Da probam ja to tvoje rešenje da prevedem na matematički jezik pa mi ti reci da li sam dobro razumeo šta hoćeš da kažeš.
Neka je 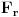 beskonačna familija skupova od po beskonačna familija skupova od po  elemenata koji zadovoljavaju uslove zadatka. Pretpostavimo (indukcijska hipoteza) da za svaku takvu familiju važi tvrđenje. Sada posmatramo familiju elemenata koji zadovoljavaju uslove zadatka. Pretpostavimo (indukcijska hipoteza) da za svaku takvu familiju važi tvrđenje. Sada posmatramo familiju 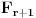 i neka jedan skup iz te familije sadrži elemente i neka jedan skup iz te familije sadrži elemente 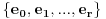 . Očigledno je bar jedan od tih elemenata sadržan u beskonačno mnogo skupova iz familije . Očigledno je bar jedan od tih elemenata sadržan u beskonačno mnogo skupova iz familije 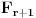 . Neka je to, bez umanjenja opštosti, elemenat . Neka je to, bez umanjenja opštosti, elemenat 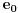 . Sada posmatramo familiju . Sada posmatramo familiju 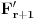 koja se sastoji od skupova iz familije koja se sastoji od skupova iz familije 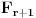 koji sadrže elemenat koji sadrže elemenat 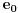 , i posmatramo familiju , i posmatramo familiju 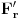 koja se dobija na taj način što iz skupova familije koja se dobija na taj način što iz skupova familije 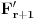 odstranimo element odstranimo element 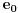 . Prema indukcijskoj hipotezi postoji skup veličine . Prema indukcijskoj hipotezi postoji skup veličine 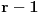 koji ima neprazan presek sa svakim skupom iz familije koji ima neprazan presek sa svakim skupom iz familije 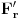 , nazovimo taj skup , nazovimo taj skup  . I sada, ako se ne varam, ti tvrdiš da je skup . I sada, ako se ne varam, ti tvrdiš da je skup 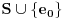 traženi skup za familiju traženi skup za familiju 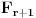 . E tu se već ne mogu složiti sa tobom, ono što mi znamo u ovom momentu je da je skup . E tu se već ne mogu složiti sa tobom, ono što mi znamo u ovom momentu je da je skup  traženi skup za familiju traženi skup za familiju 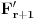 , ali i dalje ne znamo da on ima neprazan presek sa skupovima koji pripadaju familiji , ali i dalje ne znamo da on ima neprazan presek sa skupovima koji pripadaju familiji 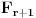 a ne pripadaju familiji a ne pripadaju familiji 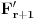 . Da li sam možda negde pogrešio u tumačenju ovog tvog rešenja? . Da li sam možda negde pogrešio u tumačenju ovog tvog rešenja?[ neor @ 16.03.2005. 07:23 ] @
Mislim da greska postoji jos ranije.
Kad izbacimo element e0 iz svih skupova podfamilije vise ne mozemo da tvrdimo da svaka dva imaju neprazan presek, a samo za takve vazi hipoteza. [ noviKorisnik @ 16.03.2005. 07:25 ] @
[ zi:: @ 16.03.2005. 08:36 ] @
[ Bojan Basic @ 16.03.2005. 11:11 ] @
Da, sad vidim da je i neorov komentar na mestu, tako da mi se čini da ovako ne može da se izgura.
Evo male pomoći: indukcija jeste ključna stvar u zadatku, ali nije baš tako trivijalna da treba da se dokaže ako važi za skupove sa  elemenata da onda važi i za one sa elemenata da onda važi i za one sa 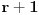 elementom. Indukcija se sprovodi nešto drugačije: treba dokazati da svako elementom. Indukcija se sprovodi nešto drugačije: treba dokazati da svako  važi jedna od dve stvari: ili važi tvrđenje zadatka (u kom slučaju smo završili), ili važi jedna druga stvar (za sada neću otkriti šta), a onda dokažemo da je nemoguće da važi ta druga stvar i to je rešenje. važi jedna od dve stvari: ili važi tvrđenje zadatka (u kom slučaju smo završili), ili važi jedna druga stvar (za sada neću otkriti šta), a onda dokažemo da je nemoguće da važi ta druga stvar i to je rešenje.[ darkosos @ 16.03.2005. 20:08 ] @
Da li bi moglo ovako: da se pokaže da postoji bar jedan skup iz familije koji sadrži bar jedan elemenat kojeg ne sadrži ni jedan drugi skup iz familije. Ideja je jednostavna: takvom skupu izbacimo taj elemenat, i to je rešenje. Naravno, izgleda da nije tako lako dokazati taj prvi deo, i pitanje je da li je uopšte tačno, mada mi nešto govori da bi u suprotnom imali kontradikciju da beskonačnošću familije.
I nekako baš golica to što svaki član familije seče sve ostale, dakle svaki je na samo korak od traženog. [ Bojan Basic @ 16.03.2005. 20:19 ] @
Citat: darkosos: Da li bi moglo ovako: da se pokaže da postoji bar jedan skup iz familije koji sadrži bar jedan elemenat kojeg ne sadrži ni jedan drugi skup iz familije. Nisam siguran, na prvi pogled ne vidim kako bi mogao to da isteraš, mada nije loša ideja. [ noviKorisnik @ 16.03.2005. 21:16 ] @
Na žalost, ne mora da postoji nijedan skup s jedinstvenim elementom da bi familija odgovarala uslovima zadatka. Evo jedne kontre:
0, 1, 2 0, 1, 3 0, 2, 3 0, 4, 5 0, 4, 6 0, 5, 6 ... [ darkosos @ 17.03.2005. 11:48 ] @
Hm, da, to je dobar primer. I razmišljao sam o tome da stavim ograničenje da ne postoji element kojeg sadrže svi članovi familije. Pitanje je da li bi ovo moglo da se izvede da nije tako. S' druge strane ako je presek svih skupova familije neprazan, onda je trivijalno postojanje traženog skupa... Probaj da nađeš kontraprimer familije sa praznim presekom. Ako i to ima, onda moja ideja definitivno pada u vodu.
Stvar je u tome da kad staviš da svi sadrže neki element, onda je veoma jednostavno napraviti beskonačnu familiju. Praktično jedino treba voditi računa o tome da ne ponoviš neku kombinaciju. Mada je pitanje preseka familije inače ovde interesantno. [ neor @ 17.03.2005. 12:55 ] @
Familija sa praznim presekom:
{0,1,2} {0,3,4} {1,3,4} {1,3,5} {1,3,6} {1,3,7} ... [ darkosos @ 17.03.2005. 17:38 ] @
Da, dodajmo tome još i
{2,3,4} {2,3,5} {2,3,6} ... i definitivno pada. Nego, nešto se razmišljam, šta kažete na ovakvu jednu ideju, to bi moglo da bude već bliže istini: 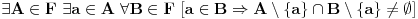 Tj., narodskim jezikom, ako se taj neki a, element A, sadrži u još nekom skupu, onda A i taj drugi skup imaju još zajedničkih elemenata. Ovo je slabiji uslov od onog prethodnog a gledajući nabrojane primere, izgleda kao da u zavisnosti od r, tj. veličine skupova, ne može biti mnogo elemenata koji će povezivati skupove. Odnosno neki su tu na neki način proizvoljni, dok drugi čine vezu između članova familije, neophodnu da bi familija imala osobinu da se dva po dva seku. [ noviKorisnik @ 17.03.2005. 22:49 ] @
Element skupa određuje particiju familije na dve klase preko relacije pripadanja skupu familije.
Ako je kojim slučajem jedna klasa bez skupova, to govori da element pripada svim skupovima, pa tu imamo trivijalno rešenje - proizvoljni skup odgovarajuće veličine koji sadrži taj element. Netrivijalni slučaj je da postoje i skupovi koji ne sadrže taj element. Ali zato svaki od njih sadrži bar jedan od preostala r - 1 elementa prvoposmatranog skupa. Itd... Mala ilustracija za r = 3: (ako je 0, 1 rešenje) skupovi s nulom skupovi s jedinicom bez nule skupovi s dvojkom bez jedinice i bez nule - ovaj bi trebalo da bude prazan, e sad pogodi zašto [ gpreda @ 18.03.2005. 07:27 ] @
Bojane, daj jos neku pomoc ili resenje.
[ noviKorisnik @ 18.03.2005. 07:35 ] @
Citat: Bojan Basic: Odmah ću da kažem da se zadatak rešava bukvalno iz dva koraka, nikakav "Rat i mir" nije potreban. Možda bi dobar hint bio prvi korak... [ Bojan Basic @ 18.03.2005. 12:12 ] @
Pošto neću biti tu narednih par dana a zaista ne umem da smislim neki "odmeren" hint koji ne bi rekao sve ali bi ipak pomogao (zapravo, jedan sam postavio, http://www.elitesecurity.org/poruka/667448, ali izgleda da niko nije shvatio šta je pisac hteo da kaže), napisaću sad celo rešenje.
Neka je data familija čiji članovi imaju po  elemenata. Dokazaćemo sledeće: ako je elemenata. Dokazaćemo sledeće: ako je  skup takav da je skup takav da je 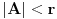 koji je sadržan u beskonačno mnogo skupova iz familije koji je sadržan u beskonačno mnogo skupova iz familije  , onda važi da ili , onda važi da ili  ima neprazan presek sa svakim skupom iz familije ima neprazan presek sa svakim skupom iz familije  (u tom slučaju smo završili), ili postoji neki element (u tom slučaju smo završili), ili postoji neki element 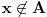 takav da je takav da je 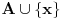 sadržan u beskonačno mnogo skupova iz familije sadržan u beskonačno mnogo skupova iz familije  . Pošto jedan takav skup očigledno postoji (npr. . Pošto jedan takav skup očigledno postoji (npr. 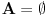 ), ako dokažemo ovu tvrdnju onda njenom uzastopnom primenom ), ako dokažemo ovu tvrdnju onda njenom uzastopnom primenom  puta dobijamo to što se traži (jer skup veličine puta dobijamo to što se traži (jer skup veličine  sigurno ne može biti sadržan u beskonačno mnogo skupova iz naše familije). Da bismo dokazali tvrdnju, pretpostavimo da neki skup sigurno ne može biti sadržan u beskonačno mnogo skupova iz naše familije). Da bismo dokazali tvrdnju, pretpostavimo da neki skup 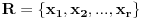 iz date familije nema zajedničkih elemenata sa skupom iz date familije nema zajedničkih elemenata sa skupom  . Svaki od onih beskonačno mnogo skupova koji sadrže . Svaki od onih beskonačno mnogo skupova koji sadrže  ima neprazan presek sa ima neprazan presek sa  , znači neko , znači neko  iz iz  se sadrži u beskonačno mnogo takvih skupova, iz čega sledi da možemo uzeti se sadrži u beskonačno mnogo takvih skupova, iz čega sledi da možemo uzeti 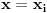 . Ovim je dokaz završen. . Ovim je dokaz završen.Nadam se da se oni što su želeli još malo da razmisle ne ljute što sam odmah objavio celo rešenje. U svakom slučaju, ako ste zainteresovani imate nekoliko svežih zadataka različite težine u http://www.elitesecurity.org/poruka/667144, a kao i do sada ću s vremena na vreme postavljati slične mozgalice. [ darkosos @ 05.04.2005. 08:55 ] @
Šta znači da je jedan skup sadržan u drugom? Pretpostavljam da misliš na inkluziju?
[ Bojan Basic @ 05.04.2005. 14:04 ] @
Da, inkluzija ili podskup.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|