Ako pođemo od
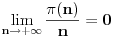
(ovo sledi iz poznate asimptotske jednakosti J.S.Hadamard-a i C. de la Vallee Poussin-a, a može se dokazati i posebno), onda za svako
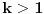
postoji minimalno
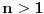
za koje važi
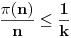
. Pretpostavimo da nije
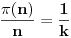
, onda mora biti
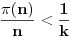
, a zbog minimalnosti broja

važi i
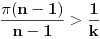
, sada iz prve nejednakosti sledi
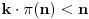
a iz druge
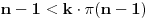
tj.
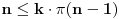
, pa dobijamo
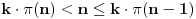
tj.
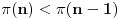
što je očigledno kontradikcija, dakle, mora biti
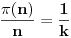
tj.
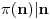 [Ovu poruku je menjao uranium dana 15.08.2005. u 16:30 GMT+1]
[Ovu poruku je menjao uranium dana 15.08.2005. u 16:30 GMT+1]