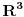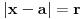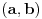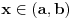[ Humanoid @ 20.03.2005. 10:41 ] @
| Za početak,nije mi jasna definicija otvorenog skupa.Razumijem definicju otvorene kugle,ali ne i sljedeće: Skup Omega(Podskup od R^n) je otvoren ako oko svake svoje točke sadrži otvorenu kuglu kojoj je ta točka središte. E pa,nije mi jasno,recimo,što bi bilo kad bih ja došao do neke rubne točke nekog skupa,kako oko nje naći otvorenu kuglu?Prema tome onda i nema otvorenih skupova.Znam da tu negdje griješim,a gdje točno? Zasad je to to(bit će još:-) |