Posto tema vec dugo vremena nema odgovora (a meni nikako ne uspeva da nadjem resenje), da li bi ti Bojane mogao da das resenje?

Nema problema, ja sam mislio da niko nije zapazio nejednakost pa zbog toga nisam žurio sa rešenjem (ko zna, možda neko nekad pregleda forum pa mu zapadne za oko ova tema bez odgovora :), ali evo kad te interesuje:

Prvi korak nije naročito elegantan, izmnožimo sve i pokratimo pa dobijemo da je data nejednakost ekvivalentna sa

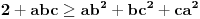
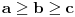
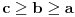
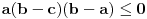
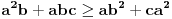
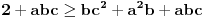
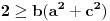
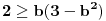
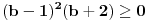
Pretpostavimo da je "srednja" od ove tri promenljive (odnosno da je ili ). Onda je očigledno , što je ekvivalentno sa . Dakle, dovoljno je dokazati , odnosno tj. . Međutim, poslednja nejednakost je ekvivalentna sa , što je očigledno tačno.

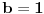
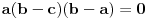
Zanimljiv je slučaj kad važi jednakost. Za početak, iz poslednje relacije očigledno sledi . Međutim, važi u dva slučaja, tako da imamo dva slučaja kada važi jednakost (ne računajući permutacije):
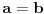
1) , odnosno ;
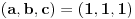
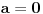
2) , odnosno .

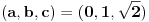
Lepo resenje.
U medjuvremenu, nasao sam jos dva resenja na jednom sajtu :), ali je ovo mnogo elegantnije.