Mora da sam pogresio pri negaciji jer je ovo ispalo suvise jednostavno ali ipak evo mog pokusaja:
Pretpostavimo da ne postoji takav skup A.
To znaci da za svaki skup A i svaki beskonacan skup prostih brojeva S, svi proizvodi k razlicitih elemenata iz S su u A ili ni jedan nije u A.
Za ovo se moze napraviti kontraprimer. Neka je S skup svih prostih brojeva, A skup svih parnih brojeva. Svi proizvodi sa 2 su u A a oni bez 2 nisu u A.
To je kontradikcija sa pretpostavkom pa znaci da postoji takav skup A.

Mislim da nisi u pravu. Tacna negacija je 'za svako A, postoji S'.

Neka je skup prostih brojeva (u uredjenom rasporedu, je i-ti prost broj).

Skup A mozemo konstruisati na sledeci nacin:


(odnosno, skup sadrzi sve kombinacije proizvoda k prostih brojeva, osim onih koje sadrze k-ti prost broj)


Skup A zadovoljava trazena svojstva.

Dokaz: ako je S proizvoljan beskonacni skup prostih brojeva, (gde su uredjeni), tada:
ne pripada skupu A, dok
pripada skupu A
(k je takvo da je , tj. je k-ti prost broj).

Dobro je, sviđa mi se ideja.

Rešenje koje ja imam je dosta slično mada se ipak razlikuje u nekim tačkama tako da mislim da ne bi bilo zgoreg da ga napišem.

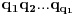
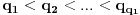
Neka je skup prirodnih brojeva oblika , gde su prosti brojevi. Drugim rečima



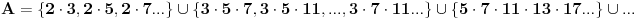
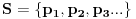
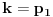
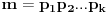
Za proizvoljan beskonačan skup prostih brojeva , postavljeni uslov zadovoljavaju brojevi , i .
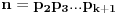