[ Bojan Basic @ 04.04.2005. 23:38 ] @
|
[ ImPlant @ 05.04.2005. 12:42 ] @
veoma lep zadatak i super formulisan :)
[ Bojan Basic @ 05.04.2005. 13:54 ] @
[ qzqzqz @ 06.10.2007. 10:25 ] @
Ja cu da dokazem 2D slucaj datog zadatka, a ko zna neka uopsti. Znaci treba pokazati da se za dati jednakostranican trougao ABC i tacke M i N na stranicama AB, AC od duzi CN, BM i MN moze sastaviti trougao. Uochimo tacku D takvu da je ABCD pravilan tetraedar. Onda je DM=CM i DN=BN, pa je trougao DMN trazeni.
[ bata kg @ 24.01.2009. 19:20 ] @
neobican zadatak, posebno jer je opsti pa i resenje mora biti opste. ako se jos uvek nalazi na listi neresenih znaci li to da jos uvek niko nije prijavio resenje.sta da radim sa resenjem.
od skoro sam na netu,mozda je glupo, izvinjavam se unapred. [ Bojan Basic @ 24.01.2009. 20:10 ] @
Na listi nerešenih zadataka nalaze se zadaci koji nisu rešeni na ovom forumu. To ne znači da rešenje takvih zadataka niko nikad nije pronašao, samo ga niko nije ovde ponudio.
Ako imaš rešenje, slobodno ga napiši ovde, pa ćemo ga analizirati. Ako i nemaš rešenje ali imaš neke ideje, ili bilo šta slično vezi s ovim zadatkom o čemu bi hteo da porazgovaraš s ostalim članovima foruma, slobodno i to iznesi. Drugim rečima, tema je otvorena za bukvalno bilo šta što ima veze s postavljenim zadatkom. [ barum @ 25.01.2009. 11:12 ] @
Citat: Duž MN može biti stranica trouglova: MNA, MNB, MNC ili MND. Duž BN može biti stranica trouglova: BNA, BNC, MND ili BNM. Duž MD može biti stranica trouglova: MDA, MDB, MDC ili MDN. Sve su to neki trouglovi. Ali ako se želi dokaz da su to stranice ISTOG trougla onda, pošto su M i N različite tačke, može da se dokaže da MNBD ni u kom slučaju ne može da bude trougao. [ bata kg @ 25.01.2009. 11:30 ] @
najmanje duzine BN i DM su jednake visinama tacaka B i D. Bilo koja tacka van njih rezultuje vecim duzima. Spustimo tacke B i D u tacku preseka njihovih visina. Ova tacka( na podjednakom rastojanju u odnosu na tacke B i D) i tacke N i M bilo gde cine trougao. Trougao egzistira i povecanjem dveju njegovih stranica za isti iznos( smanjene spustanjem).
hvala na razumevanju i iscrpnom odgovoru [ Bojan Basic @ 25.01.2009. 15:04 ] @
Citat: barum: Duž MN može biti stranica trouglova: MNA, MNB, MNC ili MND. Duž BN može biti stranica trouglova: BNA, BNC, MND ili BNM. Duž MD može biti stranica trouglova: MDA, MDB, MDC ili MDN. Sve su to neki trouglovi. Jesu, ali treba pokazati da su sve tri duži stranice nekog, jednog trougla, a ne da svaka ima „svoj“ trougao. Citat: barum: Ali ako se želi dokaz da su to stranice ISTOG trougla onda, pošto su M i N različite tačke, može da se dokaže da MNBD ni u kom slučaju ne može da bude trougao. Da, želi se dokaz da su to stranice istog trougla, ali je dozvoljeno duži pomerati. Drugim rečima, treba dokazati da se od njih može formirati trougao, kao što je već i pojašnjeno ovde. Citat: bata kg: Trougao egzistira i povecanjem dveju njegovih stranica za isti iznos( smanjene spustanjem). Ovde se nalazi greška. Kada „vratimo“ tačke na polazne pozicije, one su zaista prešle isti put tokom tog vraćanja, ali to ne znači i da su se dužine stranica povećale za međusobno isti iznos. Lako je moguće čak i da se obe stranice smanje, kao i da se jedna poveća a druga smanji, i sl. Citat: bata kg: hvala na razumevanju i iscrpnom odgovoru Nema na čemu. [ bata kg @ 25.01.2009. 17:07 ] @
bilo koja "skracena" BN(DM) se moze smatrati nekom vrstom projekcije( ugao nije 90 vec nesto veci) "neskracenih" BN(DM). Odatle "skracene" se uvek uvecavaju. Primedba da se nejednako povecavaju stoji, ali "spustanje" u zajednicku tacku i ne mora biti podjednako. Vazno je da se uvek moze naci takva tacka koja daje jednako povecanje.
[ barum @ 25.01.2009. 17:43 ] @
Ali u tri duži učestvuju četiri različite tačke (M, N, B i D) i pošto su različite nema govora o trouglu. Čak nema govora ni o četvorouglu pošto nisu komplanarne. Najverovanije je neka greška i da se radi ipak o tri tačke jer stranica trougla spaja dva temena inače nije stranica trougla. Ili ja ne razumem pojam apstrakovanja (zanemarivanje nebitnog).
[ Bojan Basic @ 25.01.2009. 18:45 ] @
Citat: bata kg: bilo koja "skracena" BN(DM) se moze smatrati nekom vrstom projekcije( ugao nije 90 vec nesto veci) "neskracenih" BN(DM). Odatle "skracene" se uvek uvecavaju. I dalje smatram da nisi u pravu. Nisam baš siguran na kakvu projekciju misliš, ali u svakom slučaju projekcija pod uglom različitim od 90º može biti duža od originala, što ne bi mogla? Citat: barum: Ali u tri duži učestvuju četiri različite tačke (M, N, B i D) i pošto su različite nema govora o trouglu. Trougao se sastoji od tri duži (zato se tako i zove), a tebi su ovde ponuđene upravo tri duži. Pitanje je možeš li od njih sklopiti trougao ili ne možeš. Niko ne kaže da te duži moraju ostati na svom mestu (što sam već rekao). Ako bih ti stavio na sto tri šibice i pitao možeš li da sastaviš trougao od njih, da li bi možda rekao kako ne možeš zato što se jedna šibica nalazi na jednom kraju stola, a druga na drugom? [ barum @ 25.01.2009. 20:43 ] @
Citat: Bojan Basic: Trougao se sastoji od tri duži (zato se tako i zove), a tebi su ovde ponuđene upravo tri duži. Pitanje je možeš li od njih sklopiti trougao ili ne možeš. Niko ne kaže da te duži moraju ostati na svom mestu (što sam već rekao). Jesu li to vektori ili duži? Nigde nije pomenuto da se ne mogu rotirati ni skalirati niti translatovati. Izgleda da je zadatak glupo formulisan i da nema veze šta je rečeno pošto je važnije šta nije. Znači sve što nije rečeno može? citiram: "M i N, različite tačke u ravnima ABC i ADC, redom" Da li te transformacije nad dužima mogu da dovedu do toga da M i N ne moraju da budu različite tačke? Citat: Bojan Basic: Ako bih ti stavio na sto tri šibice i pitao možeš li da sastaviš trougao od njih, da li bi možda rekao kako ne možeš zato što se jedna šibica nalazi na jednom kraju stola, a druga na drugom? :) Da li to znači da iako je rečeno da M pripada ABC "kraju stola" ne mora tu i da ostane već je slobodno? Sada vidim da zadatka nije ni bilo. [ zzzz @ 25.01.2009. 21:10 ] @
Bojan: Neka je ABCD pravilan tetraedar i M,N različite tačke u ravnima ABC i ADC, redom. Pokazati da su duži MN, BN i MD stranice nekog trougla.
Mala pomoć: pročitati naslov teme :) Znači li to da: Od navedenih stranica se uvjek može sklopiti trougao. A tačke M i N mogu ležati čak i izvan tetraedra u odgovarajućoj ravni? Ako je tako onda treba dokazati da najveća stranica nije duža od zbira druge dvije. Mislim da bi rješavanje išlo preko vektora, zatvaranjem poligona pomoću ivica tetraedra, AB,BC,CD. Jesam li zalutao? [ Bojan Basic @ 25.01.2009. 21:45 ] @
Citat: barum: Da li te transformacije nad dužima mogu da dovedu do toga da M i N ne moraju da budu različite tačke? Ne. Tačke  i i  određuju pomenute duži, i na te tačke ne možeš uticati — takve su kakve su. E sad, kad dobiješ duži, onda ih možeš „iščupati“ iz tetraedra i negde sa strane od njih formirati trougao. određuju pomenute duži, i na te tačke ne možeš uticati — takve su kakve su. E sad, kad dobiješ duži, onda ih možeš „iščupati“ iz tetraedra i negde sa strane od njih formirati trougao.Citat: barum: Da li to znači da iako je rečeno da M pripada ABC "kraju stola" ne mora tu i da ostane već je slobodno? Vidi gore. Citat: barum: Sada vidim da zadatka nije ni bilo. Razni ljudi su se već uveliko uključilo u rešavanje zadatka (bata kg je ponudio jedno rešenje pa sad ispitujemo je li korektno, i zzzz razmatra jedan pristup, a još je odavno qzqzqz rešio nešto slično, samo u dve dimenzije), pa ova tvoja izjava da „zadatka nije ni bilo“ ne deluje baš smisleno (a ni kulturno prema tim ljudima). Citat: zzzz: Znači li to da: Od navedenih stranica se uvjek može sklopiti trougao. A tačke M i N mogu ležati čak i izvan tetraedra u odgovarajućoj ravni? Upravo tako. Citat: zzzz: Mislim da bi rješavanje išlo preko vektora, zatvaranjem poligona pomoću ivica tetraedra, AB,BC,CD. Jesam li zalutao? Rešenje koje ja imam ne koristi vektore. Zapravo, imam dva rešenja, od koje je jedno ono „apstraktno“ iz naslova, dok je drugo prizemnije(i dosadnije); nebitno, nijedno od njih ne koriste vektore. No, to svakako ne znači da je nemoguće rešiti zadatak preko vektora — probaj, pa ako uspeš, super. [ barum @ 25.01.2009. 23:21 ] @
Dobro, tek sam sada shvatio, izgleda da sporo kapiram.
Dakle, potrebno je dokazati da dužine MN, BN i MD mogu biti dužine stranica nekog trougla. [ zzzz @ 26.01.2009. 01:18 ] @
MN stranica ne smije biti veća od zbira niti manja od razlike druge dvije stranice.
MD+NB > MN i MD-NB < MN -------------------------- Za zadane tačke M i N uočimo njihove udaljenosti od težišta tetraedra T, MT i NT. MN je najveće kada se te dvije udaljenosti saberu.(MN=MT+NT) MN je najmanje kad se od veće udaljenosti oduzme manja.(MN=MT-NT) --------------------------- Zbog MD > MT i NB > NT MD + NB > MT + NT MD + NB > MN ispunjen prvi uslov. --------------------------- sl.1) 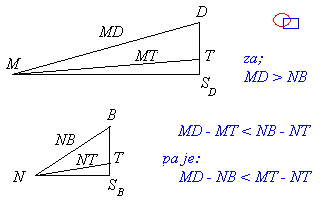 Zbog MD - MT < NB - NT MD - NB < MT - NT MD - NB < MN ispunjen i drugi uslov. [ bata kg @ 26.01.2009. 13:00 ] @
tvoje primedbe su na mestu. Citajuci tvoje primedbe i moja obrazlozenja koja su puna nekih "mojih" izraza, uvidjam da je malo problem u komunikacijama. Verovatno sve to deluje strasno uprosceno ali to je samo rezultat a ne postupak(lutanja i trazenja) resenja. Tvoje sugestije su ipak (cinimi se) teoretske.
Da probam ovako: Ortogonalna projekcija tacke B na ravan ACD daje tacku N i stim i najkracu duz BN. Ako je N bilo gde u datoj ravni duz BN ce uvek biti duza od od svoje o.projekcije, pa na kraju i od svake "B"N duzi( tacka "B" se nalazi negde ispod tacke B na njenoj o.projekciji tj. visini). Naknadnim "vracanjem" duzi "B"N na BN ista se samo uvecava. Sve ovo vazi i za duz DM. Ostaje samo naci zajednicku tacku X tacaka D i B, naravno nize od njihovih visina(XM i XN su krace od odgovarajucih DM i BN) Dobijamo trougao XNM. Tacno je da je produzenje duzi isto samo kad su i duzi BN i MD iste, ali zajednicka tacka X nije striktno na istoj udaljenosti od tacke B i D. Ona samo ispunjava uslov da pri "vracanju" ne rusi egzistenciju trougla( da ne nabrajam uslove). Uvecanje dveju stranica na kraju krajeva i ne mora biti podjednako, vazno je da on egzistira. Kako odrediti tacnu poziciju tacke X nije ovde bitno, ali se sigurno uvek moze odrediti. Nadam se da sam sada malo jasniji. Iz tvojih odgovora vidim da imas dosta razumevanja za nas sagovornike koji ponekad i malo vise skrenemo sa teme. Svaka cast. Jedno pitanje? Kako da nacrtam neki geometrijski crtez, to bi ustedelo mnogo reci? Unapred hvala. [ galet@world @ 27.01.2009. 20:57 ] @
Ja bih to rešio ovako: Projektovao bih tačku M i N na bazu tetraedra i nacrtao projekcije dužina NB i MD Projekcije tačaka su M' i N', a dužina N'B i M'D kao i projekciju M'N' Sada bih zarotirao tačku B oko osovine NN' u ravni baze tetraedra i to isto bih uradio i sa tačkom D oko osovine MM' - tamo gde se te kružnice seku bio bi treći vrh O trougla MNO Treba dokazati da će se kružnica sa radiusom M'D seći sa kružnicom radiusa N'B. Za ekstremne vrednosti kraća projekcija ne može biti manja od 2/3 visine baze kao jednakostraničnog trougla, a duža ne može biti veća od strane trougla - i u slučaju kad su obe projekcije najkraće a i u slučaju kad su obe projekcije najduže - kružnice sa tim radiusima će se seći što nije teško dokazati u ravni jednakostranične baze tetraedra. Ako smo dokazali da se projekcije seku u tački O u ravni baze onda se tu seku i stvarne dužine jer tačke B, D i O su u ravni projekcije. Rotacijom projekcija dužina ne menjamo ni malo projektovane dužine. Sve bi ovo trebalo nacrtati, ali neka to uradi neko ko bolje crta. Znam da se ne izražavam baš najbolje, ali ako sam dobro rešio onda će to Bojan bolje objasniti. [Ovu poruku je menjao galet@world dana 27.01.2009. u 23:43 GMT+1] [ zzzz @ 28.01.2009. 00:49 ] @
Evo te skice Dane:
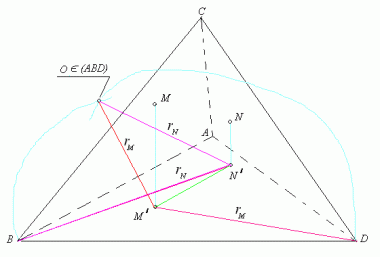 Ali već je rečeno: ja Znači li to da: Od navedenih stranica se uvjek može sklopiti trougao. A tačke M i N mogu ležati čak i izvan tetraedra u odgovarajućoj ravni? Bojan: Upravo tako. A onda nastaju problemi jer se lukovi ne moraju sjeći, a rješenje ipak postoji. [ galet@world @ 28.01.2009. 08:28 ] @
Evo i moje slike i malo grubljeg dokaza pa neka presudi Bojan [ bata kg @ 28.01.2009. 18:02 ] @
Dane-lepo sroceno.
Milan-lepo nacrtano. Ako biste umesto pokretnih tacaka M i N uzeli tacke B i D bilo bi sve mnogo prostije i bez ikakvih ogranicenja. Spojite tacke B i D u tacki X(presek njihovih visina)..... Jos uvek ne znam kako da nacrtam crtez! [ Bojan Basic @ 28.01.2009. 18:45 ] @
Citat: zzzz: Zbog MD - MT < NB - NT Nisam uspeo da zaključim odakle si ovo dobio. Citat: bata kg: Ostaje samo naci zajednicku tacku X tacaka D i B, naravno nize od njihovih visina(XM i XN su krace od odgovarajucih DM i BN) Dobijamo trougao XNM. Tacno je da je produzenje duzi isto samo kad su i duzi BN i MD iste, ali zajednicka tacka X nije striktno na istoj udaljenosti od tacke B i D. Ali ako tačke „spuštamo“ po odgovarajućim visinama, jedino meste gde se te visine seku upravo je centar tetraedra. Dakle, jedini način da tačke  i i  spustimo u istu tačku jeste da ih obe spustimo do centra, a ranije smo videli da to ne mora uvek valjati. Zar ne? spustimo u istu tačku jeste da ih obe spustimo do centra, a ranije smo videli da to ne mora uvek valjati. Zar ne?Citat: bata kg: Jedno pitanje? Kako da nacrtam neki geometrijski crtez, to bi ustedelo mnogo reci? Unapred hvala. Crtež nacrtaš u svom omiljenom programu za crtanje, a ovde ga samo ubaciš kao sliku (ovde je opisano kako). Citat: galet@world: Za ekstremne vrednosti kraća projekcija ne može biti manja od 2/3 visine baze kao jednakostraničnog trougla, a duža ne može biti veća od strane trougla Ovde je greška. Tačke  i i  ne moraju nužno da pripadaju stranama ne moraju nužno da pripadaju stranama  i i  ; one su bilo gde u odgovarajućim ravnima (tj. mogu da budu i van tetraedra), pa ova ograničenja ne važe. ; one su bilo gde u odgovarajućim ravnima (tj. mogu da budu i van tetraedra), pa ova ograničenja ne važe.Citat: galet@world: Evo i moje slike i malo grubljeg dokaza pa neka presudi Bojan Fina skica. Samo, ne mogu ja ovde da budem nikakav sudija. Matematika je egzaktna nauka, i u rešenju nekog problema svaki korak mora da bude čvrsto utemeljen. Ako jeste, onda je dokaz korektan, bez obzira na to da li se možda nekom ne sviđa (i obrnuto, ako je neki korak sumnjiv, ne može se preći preko toga). Ja ovde samo skrećem pažnju na neke korake za koje mislim da nisu dovoljno jasni. Ako sam u pravu, i rešavač će shvatiti grešku i pokušati da je koriguje; ako je pak on u pravu, dodatno će objasniti sporni korak, pa ćemo zaključiti da rešenje ipak jeste korektno. Kako god bilo, ne možemo ignorisati tačno rešenje zato što ja tako kažem, niti prihvatati pogrešno zato što ja tako kažem. [ galet@world @ 28.01.2009. 21:29 ] @
Citat: Bojan Basic:Ovde je greška. Tačke M i N ne moraju nužno da pripadaju stranama ABC i ACD i ; one su bilo gde u odgovarajućim ravnima (tj. mogu da budu i van tetraedra), pa ova ograničenja ne važe. I jeste greška jer zadatak ovako glasi: Citat: Neka je ABCD pravilan tetraedar i M, N različite tačke u ravnima ABC i ADC, redom. Pokazati da su duži MN , BN i MD stranice nekog trougla. Svak živ će shvatiti da tačke M i N pripadaju tetraedru ABCD pa čak i u odgovoru barumu stoji: Citat: Ne. Tačke M i N određuju pomenute duži, i na te tačke ne možeš uticati — takve su kakve su. E sad, kad dobiješ duži, onda ih možeš „iščupati“ iz tetraedra i negde sa strane od njih formirati trougao. Šta da "išupa" iz tetraedra kad po ovoj novoj definiciji zadatka ni jedna od tri duži ne mora ni da pripada tetraedru ABCD? (Zar je bilo teško napisati u zadatku da se tačke M i N nalaze negde u ravnima koje su definisane tačkama ABC i ADC?) Citat: Samo, ne mogu ja ovde da budem nikakav sudija To nisam ni mislio - bila je to samo figurativna fraza. P. S. Ako tačke M i N pripadaju tetraedru onda sam dao rešenje i mogu i da ga dokažem, a osim toga ovo je deo rešenja zadatka i po ovoj novoj definiciji jer ni nova definicija ne zabranjuje da tačke M i N pripadaju tetraedru. [ Bojan Basic @ 28.01.2009. 22:36 ] @
Citat: galet@world: (Zar je bilo teško napisati u zadatku da se tačke M i N nalaze negde u ravnima koje su definisane tačkama ABC i ADC?) Pogledaj prvu poruku na temi, koju si upravo i sam citirao: Citat: Ravan je, kao što kažeš, definisana sa tri tačke, i ovde je određeno o kojoj ravni je reč navodeći tri tačke (tj. dva puta po tri tačke, budući da govorimo o dve ravni). Citat: galet@world: P. S. Ako tačke M i N pripadaju tetraedru onda sam dao rešenje i mogu i da ga dokažem, a osim toga ovo je deo rešenja zadatka i po ovoj novoj definiciji jer ni nova definicija ne zabranjuje da tačke M i N pripadaju tetraedru. Jeste deo zadatka, to nisam osporavao (s tim što nema nikakve „nove“ definicije, jer je to određeno već u prvoj poruci, kao što sam upravo naveo). [ zzzz @ 29.01.2009. 09:37 ] @
Bojan: Nisam uspeo da zaključim odakle si ovo dobio.
MD-MT<NB-NT (Na onoj slici sam naveo da to vrijrdi za MD>NB) A evo i zašto. Izrazimo ovu razliku (MD-MT) kao funkciju udaljenosti tačke M od podnožja visine.Na slici to je duž MS(d),dok je duž DS(d) visina tetraedra.Koristićemo Pitagorin poučak.Analizirajmo ovu funkciju za 0<x<beskonačno.Za x=0 vrijednost je jednaka udaljenosti vrha od težišta tetraedra.Prvi izvod ove funkcije je uvijek negativan što znači da je funkcija monotono opadajuća na cijelom domenu.Imamo horizontalnu asimptotu y=0.Odatle zaključak da za x1>x2 vrijedi f(x1)<f(x2). 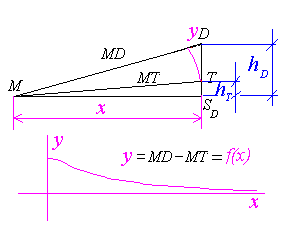 [Ovu poruku je menjao zzzz dana 29.01.2009. u 11:03 GMT+1] [ bata kg @ 01.02.2009. 18:18 ] @
Slika 1.Tacke M i N spojimo sa tackom X(presek visina).
Slika 2i3.Visina tacke D(B)na ravan ABC(ACD)i polozaj tacke X i N(M). Slika 4.Poshto su visina tacaka D i B iste,spojimo ova dva preseka.Bitno je da DN,NX,BM i XN ostaju nepromenjene kao na slici 1. Slika 5.Kruznim lukovima dobijamo razlike duzi ND-NX i MB-MX. Slika 6.Prikaz razlika sa slike 5.Prava B daje isti odsecak sa levom stranom a prava a deli razliku na iste vrednosti. Slika 7.Duz NX se skracuje i postaje NS,a MX se uvecava i postaje MS(tacka s se dobija presekom lukova).Skracenje i uvecavanje na osnovu slike 6.Tacka S sa MN(bilo gde da su) cine trougao.Povecanjem duzi NS i MS za isti iznos dobijamo duzi ND i MB nepromenjene u odnosu na sliku 1.Trougao i dalje egzistira. 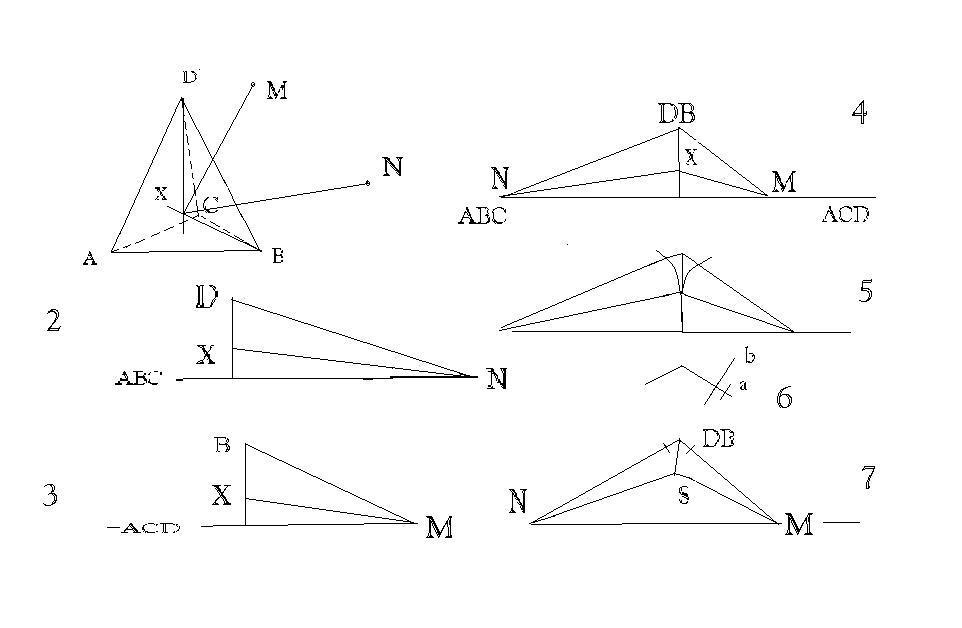 [Ovu poruku je menjao bata kg dana 01.02.2009. u 19:29 GMT+1] [ zzzz @ 07.02.2009. 09:45 ] @
Dokaz da razlika udaljenosti tačaka od odgovarajućih vrhova tetraedra mora biti
manja od razlike udaljenosti tih tačaka od težišta napravio sam analitički. Zadatak je euklidski pa je analitički dio dokaza u neskladu sa ostalim dijelom. Probaću to dokazati kao što bi to radio Euklid.U njegovo vrijeme nije bio poznat pojam prvog izvoda i tih stvari. Dakle želim dokazati da za dane tačke M i N tj njihove udaljenosti od vrhova MD i NB (ma kako bile raspoređene ove tačke) nemogu imati razliku veću od duži MN. A Već sam ranije postavio dvije koncentrične kugle sa centrima u težištu tetraedra (T) i sa radijusima MT I NT.Kako tačke M i N leže na kuglama njihova najmanja udaljenost može biti jednaka razlici radijusa MN(min)=MT-NT.Da bi se trougao mogao nacrtati mora MN(min)>MD-NB. Napravimo dva euklidska aksioma koja ne treba dokazivati: a)Tačka na kružnici koja je najbliža datoj tački izvan kružnice nalazi se na na sjecičtu kružnice i pravca koji prolazi kroz datu tačku i centar kružnice.Sve ostale tačke na kružnici su udaljenije. b)Svaka tačka koja se nalazi izvan kruga ima veću udaljenost od centra kruga nego što su to tačke na kružnici. Na slici je prikazan dokaz zasnovan na ovom. 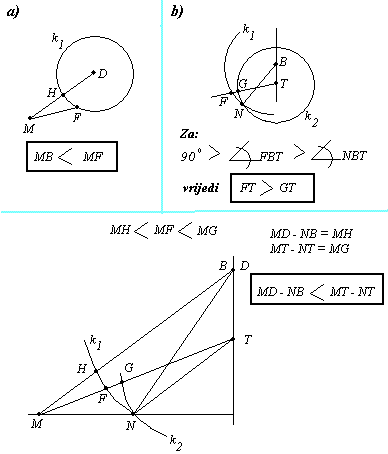 [ galet@world @ 07.02.2009. 10:19 ] @
Evo i mog pokušaja
Ispravka: Ugao MFN na mestu gde je nacrtan iznosi najmanje oko 1100 [Ovu poruku je menjao galet@world dana 07.02.2009. u 20:12 GMT+1] [ bata kg @ 07.02.2009. 20:56 ] @
Dosta interesantni pristupi resavanju problema, ipak za moj ukus dosta robusni. Pitanje je koliko njih ce razumeti resenje. Resenja moraju biti elegantna i prosta, i sa sto manje "teske artiljerije".
Samo osnovno "trougao i sestar"! [ galet@world @ 08.02.2009. 16:57 ] @
Citat: bata kg: Pitanje je koliko njih ce razumeti resenje. Resenja moraju biti elegantna i prosta, i sa sto manje "teske artiljerije". U redu je to, ali ipak ne treba zaboraviti naslov teme. Treba videti stvari u prostoru a to nije baš ni lako ni jednostavno. Evo ja sam to u principu pokušao malo jasnije prikazati P S Primetio sam na slici da se ne vide indeksi kod slova C. Kliknite na ta slova i malo povećajte box-ove udesno [Ovu poruku je menjao galet@world dana 08.02.2009. u 18:15 GMT+1] [ bata kg @ 10.02.2009. 17:12 ] @
Moram priznati da kad ti nesta pojasnis tu vise nista nema da se doda. Svaka cast na preciznosti, posebno na trudu da se to crtezom prikaze.
Moji crtezi ispadaju bas drljavo, radim ih u paintu pa nije ni cudo. Nesta nema Bojana da presudi! [ Bojan Basic @ 10.02.2009. 17:39 ] @
Citat: bata kg: Nesta nema Bojana da presudi! Ja se izvinjavam, nešto sam u gužvi ovih dana, a vidim da ima puno prilaza koje bih natenane da izanaliziram. U svakom slučaju, stići će komentar za koji dan. [ malada @ 16.02.2009. 03:02 ] @
Evo i jedno moje rijesenje, nisam crtao jer ne vijerujem u dokaze sa crteza, ali sam sve detaljno pokazao tako da se moze rekonstruisati na osnovu toga. Samo da napomenem da sam u sred ispitnog roka i da mi je ovaj zadatak oduzeo poprilicno vremena, tako da ste vi krivi ako padnem ispit ;)
Ideja je da dokazem da ce SFERE K[M,MD] i K'[N,NB] imati zajednicki presijek, a to povlaci da uzimajuci proizvoljnu tacku presijeka ove dvije sfere (Z) i spajajuci je sa M i D dobijamo trougao MNZ cije su duzine upravo MZ=MD, NZ=NB i MN=MN. Da imaju zajednicki presijek cemo pokazati tako sto dokazemo da je MD=>MB tada (zatvorena) lopta odredjena sa K sadrzi tacku B a (zatvorena) lopta odredjena sa K' po definiciji sadrzi tacku B dakle imaju zajednicki presijek. Dakle poenta je dokazati da je MD=>MB. Posmatrajmo sada konveksni prostorni odredjen sa dvije ravni P i Q koje su (respektivno) odredjene tackama ABC i ADC. Neka je a presijecna prava ravni P i Q tj prava odredjena tackama A i C. Neka je a' prava ravni P koja je paralalna sa a i sadrzi tacku B. Neka je R ravan odredjena sa pravom a' i tackom D. Sada imamo 3 slucaja: 1. Bar jedna tacka, ne umanjujuci opstost neka to bude M, se nalazi u zatvorenoj poluravni ravni P u kojoj se NE nalaze tacke A i C a na cijoj se granici nalazi tacka B. 2. Bar jedna tacka, ne umanjujuci opstost neka to bude M, se nalazi u "traci" koja pripada ravni P, a odredjena je sa pravom a i a' 3. Obadvije tacke se nalaze u poluravnima koje su preostale kada iskljucimo prva 2 slucaja. Rijesenje prvog slucaja: Ako je tako onda je ugao DBM ocigledno tup (u najgorem slucaju prav) pa je stranica naspram njega najduza stranica trougla MDB tj MD>DB i ono sto smo htijeli da dokazemo: MD=>MB. Dakle prvi slucaj je dokazan. U drugom slucaju, neka je M proizvoljna tacka iz "trake". Neka je F srediste AC. Sada je trougao DFB jednakokraki pri cemu su DF i BF visine stranica tetraedra a DB stranica tj. DB>DF i DB>BF. Neka je M' normalna projekcija tacke M na duz FB. Sada treba pokazati da je MD>MB. Posmatrajmo trouglove MM'D i MM'B oba su pravougla i imaju zajednicku stranicu MM'. Ako pokazemo da je M'D>M'B onda iz toga slijedi da je i MD>MB. Da bi smo to pokazali Posmatrajmo jednakokraki trougao DFB. Tacka M'se nalazi na duzi FB. Kako se M' nalazi na duzi FB ugao M'FB je manji od ugla M'BF pa kako se naspram veceg ugla nalazi veca stranica to je M'D>M'B te je, na osnovu razmatranja sa pocetka, i drugi slucaj (do duse "na silu") dokazan. A u trecem slucaju cemo pokazati da obadvije kugle (odredjene sa K i K') sadrze tacku F koja je srediste stranice AC. Neka je M proizvoljna tacka iz treceg slucaja. Uocimo trougao MFD. Ugao kod tijemena F je veci ili jednak od 120 stepeni te je stranica naspram njega, ocigledno, najduza tj MD>MF slijedi F pripada K. Potpuno analogno se pokazuje da F pripada K' te Sfere K i K' imaju zajednicki presijek cime je dokazan i treci slucaj. Pozdrav. [ zzzz @ 16.02.2009. 18:09 ] @
Mislim da nije dovoljno dokazati da kugle imaju zajedničku tačku pa
tvrditi da im se sfere sigurno sijeku. 1) Kugla sa centrom u tački M (koja proizvoljno leži u ravni plohe tetraedra ABC),radijusa MD,sadrži u sebi težište T. 2)Onda tačka T pripada i kugli sa centrom u N (ravan ACD) radijusa NB. 3)Sfere ovih kugli u svim slučajevima obuhvataju zajedničku tačku T i sjeći će se ako veća sfera ne obuhvata cijelu manju sferu. 4)Najmanja moguća sfera obuhvata cijeli tetraedar zbog NB>ND pa je sfera radijusa MD ne može obuhvatiti (jer je D unutar manje kugle). Fali još ovo: 5)Kako dokazati da kugla sa centrom u N,radijusa NB, ako ne sadrži tačku D ne može biti obuhvaćena većom sferom? (Zato sam ja išao na koncentrične kugle sa centrima u T i mislim da je sve ok dokazano.)  [ bata kg @ 19.02.2009. 22:34 ] @
Moram opet da spomenem "trougao i sestar".
Kada sam poceo da resavam ovaj problem tu je bilo svega i svacega: vektora, kruznica, lopti, projekcija i pitaj boga cega jos. Trebalo je dosta vremena da dodjem do sustine( makar za mene). Resio sam ga(jos jedno nadanje) onda kada je moje resenje bilo jasno i onima kojima "puca prsluk" za matematiku. Svako od nas "cepa" neku svoju teoriju, ali da li vidimo "sumu od drveca oko nas" Za moj ukus suvise teorije, znanja i obrazaca. Zamislit da je umesto E=mc^2 neka druga....niko je od nas smrtnika nebi znao. Vidim da smo dosta "icepali" ovaj zadatak, ima li neko predlog na sta sledece da se bacimo? [ zzzz @ 20.02.2009. 00:42 ] @
bata kg kaže:
najmanje duzine BN i DM su jednake visinama tacaka B i D. Bilo koja tacka van njih rezultuje vecim duzima. Spustimo tacke B i D u tacku preseka njihovih visina. Ova tacka ( na podjednakom rastojanju u odnosu na tacke B i D) i tacke N i M bilo gde cine trougao. Trougao egzistira i povecanjem dveju njegovih stranica za isti iznos( smanjene spustanjem). hvala na razumevanju i iscrpnom odgovoru ---- Ovdje si kiksao sa ovim "isti ..." pa si kasnije napravio neuspješnu doradu: ....Slika 6.Prikaz razlika sa slike 5.Prava B daje isti odsecak sa levom stranom a prava a deli razliku na iste vrednosti. Slika 7.Duz NX se skracuje i postaje NS,a MX se uvecava i postaje MS(tacka s se dobija presekom lukova).Skracenje i uvecavanje na osnovu slike 6.Tacka S sa MN(bilo gde da su) cine trougao. Povecanjem duzi NS i MS za isti iznos dobijamo duzi ND i MB nepromenjene u odnosu na sliku 1.Trougao i dalje egzistira. Primjeti ovo:Na onoj slici si spojio podnožja visina (nazovimo ih P1 i P2) i smatraš da je NP1+P2M=NM.A pravo NM je manje.Nevalja posao! Ovim nisi dokazao da ND-MB nije veće od MN.Sjedi 1, pa kad riješiš ispravno popravićemo ocjenu! [ zzzz @ 20.02.2009. 14:21 ] @
Izgleda mi da je glavni problem dokazati da razmak između tačaka M i N ne može
biti "prekratak".Razlika dužina ostale dvije stranice ne smije biti veća od tog razmaka, jer trougao nebi mogli konstruisati.Neki ovo u svojim dokazima potpuno zanemaruju. Ponoviću svoj dokaz malo jasnije i nadam se razumljivije. -Zadavanjem tačaka M i N možemo shvatiti i kao zadavanje dužina MD i NB. -Tražimo najnepovoljnije položaje za date dužine. --------------------- -M mora biti u ravni ABC i to na kružnici dobijenoj presjekom te ravni i plohe kugle sa centrom u D,radijusa MD. -Istu kružnicu dobijemo i presjekom te ravni sa koglom kojoj je centar u težištu tetraedra, a radijus jednnak udaljenosti MT. -Tačka M sigurno pripada plohi i te nove kugle. --------------------- -Isto uradimo i za tačku N.Dobijemo dvije koncentrične kugle koje sadrže zadane tačke. -Zaključujemo da, ma kako god pomjerali tačke M i N nemožemo ih približiti na manji razmak od razlike radijusa tih kugli (MT-NT).(Ne mogu se nalaziti van ploha svojih kugli.) -Dokažemo li još da je razlika stranica (MD-NB) manja od ove najkraće udaljenosti trougao se može sklopiti. (evo ponovo i nešto jasnije slike:) 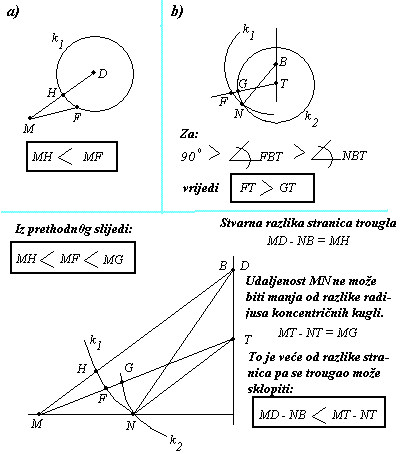 [ bata kg @ 25.02.2009. 17:36 ] @
Nisam mogao da se ranije javim na "popravni", riknulo mi napajanje i memorija, visa sila.
. . ..............Moja ideja za resenje je bila da fiksne tacke D i B objedinim u tacku preseka visina, i tako zaobidjem bilo kakvo dokazivanje bilo cega. To mi je omogucio sam prostorni oblik tetraedra i datih ravni. .............Jeste da sam prvo rekao da se uvecavaju za isti iznos, jer sam mislio da to i nije toliko bitno u odnosu na samu ideju resenja. To je Bojan odmah kritikovao. Na to sam dodao jednu prostu konstrukciju tako da sam tim resio i taj problem nejednakog produzenja. ..............Po meni.....spustiti tacke B i D u tacku preseka visina(mozda malo levo desno pomerenu- po meni nebitno, jer to sigurno moze) i ma gde bile M i N imamo trougao. Vracanjem iz zajednicke tacke u B i D trougao i dalje egzistira. Bitno je da uvecanja dovedu tacno krajeve duzi u pocetnu poziciju tacaka B i D. ............. Za ovo resenje i nije bitna pozicija Tacke M, N a kamoli rastojanje MN. . . .............. Najlepse kod ovog resenja je da ne postoje mesta napada. Naci zajednicku tacku..................................................................................moze Uvecati duzi za onoliko koliko treba da se vrate u pocetne pozicije.......................moze Trougao postoji i kad mu se dve strane podjednako povecaju..............................moze . . . . . istina je samo jedna, i to na mojoj strani! [ zzzz @ 26.02.2009. 12:40 ] @
...Trougao postoji i kad mu se dve strane podjednako povecaju..............................moze.
Za tetraedar stranice a=5 neka je MD=27 , NB=15 i MN=11.Probaj nacrtati ovaj trokut.Imaš pravo čak i podjednako povećavati stranice MD i NB ako će ti to šta pomoći. -Ako uspiješ onda si u pravu! -Ako ne uspiješ, a primjetiš da nije moguće da MN bude tako mala, opet si u pravu.Ali daj onda objasni kako znaš da duž MN ne može biti tako mala. [ bata kg @ 26.02.2009. 22:21 ] @
Duzi 15-27-11......u pravu si, ali nema potrebe za tim...
. . Ako imamo dve tacke bilo gde( M i N) i trecu "privremeno zajednicku" to je dovoljan i potreban uslov za jedan trougao. Zasto bih se upustao u preispitivanje razlicitih pozicija M i N kad one mogu biti "bilo gde". To je na kraju krajeva jedan od postulata geometrije. . . . U svom resenju kazes...trazimo najnepovoljniji polozaj......sta ako neko nadje jos nepovoljniji polozaj( ako ga ima) morao bi ponovo da nesta dokazujes. Odnos duzi je sigurno nezaobilazan faktor u jednom trouglu, ali je pojam tri tacke hijerajhijski iznad.....i sto je najvaznije sam sebi dovoljan. . Probao sam i ja sa loptama ciji su centri u B i D ali nism uspeo da sagledam dovoljno jasno kako to sve ide. Jednostavno sam se izgubio u silnim mogucim polozajima tacaka N i M. Probao sam i da izbacim date ravni kao uslov, ali nije moglo. U stvari nema opsteg resenja, postoje samo fragmentarna( do 90^o vazi, za veci ugao izmedju ravni zavisi od pozicije) . .Tvoj crtez prikazuje sve, trougao BD-M-N je tu, a tacno je i da je MD-NB<MT-NT. . . . .istina je samo jedna, i to na mojoj strani! [ zzzz @ 27.02.2009. 14:21 ] @
Ako imamo dve tacke bilo gde( M i N) i trecu "privremeno zajednicku" to je dovoljan i potreban uslov za jedan trougao.
Zasto bih se upustao u preispitivanje razlicitih pozicija M i N kad one mogu biti "bilo gde". To je na kraju krajeva jedan od postulata geometrije. Ako si siguran da je taj postulat dobar, smije li se koristiti još ponegdje? Evo primjera: Imamo pravilnu trouglu prizmu, baze su istostranični trouglovi, a visina 15x duža od ivice baze.Odaberimo tačku M na jednoj od bočnih ploha prizme, a N na drugoj bočnoj plohi. Označimo dvije ugaone tačke na suprotnim bazama prizme A i D. Napraviti trougao od duži MN, MA i ND, "ne upustajući se u preispitivanje razlicitih pozicija M i N kad one mogu biti "bilo gde".Samo izaberemo trecu "privremeno zajednicku" to je dovoljan i potreban uslov za jedan trougao." Čestitam! [ bata kg @ 28.02.2009. 22:25 ] @
Ovde je doslo do mnogo nesporazuma.
Koliko sam gledao tvoje resenje, ono je isto kao i moje. I ti mislis da iz zajednicke tacke T mozemo u tacku B D bez promene zadatih duzina u odnosu na tacke M i N. To je kljucno za mene. E, ovde ti nastavljas dalje sa analizom odnosa stranica, sto po meni nema potrebe. Ti si prosto presao preko resenja da bi analizirao stranice. . . . .istina je samo jedna, i to na mojoj strani (nesta gledam ovu izreku pa se izvinjavam ako deluje mozda napadno, ona potice iz vremena kad sam igrao GO pa mi je tako i ostala) [ Bojan Basic @ 07.03.2009. 22:11 ] @
Evo konačno i mene, uz još jedno izvinjenje zbog kašnjenja s komentarima.
Zzzz, tvoje rešenje je u redu. Po dužini ipak malo premašuje ovo „apstraktno“ rešenje koje ja imam (a koje ću, naravno, napisati kad završimo diskusiju o svim ovde iznetim idejama), ali svejedno mogu samo da ti čestitam. Što se mene tiče, nisi ni morao da se trudiš oko izbacivanja analize (ja sam žestok protivnik bilo kakvog ograničavanja oko aparature koja se sme koristiti prilikom rešavanja nekog problema), ali to je svakako samo upotpunilo sliku. Citat: bata kg: Slika 6.Prikaz razlika sa slike 5.Prava B daje isti odsecak sa levom stranom a prava a deli razliku na iste vrednosti. Slika 7.Duz NX se skracuje i postaje NS,a MX se uvecava i postaje MS(tacka s se dobija presekom lukova).Skracenje i uvecavanje na osnovu slike 6.Tacka S sa MN(bilo gde da su) cine trougao.Povecanjem duzi NS i MS za isti iznos dobijamo duzi ND i MB nepromenjene u odnosu na sliku 1.Trougao i dalje egzistira. Prvih pet slika sam razumeo, ali nikako ne kapiram šta prikazuješ na ovoj šestoj. Da li možeš taj deo objasniti još malo? Pročitao sam i šta ste posle pričali ti i zzzz, ali nisam ni tamo našao razjašnjenje. Citat: galet@world: Evo i mog pokušaja Ovde mi neke stvari nisu baš najjasnije. Kako pod tačkom 1 (a na isto se pozivaš i kasnije) zaključuješ da je 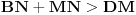 (objašnjenje koje daješ je „jer put od tačke (objašnjenje koje daješ je „jer put od tačke  do tačke do tačke  preko tačke preko tačke  prolazi kroz ravan prolazi kroz ravan 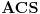 dva puta“, ali ne vidim zašto je to dovoljno)? Druga nejasnoća je na samom kraju tvog dokaza, kada primećuješ da će tačka dva puta“, ali ne vidim zašto je to dovoljno)? Druga nejasnoća je na samom kraju tvog dokaza, kada primećuješ da će tačka 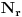 pasti s druge strane ravni pasti s druge strane ravni 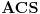 , za šta mi se čini da nemaš dovoljno argumenata. Verujem da to izvlačiš iz činjenice da je stranica , za šta mi se čini da nemaš dovoljno argumenata. Verujem da to izvlačiš iz činjenice da je stranica 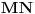 najduža u trouglu najduža u trouglu 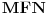 , ali možda još jedna rečenica koja to sasvim razjašnjava nije na odmet. , ali možda još jedna rečenica koja to sasvim razjašnjava nije na odmet.Malada, u vezi s tvojim rešenjem mogu samo da se složim s primedbom koju je dao zzzz. [ galet@world @ 08.03.2009. 21:10 ] @
Citat: Bojan Basic:Ovde mi neke stvari nisu baš najjasnije. Kako pod tačkom 1 (a na isto se pozivaš i kasnije) zaključuješ da je 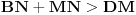 (objašnjenje koje daješ je „jer put od tačke (objašnjenje koje daješ je „jer put od tačke  do tačke do tačke  preko tačke preko tačke  prolazi kroz ravan prolazi kroz ravan 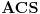 dva puta“, ali ne vidim zašto je to dovoljno)? dva puta“, ali ne vidim zašto je to dovoljno)?Ja mislim da jeste - evo pogledaj u prilogu. Citat: U pravu si - nekad hoće, a nekad neće - evo i dokaza kad neće. [ galet@world @ 10.03.2009. 18:10 ] @
U prilogu dostavljam jednostavno i kompletno rešenje. Bojane interesuje me tvoj komentar jer mislim
da sam ovaj put razumeo zadatak i, čini mi se, da sam dao vrlo jednostavno rešenje. Ovo rešenje je prikaz već datog rešenja i ne ponavlja dokazivanje, ali mislim da je jasnije prikazano. [ holononi @ 29.05.2009. 22:02 ] @
Citat: Neka je pravilan tetraedar i , različite tačke u ravnima i , redom. Pokazati da su duži , i stranice nekog trougla. (1) Neka je M=B i N=C, važi M je u ravni ABC i N je u ravni ADC. Tada se duž BN poklapa sa duži MN a duž MD se poklapa sa duži BD. Tada su MN, BN i MD stranice trougla BCD. Medjutim, (2) Neka je M tačka u težištu trogla ABC a tačka N u težištu trougla ADC (mogu se uzeti i druge tačke, ovo je samo da se lakše komunicira). Tada su duži MN, BN i MD duži otvorene poligonalne linije pa ne obrazuju trougao. I ne samo to, te četiri tačke ne mogu biti na stranicam jednog trougla, ma kako ga kostruisali. Ravan u kojoj se nalaze tačke B, M i N je različita od ravni u kojoj se nalazi tačka D. Zato te tri duži ne mogu pripadati jednom trouglu. Do istog zaključka se dolazi posmatranjem pravih koje prolaze kroz ove tačke. Sa tri prave koje ne leže u istoj ravni ne može se konstruisati traženi trougao. Medjutim, (3) Ako se ono pod (2) posmatra duž prave definisane tačkama D i M, tada se duž MD projektuje u tačku M pa je dobijen traženi trougao i to MNB. Prema tome, svi su u pravu. [ galet@world @ 30.05.2009. 18:43 ] @
Mislim da ono pod 2 nije tačno kad se radi o težištima trouglova. Sve četiri tačke su u tom slučaju u jednoj ravni,
a ako su te tačke bilo gde (a ne u težištima) onda ne moraju biti u jednoj ravni, ali koliko sam ja razumeo zadatak to i ne mora da bude - važno je da se od te tri duži može konstruisati trougao, odnosno, kad se tri duži koje ne leže u istoj ravni "smeste" u jednu ravan onda se od njh može konstruisati trougao. [ holononi @ 31.05.2009. 00:01 ] @
Citat: važno je da se od te tri duži može konstruisati trougao Ako je to suština zadatka, onda je diskusija po tom pitanju završena. [ galet@world @ 31.05.2009. 06:19 ] @
Citat: holononi: .... onda je diskusija po tom pitanju završena. Možda jeste, možda nije Jer još Bojan tajnu krije! Citat: Bojan Basic:Rešenje koje ja imam ne koristi vektore. Zapravo, imam dva rešenja, od koje je jedno ono „apstraktno“ iz naslova, dok je drugo prizemnije(i dosadnije); nebitno, nijedno od njih ne koriste vektore. No, to svakako ne znači da je nemoguće rešiti zadatak preko vektora — probaj, pa ako uspeš, super. Citat: Bojan Basic:Zzzz, tvoje rešenje je u redu. Po dužini ipak malo premašuje ovo „apstraktno“ rešenje koje ja imam (a koje ću, naravno, napisati kad završimo diskusiju o svim ovde iznetim idejama), ali svejedno mogu samo da ti čestitam. Ovde je ravno pa može da se piše. [Ovu poruku je menjao galet@world dana 31.05.2009. u 07:30 GMT+1] [ holononi @ 31.05.2009. 09:40 ] @
Ako se posmatra pravilan tetraedar tako da se osnovica BCD nalazi dalje a teme A bliže posmatrača, tada izabrati tačke M i N na sledeći način. Tačka M neka je na ivici BC pa je u ravni ABC. Slično, tačka N neka je na ivici CD i zadovoljava uslov da je u ravni ADC. To je otvorena poligonalna linija i kao takva nije trougao iako su sve četiri tačke u istoj ravni BCD. Ako se posmatra tačka A' projekcija tačke A na težište trougla BCD, uočava se trougao MNA' pa je dobijen neki trougao.
Ako se tačka N pomeri van prave date tačkama C i D i to tako da ostane u ravni ADC, tada je tačka N van ravni BCD u kojoj se nalaze ostale tri tačke. Kako te četri tačke mogu biti delovi jednog trougla? Naravno od tih stranica je moguće konstruisati neki trougao, no tada su potrebne dodatne operacije, što se u zadatku ne pominje ali se ni ne zabranjuje@ Reklo bi se da zadatak zahteva malo dorade ili komentar iz kog je konteksta izvadjen. 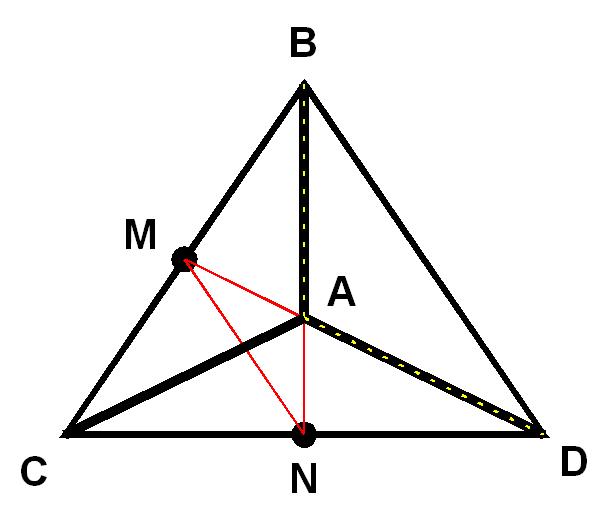 [ galet@world @ 31.05.2009. 19:00 ] @
Citat: holononi: Reklo bi se da zadatak zahteva malo dorade ili komentar iz kog je konteksta izvadjen. Sve je "dorađeno". Ako se prati tema od početka mora se naići i na ovo: Citat: Bojan Basic: Ne. Tačke i određuju pomenute duži, i na te tačke ne možeš uticati — takve su kakve su. E sad, kad dobiješ duži, onda ih možeš „iščupati“ iz tetraedra i negde sa strane od njih formirati trougao. Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|