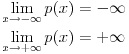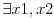[ friky @ 07.04.2005. 19:45 ] @
| Dobio sam ovo kao esej, nazalost, ne znam bas ovo rijesavat, molio bih dobru dusu ako netko ima volje da pomogne: 1) Pokazite da jednadzba x³ + 2x² - x + 1 = 0 ima barem jedan realan korijen. 2) Upotrebem teorema o medjuvrijednosti pokazite da je kubna jednadzba x³ + ax² + bx + c = 0 ima barem jedan realan korijen. Puno hvala |