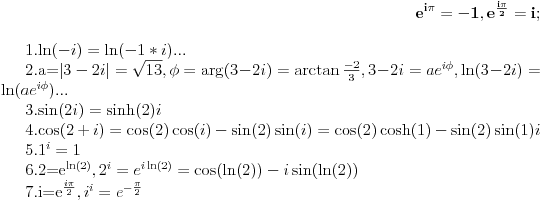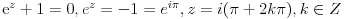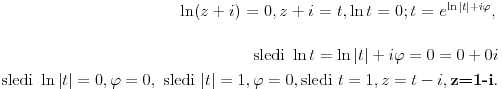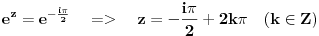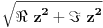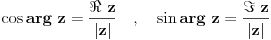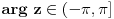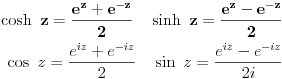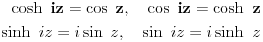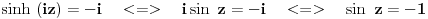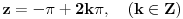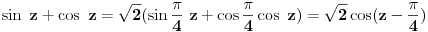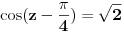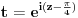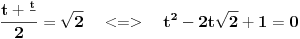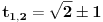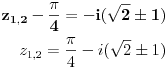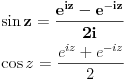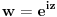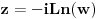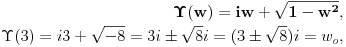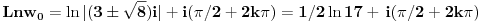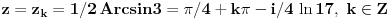[ dalibor_ratkaj @ 12.04.2005. 12:51 ] @
| Moram napisat esej na temu "kompleksne funkcije kompleksne varijable" pa bih molio za neki link gdje mogu naci materijale o tome... Imam i par zadataka za rijesiti...pa ako netko zna... ln(-i) ln(3-2i) sin2i cos(2+i) arccosi 1 na i 2 na i i na i Hvala!! |