Ništa. Znači da drugi izvod nema nulu, tako da ni funkcija nema prevojnu tačku.

Ne bass,

Tacka u kojoj je funkcija definisana mozze biti prevojna iako u njoj ne postoje izvodi. Prevojna tacka razdvaja skupove tacaka u kojima je funkcija konveksna odnosno konkavna

[att_img]

Daklem prvi izvod govori o tangentama (u tački) ili o monotonosti (na intervalu). Ukoliko prvi izvod u tački x=x₀ postoji & konačan je jednačina tangente u tački M(x₀, f(x₀)) (koja pripada grafiku f-je y=f(x)) glasi



Ukoliko izvod postoji, ali nije konačan tangenta ima oblik x=x₀

Najzad ukoliko f-ja nema izvod u tački, ona nema ni tangentu (bar ne jedinstvenu)

Toliko o vrednosti izvoda f-je u tački.

Ukoliko f raste na [a,b]
Ukoliko f opada na [a,b]

Ukoliko f je konvexna na [a,b]
Ukoliko f je konkavna(ili konvexna na dole) na [a,b]


Kao što vidiš, nema razloga da ispituješ vrednost drugog izvoda u ma kojoj tački.

Monotonost (raste/opada) i konvexnost f-je nisu pojmovi vezani za tačke, već za intervale.
Jedino što nas zanima vezano za tačke su
granice intervala monotonosti (lokalni extremumi)
i granice intervala konvexnosti (tačke prevoja)

Dakle izvod u tački NE MORA da bude nula da bi funkcija tu imala min/max vrednost.
Čak i ako izvod jeste 0 to NE MORA biti min/max vrednost.

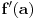
Polako, prvo treba znati definicije. Izvod je po definiciji

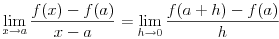
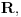
ako postoji. Pritom se taj limes posmatra u tako da po definiciji mora biti konačan. Sa druge strane, može se govoriti i o tome da je izvod u nekoj tački beskonačan, ali se tada o izvodu govori u uopštenom, a ne u osnovnom smislu. Prevojna tačka je tačka u čijoj je nekoj okolini (koja naravno uključuje i tu tačku) funkcija diferencijabilna, a u kojoj se monotonost ozvoda funkcije menja. Recimo, funkcija

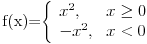
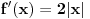
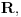
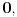
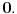
ima izvod na celom skupu ali u tački nema drugi izvod (van te tačke drugi izvod postoji i jednak je nuli). Međutim, prvi izvod postoji u tački , kao i u nekoj okolini te tačke (štaviše, na celom skupu realnih brojeva), pri čemu on opada u delu te okoline levo od tačke a raste u delu okoline desno od tačke Drugim rečima, ta tačka je lokalni minimum prvog izvoda funkcije, pa jeste prevojna. Prevoji su ništa drugo do lokalni ekstremi izvoda funkcije.

Ako funkcija ima prevoj u nekoj tački, onda ona ne mora da bude dva puta diferencijabilna u njoj, ali ako drugi izvod u toj tački postoji, onda on mora biti jednak nuli.

Ha, Nedjo, uhvatio sam te. Ako drugi izvod postoji u tački prevoja, on je 0 ili

npr treći koren od x (ne znam što TEX sad zeki)
Ali stvarno mi je dosta ljudi koji objasne da ćemo max/min naći u tački gde je izvod 0. To kaže neki usporeni predavač, čuju đaci i ...

DECO!
Ne verujte čika profesoru ako kaže da ćete naći max/min u tačkama gde je prvi izvod 0.

TO NIJE TAČNO.

Ako prvi izvod postoji u tački max/min i konačan je, onda je prvi izvod jednak 0. TO JESTE TAČNO.

Ne mešajte uzrok & posledicu.

Ako je prvi izvod u tački 0, onda je to kritična tačka. U njoj može biti max/min(x²) ili prevoj (x³)

Ako je prvi izvod u tački beskonačan, opet tu može biti max/min (x^2/3) ili prevoj(x^1/3).

Ako je tačka na rubu Domena f-je, to je sigurno max/min ()