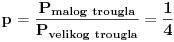Od duži x, y, z se može formirati trougao akko je x<y+z, y<x+z, z<x+y. Naš početni uslov kaže da je x+y+z=L.

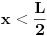
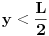
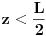
Dakle x<L-x tj . Isto i . Umesto z ubacimo L-x-y, i dobijamo

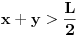
Eh, sad što se tiče slučajnog odabira tri duži...Znamo da x, y>0 i da L-x-y>0, tj x, y>0, x+y < L. Prtepostavićemo da slučajno biramo x i y, tako da x, y>0 i da L-x-y>0, i da je promenljiva (x,y) uniformne raspodele nad dozvoljenim skupom. Za ne-matematičare da tačka može biti bilo gde u velikom trouglu : x, y>0 L-x-y>0, i to sa podjednakim verovatnoćama (Nedeljko će me, verovatno pojesti, ako pročita ovu rogobatnu konstrukciju rečenice)
[img][att_url][/img]
Da bismo mogli da dobijemo 3-ugao tačka mora biti u malom trouglu.

Verovatnoća da budu izabrane takve duži da bude moguća konstrukcija 3-ugla je

Hvala puno na preciznom i slikovitom objasnjenju.