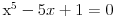E "Srki" a znas onu formulicu
[Q(a):Q]<>2^m=>a nije konstruktabilan
???????????????????????????????????????

Trisekcija ugla je resena. Patentirana je u Zavodu za intelektualnu svojinu, a problem je resila profesorka matematike u penziji iz Zarkova - Beograd. Inace, majka mog druga. Gospodja se preziva Slavic.

Iskopao si temu 3 godine staru, a inace mnogo duza tema na ovu raspravu se nalazi ovde:
http://www.elitesecurity.org/tema/11190

tako da ova tema moze da se brise.
Dokaz da trisekcija ugla nije moguca se nalazi ovde:
http://www.cut-the-knot.com/arithmetic/cubic.shtml

a takodje smo raspravljali i o toj patentiranoj "trisekciji" od te nase profesorke. To sto je nesto patentirano ne znaci da radi. Imas mali milion patenata koji pokusavaju da dobiju energiju ni iz cega ali to ne znaci da to radi. Trisekcija ugla je odavno bila moguca ali ako se recimo lenjir koristi na nestandardan nacin ili ako podelimo odredjen postupak u vise iteracija cime u svakom krugu smanjujemo gresku pa mozemo doci do proizvoljne tacnosti.

Seccam se da je moj profesor geometrije na PMF D.Lopandic na jednom od predavanja rekao da zna oko 40 "ressenja" trisekcije ugla - naravno sve sa ponekim
logicckim felerom. Problem kod amatera matematiccara je da uz to ssto imaju dosta ideja uvek naprave poneki previd za koji nisu ni svesni.

Što se tiče nepostojanja formule za rešavanje algebarske jednačine petog i višeg stepena, pošto svaka algebarska jednačina stepena bar jedan ima rešenja u polju kompleksnih brojeva, treba znati preciznu formulaciju tog problema.

Naime, za rešenje algebarske jednačine izraženo konačnim izrazom u kome učestvuju koeficijenti jednačine kao konstante, zatim operacije sabiranja oduzimanja, množenja i delenja i korenovanja proizvoljnog stepena (pri čemu rezultat uvek može biti željeni n-ti koren iz potkorene veličine jer n-tih korena iz kompleksne konstante različite od nule ima n) se kaže da je izraženo preko radikala. Rešiti algebarsku jednačinu preko radikala znači izraziti sva njena rešenja preko radikala. Dokazuje se da nijedno rešenje jednačine

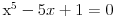
nije izrazivo preko radikala. Dokaz je izuzetno složen i izlaže se u okviru Galoaove (Galois) teorije. Takve se stvari mogu naći u bilo kojoj dobroj knjizi koja obrađuje tu teoriju. Potraži knjige iz algebre u kojoj se izlaže teorija algebarskih polja (i njihovih raširenja). Takve stvari su inače standardni deo kurseva algebre za studente matematike.