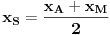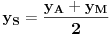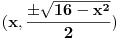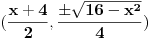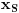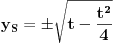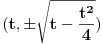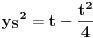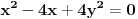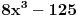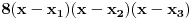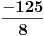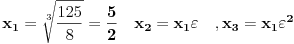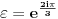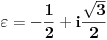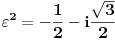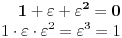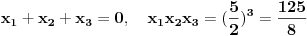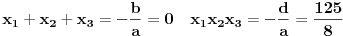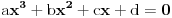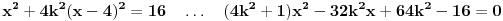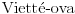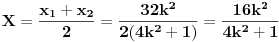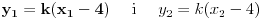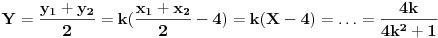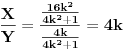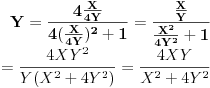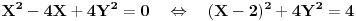Što se prvog zadatka tiče, ako te zanima izračunavanje izraza bez Viette-ovih formula, lepo izračunaj x
1, x
2, x
3 & mirna Bačka.
Mala naznaka: računanje rešenja, u opštem slučaju, ni najmanje nije lepo ni lako; no u ovom zadatku to jeste lepo & lako.
Lepo & lako za svakog ko je dobar prijatelj sa kompleksnim brojevima, to jest.
Dakle
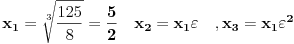
gde je
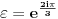
tj
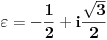
.
Takođe tada je
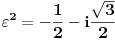
Kao što znamo
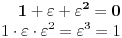
Dakle
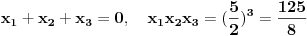
.
Napominjem, ovo je bilo lepo & lako. Viette daje nešto brže ...
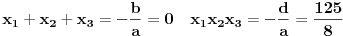
Ovde se podrazumeva da imamo j-nu
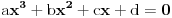
Drugi zadatak je baš leeep.
No, sad vidim da ga je lampica uradila tačno, mada za nijansu zakomplikovano.
Code:
@ lampica
Nisi trebala da stavljaš x=t, jer to stvarno neme nikakve veze ni sa čim.
Ovako si uradila na jako dobar način, primećujući da je A na početnoj elipsi,
a da M može biti bilo koja druga tačka na elipsi.
Ako neko ne vidi sve ovo, taj mora da (što se kaže) seče drva sekirom (tj da učestvuje u dugom & dosadnom poslu računa bez ikakvog učestvovanja mozga)
Daklem, evo cepanja drva
Pretpostavimo da je t:y=k(x-4) jednačina tetive.(bez obzira na k, ova prava sigurno prolazi kroz A) Ubacimo to u jednačinu elipse, da bismo dobili x
1, 2.
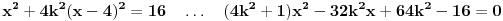
Primenimo
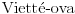
pravila da izračunamo
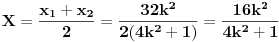
Pošto je
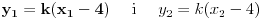
, vidimo da je i
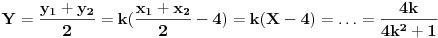
Eh, sad treba izbaciti to k.
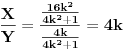
Zamenimo sve to npr u Y.
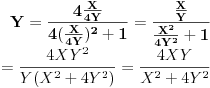
Dakle

, tj
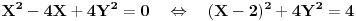
Dakle rešenje:
Centri datih tetiva pripadaju elipsi, kojoj je centar C(2, 0), a poluose su a=2, b=1. Ova elipsa prolazi kroz centar početne elipse, kao i kroz A. Štaviše, to su joj temena.