1. zadatak

Resiti u skupu realnih brojeva R jednacinu:


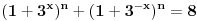
(n je verovatno celi broj)

Resenje:
Treba uociti da su jedine mogucnosti n=1 ili n=2 (za n>2 jedan od sabiraka je sigurno veci od 8).

Zamenom ovih vrednosti za n lako se dobijaju sva resenja.

2. zadatak

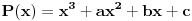
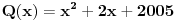
Polinom ima 3 razlicite realne nule, dok polinom P(Q(x)) nema realnih nula gde je . Dokazati da je P(2005) > 1.

Resenje:
Neka su x1, x2 i x3 realne nule polinoma P(x). Tada vazi:
P(x) = (x - x1)(x - x2)(x - x3).
P(Q(x)) = (Q(x) - x1)(Q(x) - x2)(Q(x) - x3)

Realne nule polinoma P(Q(x)) su sve nule polinoma Q(x) - xi, i = 1, 2, 3. Kako P(Q(x)) nema realnih nule, nijedan od ova tri polinoma ih takodje nema (ovo je ekvivalencija).

To znaci da polinomi

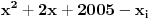
nemaju realnih nula. Ili drugim recima (gledamo znak determinante):
.

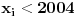
Sada dobijamo:
P(2005) = (2005 - x1)(2005 - x2)(2005 - x3)

Svi cinioci su veci od jedinice, iz cega zakljucujemo da je P(2005) > 1.

[img][att_url][/img]



[img][att_url][/img]