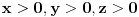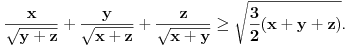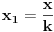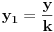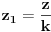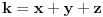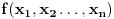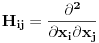[ Metalnem @ 02.05.2005. 15:50 ] @
|
[ Bojan Basic @ 05.05.2005. 13:54 ] @
[ Metalnem @ 05.05.2005. 15:24 ] @
To je to, hvala!
[ Metalnem @ 07.05.2005. 21:02 ] @
Sada me interesuje jos nesto. Recimo da imamo neku funkciju vise promenljivih, konkretno
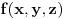 . Da li je tacno sledece: . Da li je tacno sledece:Funkcija 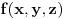 je konveksna ako vazi: je konveksna ako vazi: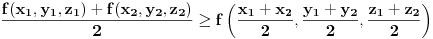 . .Za konveksnu funkciju 3 promenljive vazi: 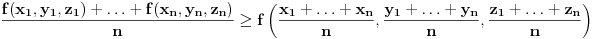 . .Ako je tacno, da li se konveksnost ovakve funkcije moze dokazati preko izvoda, kao sto moze za funkciju jedne promenljive? [ Bojan Basic @ 07.05.2005. 22:58 ] @
Prema definiciji funkcija
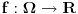 gde je gde je 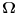 neki vektorski prostor (ako ne znaš šta je vektorski prostor samo zamisli to kao funkciju više promenjivih, to je to u suštini) je konveksna ako za svako neki vektorski prostor (ako ne znaš šta je vektorski prostor samo zamisli to kao funkciju više promenjivih, to je to u suštini) je konveksna ako za svako 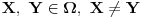 i za svako i za svako 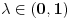 važi važi 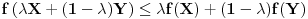 . .Provera preko izvoda je moguća ali je nešto složenija nego kod funkcija jedne promenljive. Neka je funkcija 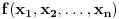 dva puta diferencijabilna. Posmatrajmo sledeću matricu: dva puta diferencijabilna. Posmatrajmo sledeću matricu: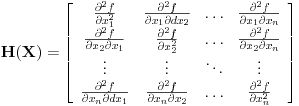 Funkcija je konveksna na nekom intervalu  akko je akko je 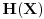 pozitivno definitna (positive definite) za sve pozitivno definitna (positive definite) za sve 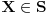 . .Kao što vidiš situacija se prilično komplikuje uvođenjem više promeljivih, ali dobra ideja nekad ume jako da pojednostavi stvari. Primera radi, dokazati da je funkcija 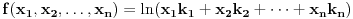 za neke fiksne za neke fiksne 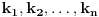 konkavna (nije teško ali ovakva ideja ume da bude od koristi pa sam zato napisao ovaj primer). konkavna (nije teško ali ovakva ideja ume da bude od koristi pa sam zato napisao ovaj primer).[Ovu poruku je menjao Bojan Basic dana 06.10.2007. u 22:30 GMT+1] [ Sinalco @ 08.05.2005. 18:52 ] @
Ma to ti je izvod drugog reda... Nisam bas siguran da li je to potreban i dovoljan uslov konveksnosti :-)
[ Bojan Basic @ 08.05.2005. 19:23 ] @
Čekaj bre, Aco, jesi li siguran da to ne valja? Ja sam oduvek tako radio i bilo je OK.
P. S. Evo sad nađoh i neke reference o tome na netu, pogledaj http://www.economics.utoronto.ca/osborne/MathTutorial/CVNF.HTM. [Ovu poruku je menjao Bojan Basic dana 19.05.2008. u 00:49 GMT+1] [ Metalnem @ 17.05.2005. 20:59 ] @
[ Sonec @ 21.10.2011. 01:14 ] @
[ Nedeljko @ 19.05.2023. 10:17 ] @
Ne znam zašto se nigde ne pominje svođenje dokazivanja konveksnosti funkcija više promenljivih na slučaj jedne promenljive, pa hajde ja da napišem.
Neka je funkcija  definisana na konveksnom domenu. Tada je funkcija definisana na konveksnom domenu. Tada je funkcija  (strogo) konveksna (odnosno konkavna) akko je za ma koje različite tačke (strogo) konveksna (odnosno konkavna) akko je za ma koje različite tačke 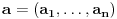 i i 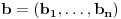 funkcija funkcija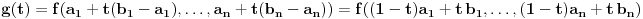 za za 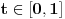 . .Tada se u slučaju diferencijabilnosti, odnosno dvostruke diferencijabilnosti može koristiti kriterijum za funkcije jedne promenljive, s tim da se to mora dokazati za sve međusobno različite  i i  iz domena. Ukoliko je funkcija iz domena. Ukoliko je funkcija  definisana preko neke funkcije jedne promenljive kao u navedenom zadatku, onda se lako rešava onako kako je Sonec napisao. definisana preko neke funkcije jedne promenljive kao u navedenom zadatku, onda se lako rešava onako kako je Sonec napisao.Za funkcije jedne promenljive važi da je funkcija 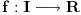 , gde je , gde je  pravi interval (ograničen ili neograničen) (strogo) konveksna akko je zadovoljen bilo koji od sledećih ekvivalentnih uslova: pravi interval (ograničen ili neograničen) (strogo) konveksna akko je zadovoljen bilo koji od sledećih ekvivalentnih uslova:1) Za ma koje 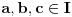 takve da je takve da je 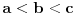 važi da je determinanta važi da je determinanta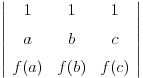 (strogo) veća od nule. Ovde "veća" bez "strogo" znači "veća ili jednaka". 2) Pod uslovom da je  najmanja vrednost intervala najmanja vrednost intervala  , funkcija , funkcija  je (strogo) konveksna na intervalu je (strogo) konveksna na intervalu 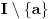 , važi da je , važi da je 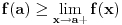 . .3) Pod uslovom je  najveća vrednost intervala najveća vrednost intervala  , funkcija , funkcija  je (strogo) konveksna na intervalu je (strogo) konveksna na intervalu 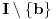 , važi da je , važi da je 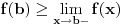 . .4) Ako za barem jedno 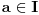 važi da je funkcija važi da je funkcija 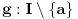 , , 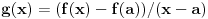 (strogo) monotono neopadajuća. Ovde "strogo monotono neopadajuća" znači "strogo rastuća". (strogo) monotono neopadajuća. Ovde "strogo monotono neopadajuća" znači "strogo rastuća".5) Ako za svako 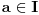 važi da je funkcija važi da je funkcija 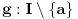 , , 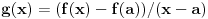 (strogo) monotono neopadajuća. (strogo) monotono neopadajuća.6) Pod uslovom da interval  nema najmanju niti najveću vrednost i da je funkcija nema najmanju niti najveću vrednost i da je funkcija  diferencijabilna na njemu, važi da je funkcija diferencijabilna na njemu, važi da je funkcija 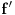 monotono neopadajuća, i da u slučaju da se traži stroga konveksnost važi da monotono neopadajuća, i da u slučaju da se traži stroga konveksnost važi da 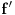 nije konstantno ni na jednom pravom intervalu. nije konstantno ni na jednom pravom intervalu.7) Pod uslovom da interval  nema najmanju niti najveću vrednost i da je funkcija nema najmanju niti najveću vrednost i da je funkcija  dva puta diferencijabilna na njemu, važi da je funkcija dva puta diferencijabilna na njemu, važi da je funkcija 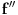 nenegativna, i da u slučaju da se traži stroga konveksnost važi da nenegativna, i da u slučaju da se traži stroga konveksnost važi da 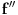 nije konstantno jednako nuli ni na jednom pravom intervalu. nije konstantno jednako nuli ni na jednom pravom intervalu.Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|