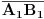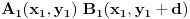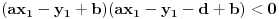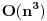'Ajde ponovi to što si rekao.

Molim te formuliši zadatak. Kakve su duži ? Seku li x-osu ? Koja su im međusobna rastojanja ? Kakva prava treba da bude ? Da li može da ih seče u krajevima ili ne ?

Ovo je ipak matematički forum.

Ako se radi o 2D problemu (xOy) tada svaka prava normalna n x-osu ima jednacinu
x=a
gde je a konstanta - broj na x-osi.
Duzz u ravni bi se mogla opisati parametarskim jednacinama

x=p
y=t q<t<r


gde je t promenljivi parametar a p,q i r neke konstant

[att_img]



Malo je pitanje nejasno.
Slicno bi bilu u 3D.

Kakve su duži ? Seku li x-osu ?
Duzi k'o duzi, ograničene. neke mozda sjeku x-osu, neke ne. Sve su okomite na x-osu (ugao 90 zaklapaju sa x-osom).

Koja su im međusobna rastojanja ?
Međusobna rastojanja - jednaka.
za npr. x=1, duz npr. od y1=3 do y2=4
za x=2, duz npr od y1= 3,5 do y2=4,5
za x=3, duz npr od opet y1= 3,5 do y2=4,5
...itd

i tako x raste za po jedan uvjek (X_n - X_n-1) = 1
kao i za duzi uvjek vazi y2-y1=const (odnosno u primjeru koji sam naveo y2-y1=1)

Kakva prava treba da bude ?
ne razumijem, obicna prava linija (y=ax+b)

Da li može da ih seče u krajevima ili ne ?
da, može da ih sječe u krajevima.

Ako imaš zadatu duž gde je , prava
p:y=ax+b
tj
p:ax-y+b=0 će je seći akko


Postavi svih n takvih nejednačina. Dobio si sistem kvad nejednačina. Bilo koji brojevi a i b koji zadovoljavaju dati sistem daju pravu koja seče sve duži. Kao što vidiš, rešenje uopšte ne mora da postoji.

Hvala velika na pomoći.
Eh sad samo ... kako da to implementiram u programu.
Malo je problematična ova implementacija sistema nejednačina programski.
Ili možda postoji neki elegantan način i za to?

Ajde malo da se prebacimo na Art Of Programming :).

Bio je slican ovakav zadatak pre 3-4 godine na saveznom iz programiranja... Mozes dokazati (sto vazi inace, ne samo ako su prave paralelne x osi) da prava koja sadrzi najvise njih moze da prolazi kroz dve krajnje tacke nekih duzi (vrlo je ocigledno, kad zamislis pravu koja sece maksimalan broj duzi, uvek mozes da je zarotiras za neki mnogo mali ugao tako da dodje do toga da neku od duzi koje sece sece bas u krajnoj tacki). Onda mozes lepo uzeti sve prave definisane krajevima duzi, pa za svaku od njih proveriti da li sece sve ostale duzi. Slozenost bi bila

Ovo ti je jedan od najvažnijih zadataka u veštačkoj inteligenciji : Naći što jednostavnije uslove pomoću kojih možeš podeliti skup pojedinih tačaka na nekoliko delova, ukoliko se zna koje tačke pripadaju kojem delu. Nađeno je mnogo algoritama, pokušalo se na mnogo načina...

Kao što rekoh ranije - U opštem slučaju ne postoji rešenje

Pokušaj ovako

U dvostrukom ciklusu postavljaj prave kroz donje tačke, sve dok ne nađeš pravu iznad koje nemaš donjih tačaka. (Takva prava mora da postoji). Zovimo je "donjom pravom"

Onda u dvostrukom ciklusu postavljaj prave kroz gornje tačke, sve dok ne nađeš pravu izpod koje nemaš gornjih tačaka. (I takva prava mora da postoji) Zovimo je "gornjom pravom"

Posmatraj gornju poluravan donje prave i donju poluravan gornje prave. Njihov presek ne mora da postoji. Ali, ako postoji, svaka poluprava koja mu pripada seče sve duži.

@KPYU:
Prava koju trazimo ne mora da bude paralelna sa x-osom, pa ovo nece da radi. Pa ne znam sta podrazumevas pod "resenjem", ali ako prihvatas za resenje agoritam polinomijalne slozenosti, procitaj moj prethodni post, videces da itekako ima resenja (u opstem slucaju)