[ nemanjaa @ 06.05.2005. 17:23 ] @
| najmanja vrednost funkcije f(x)=cosx + sinx _? ja sam pokusao preko ekstremnih vrednosti da odredim minimum. ali nece. evo vec sat vremena pokusavam ali nazalost bezuspesno..... |
|
[ nemanjaa @ 06.05.2005. 17:23 ] @
[ devetkamp @ 06.11.2011. 13:09 ] @
Meni nije jasno kako odrediti NAJVECU vrednost funkcije y = (sinx)^2 - 6sinx + 12. Moze se odrediti NAJMANJA vrednost preko kvadratne funkcije. I ona iznosi 3. A kako odrediti NAJVECU vrednost? I kako uopste nacrtati grafik ove funkcije? Praviti tablicu ili tako nesto?
[ Sonec @ 06.11.2011. 13:26 ] @
[ devetkamp @ 06.11.2011. 16:01 ] @
To je i tacno.Uvodio sam smenu sinx=t, pa dobio kvadratnu funkciju i iskoristio njen minimum. Ali sam posle shvatio da ne moze tako. I lepo nacrtam grafik preko tablice i vidim resenje. Mada to nije uvek pouzdano. Kako ti radis? Znam da moze preko integrala, ali njih jos nismo ucili. Koji je drugi nacin?
[ Sonec @ 06.11.2011. 16:08 ] @
A da li znas izvode? Pretpostavljam da ste skoro radili izvode, posto si 4 godina. Ako jeste, onda nadjes min i max preko prvog izvoda.
[ devetkamp @ 06.11.2011. 16:13 ] @
Nismo ni izvode radili. Jos smo kod limesa... :( . A moze li nekako drugacije?
[ Sherlock Holmes @ 06.11.2011. 16:26 ] @
[ Sonec @ 06.11.2011. 16:29 ] @
[ devetkamp @ 06.11.2011. 16:40 ] @
Dakle, funkcija dostize MAKSIMUM za x=3pi/2, a minimum za x=pi/2. Hvala puno... Nismo ovakvu vrstu zadataka uopste ni radili na casu. Sad spremam prijemni, pa moram sve to da predjem... :D
[ Sonec @ 06.11.2011. 16:46 ] @
Pa verovatno niste radili zasto sto niste radili izvode. Kada njih uradite, videces koliko je ovo lako.
[ devetkamp @ 06.11.2011. 16:51 ] @
Ok. Hvala puno...
[ darkosos @ 07.11.2011. 07:32 ] @
Samo da dodam, ovde ne mora da se radi sa izvodima, funkcija
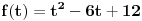 se radi u valjda drugom razredu srednje i kaze se da ima min u temenu, koje je ovde tacka (3,3), se radi u valjda drugom razredu srednje i kaze se da ima min u temenu, koje je ovde tacka (3,3),opada za x <= 3 i raste za x >= 3. Posto sin(x) uzima vrednosti u [-1,1], znaca da trazimo min i max f(t) na intervalu [-1,1]. Posto je f(t) opadajuca na ovom intervalu, max f = f(-1) = 19 a min f = f(1) = 7. [ devetkamp @ 07.11.2011. 12:39 ] @
Znaci postoje 3-4 nacina kako se ovo radi... Zahvaljujem jos jednom...
[ Sherlock Holmes @ 07.11.2011. 13:58 ] @
Da, vec sam ti napisao.
Citat: Sherlock Holmes: 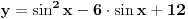 Postavis dve ose: 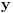 i i 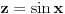 . Nacrtas grafik kvadratne fukncije . Nacrtas grafik kvadratne fukncije 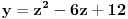 , grafik je definisan u intervalu , grafik je definisan u intervalu 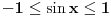 . Sa tog grafika ucitas max i min vrednost. . Sa tog grafika ucitas max i min vrednost.[ devetkamp @ 29.12.2011. 20:08 ] @
1. Odrediti dimenzije prave kruzne kupe date zapremine V, tako da njena povrsina bude minimalna. HITNO !
[ edisnp @ 29.12.2011. 20:32 ] @
[ devetkamp @ 29.12.2011. 20:40 ] @
[ devetkamp @ 29.12.2011. 21:17 ] @
[ darkosos @ 30.12.2011. 08:03 ] @
Ne znam odakle ti tu x. Ono P koje si izracunao izgleda dobro, ostaje da se uradi izvod po H, jer ti je to promenljiva tu, i da se izjednaci sa nulom.
Mozda si mogao i H da zamenis sa izrazom po r, ne znam da li bi bilo jednostavniji izvod. U svakom slucaju zadatak je ovog tipa: V=V(r,H)=const, trazi se min funkcije P=P(r,H). Iz prve jednakosti, kao sto si i uradio, imas r=f(H) (a moze i H=g(r)) pa se zamenom dobija P=P(f(H),H). Trazenjem izvoda ove funkcije po H, dobijas te moguce ekstremne tacke. [ devetkamp @ 30.12.2011. 12:25 ] @
[ SrdjanR271 @ 30.12.2011. 14:50 ] @
Uprosti uvek izraz od koga tražiš izvod.
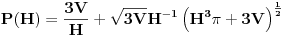  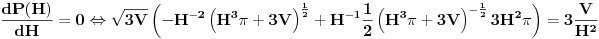 Množiš sve sa H^2 (3V)^(-1/2). 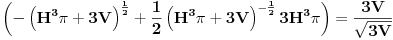 Smena H^3=t. 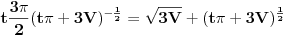 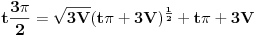 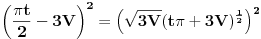 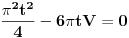 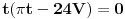 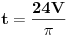 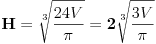 Da napomenem, mi ne znamo da li je u ovoj tački min ili max. Tačka (H, P(H)) je stacionarna tačka. Ispostaviće se da jeste min. Npr. drugi izvod  u tački u tački 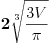 . .EDIT: H>0, za H=0 imamo krug, pa nisam komentarisao t=0. [Ovu poruku je menjao SrdjanR271 dana 30.12.2011. u 16:02 GMT+1] [Ovu poruku je menjao SrdjanR271 dana 30.12.2011. u 16:09 GMT+1] Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|