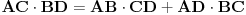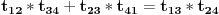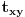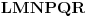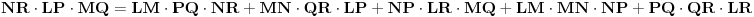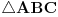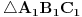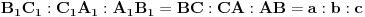[ sekretar SkOJ-a @ 07.05.2005. 19:31 ] @
| Tekst je sledeci: Date su cetri razlicite tacke na kruznici A, B, C, D u ovom redosledu. Ako se znaju razdaljine AC, BC, AD, BD treba naci CD. Prvo sto se uoci da je cetvorougao koji obrazuju ove tacke tangentni, zatim se mogu primeniti Heronove formule, sinusna , kosinusna teorema, medjutim kako god radio dobijem jednacine sa 4, 5 stepena sa 30-ak clanova koje treba skratiti itd. Posto je to ocigledno glup nacin, jer problem ne deluje toliko tezak, jel ima neko neku ideju kako da se efikasno resi ovaj problem ? Hvala unapred! |