Ja mislim da znam kako se resava al dobijem sistem u kome su odvratni tj. neresivi koeficijenti kao npr. koren((8*koren(154)+743)/154) i slicno...

Ima li neko neku pomoc? :)

Da ovo standardan tip samo sto su navedene ravni dosta pipave...
Naime, ja sam pre ove tipove zadataka radio na sledeci nacin:

(1) Nadjem oresecnu pravu datih ravni, npr p (vektor te prave kao vektorski proizvod normalnih vektora na date ravni, a tacku random)
(2) Uzmem bilo koju tacku, npr. A, sa prve ravni i proektujem je na p, npr u B. Zatim pustim normalu na p u B tako da pripada drugoj ravni i sa te prave opet uzmem random tacku C.
(3) Nadjem simetralu ugla ABC i ta prava i prava p daju trazenu ravan.

Počnimo od jednačina bisektrisa ovog diedarskog ugla. Ima ih 2. Kao što znamo jedna, od tih dveju ravni, će biti "simetrala" oštrog, a druga tupog ugla. Baš kao u 2D slučaju. Baš kao i u 2D slučaju ćemo rešavati.

Sve tačke "simetrale" će biti podjednako udaljene od obe ravni, tj, ako sa M(x,y,z) obeležimo opštu tačku, vidimo da je uslov da M pripada bilo kojoj od bisektralnih ravni


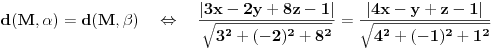
tj


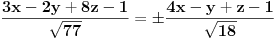
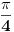
Ponovo, to su dve ravni, međusobno normalne. Ako jedna od njih zaklapa sa bilo kojom početnom ravni oštar ugao manji od , to je ravan koju želimo. Sad, istina, mi ne možemo tek tako izračunati ugao između dve ravni, ali možemo cosinus tog ugla.
Označimo sa


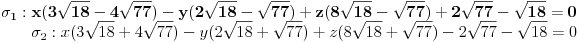
Vektor prve izračunate ravni je

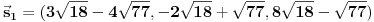
a nj intenzitet


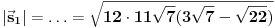
Do ugla između prve izračunate i druge zadate ravni dolazimo putem ugla između nj vektora.

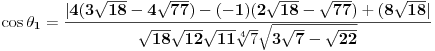
tj

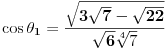
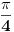
kad ovo uporedimo sa vidimo da je


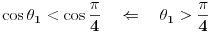
Dakle to nije naša ravan. Naša ravan je ona druga, tj bisektralna ravan je


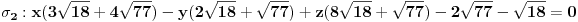
Daklem, zadatak nije težak, no su brojevi malo iracionalni.

Hvala ti, nisi se trebao toliko truditi. Skontao sam i sam da su koeficijenti bolesno iracionalni.
Jos jednom hvala