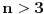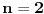Neka svako od njih isece sebi 1/3 pizze.

Kako zamisljas da onaj poslednji od njih isece trecinu te pice?

Je l' dosta 3 algoritma? :)

1) Pica se zaseče na jednom mestu i nož se vrti iz centra pice polako ukrug. Kada neka osoba bude zadovoljna parčetom koje bi se dobilo kada bi se pica presekla tamo gde se nož trenutno zadesi uzvike: "Stop!". Tada se to parče iseče i da se osobi koja je uzviknula, i postupak se nastavlja. Ukoliko dve ili više osoba viknu istovremeno parče se daje bilo kojoj od njih.

2) Prva osoba iseče n-ti deo pice (po sopstvenoj proceni). Zatim se odsečeno parče kreće od osobe do osobe i svako ko misli da je veće od n-tog dela može da odseče "višak". Poslednja osoba može da uzme parče ako želi, u suprotnom parče ide poslednjoj osobi koja je sekla. Ostatak ponavljamo bez osobe koja je dobila parče.

3) Ovaj je možda najkomplikovaniji. Prva osoba uzme kod sebe celu picu. Neka broj k uzima vrednosti od 2 do n. U svakom koraku se dešava sledeće: prvih k-1 osoba iseče svoj deo na k delova, a zatim k-ta osoba sebi uzme jedan od njih.

To bi bilo to, ali ovo pitanje poteže još jedno: iako je svaka osoba ovde uverena da može sebi da uzme bar n-ti deo pice, može li se smisliti takav algoritam koji će garantovati još i da nijedna druga osoba ne dobije više? Ovo je mnogo teži problem i algoritam koji sledi je za 3 osobe (kako ide za više ne znam):

a) Prva osoba podeli picu na 3 jednaka dela;
b) Druga osoba od najvećeg dela odstrani toliko koliko je potrebno da ostatak bude jednak sa srednjim delom;
c) Treća osoba bira parče. Ako ostavi "skraćivano" parče onda ga uzima druga osoba, u suprotnom druga osoba bira jedno od preostalih. Prva osoba dobija ono što ostane.
d) Druga ili treća osoba ima "skraćivano" parče - neka je to osoba P, a ona koja ga nema osoba Q. Osoba Q deli "višak" iz koraka b) na 3 dela od kojih po jedan biraju P, prva osoba, Q, redom.

To bi bilo to, ima li pitanja? :)

Dobri su metodi :) Malo suvise teoretski, ali drugacije bas i ne ide.

Prva metoda je surova, greedy. Zamisli kada se noz okrece i pocnes razmisljati da ce neko reci stop pre tebe. Na kraju kazes stop pa ipak nisi zadovoljan :) Ali se slazem da je pravedna.

Drugu metodu nisam bas razumeo. Recimo da ima 3 osobe. Prva osoba isece trecinu. Druga osoba misli da je to previse i presece to na pola. Treca osoba naravno to ne zeli. Onda prakticki ta sestina ide prvoj osobi?

Treca metoda mi se cini najpravednija. Samo mislim da bi bila dosta komplikovana za .

Sve u svemu, ima pravednih metoda, ali nisam siguran da bi svi bili zadovoljni. Tako je to i za :)

Prvi isece picu na tri dela. Zatim, drugi odredi koje parce ce pripasti prvom.
Posle toga treci od preostala dva parceta bira jedno za sebe. Ukoliko drugi nije
zadovoljan svojim parcetom, odsece deo parceta treceg. Treci onda izabere da
li hoce parce koje mu je ostalo odsecanjem, ili parce drugog zajedno sa odsecenim
viskom.

Mislim da je ovo najprostije resenje za slucaj sa trojicom.

Ne, nisi dobro shvatio (moguće da sam se ja loše izrazio), štaviše meni se ta druga metoda najviše sviđa. Znači, ako poslednja osoba ne želi parče onda parče ide poslednjoj osobi koja je sekla, odnosno u tvom slučaju drugi dobije svoju željenu šestinu.

Možda je najprostije, ali ne valja :) Recimo da prvi preseče picu na pola, a preostalu polovinu podeli na još dva dela, i onda drugi da prvom pola pice (npr. zato što su braća ;)). Treći tad svakako neće biti zadovoljan.