Mislim da znam nekog ko zna

Dobro, hoće li neko da odgovori, ili moram ja?

Ako nekoga zanima, mogu da postujem jedan algoritam.

Ja se lično ne bavim Galoaovim grupama ali ako te ne mrzi napiši taj algoritam koji znaš, možda će nekome nekad zatrebati.

Ja bih voleo da vidim, s tim da necu moci da ga detaljnije analiziram narednih 20-tak dana, jer trenutno radim druge stvari.

Polje algebarskih brojeva je rekurzivno. To znači da postoji reprezentacija algebarskih brojeva, tako da se može algoritamski računati sa njima (množiti, deliti, sabirati, oduzimati i porediti da li su jednaki), baš kao što racionalni brojevi imaju reprezentaciju (par - brojilac, imenilac) takav da postoje pravila računanja sa time.

Pošto je algebarski broj koren polinoma stepena bar jedan sa racionalnim koeficijentima, može se kao reprezentacija izabrati par - polinom, disk čiji centar ima racionalan realan i imaginaran deo i racionalan poluprečnik takav da željeni koren polinoma pripada unutrašnjosti diska, a ostali ne pripadaju zatvorenju diska.

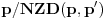
Pritom se lako može osloboditi najpre višestrukih korena polinoma, jer polinom ima isti skup korena kao polinom , ali je svaki jednostruk. Time prelazimo na slučaj kada nam je broj korena polinoma poznat (jednak stepenu polinoma). Dalje, postoje globalno konvergentni algoritmi za numeričko rešavanje algebarskih jednačina. To znači da možemo odrediti onoliko proizvoljno malih disjunktnih diskova koji sadrže po jedan koren, koliki je stepen polinoma. Time se svi koreni polinoma mogu izračunati sa proizvoljnom tačnošću.

Računanjem vrednosti izraza u tački koja je neki od tih korena uzimajući u obzir disk kome koren pripada i grešku odsecanja prilikom računanja može se odrediti disk kome pripada vrednost izraza, pri čemu taj dosk može biti po želji mali s tim da se odredi dovoljno mali disk kome pripada taj koren. Takođe, algoritmima za faktorizaciju, kao što je na primer Kronekerov, može se polinom faktorisati na proste činioce nad poljem . Ako se svaki od faktora izračuna u tački koja predstavlja željeni koren i dobije disk kome pripada željena vrednost, dobijanjem sve manjih diskova će se dobiti za sve faktore osim jednog da im taj koren polaznog polinoma nije koren, na osnovu čega je taj koren polaznog polinoma koren preostalog faktora. Tako se u reprezentaciji može preći na nesvodljiv polinom nad poljem .

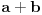
Problem je kako na osnovu reprezentacija algebarskih brojeva i izračunati reprezentaciju od npr. i slično za oduzimanje, delenje, množenje i korenovanje proizvoljnog stepena.

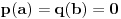
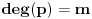
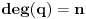
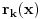
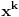
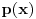
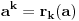
Ako je , pri čemu je i , onda se svaki stepen broja može prikazati kao linearna kombinacija stepena broja sa izložiocima manjim od i sa racionalnim koeficijentima. Naime, ako je ostatak pri delenju polinoma polinomom , onda je . Slično važi i za stepene broja .

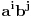
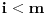
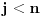
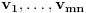
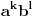
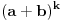
Uočimo brojeve , gde je i i numerišimo ih i označimo sa . Svaki broj oblika se može prikazati kao linearna kombinacija brojeva sa racionalnim koeficijentima. Korišćenjem te činjenice i binomne formule se može broj izraziti kao linearna kombinacija brojeva sa racionalnim koeficijentima.

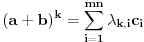
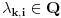
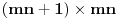
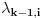
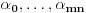
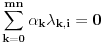
Ako je uz , formirajmo matricu formata takvu da se u preseku -te vrste i -te kolone nalazi . Obzirom da je broj vrsta veći od broja kolona, vrste matrice su linearno zavisne, postoje racionalni brojevi od kojih barem jedan nije nula, takvi da je za svako . Stoga je

,

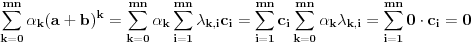
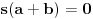
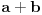
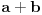
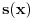
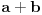
odnosno za . Slično se postupa u slučaju ostalih operacija. Nakon što smo odredili nenula polinom sa racionalnim koeficijentima čiji je jedan od korena treba odrediti bar jedan disk u čijoj unutrašnjosti leži i čijem zatvorenju ne pripada nijedan drugi koren polinoma . 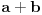To se može učiniti sve tačnijim izračunavanem brojeva i u cilju sve tačnijeg izračunavanja broja i sve tačnijim računanjem svih korena polinoma sve dok disk koji sadrži ne postane disjunktan sa diskovima koji sadrže korene polinoma osim jednog.

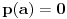
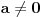
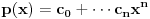
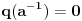
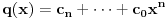
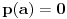
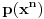
Slično se postupa i sa oduzimanjem i množenjem. Što se inverza u odnosu na množenje tiče, ako je za i , onda je za . Takođe, ako je bilo koji -ti kompleksni koren broja i , onda je koren polinoma . Za određivanje diskova važe slične primedbe kao malopre.

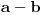
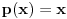
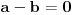
Napokon, kako utvrditi da li su brojevi i dati različitim reprezentacijama jednaki? Izračunajmo reprezentaciju broja , pa ako se posle svođenja polinoma iz reprezentacije na minimalan dobije polinom , onda je , a u suprotnom nije.

_{[Ovu poruku je menjao Nedeljko dana 13.05.2013. u 21:51 GMT+1]}

Proverimo koliko su ključne teoreme Galoaove teorije konstruktivne do na rekurzivnost polja algebarskih brojeva. Ispostaviće se da jesu.

Neka je dat polinom sa racionalnim koeficijentima stepena barem jedan. Polinomi i imaju isti skup korena, pa samim tim i isto korensko polje, pa samim tim i istu Galoaovu grupu, pri čemu drugi nema višestrukih korena. Stoga se možemo ograničiti na slučaj polinoma bez višestrukih korena.

Ako su svi koreni polinoma bez višestrukih korena uzeti po jedanput (njihove reprezentacije su izračunljive na osnovu polinoma ), treba naći koje je primitivni element korenskog polja polinoma . U tu svrhu koristimo algoritam iz teoreme o primitivnom elementu. Ako su i algebarski brojevi dati reprezentacijama, postoji primitivan element oblika , gde je izabrano tako da ne zadovolji nijednu od nekih konačno mnogo linearnih jednačina sa koeficijentima koji su algebarski brojevi kojima možemo naći reprezentacije. Računajući sa reprezentacijama, za jedan po jedan ceo broj proveravamo da li ispunjava uslove dok ne nađemo onaj koji ispunjava. Tako nalazimo reprezentacije brojeva takvih da je i za . U tom slučaju je traženi primitivni element.

Obzirom da imamo reprezentaciju elementa , a ona se uvek može svesti na slučaj kada je polinom u reprezentaciji nesvodljiv nad poljem racionalnih brojeva, imamo i minimalni polinom primitivnog elementa. Numeričkim nalaženjem korena tog polinoma nalazimo i reprezentacije svih konjugata od . Recimo da su svi oni i da je .

Automorfizmi korenskog polja (koje je Galoaovo raširenje osnovnog polja) slikaju algebarski broj u neki od njegovih konjugata, mogu ga preslikati u bilo koji od konjugata i jednoznačno su određeni slikom primitivnog elementa. Recimo da je automorfizam za koji je . Pitanje je šta je . Svakako mora biti u pitanju jedan od brojeva . Ako je polinom sa racionalnim koeficijentima takav da je , onda je . Obzirom da ova vrednost mora pripadati konačnom skupu , numeričkim računanjem možemo poodbacivati sve mogućnosti osim jedne i zaključiti koliko je .

Ostaje da se odredi polinom . On se može odrediti tako što se nabrajaju svi polinomi sa racionalnim koeficijentima stepena nižeg od dok se ne nađe onaj čija je vrednost u tački jednaka . Naravno, ima i efikasnijih načina, ali i ovo je dovoljno za konstrukciju algoritma, koliko god on bio neefikasan.

Postoji još nešto - ako se ispostavi da je Galoaova grupa rešiva, postoji algoritam koji ispisuje radikalska rešenja. Pristup je opet u tome da se slede ključne teoreme Galoaove teorije, čiji su standardni dokazi konstruktivni do na rekurzivnost polja algebarskih brojeva, ali je priča kudikamo duža i zaista me mrzi da pišem. U svakom slučaju bih voleo da čujem druge šta misle o ovome.

Ispravka:

Umesto treba .