[ Srđan Krstić @ 12.05.2005. 21:52 ] @
| Posto vidim da je bilo dosta tema u kojima se trazi pomoc iz oblasti teorije algoritama, a nisam video ovakav tutorial kao TOP temu, evo svega sto mi trenutno pada na pamet: |
|
[ Srđan Krstić @ 12.05.2005. 21:52 ] @
[ Srđan Krstić @ 12.05.2005. 21:53 ] @
Strukture Podataka (Data structures):
Za implementaciju vecine algoritama od presudnog je znacaja struktura podataka koja se koristi. Cak, mnogi problemi ne bi se ni mogli resiti bez primene odgovarajuce strukture podataka. Povezana lista Povezana lista (linked list) je nista drugo nego niz elemenata, od kojih svaki ima 2 polja. U jednom je vrednost elementa (ono sto bi bilo na tom mestu u obicnom nizu), a u drugom pokazivac na sledeci element niza. Zadnji element pokazuje na NULL.  Prednosti ovakve strukture podataka su ubacivanje i izbacivanje elemenata iz liste u vremenskoj slozenosti 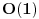 . .http://people.cs.uct.ac.za/~bm...ual/structures/linkedlist.html http://gethelp.devx.com/techtips/cpp_pro/10min/10min0599.asp Stek Stek (stack) je LIFO (Last In First Out) lista. Naime, kada treba smestiti novi element u stek, on se stavlja na njegov kraj (PUSH operacija), pri cemu se i pri uzimanju elemenata sa steka oni takodje uzimaju sa kraja (POP operacija). Stek inace koristi i sam kompajler pri rekurziji, tako da je jedna od primena steka bas simuliranje rekurzije. http://people.cs.uct.ac.za/~bmerry/manual/structures/stack.html Red Red (queue) je FIFO (First In First Out) lista. U ovu listu se elementi stavljaju na kraj, ali uzimaju sa pocetka (kao red u prodavnici). Najbitnija primena reda je u Breadth First Search (BFS) algoritmu. http://people.cs.uct.ac.za/~bmerry/manual/structures/queue.html Hash tablice Hash tablice (hash tables) nastaju hashiranjem elemenata. Naime, svaki element koji zelimo smestiti u ovu strukturu podataka hashiramo, tj. sracunamo vrednost koju neka hash funkcija daje za njega, i smestimo na to mesto u tabelu. Primer: Treba zapamtiti imena ucenika nekog razreda i jos neki podatak o svakom, recimo broj telefona. Primer hash funkcije je recimo zbir ascii vrednosti svih slova u imenu po modulu velicine tablice (sto je najpozeljnije neki prost broj). Ako je to mesto vec zauzeto, dodajemo jos jedan unos u isto polje (mozemo hash tablicu dakle pamtiti kao matricu, ili kao niz povezanih listi, sto je bolja implementacija). Sada kad trebamo naci Markov broj telefona, sabracemo ascii vrednosti slova u reci "Marko", uzeti tu vrednost po modulu velicine tablice, i traziti na tom mestu u hash tablici. Prednost ove strukture podataka je vreme pristupa elementu 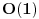 . .http://people.cs.uct.ac.za/~bmerry/manual/structures/hash.html http://ciips.ee.uwa.edu.au/~morris/Year2/PLDS210/hash_tables.html Drvo Za one koji su upoznati, drvo (tree) predstavlja graf koji nema nijedan krug (ciklus). Koncepcija ove strukture podataka je vec i iz samog imena jasna, a narocito uz sliku:  Za neki pocetni cvor kazemo da je "koren" (root) drveta, za svaki cvor one koji su "nadole" od njega i direktno povezani sa njim kazemo da su njegova "deca" (children), a zajedno sa onima nadole sa kojima je povezan preko vise od jedne ivice kazemo da su njegovi "potomci" (descendants). Svaki cvor koji je "nagore" od nekog i povezan sa njim je njegov "predak" (ancestor). Neki cvor zajedno sa svim njegovim potomcima cini poddrvo (subtree) ciji je on root. Najcesce se koristi binarno drvece, u kome svaki cvor ima najvise dvoje dece. Takodje, ovde svaki cvor ima svoje levo i desno poddrvo. http://people.cs.uct.ac.za/~bmerry/manual/structures/tree.html Binarno drvo pretrage Binarno drvo pretrage (binary search tree) je takvo drvo u kome je za neki cvor njegovo levo dete uvek manje od njega, a desno uvek vece. U ovakvom drvetu je za trazenje ubacivanje ili izbacivane nekog elementa potrebno vreme 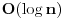 . Medjutim, ako su elementi lose rasporedjeni, svaka od ovih operacija moze odneti cak . Medjutim, ako su elementi lose rasporedjeni, svaka od ovih operacija moze odneti cak 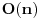 vremena! vremena!http://www.cs.mcgill.ca/~cs251/OldCourses/1997/topic9/ http://www.cs.nyu.edu/algvis/java/bst.html http://www.personal.kent.edu/~...lgorithms/binarySearchTree.htm AVL drvo AVL drvo je "izbalansirano" binarno drvo pretrage. U njemu je razlika visina levog i desnog poddrveta za svaki cvor najvise 1. Naime, pri svakom dodavanju ili izbacivanju elemenata, obraca se paznja da drvo ostane izbalansirano kao sto je receno, pri cemu se za taj korak ne sme potrositi vise od 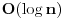 vremena. Slozenosti svih operacija su kod ovakvog drveta uvek tacno vremena. Slozenosti svih operacija su kod ovakvog drveta uvek tacno 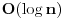 . .http://www.cmcrossroads.com/br...ftp/src/libs/C++/AvlTrees.html http://ciips.ee.uwa.edu.au/~morris/Year2/PLDS210/AVL.html http://cis.stvincent.edu/swd/avltrees/avltrees.html Heap Heap je jos jedna vrsta binarnog drveta, kod koga je zadovoljen uslov da su deca svakog cvora uvek veca ili jednaka od samog tog cvora (moze se praviti i obrnuto, da su deca uvek veca od oca). Ova struktura podataka ima izuzetno sirok spektar upotrebe. Naime, cesto je potrebno u svakom trenutku znati koji je najmanji element nekog niza. Koristeci heap, ovu informaciju imamo u 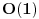 (to je ustvari prvi element u heap-u). Updateovanje heap-a, sto ce reci izbacivanje ili ubacivane elementa radi se u (to je ustvari prvi element u heap-u). Updateovanje heap-a, sto ce reci izbacivanje ili ubacivane elementa radi se u 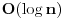 . Jedni od najpoznatijih algoritama u kojima se koristi heap su Dijkstrin i Primov algoritam, o kojima ce biti reci kasnije. . Jedni od najpoznatijih algoritama u kojima se koristi heap su Dijkstrin i Primov algoritam, o kojima ce biti reci kasnije.http://people.cs.uct.ac.za/~bmerry/manual/structures/heap.html http://ciips.ee.uwa.edu.au/~morris/Year2/PLDS210/heaps.html http://planetmath.org/encyclopedia/Heap.html Kumulativne tabele Zadat je niz od n elemenata i nad njime treba vrsiti 2 operacije: jedna je povecaj (i, x), sto znaci povecaj i-ti element za x, a druga je Sum (i), koja treba da vraca zbir prvih i elemenata niza. Koriscenje trivijalnih struktura podataka bi dovelo do slozenosti 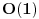 za jednu, za jednu, 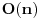 za drugu operaciju. Primenom kumulativnih tabela, obe operacije vrse se u za drugu operaciju. Primenom kumulativnih tabela, obe operacije vrse se u 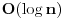 . Detaljno objasnjene nacina rada kumulativnih tabela, sa kodovima. . Detaljno objasnjene nacina rada kumulativnih tabela, sa kodovima.http://www.elitesecurity.org/poruka/519118 http://www.cs.ubc.ca/local/rea...95/spe/vol24/issue3/spe884.pdf Struktura za nalazene unije Union find problem se sastoji u tome da imamo neke elemente, i treba da vrsimo dve operacije: da kazemo u kojoj se grupi nalazi neki element, i da spojimo (napravimo uniju) dve grupe. To radimo tako sto neke elemente obelezimo kao "predstavnike", s tim da svaka grupa ima najvise jednog predstavnika. Takodje, svaki element x ima pridruzenu vrednost link [x], gde prateci linkove dodjemo konacno do predstavnika grupe u kojoj se nalazi taj element. Za spajanje dve grupa A i B, jednostavno predstavnika grupe A proglasimo da vise nije predstavnik, a njegov link postavimo na predstavnika B. Dobrom implementacijom dobija se slozenost ovih operacija 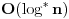 , sto je skoro konstantno. , sto je skoro konstantno.http://www.cs.berkeley.edu/~luca/cs170/notes/lecture12.pdf Strukture podataka kod grafova U grafovskim algoritmima za razlicite probleme mogu se koristiti sve navedene strukture podataka, nezavisno od toga sto se problem odnosi bas na graf. Ovde cu samo napomenuti strukture za predstavaljnje samog grafa, tj. njegovih cvorova i ivica. Jedan nacin je matrica povezanosti, nazovimo je edge, gde je edge [i, j] = 1 akko postoji ivica od cvora i do cvora j, a u suprotnom je 0. Drugi cesto koriscen nacin predstavljanja je lista suseda, gde za svaki cvor pamtimo listu svih njegovih suseda. [ Srđan Krstić @ 12.05.2005. 21:59 ] @
Searching & sorting:
Pretpostavimo da treba naci neki element u nekom nizu (dakle naci gde se nalazi, ili ustanoviti da ga nema). Nacin na koji cemo to uraditi najvise zavisi od toga kako smo taj niz zapamtili, tj. koju smo strukturu podataka upotrebili. Trazenje u hash tablicama Ako koristimo hash tablice, trazenje elementa je vrlo jednostavno. Samo ga treba "pluggovati" u hash funkciju i time ga nadjemo u 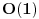 . . http://people.cs.uct.ac.za/~bmerry/manual/structures/hash.html http://ciips.ee.uwa.edu.au/~morris/Year2/PLDS210/hash_tables.html Trazenje u binarnom drvetu pretrage i AVL drvetu I ove strukture podataka, kao i hash tablice, su takve da im je jedna od poenti upravo trazenje elemenata. Kod obe je proces isti: podjemo od root-a celog drveta. Ukoliko je on element koji trazimo, kraj. Ako ne, vidimo da li je element koji trazimo manji ili veci od njega. Ako je manji, isti postupak (rekurzivno) ponavljamo za levo poddrvo, ako je veci za desno. Kao sto je vec receno, slozenost je 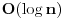 , sa tim da u nebalansiranom drvetu moze da bude i znatno gora (ali i bolja!). , sa tim da u nebalansiranom drvetu moze da bude i znatno gora (ali i bolja!).http://www.cs.mcgill.ca/~cs251/OldCourses/1997/topic9/ http://www.cs.nyu.edu/algvis/java/bst.html http://www.personal.kent.edu/~...lgorithms/binarySearchTree.htm http://www.cmcrossroads.com/br...ftp/src/libs/C++/AvlTrees.html http://ciips.ee.uwa.edu.au/~morris/Year2/PLDS210/AVL.html http://cis.stvincent.edu/swd/avltrees/avltrees.html Linearna pretraga Pretpostavimo da imamo obican niz od n elemenata. Linearna pretraga se sastoji u tome da prodjemo sve elemente niza trazeci onaj koji nam treba. Slozenost: 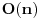 . .Binarna pretraga Imamo sortiran (rastuce) niz od n elemenata u kome treba naci neki. Neka je na pocetku left=1 i right=n. U svakoj iteraciji, nadjemo element middle kao srednji izmedju left i right. Ukoliko je trazeni element jednak tom middle, kraj. Ako je middle veci od njega, kazemo right=middle, u suprotnom left=middle, i ponavljamo isti postupak. Vrlo jednostavan, ali vrlo cesto upotrebljavan koncept. Slozenost je, naravno, 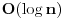 http://en.wikipedia.org/wiki/Binary_search http://planetmath.org/encyclopedia/BinarySearch.html Drugi problem koji razmatramo je jedan od najbolje proucenih problema u teoriji algoritama. To je sortiranje niza, a evo i nekoliko poznatijih algoritama: Selection, Insertion i Bubble Sort Ovo su tri vrlo jednostavna algoritma za sortiranje elemenata. Svi su izuzetno jednostavni, ali slozenosti 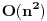 , pa zbog ih njihove banalnosti i neprakticnosti necu ni opisivati. Ako nekog interesuje kako koji radi, tu su linkovi. , pa zbog ih njihove banalnosti i neprakticnosti necu ni opisivati. Ako nekog interesuje kako koji radi, tu su linkovi.http://linux.wku.edu/~lamonml/algor/sort/selection.html http://linux.wku.edu/~lamonml/algor/sort/insertion.html http://linux.wku.edu/~lamonml/algor/sort/bubble.html Quick Sort Verovatno najbolji algoritam za sortiranje. Radi po sledecem principu: odredimo neki, bilo koji, element da bude pivot. Sada ispremestamo sve elemente niza tako da su prvo svi oni manji, pa onda svi oni veci od pivota. Sada, za svaki od ova dva dela rekurzivno pozovemo quicksort. Izuzetno elegantan i praktican algoritam, a lak za kodiranje. Slozenosti je 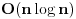 , mada ona nije uvek ista. U najgorem mogucem slucaju ona moze biti i , mada ona nije uvek ista. U najgorem mogucem slucaju ona moze biti i 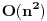 , medjutim, u praksi, quicksort obicno daje bolje rezultate od svih ostalih algoritama za sortiranje. U attachmentu je moj proggy koji demonstrira kako quick radi brze od heap i merge sorta na random nizu od 10000000 elemenata. , medjutim, u praksi, quicksort obicno daje bolje rezultate od svih ostalih algoritama za sortiranje. U attachmentu je moj proggy koji demonstrira kako quick radi brze od heap i merge sorta na random nizu od 10000000 elemenata.http://linux.wku.edu/~lamonml/algor/sort/quick.html http://www.csse.monash.edu.au/~lloyd/tildeAlgDS/Sort/Quick/ http://www.personal.kent.edu/~...gorithms/Sorting/quickSort.htm http://ciips.ee.uwa.edu.au/~morris/Year2/PLDS210/qsort.html http://www.codeguru.com/Cpp/Cp...rithms/sort/article.php/c5109/ Merge Sort Merge Sort radi na principu “podeli i vladaj”. On naime podeli niz na dva dela, rekurzivno se poziva za oba, a kada se vrati, ta dva dela spaja (merge) u jedan sortirani. Slozenost je uvek 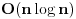 . Merge sort se jos moze i koristiti za racunanje broja inverzija permutacije, uz par redova dodatih u trenutku kada se nizovi spajaju. . Merge sort se jos moze i koristiti za racunanje broja inverzija permutacije, uz par redova dodatih u trenutku kada se nizovi spajaju.http://linux.wku.edu/~lamonml/algor/sort/merge.html http://www.cs.princeton.edu/~a...anim/gawain-4.0/MergeSort.html Heap Sort Heap Sort niz sortira tako sto ga smesti u heap. Vec znamo da operacije umetanja i skidanja sa heapa imaju slozenost 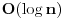 . Dakle ovaj algoritam ce imati ukupnu slozenost . Dakle ovaj algoritam ce imati ukupnu slozenost 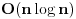 , jer svaki element treba prvo da ubacimo u heap, pa kad smo formirali ceo, izbacujemo uvek prvi element dokle god ne ispraznimo heap. , jer svaki element treba prvo da ubacimo u heap, pa kad smo formirali ceo, izbacujemo uvek prvi element dokle god ne ispraznimo heap.http://linux.wku.edu/~lamonml/algor/sort/heap.html http://ciips.ee.uwa.edu.au/~morris/Year2/PLDS210/heapsort.html http://www.csse.monash.edu.au/~lloyd/tildeAlgDS/Sort/Heap/ http://www.personal.kent.edu/~...lgorithms/Sorting/heapSort.htm Bucket Sort Pretpostavimo da imamo niz od n elemenata, ali u kome je svaki ceo broj izmedju 1 i m. Napravimo m "bucket"-a, tako da svakom broju odgovara po jedan. Prvo svaki element stavimo u njemu odgovarajuci bucket. Sada prodjemo kroz sve bucket-e jos jednom da bi napravili sortirani niz. Slozenost je 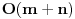 . Ukoliko je m mali broj ( . Ukoliko je m mali broj (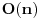 ), slozenost je linearna. Ako je pak m veliko, i slozenost je velika, a i problem je napraviti m bucketa (zbog kolicine potrebnog prostora). ), slozenost je linearna. Ako je pak m veliko, i slozenost je velika, a i problem je napraviti m bucketa (zbog kolicine potrebnog prostora).http://www.personal.kent.edu/~...orithms/Sorting/bucketSort.htm http://www.ics.uci.edu/~eppstein/161/960123.html Radix Sort Radix Sort ima slicnu ideju kao bucket. Naime, on prvo napravi samo 10 bucket-a (ako radimo u brojnom sistemu sa osnovom 10), i smesti svaki element u odgovarajuci bucket. Sada u svakom bucketu imamo veliki broj elemenata, i oni nisu sortirani medjusobno, ali svi imaju istu prvu cifru. Sada mozemo primeniti isti postupak na elementa svakog bucket-a, s tim sto umesto prve razmatramo drugu cifru. Onda to isto za trecu, itd. Slozenost je 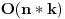 , gde je k broj cifara koliko imaju elementi tog niza. , gde je k broj cifara koliko imaju elementi tog niza.http://ciips.ee.uwa.edu.au/~morris/Year2/PLDS210/radixsort.html http://www.csse.monash.edu.au/~lloyd/tildeAlgDS/Sort/Radix/ http://www.cubic.org/docs/radix.htm Postoji teorema koja dokazuje "lower bound for sorting", tj. donju granicu slozenosti algoritama za sortiranje, koji kaze da je najbolje vreme za koje algoritam moze da sortira niz u opstem slucaju bas 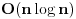 . To znaci da je za neke specijalne slucajeve moguce i bolje vreme, ali ne i generalno. Recimo radix moze raditi dosta brzo ako je broj cifara vrlo mali, ali broj cifara isto tako moze otici i u beskonacnost. Quick moze da radi za neke rasporede elemenata i dosta brze od . To znaci da je za neke specijalne slucajeve moguce i bolje vreme, ali ne i generalno. Recimo radix moze raditi dosta brzo ako je broj cifara vrlo mali, ali broj cifara isto tako moze otici i u beskonacnost. Quick moze da radi za neke rasporede elemenata i dosta brze od 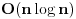 , ali ce za najgori slucaj raditi u , ali ce za najgori slucaj raditi u 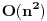 . Dakle, najbolje prosecno vreme rada nekog algoritma je . Dakle, najbolje prosecno vreme rada nekog algoritma je 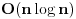 . Nesto o tome: . Nesto o tome:http://planetmath.org/encyclopedia/LowerBoundForSorting.html http://www.brpreiss.com/books/opus4/html/page514.html [Ovu poruku je menjao IsrkiboyI dana 13.05.2005. u 21:19 GMT+1] [ --SOULMaTe-- @ 13.05.2005. 14:44 ] @
Pohvale za ovaj potez!!!
[ Srđan Krstić @ 13.05.2005. 20:13 ] @
Dinamicko programiranje (dp) je princip kojim se resavaju mnogi problemi. Znaci nije kao npr. teorija grafova, gde imamo skup algoritama koji se odnose konkretno na grafove, vec je dp sam princip (stavise, mnogi se algoritmi recimo bas u teoriji grafova i oslanjaju na dinamicko programiranje). Dp se primenjuje u problemima koji imaju optimalnu podstrukturu. To znaci, ako treba resiti neki problem za n, mi cemo resiti probleme za 1, 2, ..., n-1, i, konacno, za n. Naravno ovo ne pali uvek, pa je zato i potrebno da problem ima gore pomenutu optimalnu podstrukturu. Uglavnom su to problemi gde se trazi neko optimalno resenje, dakle, nesto maksimalno ili minimalno. Dp neodoljivo podseca (a i jeste) na matematicku indukciju. Uzmimo banalan primer: treba naci najveci od n elemenata. Mi cemo naci najveci od 1 elementa (to je on sam). Kad imamo najveci od prvih k elemenata, nacicemo najveci od prvih k+1, tako sto cemo k+1-vi element uporediti sa dosadasnjim najvecim (od prvih k), pa ako je veci, uzimamo njega, ako ne, uzimamo onaj koji je bio najveci od prvih k. Na taj nacin cemo dobiti i najveci od svih n.
Kao sto rekoh, mnogi se algoritmi oslanjaju na dinamicko programiranje. Zato cu ja ovde navesti samo nekoliko njih, koji se ne mogu svrstati u ostalea kategorije koje cu opisati (namely, grafovski i geometrijski algoritmi). Problem ranca Problem ranca (knapsack problem) je verovatno najpoznatiji primer dinamickog programiranja. Postoji puno varijacija na temu ovog problema, a ja cu ovde navesti onu koju (bar ja) smatram za osnovnu. Imamo ranac u koji moze stati N zapreminskih jedinica. Imamo M predmeta, od koji svaki ima svoju zapreminu (Z) i vrednost (V). Treba naci optimalno popunjivanje ranca. Vec na prvi pogled je jasno da grabljivi (greedy) algoritam ovde ne pali. Ne mozemo uzimati predmete sa sto manjom zapreminom, jer je moguce da neki od njih imaju isuvise malu vrednost, pa nam se ne isplati. Isto tako ne mozemo uzimati ni predmete sto vece vrednosti, jer mogu imati isuvise veliku zapreminu. Ono sto moze da nam se ucini na prvi pogled, to je da treba uzimati elementa ciji je odnos vrednost/zapremina sto veci. Ali, ni ovo nije tacno! Uzmimo primer: imamo ranac velicine 8, i tri predmeta: jedan zapremine 6 i vrednosti 7, i dva zapremine po 4 i vrednosti po 4. Najveci odnos vrednost/zapremina ima prvi predmet, ali ako uzmemo njega, ne mozemo staviti vise ni jedan predmet u ranac, pa ce ukupna vrednost biti 7. Sa druge strane, uzmemo li druga dva predmeta, imacemo vrednost 8! Zato pribegavamo dinamickom programiranju. Moramo utvrditi optimalnu podstrukturu problema. Punimo rance velicina 1, 2, ..., N redom. Ako smo optimalno popunili ranac velicine k, a poslednji stavljen element je recimo i-ti, onda je jasno da izabrani predmeti (bez i-tog) optimalno popunavaju ranac velicine 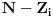 . Ovo je dovoljno da zakljucimo optimalnu podstrukturu! Ostaje jos samo da imamo neku "bazu indukcije", a to je ranac velicine 0, koji je optimalno popunjen kada u njemu nema nijednog predmeta (a i ne moze biti). Dakle, algoritam se svodi na to da idemo od 1 do N, i za svako i prodjemo brojacem j sve predmete, i proverimo da li je popunjavanje ranca velicine . Ovo je dovoljno da zakljucimo optimalnu podstrukturu! Ostaje jos samo da imamo neku "bazu indukcije", a to je ranac velicine 0, koji je optimalno popunjen kada u njemu nema nijednog predmeta (a i ne moze biti). Dakle, algoritam se svodi na to da idemo od 1 do N, i za svako i prodjemo brojacem j sve predmete, i proverimo da li je popunjavanje ranca velicine 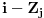 zajedno sa j-tim elementom bolje od trenutnog najboljeg popunjavanja ranca velicine i, tj. da li je zajedno sa j-tim elementom bolje od trenutnog najboljeg popunjavanja ranca velicine i, tj. da li je 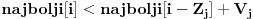 . Ako jeste, updateujemo tu vrednost. Tako cemo dobiti i optimalno popunjavanje ranca velicine N. Slozenost je ocigledno . Ako jeste, updateujemo tu vrednost. Tako cemo dobiti i optimalno popunjavanje ranca velicine N. Slozenost je ocigledno 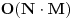 . .http://www.cs.toronto.edu/~heap/270F02/node62.html Najduzi zajednicki podniz Najduzi zejdnicki podniz (longest common subsequence) je problem u kome za dva niza treba odrediti najduzi koji je oboma podniz (elementi ne moraju biti uzastopni da bi cinili podniz, jedino je bitan redosled u kome se javljaju). Neka je prvi niz duzine n, drugi duzine m. Pravimo matricu best [i, j], koja predstavlja duzinu najduzeg podniza za prvih i clanova prvog niza, i prvih j clanova drugog niza. best [0, i] i best [i, 0] je 0 za svako i. Best [i, j] je best [i-1, j-1] + 1, ako su i-ti clan prvog i j-ti clan drugog niza jednaki, ili max (best [i-1, j], best [i, j-1]) ako su razliciti, za svako i od 1 do n i svako j od 1 do m. Best [n, m] je resenje problema. Primetimo da za best ne moramo koristiti matricu, jer u svakoj iteraciji koristimo samo prethodni i trenutni red te matrice, pa je dovoljno pamtiti samo 2 reda. Medjutim, ukoliko nam se trazi ne samo duzina najduzeg zajednickog podniza, vec i sam podniz, neophodno je pamtiti matricu, kako bismo mogli da rekonstruisemo "put" kroz matricu i sam niz. Slozenost algoritma je 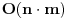 . .http://www.cs.pitt.edu/~kirk/cs1510/notes/dynnotes/node3.html http://ranger.uta.edu/~cook/aa/lectures/applets/lcs/lcs.html http://www.cs.fsu.edu/~cop4531/slideshow/chapter16/16-3.html Najduzi rastuci podniz Najduzi rastuci podniz (longest increasing subsequence) trazi najduzi rastuci rastuci podniz za dati niz, pri cemu podniz definisemo kao u prethodnom problemu. Ovo je (bar po meni) jedan od najlepsih problema koji se resavaju dinamicki. Za pocetak, primetimo da ovaj problem mozemo resiti tako sto cemo naci najduzi zajednicki podniz za dati niz i rastuce sortirani niz, sto bi vodilo slozenosti 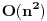 . Ali, mi hocemo bolje od ovoga. Pocecemo sa kraja niza i ici unazad (sto cesto pali kod dinamickog). Za svaki broj x, pamtimo vrednost best [x], koja predstavlja najveci broj koji je prvi u rastucem nizu duzine x. Primer, imamo niz: 3 6 4 9 8 10. Polazimo od 10 i idemo u nazad. Kad razmatramo recimo broj 4, best [2] je 9 (sto predstavlja podniz 9 10). Ovde se i krije optimalna podstruktura problema, jer, sigurno nam je bolje da uzmemo niz 9 10 i na njegov pocetak kalemimo elemente, nego na niz 8 10. Tako iduci ulevo, mozemo da "nakalemimo" pocetke niza, i updateujemo best vrednosti ako je potrebno. Jasno, po zavrsetku ce najveci index u best nizu koji je razlicit za koji smo nasli neku vrednost biti resenje. Slozenost ovog algoritma bi bila . Ali, mi hocemo bolje od ovoga. Pocecemo sa kraja niza i ici unazad (sto cesto pali kod dinamickog). Za svaki broj x, pamtimo vrednost best [x], koja predstavlja najveci broj koji je prvi u rastucem nizu duzine x. Primer, imamo niz: 3 6 4 9 8 10. Polazimo od 10 i idemo u nazad. Kad razmatramo recimo broj 4, best [2] je 9 (sto predstavlja podniz 9 10). Ovde se i krije optimalna podstruktura problema, jer, sigurno nam je bolje da uzmemo niz 9 10 i na njegov pocetak kalemimo elemente, nego na niz 8 10. Tako iduci ulevo, mozemo da "nakalemimo" pocetke niza, i updateujemo best vrednosti ako je potrebno. Jasno, po zavrsetku ce najveci index u best nizu koji je razlicit za koji smo nasli neku vrednost biti resenje. Slozenost ovog algoritma bi bila 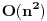 , jer za svaki element moramo proci ceo best niz. Naravno, cim dodjemo do nekog indexa u best nizu za koji nemamo upisano nista (dakle ne postoji rastuci podniz te duzine od dosad prodjenih elemenata), ne moramo nastavljati dalje, jer sigurno ne postoje ni duzi podnizovi, pa ce algoritam u sustini raditi i dosta brze u praksi. Medjutim, postoji cak i poboljsanje! Primetimo da je best niz sortiran! Zato, umesto linearne, mozemo koristiti binarnu pretragu da svakom elementu pronadjemo "mesto" u best nizu. Slozenost je onda , jer za svaki element moramo proci ceo best niz. Naravno, cim dodjemo do nekog indexa u best nizu za koji nemamo upisano nista (dakle ne postoji rastuci podniz te duzine od dosad prodjenih elemenata), ne moramo nastavljati dalje, jer sigurno ne postoje ni duzi podnizovi, pa ce algoritam u sustini raditi i dosta brze u praksi. Medjutim, postoji cak i poboljsanje! Primetimo da je best niz sortiran! Zato, umesto linearne, mozemo koristiti binarnu pretragu da svakom elementu pronadjemo "mesto" u best nizu. Slozenost je onda 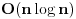 . Primetimo jos i da opisanim algoritmom mozemo samo naci duzinu podniza, a ne i sam podniz. Kao odlican reference o ovom problemu, prilazem u attachmentu text sa www.usaco.org. . Primetimo jos i da opisanim algoritmom mozemo samo naci duzinu podniza, a ne i sam podniz. Kao odlican reference o ovom problemu, prilazem u attachmentu text sa www.usaco.org.O dinamickom programiranju nemam jos mnogo stosta reci (algorithm-wise), jer je to, kao sto sam vec rekao, princip resavanja problema. Za dalji reference obratite se navedenim linkovima, a ako postoji interesovanje, mozda napisem posebnu temu posvecenu dinamickom programiranju. Obavezna literatura za ovu oblast je knjiga "Dinamicko programiranje" Milana Vugdelije. http://mat.gsia.cmu.edu/classes/dynamic/dynamic.html [Ovu poruku je menjao IsrkiboyI dana 15.05.2005. u 04:50 GMT+1] [ gpreda @ 13.05.2005. 23:04 ] @
Slazem se da ovaj topic treba da se stavi pod TOP.
Samo da dodam: Citat: Radix Sort Radix Sort ima slicnu ideju kao bucket. Naime, on prvo napravi samo 10 bucket-a (ako radimo u brojnom sistemu sa osnovom 10), i smesti svaki element u odgovarajuci bucket. Sada u svakom bucketu imamo veliki broj elemenata, i oni nisu sortirani medjusobno, ali svi imaju istu prvu cifru. Sada mozemo primeniti isti postupak na elementa svakog bucket-a, s tim sto umesto prve razmatramo drugu cifru. Onda to isto za trecu, itd. Slozenost je , gde je k broj cifara koliko imaju elementi tog niza. Kao sto si rekao, donja granica za sortiranje je O(n log n) za one algoritme koji su bazirani na poredjenu elemenata. Radix sort je drugaciji, kod njega nikada ne poredimo dva elementa niza, zato je kod njega donja granica slozenosti drugacija i to ga cesto cini veoma pogodnim u nekim algoritmima. Radix sort ima osobinu da je stabilan, to znaci da kada izvrsimo jedan korak sortiranja (po npr. jednoj decimali), dva elementa koja su upala u isti bucket u tom koraku nece promeniti redosled. Ovo svojstvo je veoma vazno. Kada zavrsimo prvi korak, nema potrebe da za svaku grupu ponavljamo algoritam (i time pravimo nove buckete), vec u svakom koraku primenjujemo isti algoritam na celi niz, samo pomeramo decimalno mesto (pocinje se od cifre najmanje tezine) - time se stedi dosta prostora. [ Sinalco @ 15.05.2005. 02:33 ] @
Svaka cast, Srki...
Jos samo treba upotrebiti odgovarajucu strukturu za odgovarajuci problem :-) [ Srđan Krstić @ 15.05.2005. 03:51 ] @
Grafovsi algoritmi (graph algorithms)
Teorija grafova je verovatno najkompleksnija oblast od ovih nekoliko koje navodim u ovoj temi. Zbog toga cu je podeliti u nekoliko poruka, i napraviti malo veci uvod. [Ovu poruku je menjao IsrkiboyI dana 18.05.2005. u 16:09 GMT+1] [ sklitzz @ 16.05.2005. 14:10 ] @
Daj molim te ako znaš neki sajt o Tournament tree strukturi pošalji koji link
[ Srđan Krstić @ 18.05.2005. 15:10 ] @
Definicije pojmova u teoriji grafova
Graf  predstavlja uredjeni skup predstavlja uredjeni skup 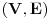 , gde je , gde je  skup cvorova (vertices), a skup cvorova (vertices), a  skup ivica (edges), u kome svaka ivica predstavlja par skup ivica (edges), u kome svaka ivica predstavlja par 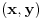 cvorova iz cvorova iz  . Kazemo da su dva cvora susedna (adjacent) ako i samo ako postoji ivica koja ih spaja, i takodje da je cvor . Kazemo da su dva cvora susedna (adjacent) ako i samo ako postoji ivica koja ih spaja, i takodje da je cvor  susedan (incident) ivici susedan (incident) ivici  ako i samo ako je ako i samo ako je  jedan od cvorova spojenih ivicom jedan od cvorova spojenih ivicom  . Broj ivica koje su susedne sa nekom cvorom je stepen (degree) tog cvora. Svi cvorovi koji su susedni nekom cvoru . Broj ivica koje su susedne sa nekom cvorom je stepen (degree) tog cvora. Svi cvorovi koji su susedni nekom cvoru  se nazivaju susedima (neighbors) se nazivaju susedima (neighbors)  . Skup svih suseda nekog cvora . Skup svih suseda nekog cvora  obelezava se sa obelezava se sa 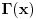 . Za neki podskup . Za neki podskup 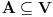 , definisemo , definisemo 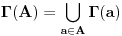 . Ivica koja spaja neki cvor . Ivica koja spaja neki cvor  sa samim sobom zove se petlja (loop). Prost graf je graf koji nema ni petlji ni visestrukih ivica, sto znaci da nijedna dva cvora nisu spojena sa vise od jednom ivicom. Graf moze biti neusmeren (undirected) ili usmeren (directed), kod koga svaka ivica ima i svoj smer (znaci ako je sa samim sobom zove se petlja (loop). Prost graf je graf koji nema ni petlji ni visestrukih ivica, sto znaci da nijedna dva cvora nisu spojena sa vise od jednom ivicom. Graf moze biti neusmeren (undirected) ili usmeren (directed), kod koga svaka ivica ima i svoj smer (znaci ako je  povezano sa povezano sa 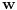 , ne mora biti i da je , ne mora biti i da je 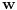 povezano sa povezano sa  ). Takodje, graf moze biti i tezinski (weighted) ako svaka ivica ima sebi dodeljenu neku vrednost (tezinu). I netezinski graf moze se posmatrati kao tezinski, s tim sto bi tezina svake ivice bila jednaka (recimo 1). Zato u daljem tekstu necu navoditi eksplicno da li je graf tezinski ili ne, ukoliko to nije od krucijalnog znacaja za sam algoritam.Put (path) od cvora ). Takodje, graf moze biti i tezinski (weighted) ako svaka ivica ima sebi dodeljenu neku vrednost (tezinu). I netezinski graf moze se posmatrati kao tezinski, s tim sto bi tezina svake ivice bila jednaka (recimo 1). Zato u daljem tekstu necu navoditi eksplicno da li je graf tezinski ili ne, ukoliko to nije od krucijalnog znacaja za sam algoritam.Put (path) od cvora  do nekog drugog cvora do nekog drugog cvora  je niz ivica koji spaja ova dva cvora, u kome se svaka ivica iz grafa pojavljuje najvise jedanput. Ako neki niz ivica spaja cvor je niz ivica koji spaja ova dva cvora, u kome se svaka ivica iz grafa pojavljuje najvise jedanput. Ako neki niz ivica spaja cvor  sa samim sobom, onda se takav niz zove krug (cycle). Drvo (tree) je graf koji nema krugova. Za graf kazemo da je povezan (connected) ako i samo ako za svaka dva njegova cvora postoji put koji ih spaja. Ako graf nije povezan, onda se on moze razbiti na povezane komponente (connected components), disjunktne po cvorovima. Bipartitan (bipartite) graf sa samim sobom, onda se takav niz zove krug (cycle). Drvo (tree) je graf koji nema krugova. Za graf kazemo da je povezan (connected) ako i samo ako za svaka dva njegova cvora postoji put koji ih spaja. Ako graf nije povezan, onda se on moze razbiti na povezane komponente (connected components), disjunktne po cvorovima. Bipartitan (bipartite) graf 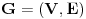 je graf u kome se mogu uociti dva disjunktna skupa cvorova, je graf u kome se mogu uociti dva disjunktna skupa cvorova, 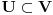 i i 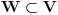 , tako da svaka ivica iz , tako da svaka ivica iz  spaja jedan cvor iz spaja jedan cvor iz  sa jednim cvorem iz sa jednim cvorem iz 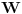 . Pokrivac ivica (vertex cover) grafa . Pokrivac ivica (vertex cover) grafa 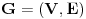 je skup je skup 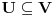 , takav da je svaka ivica iz , takav da je svaka ivica iz  susedna sa bar jednim cvorom iz susedna sa bar jednim cvorom iz  . Uparivanje (matching) u grafu . Uparivanje (matching) u grafu 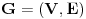 je skup je skup 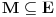 disjunktnih ivica, tj. ivica od kojih nikoje dve nemaju nijedan zajednicki cvor. Za svako uparivanje disjunktnih ivica, tj. ivica od kojih nikoje dve nemaju nijedan zajednicki cvor. Za svako uparivanje  postoji podskup cvorova postoji podskup cvorova 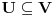 u kome je svaki cvor susedan tacno jednoj ivici iz u kome je svaki cvor susedan tacno jednoj ivici iz  . Za graf kazemo da je k-povezan akko izmedju svaka dva cvora postoji k puteva disjunktnih po ivicama. Specijalno, za 2-poveznan graf kazemo da je bipovezan. Usmeren graf je jako povezan akko za svaka dva cvora . Za graf kazemo da je k-povezan akko izmedju svaka dva cvora postoji k puteva disjunktnih po ivicama. Specijalno, za 2-poveznan graf kazemo da je bipovezan. Usmeren graf je jako povezan akko za svaka dva cvora  i i 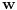 postoji put od postoji put od  do do 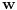 kax] do kax] do 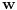 i od i od 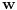 do do  . Ojlerov put (Eulerian tour) u grafu je put (ili krug) koji sadrzi svaku ivicu tacno jednom. Hamiltonov put (Hamiltonian tour) je put (ili krug) koji sadrzi svaki cvor tacno jednom. . Ojlerov put (Eulerian tour) u grafu je put (ili krug) koji sadrzi svaku ivicu tacno jednom. Hamiltonov put (Hamiltonian tour) je put (ili krug) koji sadrzi svaki cvor tacno jednom.[Ovu poruku je menjao Srđan Krstić dana 20.05.2005. u 18:21 GMT+1] [ Srđan Krstić @ 18.05.2005. 15:12 ] @
Oblilasci grafa
Obilazak grafa (graph traversal) je princip kojim treba obici svaku ivicu i svaki cvor nekog grafa. Ovo je izuzetno cesto potrebno uraditi, stavise deo skoro svakog slozenijeg algoritma je neki obilazak grafa. Ovde cu opisati 2 algoritma za obilazak: DFS DFS (Depth First Search) je obilazak grafa "u dubinu". Obelezimo sve cvorove da nisu prodjeni. Sada uzmemo neki cvor obelezimo ga kao prodjen, i skeniramo sve njegove susede. Za svakog koji nije prodjen, odmah pozovemo DFS rekurzivno. Jasno je odakle ime ovom algoritmu, jer on graf bukvalno prolazi "u dubinu". Ukoliko je ostao jos neki neobidjen cvor po zavrsetku rada algoritma, znaci da graf nije povezan. Ovo je ujedno i najlaksi moguci nacin za pronalazenje povezanih komponenti grafa. Pri oblisaku grafa, mozemo numerisati cvorove redom kojim ih obilazimo, cime dobijamo DFS numeraciju cvorova. Izuzetno jednostavan algoritam za implementiranje. Slozenost algoritma je 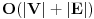 , jer svaki cvor i svaku ivicu razmatramo konstantan broj puta (cvor jednom a ivicu dvaput). , jer svaki cvor i svaku ivicu razmatramo konstantan broj puta (cvor jednom a ivicu dvaput).BFS BFS (Breadth First Search) je obilazak grafa "u sirinu". Za ovaj algoritam koristi se struktura podataka red (queue). Red je na pocetku prazan, a onda u njega ubacujemo jedan element. U svakoj iteraciji, uzimamo sledeci element sa reda, i, kao malopre, skeniramo sve njegove susede. Sve koji nisu obidjeni stavljamo na queue. Na ovaj nacin graf obilazimo "red po red", dakle prvo cvor od koga smo posli, pa sve njegove susede na prvom nivou, pa sve na drugom itd. Zato, kada prvi put obidjemo neki cvor v, nivo na kome smo ga obisli je ujedno i najkraci put od polaznog cvora do cvora v (ukoliko graf nije tezinski). Kao i malopre, ukoliko graf nije povezan treba pustiti BFS iz nekog cvora svake komponente. Slozenost algoritma je ista kao i DFS-a, 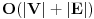 . .Vidimo da su oba algoritma iste slozenosti. Iz mog iskustva (ne garantujem za istinitost podataka koje cu upravo da iznesem), u C-u DFS radi nesto brze nego BFS, za razliku od Pascal-a, gde je obrnuto. Naravno, ovo umnogome zavisi i od tipa grafa, i od optimizacija samog kompajlera i od jos trista cudesa, ali moje testiranje je pokazalo podatke koje sam rekao. Razlika je inace mala, cinjenica je da su algoritmi iste slozenosti, ali ipak osetna. Animacija rada dfs i bfs algoritama http://www.ics.uci.edu/~eppstein/161/960215.html Topolosko sortiranje Topolosko sotiranje predstavlja numerisanje svih cvorova nekog usmerenog grafa, tako ako se iz v moze doci u w, broj dodeljen cvoru v je manji od broja dodeljenog w. Primetimo da validno topolosko sortiranje postoji samo u drvetu. Prirodno je dodeljivati vrednosti od 1 do |V|. Ideja je sledeca: nadju se indegree-ovi svih cvorova (npr. DFS-om). Uzmemo one kojima je indegree 0, i stavimo ih na queue. Sa queue uvek uzimamo prvi cvor, numerisemo counterom (koji pocinje od 0, i povecava cim se nekom cvoru dodeli). Kad numerisemo neki cvor, izbacimo ivice koje iz njega polaze, i naravno updateujemo indegree za cvorove sa kojima su bili spojeni. Cim nekom cvoru indegree postane 0, dodajemo ga na queue. Slozenost - 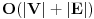 . .http://www.geocities.com/Silic...ey/Garage/3323/aat/a_topo.html http://www.cs.auckland.ac.nz/~...ml#SECTION00042000000000000000 Floyd-Warshall Floyd-Warshall-ov algoritam je izuzetno jednostavan algoritam koji nalazi najkrace puteve izmedju svaka dva cvora u grafu. On radi dinamicki: povecava graf ubacujuci u svakoj iteraciji po jedan novi cvor, k, i u svakoj iteraciji za svaka dva cvora proverava da li je krace ici od jednog do drugog preko k. Treba dobro obratiti paznju na redosled petlji, jer nije svejedno! Petlje treba da idu redom k, i, j, a glavni red treba da izgleda otprilike ako je put [i, j] duzi od put [i, k] + put [k, j], promeni put [i, j]. Slozenost je, ocigledno, 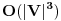 http://www.algorithmist.com/index.php/Floyd-Warshall's_Algorithm http://www.cs.ucf.edu/~reinhard/classes/cop3503-fall03/floyd.pdf Dijkstra Dijskstrin algoritam sluzi za nalazenje najkracih puteva od nekog cvora v do svih ostalih cvorova u grafu. Radi tako sto za svaki cvor x pamti sp [x], sto predstavlja trenutno najkraci put od v do x. Na pocetku obelezimo v kao prodjen. U svakoj iteraciji, trazi se cvor x koji ima najmanji sp a da nije prodjen. Njega obelezimo kao prodjen, i proverimo za sve njegove susede w, da li je sp [x] + edge [x, w] < sp [w], pa ako jeste, updateujemo sp [w]. Za implementaciju ovog algoritma za sp bi pozeljno bilo koristiti heap, jer nam u svakom trenutku treba najmanja vrednost sp. Sa heapom, slozenost algoritma je 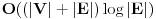 . Ukoliko se ne koristi heap, vec obican niz, slozenost je . Ukoliko se ne koristi heap, vec obican niz, slozenost je 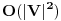 . .Aplet koji prikazuje rad Dijkstrinog algoritma http://www.cs.usask.ca/resourc...dvanced/dijkstra/dijkstra.html Minimalno drvo razapinjanja Minimalno drvo razapinjanja (minimum cost spanning tree (MCST)) u grafu 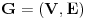 je njegov podgraf je njegov podgraf 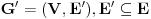 , koji je drvo, i uz to zbir tezina ivica u , koji je drvo, i uz to zbir tezina ivica u 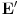 ima najmanju mogucu vrednost. Navodim dva poznatija algoritma za nalazenje MCST: ima najmanju mogucu vrednost. Navodim dva poznatija algoritma za nalazenje MCST:Primov algoritam Primov algoritam je u sustini samo modifikacija Dijkstre. Algoritmi su skoro identicni, pa cu samo navesti razliku, a to je da se u sp nizu ne cuva najkraca vrednost puta do polaznog cvora, vec do drveta (tj. do bilo kog cvora u drvetu). Znaci razlika je sto proveravamo samo da li je edge [x, w] < sp [w], i ako jeste, updateujemo sp [w]. Slozenost je naravno ista kao i kod Dijkstre. lep aplet koji pokazuje rad primovog algoritma http://www.personal.kent.edu/~...ithms/GraphAlgor/primAlgor.htm Kruškalov algoritam Kruskalov algoritam je drugi poznat algoritam za nalazenje MCST u grafu. Radi koristeci teoremu da je u msct-u minimizirana najduza ivica. Sada je problem trivijalan: sortiramo ivice rastuce, i ubacujemo jednu po jednu redom. Ukoliko su dva cvora koje spaja neka ivica vec povezana (postoji neki put izmedju njih), preskacemo tu ivicu, ako ne, dodajemo je u mcst, sve dok graf ne bude povezan. Ovde je korisno koristiti union-find strukturu podataka, jer kada spojimo neka dva cvora koja dotad nisu bila spojena, treba nekako naglasiti da oni sad cine istu komponentu grafa, sto se lako radi nalazenjem unije komponenti ta dva cvora. Ako tako radimo, slozenost glavnog dela je 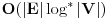 , ali je ukupna slozenost , ali je ukupna slozenost 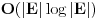 , zbog sortiranja ivica. , zbog sortiranja ivica.lep aplet koji pokazuje rad kruskalovog algoritma http://www.personal.kent.edu/~...ms/GraphAlgor/kruskalAlgor.htm Ojlerov put (Eulerian Tour) Vec je opisano u prethodnom postu sta je Ojlerov put u grafu. Postoji teorema koja kaze da ojlerov put postoji akko graf ima tacno 0 ili 2 cvora sa neparnim stepenom. Dokaz je trivijalan: u svaki cvor moramo "uci" jednom ivicom, a "izaci" drugom, pa, osim prvog i zadnjeg cvora na putu, svi moraju imati paran stepen. Ukoliko svi cvorovi imaju paran stepen, mozemo poci iz bilo kog cvora i zavrsiti u bilo kom cvoru, i taj Ojlerov put je zapravo ciklus. Prvo treba pronaci stepene svih cvorova, pa videti prvo da li uopste postoji Ojlerov put, a ako postoji, odakle treba poceti sa trazenjem puta (od nekog cvora sa neparnim stepenom ako ih je 2, ili od bilo kog ako su svi parnog stepena)). citiram vrlo jednostavno objasnjenje algoritma sa usaco sajta: Citat: The basic idea of the algorithm is to start at some node the graph and determine a circuit back to that same node. Now, as the circuit is added (in reverse order, as it turns out), the algorithm ensures that all the edges of all the nodes along that path have been used. If there is some node along that path which has an edge that has not been used, then the algorithm finds a circuit starting at that node which uses that edge and splices this new circuit into the current one. This continues until all the edges of every node in the original circuit have been used, which, since the graph is connected, implies that all the edges have been used, so the the resulting circuit is Eulerian. More formally, to determine a Eulerian circuit of a graph which has one, pick a starting node and recurse on it. At each recursive step: Pick a starting node and recurse on that node. At each step: If the node has no neighbors, then append the node to the circuit and return If the node has a neighbor, then make a list of the neighbors and process them (which includes deleting them from the list of nodes on which to work) until the node has no more neighbors To process a node, delete the edge between the current node and its neighbor, recurse on the neighbor, and postpend the current node to the circuit. A evo i pseudokoda: Code: Input: G = (V, E) (graf) v (pocetni cvor) Output: tour (Eulerian Tour) Procedure findcircuit (v) if v has no neighbours add v to tour else while v has neighbours pick an edge (v, w) remove edges (v, w) and (w, v) findcircuit (w) add v to tour [Ovu poruku je menjao IsrkiboyI dana 18.05.2005. u 16:22 GMT+1] [ Srđan Krstić @ 18.05.2005. 15:14 ] @
Jako povezane komponente
Jako povezana komponenta usmerenog grafa je njegov podgraf takav da se u okviru njega iz svakog cvora moze stici u svaki drugi. Svaki usmereni graf moze se “razbiti” na jako povezane komponente. Treba imati na umu sledecu cinjenicu: Dva cvora pripadaju istoj jako povezanoj komponenti ako i samo ako posoji ciklus koji ih obe sadrzi. Graf obilazimo DFS-om. Usput cvoreve numerisemo opadajucim DFS brojevima. Ako iz nekog cvora mozemo doci u neki ciji je DFS broj veci, onda je ta ivica sigurno ili back ili cross edge. Sada definisemo high vrednost za svaki cvor kao najveci DFS broj do koga se moze stici iz njega ili njegovih potomaka. Inicijalno je high vrednost nekog cvora jednaka njegovom DFS broju. Neka razmatramo cvor v. Ukoliko postoji back edge iz nekog od njegovih potomaka koja ide “vise” od v, onda je jasno da postoji ciklus koji sadrzi v, pomenutog potomka i taj cvor visi od v, pa podgraf od v “nadole” nije jako povezana komponenta. Ako pak od v-ovog potomka w naidjemo na cross edge w-x, onda znaci da x ne pripada ni jednoj do sad pronadjenoj komponenti, jer kada odredimo da neki cvor pripada nekoj komponenti, vise ga ne razmatramo. Dakle, moze se ici “vise” od x, pa v ne moze biti “root” jako povezane komponente, jer v, zajedno sa w, x, i zajednickim pretkom x i v cini ciklus. Dakle, ako u prolasku grafa od cvora v “nadole” ne naidjemo ni na back ni na cross edge, tj. high cvora v ostane jednaka njegovom DFS broju, onda znamo da podgraf ciji je root v cini jako povezanu komponentu, pa je mozemo obeleziti i nastaviti obilazak bez nje. Na pocetku inicijalizujemo _dfsn na n (n je broj cvorova), cur_comp na 0, dfsn i comp vrednosti svih cvorova takodje na 0, i pozivamo scc (v) dokle god postoji cvor v koji je neobidjen, tj. dfsn [v] = 0. Slozenost je dakle jednaka slozenost DFS-a, 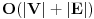 . Radi lakseg razumevanja, navodim i pseudokod: . Radi lakseg razumevanja, navodim i pseudokod:Code: Procedure scc (v) dfsn [v] = _dfsn _dfsn = _dfsn – 1 push v into stack high [v] = dfsn [v] for all edges (v, w) if dfsn [w] = 0 scc (w) if high [w] > high [v] high [v] = high [w] else if (dfsn [w] > dfsn [v]) and (comp [w] = 0) if dfsn [w] > high [v] high [v] = dfsn [w] if high [v] = dfsn [v] cur_comp = cur_comp + 1 repeat remove x from stack comp [x] = cur_comp until x = v http://www.ececs.uc.edu/~gpurdy/lec25.html http://www-2.cs.cmu.edu/afs/an...15/354/www/postscript/sccs.pdf Uparivanja Uparivanje je moja omiljena tema u ovoj oblasti. Zato necu da pisem nista ukratko, nego sam uz poruku uploadovao rad koji sam pisao na temu uparivanja. Rad sam prvobitno pisao na engleskom jeziku, sto sam i uploadaovao u attachment, ali sam ga kasnije preveo i na srpski jezik, pa ako nekog interesuje ta verzija, neka mi se obrati na pp (mogo bi neko i da proof-readuje tu srpsku verziju, jer sam ga prevodio dosta brzo i ofrlje, sto se nije odrazilo na smisao, ali ima recimo puno stamparskih gresaka i slicno (mrzelo me da se vracam par karaktera unazad i kad vidim da sam pogresio :))). Takodje, sto se tice literature o ovoj temi, kao i za sve ostalo moze se dosta toga naci na netu, ali ipak mnogo manje nego za neke druge teme. Ja imam dosta radova i knjiga na tu temu na mom kompu, pa i za to moze da mi se obratite na pp (ako bude vece interesovanje, uploadovacu negde i linkovati ovde). Protok (Network Flow) Zadat je tezinski usmereni graf, gde duzine ivica predstavljaju njihove kapacitete i postoje dva karakteristicna cvora (source i sink), takvi da su indegree source-a i outdegree sink-a 0. Treba naci kolika maksimalna kolicina moze “proteci” kroz graf, od source-a do sink-a, tako da kroz svaku ivicu ne moze proteci vise od njenog kapaciteta, i za svaki cvor (osim source-a i sink-a) je ulazni protok jednak izlaznom. U svakom prolasku kroz graf nalazimo put od source-a do sink-a, i to najbolje put sa najvecim kapacitetom (pathcacacity). Za nalazenje takvog puta koristimo modifikaciju Dijkstrinog algoritma. Sada kapacitet svake ivice na tom putu umanjujemo za pathcapacity i pored toga dodamo jos jednu ivicu izmedju ista dva cvora, ali u suprotnom smeru, i zadamo joj kapacitet pathcapacity. Ukoliko ova ivica vec postoji, jednostavno joj uvecamo kapacitet za pathcapacity. Zavrsavamo kada vise nema puteva kapaciteta razlicitog od nule. Ovaj algoritam moze se koristiti i za nalazenje maximum matching-a u bipartitnom grafu, i to tako sto svakoj ivici zadamo tezinu 1, napravimo source koji spojimo sa svim cvorovima na jednoj strani grafa, i napravimo sink koji spojimo sa svim cvorovima iz drugog dela grafa, tako da sve nove ivice imaju tezinu 1. MinCut je skup ivica najmanje ukupne tezine koje treba iseci da graf vise ne bi bio povezan. Taj zbir tezina jednak je maksimalnom protoku kroz graf (cuvena max flow - min cut teorema). Da bi odredili koje su to ivice koje treba iseci, pustimo, recimo, DFS od source-a i obelezimo sve cvorove do kojih smo stigli. Sve ivice koje spajaju obidjeni i neobidjeni cvor su deo MinCut-a. Ako treba naci MinCut sa najmanjim brojem ivica, pre pustanja flow-a treba pomnoziti tezinu svake ivice sa m + 1 (m je broj ivica u grafu) i dodati 1. Tada je pravi flow jednak dobijenom flow-u po modulu m + 1. Slozenost je O (MaxFlow * m), jer u svakoj iteraciji povecavamo MaxFlow bar za 1, ali generalno algoritam radi dosta brze, jer se obicno MaxFlow povecava za vise od 1. Opisani algoritam (Ford-Fulkerson) radi samo ako su kapaciteti ivica celi brojevi. Flow je, po meni, kao i matching, izuzetno interesantna (a i siroka) tema, pa planiram da ovom problemu posvetim i posebnu temu. Tada cu je linkovati ovde. Za literaturu mi se kao i za matching obratite na pp bar za sad, jer cu verovatno dosta toga da prikacim uz temu koja bude posvecena samo ovom problemu. Za sad, evo pseudokoda: Code: Input: G = (V, E) (graf) source, sink Output: MaxFlow (maksimalni protok) Procedure Flow MaxFlow = 0 while (1) for all vertices i prevnode [i] = -1 flow [i] = 0 visited [i] = 0 flow [source] = infinity while (1) max = 0 maxi = -1 for all vertices i if flow [i] > max and not visited [i] max = flow [i] maxi = i if maxi = -1 break if maxi = sink break visited [maxi] = 1 for all neighbours i of maxi if flow [i] < min(max, cap [maxi, i]) flow [i] = min(max, cap [maxi, i]) prevnode [i] = maxi if maxi = -1 break pathcapacity = flow [sink] MaxFlow = MaxFlow + pathcapacity curnode = sink while curnode <> source nextnode = prevnode [curnode] cap [nextnode, curnode] -= pathcapacity cap [curnode, nextnode] += pathcapacity curnode = nextnode [ Srđan Krstić @ 18.05.2005. 15:19 ] @
Citat: sklitzz: Daj molim te ako znaš neki sajt o Tournament tree strukturi pošalji koji link Ummmm, nisam nikad cuo za "tournament tree". Progooglao sam malo, bas mi i ne deluje kao neka struktura koja se koristi u programiranju... Ajde objasni malo sta je to [ Srđan Krstić @ 18.05.2005. 15:36 ] @
Upcoming:
Geometrijski algoritmi Heuristike i NP problemi Ostali problemi, koje nisam mogao da svrstam u navedene kategorije [ sklitzz @ 19.05.2005. 17:58 ] @
To ti je neka vrsta BST-a koliko ja znam, nisam siguran ali mislim da je to i nešto novijeg datuma. Tournament tree bi trebalo simulirati utakmice(turnir). Nezam točno kako zato sam i pitao ako znaš koji sajt jer ja isto ništa nisam našao...
 [ anon315 @ 20.05.2005. 11:11 ] @
E pa super, ajmo onda da resimo jedan praktican problemcic umesto samo da teoretisemo.
U pitanju je binarno stablo i preorder, inorder i postorder obilazak. Ovo nije problem. Medjutim, javio mi se zadacic gde imam inorder i preorder poredak, a na osnovu toga treba nacrtati izgled drveta. Kako se resava ovaj (inverzni) problem? Kako da krenem, sta da gledam itd.? Evo primera: preorder: ATNEIFCSBDGPMLK inorder: EINSCFBTGPDLMKA [ anon315 @ 20.05.2005. 12:45 ] @
Srki majstore, ovo mi je upravo trebalo!
 Hvala [ Gojko Vujovic @ 20.05.2005. 17:00 ] @
Bravo Srki za ovo gore! Bilo bi dobro da za dodatne probleme i rešenja pravite nove teme, da ne mešamo to sa ovim tutorialima. Dakle ovo postavi kao novu temu pa će Srki prebaciti odgovor :)
[ frane22 @ 29.08.2005. 20:23 ] @
Trebam napraviti seminarski o Maximum flow problemu, nemam pojma šta je to čemu služi, niti želim znat, samo želim seminar. ima li itko išta materijala, bio bi zahvalan...
[ Der Forscher @ 20.01.2006. 12:46 ] @
Kao Prvo.. Sajt e fenomenalan..
Ako moze da mi posaljete link, za download na pdf.. Algorithms and Data Structures in Java.. Hvala puno [ Srđan Krstić @ 20.01.2006. 16:38 ] @
Ne znam za tu knjigu, ali ovo ti je verovatno pandan (Robert Sedgewick - Algorithms in Java):
Parts 1-4: http://proquest.safaribooksonline.com/0201361205 Part 5: http://proquest.safaribooksonline.com/0201361213 Nazalost, nije pdf, nego je u html-u okacena na sajt, ali mozes da skines sve stranice pa da je citas offline [ Kvasac @ 28.01.2006. 17:12 ] @
Molit cu bilo koga da se javi i posta bilo kakav link ili nesto o izracunavanju slozenosti algoritama. Hvala unaprijed
[ NrmMyth @ 29.01.2006. 10:43 ] @
Par pitanja.
Je li AVL drvo, RB drvo ( red-black tree )? Dali Bucket Sort, hashira brojeve u tablicu i onda prolazom izbacujemo brojeve sortirane. [ bugojanac @ 13.05.2006. 22:35 ] @
Pozdrav, da li neko ima kod za heap (sekvancijalna reprezentacija) u C++, mozda je neko vec postavio ali nemam vremena gledati sve,
Hvala unaprijed [ toroman @ 01.08.2006. 22:08 ] @
Bez ljutnje, da li se slažete da je potrebno obrisati ova pitanja?
Mislim da temu treba očistiti. Stvarno je odlična a pitanja je samo kvare, ionako niko ne odgovara na njih ... Mislim uredu je da neko postavi pitanje, pa mu neko odgovori i onda se obriše pitanje ... Ali neka samo stoje i smetaju. [ Zeroo @ 28.11.2006. 22:47 ] @
E da nema šta o Caching algoritmima...least frequently used (LFU), least recently used (LRU), most recently used (MRU), first in first out (FIFO),Random...tražio sam pseudokod na netu al ga nisam nasao...pa ak neko zna neš neka otipka..tnx
[ mknezevic @ 02.05.2007. 12:46 ] @
Dobar dan!!
Pozdrav za sve korisnike ovog foruma.. Zelio bih da zamolim nekoga ko zna o TEORIJI GRAFOVA i programiranje U C# da mi pokaze kod ili da mi da adresu dje bih mogao naci CODE za PRESJEK DVA GRAFA... Nikako da nadjem to, ni u GOOGLE ni nidje... Ako neko moze da mi pomogne bio bih veoma zahvalan!! pozdrav jos jendom [ ivan.mile @ 02.05.2007. 13:50 ] @
Citat: mknezevic: Dobar dan!! Pozdrav za sve korisnike ovog foruma.. Zelio bih da zamolim nekoga ko zna o TEORIJI GRAFOVA i programiranje U C# da mi pokaze kod ili da mi da adresu dje bih mogao naci CODE za PRESJEK DVA GRAFA... Nikako da nadjem to, ni u GOOGLE ni nidje... Prvo moraš da definišeš šta je presek dva grafa. Po definiciji, graf je uređeni par (X, p) gde je X neprazni skup čiji su elementi čvorovi grafa, a p je binarna relacija u skupu X; elementi relacije p su grane grafa. Što se tiče operacija nad 2 grafa, znam da postoje: unija, potpuni proizvod, proizvod i suma. Ne znam da li postoji presek 2 grafa. [ osmania @ 30.01.2008. 20:42 ] @
Ne znam da li sam na pravoj adresi ali zelim da pitam da li imate algoritam (code + teorija)
od double hashing with quicksort. Hvala puno [ maricn @ 13.05.2008. 16:07 ] @
Odredjivanje artikulacionih tacaka (kao dopuna definicijama pojmova u teoriji grafova)
U datom povezanom grafu G = (V,E), cvor u predstavlja artikulacionu tacku ako brisanjem tog cvora i svih ivica koje polaze od tog cvora graf postaje nepovezan. Funkciju za odredjivanje artikulacionih tacaka mozemo dobiti modifikacijama na funkciji za obilazak grafa u dubinu. Neka je Ga = (V, Ea) drvo dobijeno od grafa G obilaskom u dubinu. Tada je: 1. Koren drveta Ga artikulaciona tacka ako ima barem dva naslednika (odnosno povezan je sa dva cvora u drvetu Ga); 2. Ako je v cvor koji nije koren drveta Ga onda je v artikulaciona tacka akko ne postoji povratna ivica (u,w) takva da je u naslednik cvora v, a w prethodnik cvora v u drvetu Ga. Ovo se moze iskoristiti da se odrede artikulacione tacke. Neka je: l[v] = min( {d[v]} U {d[w]}); ...gde je (u,w) povratna ivica i cvor u je naslednik cvora v; d[v] je niz veza cvora v (predstavljen nulama i jedinicama). Cvor v je artikulaciona tacka akko postoji njegov direktni naslednik u takav da je l[ u ] >= d[v]. Tako dobijamo funkciju za odredjivanje artikulacionih tacaka... http://cgm.cs.mcgill.ca/~msude.../articulation/articulation.pdf http://www.student.cs.uwaterlo...ourses/W03/section1/Unit17.pdf [Ovu poruku je menjao maricn dana 13.05.2008. u 17:18 GMT+1] [ Marko Nešić @ 08.01.2009. 20:51 ] @
Ja bih isto pitao neshto vezano za temu Matching-a (uparivanja) u grafovima! Ima li neko ko bi mogao pomoci ili ako znate lichni mail Srdjana Krstica?
Potreban mi je prevod njegovog attachmenta za tu temu i neki korisni linkovi na srpskom, a isto tako trebam uraditi i neki konkretan primer u flashu vezan za tu temu.. Trebao bih sastaviti seminarski od nekih 20-tak stranica, a nisam u toku, poshto mi je struka programiranje pre svega! Hvala unapred ;) [ boyan3001 @ 02.06.2013. 17:04 ] @
Da li neko moze da mi preporuci knjigu koja se bavi osnovnim algoritmima? Nesto sto bi moglo da se nazove programerskom azbukom. Knjiga koja bi predstavila i objasnila principe rada opstih, najcesce koriscenih i potrebnih algoritama bez kojih bi bilo nemoguce napisati bilo kakav slozeniji program. Otrpilike ono sto je u ovoj temi i popisano, ali objedinjeno u jednu knjigu. Ne trazim nuzno nesto sto je moguce nabaviti kod nas.
Nesto poput ovoga: http://en.wikipedia.org/wiki/The_Art_of_Computer_Programming [ Nedeljko @ 02.06.2013. 18:32 ] @
Slaviša B. Prešić - Algoritmika. On je pokojni profesor Matematičkog fakulteta u Beogradu, pa se raspitaj na fakultetu i Matematičkom institutu SANU oko toga gde može da se kupi. Štampali su je Rusi na ruskom, a ako nema gde da se nađe, a iz Beograda si, imam primerak koji bi mogao da se iskopira. Pored drugih kvaliteta, pisana je vrlo jasnim jezikom, tj. pitka je za čitanje.
Miodrag Živković, redovni profesor istog fakulteta je napisao knjigu "algoritmi", koju možeš da kupiš u skriptarnici fakulteta ili skineš sa njegove prezentacije na fakultetu http://poincare.matf.bg.ac.rs/~ezivkovm/ Vidi pod "algoritmi i strukture podataka". [ boyan3001 @ 03.06.2013. 13:37 ] @
Odlicno, hvala!
Ovu knjigu od profesora Zivkovica sam pregledao, to je manje vise to. Solidno je obimna i detaljna rekao bih i svasta pokriva. Posluzice za sada svakako. A za Presicevu cu proveriti da li i gde se moze naci. Ako sam te dobro shvatio, ti na prvom mestu preporucujes "Algoritmiku", kao bolje napisanu knjigu? Inace, ni strana literatura nije na odmet, as long as it is written in English. :) Da li neko ima ovu "The Art of Computer Programming", kakva je? [ Nedeljko @ 04.06.2013. 13:05 ] @
Citat: boyan3001: Ako sam te dobro shvatio, ti na prvom mestu preporucujes "Algoritmiku", kao bolje napisanu knjigu? Dobro si me shvatio. Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|