Da li je ovde 2x osnova logaritma ili ulazi u proizvod? Ako ulazi u proizvod koja je osnova, 10?

U prvom slucaju svodi se na ekvivalenta sistem:
0 < 2x,
0 < x^2 + 1 < 2x
<=> x > 0
x^2 + 1 < 2x
dalje lako...

A u drugom slucaju:
0 < 2x(x^2 + 1) < 10
<=> x > 0,
x^3 + x < 5
dalje lako...



...da je P deljiv sa Q, verovatno se to trazi?

Moze da se odmah podeli i uz malo racuna istera do kraja.

Drugi nacin je da primetis da su nule trinoma Q(x) brojevi w i w^2, gde je w treci koren iz jedinice razlicit od 1 [Q(x) = (x^3 - 1) / (x - 1)].

Lako se dobija:
P(w) = w^1996 + w^1001 + 1 = (w^3)^599*w + (w^3)^333*w^2 + 1 =
= w + w^2 + 1 = 0 [zato sto je w^3 = 1]
i P(w^2) = ... na isti nacin ... = 0

Znaci da je Q(x) = (x - w)(x - w^2) i P(x) = (x - w)(x - w^2)*R(x), pa je ocigledno da je P deljiv sa Q.

A za drugi zadatak mozes i da nadjes nule Q, a to su
Sada probamo da li su ove nule i nule polinoma P, sto radimo koristeci Moivreovu formulu:
.

Nema potrebe da se komplikuje, ovako ces samo na tezi nacin dokazati da je w^1996 = w i w^1001 = w^2.

1.

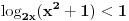
Ovaj zadatak se često nalazi u pripremama za prijemni, te pretpostavljam da tako glasi tvoj zadatak. Te ću ti uraditi baš gorenavedeni.

Prvo uslovi.


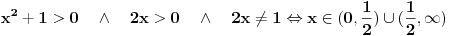
Dalje log mi predstavlja dekadni logaritam.



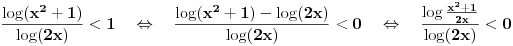
Sad rešimo

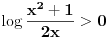
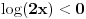
i tj
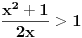
i
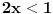
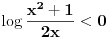
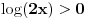
kao i i tj
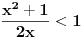
i
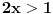
uz uslov
.

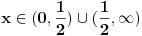
Pošto je x>0, u prvim nejednačinama se možemo osloboditi razlomaka.

Vidimo da nikad nije x²+1<2x, te ostaje samo prvi par nejednačina.




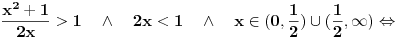
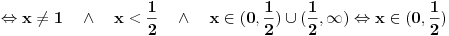
2.
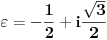
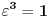
Ukoliko obeležimo vidimo da je , pa je
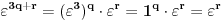
Dakle, kod stepena , nije potrebno da znamo sam stepen, nego njego ostatak pri deljenju sa 3.

Tada, pošto je ostatak pri deljenju 1996 sa 3 jednak 1 (1+9+9+6=25, 2+5=7, ostatak pri deljenju 7 sa 3 je 1) , vidimo da je

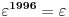
Takođe pošto je ostatak pri deljenju 1001 sa 3 jednak 1 (1+0+0+1=2), vidimo da je


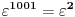
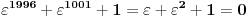
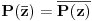
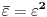
Dakle , zato što je nula polinoma Q. Pošto je za polinome sa realnim koeficijentima i vidimo da je


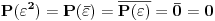
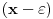
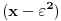
Dakle P je deljiv sa i sa , pa je deljiv i sa njihovim NZS-om, koji je u stvari proizvod, a to je baš Q(x)

hvala svima puno....... shta bi ja bez vas i vasih saveta....

pogodio si zadatak i jeste iz zbirke za prijemni....... i to iz FON-ove zbirke za pripremu prijemnog

@KPYU
e ne razumem zasto se kod 1 zadatka na kraju odbacuje resenje (1/2, beskonačno)

Dakle u drugom slučaju, mora da se desi


Ali


Vidimo da kvadrat realnog broja mora biti negativan, a to je nemoguće.