|
|
[ KPYU @ 16.05.2005. 00:33 ] @
H-ovi NE MORAJU biti izomorfni 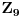 , već mogu biti izomorfni i 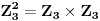
Što se preseka 2 različite grupe reda 9 tiče, može biti trivijalan ili reda 3, što će reći izomorfan 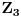 [ milicas @ 16.05.2005. 15:20 ] @
Ali G ima el. p reda 9 neka je on u 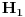
Neka je 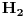 izomorfna 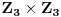
Vazi da su Silovljeve podgrupe istog reda medjusobno konjugovane, tj:
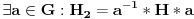
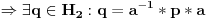
A inace vazi da je 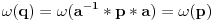
Dakle red od q je devet sto je nemoguce
 sve su izomorfne 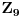
Mozda gresim?
Konkretno u ovom zadatku mogu samo da se prebroje elementi iz K-ova i L-ova, i dobije se tacno red G, ali negde je bas potrebno naci presek nekoliko podgrupa izomorfnih sa 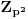 gde je p prost [ KPYU @ 17.05.2005. 15:51 ] @
Pogledaj grupu 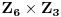 njen red je 18. Deder nađi mi neku njenu podgrupu izomorfnu sa 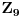
Ako imaš jednu, sve su takve. Ako nemaš ni jednu ...
U svakom slučaju, presek 2 različite grupe reda p n (p-prost broj) je grupa reda p k gde je 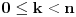 [ Cabo @ 18.05.2005. 15:07 ] @
Citat: milicas: Ali G ima el. p reda 9 neka je on u 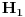
Neka je 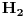 izomorfna 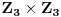
Vazi da su Silovljeve podgrupe istog reda medjusobno konjugovane, tj:
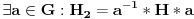
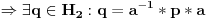
A inace vazi da je 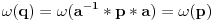
Dakle red od q je devet sto je nemoguce
 sve su izomorfne 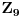
Mozda gresim?  ima element reda 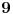 .
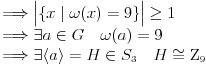
To znači samo da postoji jedna grupa izomorfna 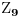 , a ne da su sve takve. [ milicas @ 18.05.2005. 17:57 ] @
Videla sam u ovogodisnjim vezbama iz algebre 1 da su bas za ovaj zadatak sve reda 9 ciklicne, ali nazalost, nema dokaza (ovaj odavde je moj). Jbg, valjda oni znaju bolje
[ Cabo @ 18.05.2005. 18:44 ] @
Možda su u pravu, a možda i nisu (nema dokaza).
Evo kako bih ja uradio ovaj zadatak:
Pretpostavimo da  nije prosta, pa 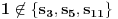 . Biće:
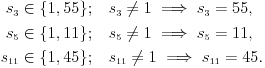
Sada imamo dve mogućnosti:
1)

Tada je
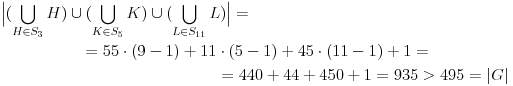
(kontradikcija).
2)

Tada je
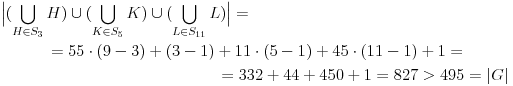
(kontradikcija). Ovde je  zato što se svake dve 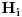 , 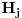 seku po  elementa, od kojih odbacujemo neutral, koji je sadržan u svim 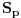 -podgrupama grupe  . Njega, kao i u slučaju 1), dodajemo na kraju.
Zaključak: mora biti 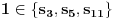 .
E, sad, ono što meni ovde „bode oči“ jeste to da uopšte nisam iskoristio podatak da postoji 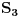 -podgrupa izomorfna 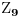 . Da li se u tom zadatku još nešto traži?
[ KPYU @ 19.05.2005. 00:21 ] @
@milicas
Ne znam što toliko insistiraš na nečemu što nije tačno, a uz to nigde ni ne koristiš.
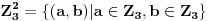 je grupa koja, evidentno, nije ciklična.
@ Cabo
Mada sam zahrđao pomalo, zar ne bi iz konjugovanosti podgrupa trebalo da sledi da su sve ciklične, ako je makar jedna ciklična. (Moguće da lupam)
Takođe, u dokazu si koristio kao činjenicu da se svih 55 podgrupa reda 9 seče po istoj podgrupi reda 3. To tako baš i nije. Treba izračunati broj podgrupa reda 3 (to nisu Silovljeve podgrupe), pa odatle računati. Najzad, ako u b) imaš više elemenata no što možeš, onda pod a) svakako imaš još više elemenata, tako da pod a) nisi ni trebao da računaš. [ Cabo @ 19.05.2005. 18:50 ] @
Citat: KPYU: Mada sam zahrđao pomalo, zar ne bi iz konjugovanosti podgrupa trebalo da sledi da su sve ciklične, ako je makar jedna ciklična. (Moguće da lupam)
Možeš li ovo malo da elaboriraš?
Citat: KPYU:
Takođe, u dokazu si koristio kao činjenicu da se svih 55 podgrupa reda 9 seče po istoj podgrupi reda 3. To tako baš i nije. Treba izračunati broj podgrupa reda 3 (to nisu Silovljeve podgrupe), pa odatle računati. Najzad, ako u b) imaš više elemenata no što možeš, onda pod a) svakako imaš još više elemenata, tako da pod a) nisi ni trebao da računaš.
Kako izračunati broj podgrupa reda 3?
Naravno da je suštinski ispitivanje slučaja 1) nepotrebno, ali zato na ispitu (bar na MATF-u) jeste potrebno sve to ispisati... analogno tome, ukoliko je ovaj ekstremni slučaj kada se sve 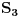 -podgrupe seku po podgrupi reda 3 (ova formula ne govori da je to ista podgrupa, već samo da svi preseci imaju po 3 elementa) kontradiktoran, zar onda nisu i ostali „prelazni“ slučajevi kontradiktorni? [ KPYU @ 20.05.2005. 05:47 ] @
Redom
1. Sve Silovljeve podgrupe su konjugovane.
2. Ako je b konjugat od a tada 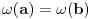
3. Ako je H 1 generisana elementom a i  , tada je 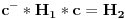 generisana elementom b
Dakle ako je H 1 ciklična, to je i svaka njoj konjugovana grupa, a to su sve grupe istog reda
Dalje postoji Silovljeva teorema koja nam, za datu grupu reda n 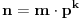 gde p-prost i 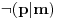 govori broj podgrupa reda p r ( 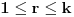 ).
Najzad, na algebri I ima pametnih ljudi (bar ih je bilo dok sam ja studirao), mada ne znam ko je tebi bio asistent. Ti pametni ljudi će shvatiti kad napišeš "...a trivijalno se pokazuje da je ovo kud i kamo više nego u drugom slučaju"
PS Mada nije iz ove teme, vidim da si mi skrenuo pažnju na gramatičku grešku. Imam opravdanje: bio sam jako umoran dok sam pisao poruku.
[Ovu poruku je menjao KPYU dana 20.05.2005. u 13:16 GMT+1][ Nedeljko @ 20.05.2005. 09:49 ] @
Konjugacija podgrupa je istovremeno i njihov izomorfizam, dok je konjugacija u grupi automorfizam te grupe. Takvi automorfizmi grupe se još zovu unutrašnji. Ako je  grupa, i za 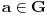 sa 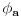 označimo unutrašnji automorfizam grupe  definisan sa 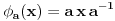 , onda skup 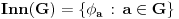 čini grupu odnosu na slaganje funkcija i pritom važi 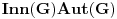 i 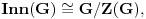 gde je 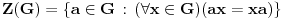 centar grupe 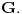 Centar grupe je uvek i njena normalna podgrupa, tako da je količpnička grupa 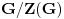 dobro definisana.
Zaključak, ako je jedna Silovljeva p-podgrupa grupe G ciklična, onda su i sve ostale Silovljeve p-podgrupe ciklične, budući da su sve one međusobno izomorfne kao konjugovane. [ Cabo @ 22.05.2005. 20:25 ] @
Citat: KPYU:
Dalje postoji Silovljeva teorema koja nam, za datu grupu reda n 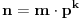 gde p-prost i 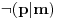 govori broj podgrupa reda p r ( 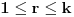 ).
Da, čitam sada teoriju i vidim da važi 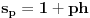 gde je 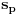 broj grupa reda 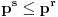 , a 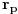 broj grupa reda 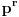 . U svesci iz koje sam vežbao se sa 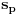 označava samo broj grupa reda 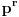 . Pa, kako onda, da li se 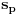 računa slično kao 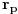 ? Dakle, 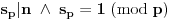 ? Kako se razlikuje računanje 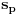 od računanja 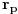 ?
Citat: KPYU:
Najzad, na algebri I ima pametnih ljudi (bar ih je bilo dok sam ja studirao), mada ne znam ko je tebi bio asistent. Ti pametni ljudi će shvatiti kad napišeš "...a trivijalno se pokazuje da je ovo kud i kamo više nego u drugom slučaju"
Dobro, ja sam samo poučen iskustvom sa Analize I (koga su zmije ujedale...  ).
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|