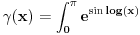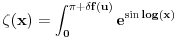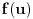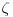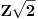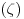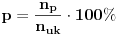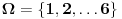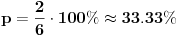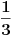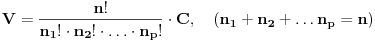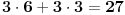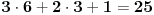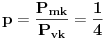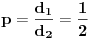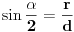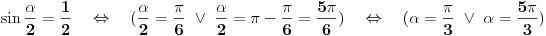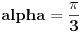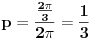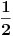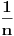Pa naravno da je 33.33% !

Sta sad, kolika je verovatnoca da ti ovog trenutka uleti slon kroz prozor? 50%, ili ce da uleti, ili ne.... J*ba ga....

dobro si rekao i pogodio sa slonovima da je šansa 50 % kao što je vjerojatnoca da ceš dobiti posaao u istom tom postotku , malo razmisli a ne bubaš kao maksim po diviziji ciao!
tata

Aha... Pa znaci tebi je kuca prepuna slonova, huh ?

Vidim da nisi sposoban razmisljati logicki i apstraktno u ovoj dilemi i nemoj se vise
molim te javljat!

Ne znam sto se bunis uopste! Lepo si pitao kolika je verovatnoca, i ja sam ti lepo odgovorio. To sto se ti ne slazes sa mnom nije razlog da se ponasas krajnje drsko i nevaspitano kako se ponasas. Trebalo bi da mi budes zahvalan sto sam izdvojio vremena da ti odgovorim na pitanje.

A hteo ti to ili ne, verovatnoca jeste 33.33%. Po tvome, i verovatnoca da dobijes na lotou je 50%, il' ces da dobijes il' neces. Sto bi znacilo da treba 50% ljudi u svakom kolu da dobije 7, jel da?

Btw, ova tema je trebala biti obrisana posle ovog posta. Zao mi je sto nisam mod pa da to licno uradim, jer sam ocigledno ovo prvi spazio.

Evo ja sam sposoban razmišljati logički i apstraktno, i slažem se da ti je šansa da prođeš oko 50%, mada ako bi ovo posmatrao strogo u geometrijskom prostoru Lobačevskog, mislim da ova šansa ipak mora da se aproksimira funkcijom odakle se vidi da je to ipak 50.099691% za dovoljno malo

Da, ali opet, treba i obratiti paznju na cinjenicu da zakrivljenost prostorvremena nije ekvivalentna u svim delovima univerzuma, pa ipak treba uzeti u obzir i difuznost i randomness ove pojave, sto nas trivijalno vodi do formule , gde je funkcija disperznosti gorepomenute velicine. Posmatramo li ovu f-ju () nad poljem , jasno je da verovatnoca ipak nije 50.099691, vec 50.099691001%.

da da... sve je to lepo objašnjeno u knjizi "Dogadjaji u geometrijskim prostorima - Verovatnoca pod lupom" od Lobačevskog. Obavezno štivo za sve koje zanima matematika!

Vidim da se zapostavlja jedan vrlo vazan efekat koji proizvode odredjene cestice
iz porodice leptona pri prolasku pokraj horizonta-dogadjaja... naime ako se umesto
hamiltonovog operatora u sredingerovoj jednacini koristi gore pomenuta f-ja (sa masom odredjenih leptona umesto ) dobija se verovatnoca da je jedan kandidat istovremeno i drugi!! ( ili neretko i sopstveni deda !! ) pa verovatnoca moze varirati od -24.1243 % do cak + 104.1241 %
E sada... ne bih znao da opisem u kilometrima ali kako mi se cini moramo jos uracunati i
moguce efekte samointerakcije usled nekontrolisanog ponasanja vremena ... Drugim recima ti mozes i biti odbijen na radno mesto jer SI VEC BIO primljen U skoroj BUDUCNOSTI ali si zamenjen samim sobom !!! ( gl. vreme . futur 3 prosli aorist perfekt u
buducnosti "hocejao zaposlijev sam bio sutra biti zaposlah"). Deluje zbunjujuce ali se diferenciranjem po sfernim kordinatama jedne piramide vrlo lako dobija nesto sto lici na jednacinu.

Naime... ne mozemo tek tako utvrditi ko je upravu. Predlazem da se organizuje javna debata na ovu temu sa mnogo kompetetnijim (apstraktnijim) strucnjacicma pa da se vidi na cemu smo... inace ja odoh da se obogatim na lotou , mozda dobijem i dve razlicite sedmice .


p.s. I base this on apsolutelly nothing , but it is TheTruth

Dakle, da zanemarimo dobacivanja iz publike tipa "Zaboravio si Plankovu konstantu", problem je u tome što ovde neko ne zna šta je verovatnoća. Sada neću pričati o formalnoj definiciji već o naivnoj definiciji

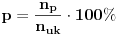
gde je p verovatnoća, n_p broj povoljnih događaja, n_uk broj ukupnih događaja, pri čemu mora biti jasno šta su sve mogući događaji, i na koliko načina se nešto može desiti.

Primer 1 (jednostavan primer)

Baca se kockica sa 6 strana. Koja je verovatnoća da će se dobiti broj deljiv sa 3.

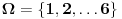
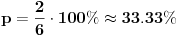
Skup elementarnih događaja je (to je šta se sve može desiti) , Dakle n_uk=6. Sa druge strane nas zanimaju slučajevi kad je taj broj deljiv sa 3. Dakle A={3,6}, tj n_p=2. Najzad . Kao što vidimo, mada imamo u osnovi dva slučaja (Broj je deljiv sa tri / broj nije deljiv sa 3), verovatnoća je

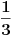Primer 2 (paradoks deMera)

Kao što vam je, verovatno, svima poznato, Blez Paskal (isti kome prog jezik Pascal duguje svoje ime), je bio jedan od utemeljivača Verovatnoće kao matematičke grane. Za deMera ne zna mnogo ljudi, ali i on ima svoje zasluge. U pitanju je matematičar-amater, koji je bio dobar prijatelj sa Paskalom, pomagao ga ponekad finansijski (deMer je bio plemićkog porekla) i strašno se interesovao za Paskalov rad. Uz to je bio kockar. Praktično je čitao Paskalove radove dok ih je ovaj pisao. Budući da je uz to znao nešto matematike sračunao je nešto zanimljivo...

Ne znam kako se zvala omiljena deMerova igra, ali se igrala na sledeći način:
Bacaju se 3 kockice, sabiraju vrednosti koje su dobijene. Igrači se klade na zbir.

DeMer je kontao:
mogućnost da je zbir 11 {(1,4,6),(1,5,5),(2,3,6),(2,4,5),(3,3,5),(3,4,4)};
mogućnost da je zbir 12 {(1,5,6),(2,4,6),(2,5,5),(3,3,6),(3,4,5),(4,4,4)};
dakle verovatnoće su jednake. Kladio se na 12 (dobija se više para) i - izgubio brdo para.

Paskal mu je kasnije objasnio da ovo nisu sve mogućnosti. Naime deMer je posmatrao kombinacije, a ne varijacije. U računu deMera, bitno je da su neki brojevi dobijeni, a ne na kojoj kockici je dobijen koji broj. Pravo rešenje bi bilo da je računao varijacije (to znači da je umesto ,npr (1,4,6), računao (1,4,6), (1,6,4), (4,1,6), (4,6,1), (6,1,4), (6,4,1) ) te mu dao formulu
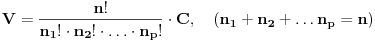
, gde su n_m pojavljivanja pojedinih brojeva. U ovom slučaju:
kad u kombinaciji imamo 3 mađu sobom različita broja tad je V=6C,
kad u kombinaciji imamo 2 jednaka broja i jedan različit od njih tad je V=3C,
kad u kombinaciji imamo 3 jednaka broja tad je V=C.

Dakle
mogućnosti da je zbir 11
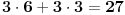
mogućnosti da je zbir 12

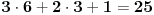
Pošto mu je Paskal sve to tako lepo objasnio, deMer je ostao prijatelj sa njim, ali mi nije poznato da li se i dalje kockao. Paskal je raskinuo prijateljstvo sa njim kasnije, kad je postao verski fanatik, ali to nije matematička priča.

Primer 3 (Arhimedov paradoks)

Odmah da kažem: Nije mi jasno zašto se ovo zove Arhimedovim paradoxom, ali ga možete naći pod tim imenom u literaturi.

Zamislite dva koncentrična kruga, od kojih je jedan dvostruko manjeg prečnika od drugog. Koja je verovatnoća da, slučajno izabrana, tetiva veće kružne linije seče manju kružnu liniju ?

Znamo da je tetiva zadata
a)pomoću centra i pravca.
b)pomoću svojih krajeva
[img][att_url][/img]
a) Podsetimo se da
1) Prava seče kružnu liniju akko je podnožje normale iz centra kruga na dotičnu pravu unutar kruga
2) Prava koja spaja središte tetive i centar kruga je normalna na tetivu.
3) koncentrični znači sa istim centrom

a₁)
Sad vidimo da, ako izaberemo prvo središte tetive, pa onda pravac tetive, tetiva seče malu kružnu liniju akko je centar tetive u malom krugu.

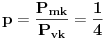
gde je P_mk površina malog, a P_vk površina velikog kruga.

a₂)
Ako prvo izaberemo pravac, onda znamo da središte tetive leži na pravoj normalnoj na dotični pravac(ubuduće - prava n). Verovatnoću merimo kao odnos dužina duži na pravoj n, konkretno d₁ -duž koja je u malom krugu, d₂ - duž koja je u velikom krugu



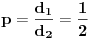
b) ako fixiramo jedan kraj tetive na velikom krugu, pa iz njega konstruišemo tangente na mali krug, vidimo da tetiva seče mali krug akko pripada uglu koji sačinjavaju dotične tangente ili njemu unakrsnom. Znači treba naći ugao pod kojim se iz dotične tačke vidi mali krug.

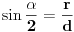
Kao što znamo, , gde je r poluprečnik malog kruga, d - rastojanje od tačke do centra malog kruga (a to je poluprečnik velikog kruga), pa je


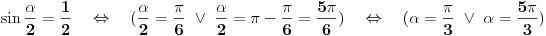
Dakle ugao pod kojim se vidi mali krug

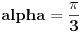
Sad

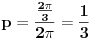
Daklem, verovatnoća zavisi od toga kako uzimamo da je zadata tetiva.

Napominjem ako ne znamo šta sve utiče na zadati proces, ne znamo ni verovatnoću. Ako se sva imena na tom tvom kokursu izvlače potpuna slučajno (npr na 3 identična listića se napišu sva imena, a onda se izvlači listić), onda ti je verovatnoća

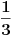
Ako se traži odgovarajuća stručnost verovatnoću je teško izračunati.

Ako ti znaš jednog člana komisije, drugi kandidat zna drugog člana, a treći nikog, verovatnoća je .

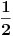
Ako ona dvojica znaju nekog iz komisije, a ti nikog, verovatnoća da dobiješ posao je 0

zahvaljujemo na izcrpnoj raspravi sudionika, medjutim još do sada nismo sigurni tko je u pravu, pa vas molimo, a usput ispricavamo na žucnim reprikama, da nam konacno recete tko ce piti viski a tko sok na ovom pitanju i tko ce to platit ?.
zahvaljujemo!

Veruj mi da znam šta je verovatnoća i skup elementarnih događaja, ali molim te mani me se ova dva školska paradoksa, jer to toliko nema veze sa ovim kvarnerexpress-ovim problemom da ja nemam reči. Pre svega mi ne znamo verovatnoće tih elementarnih događaja, tj. kolika je verovatnoća da bilo ko od njih dobije posao, kao što ne znamo ni kriterijum po kome neko dobija posao. Kako bilo, verovatnoća će pre biti 1:3 nego 1:2 ako se posmatra kao neki "savršeni slučaj", a mi ovo, na osnovu datih nam informacija ni ne možemo da posmatramo drugačije. Dakle treba na "komisiju" gledati kao na apsolutno nepristrasno telo koje u krajnjoj liniji daje nasumičan rezultat, tj. sva tri kanditata imaju podjednake šanse da prođu.
Ništa Paskal, ništa De Mer, ništa Arhimed, ništa slonovi.

Ako misliš da komisije biraju kandidate slučajno, onda stvarno veze nemaš sa verovatnoćom.

Ako ti zaista misliš da se ovako izračunava verovatnoća, to najbolje govori o tvom znanju. U svakom slučaju, voleo bih da mi objasniš kako bi ti izračunao verovatnoću, jer po onome što mi znamo meni se čini da sva tri kandidata imaju podjednake verovatnoće da prođu.



Argh! Naravno da ne biraju kandidata slučajno, ali po količini informacija koje mi posedujemo može da se svede na tako uprošćen model. Damn. Odustajem. Ako neko drugi ima živaca da se ubećuje sa tvrdoglavima, be my guest :D

Ja bih se ubedjivao, ali ne mogu sad, mom prijatelju ulecu unajvece slonovi kroz prozor, pa moram da mu pomognem...

Drago dete, pokušavam da kažem da nemamo dovoljno informacija, da bismo mogli da tvrdimo da je raspodela verovatnoća uniformna. Na, očigledno tebi nerazumljiv način, pokušavam da kažem da, ako je raspodela uniformna, tj ako svi kandidati imaju jednaku verovatnoću da budu izabrani, onda ta veovatnoća iznosi gde je n - broj kandidata. Mi čak ni ne znamo koji su uslovi koje kandidati moraju da zadovolje, kao ni u kolikoj meri. Na ovom topiku preovlađuje šaljiv ton, te pokušaj da i moju prethodnu poruku shvatiš kao šaljivu, a ne uvredljivu. Nisam mislio da procenjujem tvoje znanje, ali kažem još 1 da nemamo dovoljno podataka. Na celoj temi je bilo i poprilično postova koji govore potpuno netačne stvari.

Najzad, ako ima 3 ravnopravna kandidata veovatnoća je 1/3, tj 33.333333 %

Znaci odavno se ovoliko nisam nacitao gluposti...
Mnogo ste dobri! Znaci fukcije, Lobacevski, podaci, verovatnoca, slonovi :-)

Tema zaključana (iz očiglednih razloga).