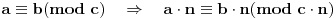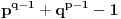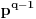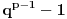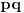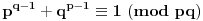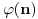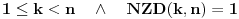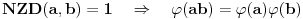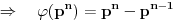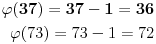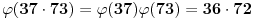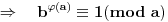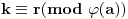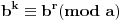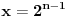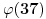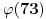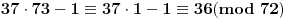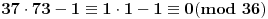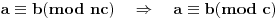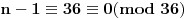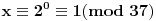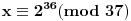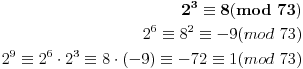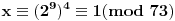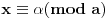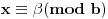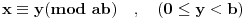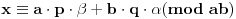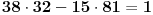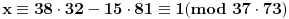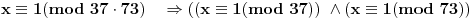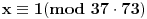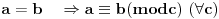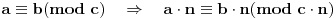Broj je deljiv sa , jer je deljivo sa , kao i (na osnovu male Fermaove teoreme, koja je specijalni slucaj Ojlerove teoreme). Slicno je broj deljiv i sa , pa je deljiv i sa . Zbog toga je . Za ovaj drugi nemam vremena sad da kucam, pa ce postaviti resenje sutra ili prekosutra (ako me neko ne preduhitri).

Za Ojlerovu funkciju važi:
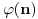
je broj brojeva k, takvih da

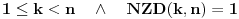
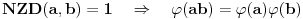
p-prost

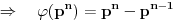
Npr




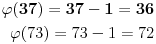
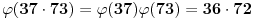Ojlerova teorema
NZD(a,b)=1


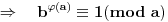Posledica Ojlerove teoreme
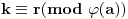
Neka je i NZD(a,b)=1
Tada je

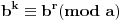
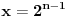
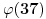
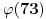
Prvo ćemo videti čemu je kongruentno po modulu 37, pa po modulu 73. No, pre toga moramo da vidimo čemu je kongruentno samo n-1 po modulu =36 te po modulu =72




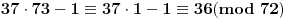
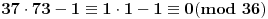
Ovde smo mogli da koristimo stav

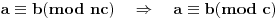
pa bi smo dobili


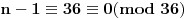
Obeležimo sa

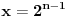
Daklem



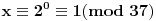
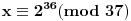
Za ovo drugo računajmo


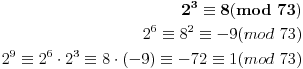
Dakle


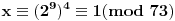
Eh, sad kineska teorema o ostacima

Kineska teorema o ostacima
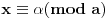
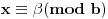
Ako je i i NZD(a,b)=1, tada jednačina

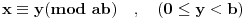
ima jedinstveno rešenje po y.

Uz dodatak

Posledica Kineske teoreme o ostacima
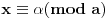
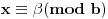
Ako je i i ap+bq=1, tada je


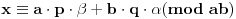
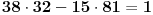
Daklem, pošto je , vidimo da je


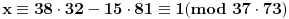
Ovaj drugi deo mogao je i bez posledice kineske teoreme, jer



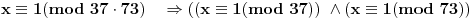
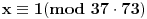
pa bi smo do rešenja stigli praktično pogađanjem. Obrati pažnju da bez kineske teoreme ne smemo da tvrdimo da je , zbog jedinstvenosti koju nam daje baš kineska teorema.

Najzad da napomenem

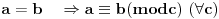
te stoga nema potrebe da koristiš jednakosti.

Za kraj, još jedna teorema