|
|
[ DraganK @ 27.05.2005. 08:08 ] @
|
| Kako od nekog velikog broja n naći broj svih uzajamno prostih sa n, to je valjda Ojlerova funkcija. Recimo:
Kako izračunati F(57)? |
[ Srđan Krstić @ 27.05.2005. 09:31 ] @
[ DraganK @ 27.05.2005. 10:04 ] @
Ok. Thanks...
Ali bi to u ovom primeru, za 57, bilo kako...?
[ Srđan Krstić @ 27.05.2005. 10:32 ] @
? Pa zar nije vec dovoljno jasno ?
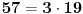
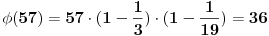
[ DraganK @ 28.05.2005. 12:53 ] @
Uf da...
Hvala puno.
Pozdrav...
[ Cabo @ 28.06.2005. 10:36 ] @
Za Ojlerovu funkciju važi i ovo:
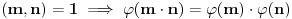
To jest Ojlerova funkcija je multiplikativna aritmetička funkcija. Dalje, 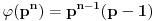 , što za 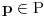 daje 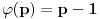 .
Konkretno, 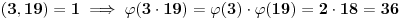 .
[Ovu poruku je menjao Cabo dana 28.06.2005. u 11:37 GMT+1][ milicas @ 29.06.2005. 09:03 ] @
Negde sam videla da Ojlerova f-ja slika 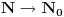 . A od cega je 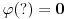 ? Koliko je 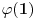 ? [ Bojan Basic @ 29.06.2005. 10:52 ] @
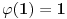 , ali to što si videla nije pogrešno jer prilikom takvog zapisivanja ne podrazumeva se da sve vrednosti kodomena moraju biti uključene u skup vrednosti funkcije, odnosno kodomen je bilo koji nadskup skupa vrednosti funkcije. Možeš bez problema reći 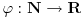 i opet nisi pogrešila.
[Ovu poruku je menjao Bojan Basic dana 29.06.2005. u 12:25 GMT+1][ milicas @ 29.06.2005. 11:21 ] @
Vidi ovo! Sad mi nesto pade na pamet. Jos u januaru sam videla zadatak:
Neka je 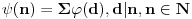 a  Ojlerova f-ja. Ako je p prost, naci 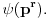
Ispostavlja se da je 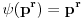 ali mora da bude 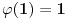 da bi se nesto skratilo. Ja sam mislila da se po definiciji uzima 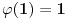 , pa sam bila zbunjena...
Naravno, znam da je "legitimno" i 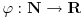 :) ... [ Bojan Basic @ 29.06.2005. 11:26 ] @
Joj, ja sam magarac, pritisnuo sam pogrešan taster pri kucanju. Ispravio sam sad, izvinjavam se na grešci.
[ Cabo @ 30.06.2005. 19:47 ] @
Ukoliko za neku funkciju 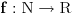 važi: 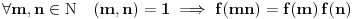 i 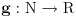 , 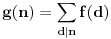 , onda se može lako dokazati da i za  važi 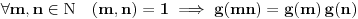 , odnosno i  je multiplikativna aritmetička funkcija. Za 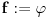 i 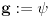 se dobija tvrđenje.
[Ovu poruku je menjao Cabo dana 30.06.2005. u 20:50 GMT+1][ uranium @ 01.07.2005. 07:20 ] @
Dirichlet-ov proizvod se definiše kao:
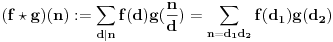
Ako su  i  multiplikativne, onda je i 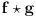 .
Dokaz:
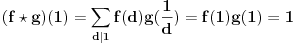
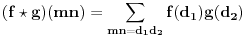 ,
pošto su  i  uzajamno prosti, onda za svako 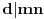 važi: 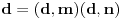 , pa dobijamo:
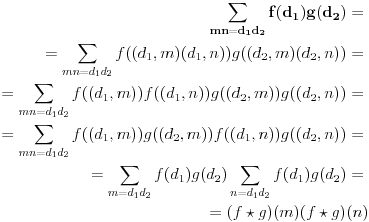 ,
Pretposlednja jednakost važi zato što : iz 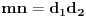 , sledi i 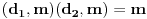 (i analogno 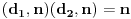 ). Dakle, svaka faktorizacija 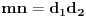 generiše jedinstvene (do na poredak) faktorizacije 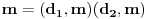 i 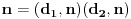 , kao i obrnuto svake dve faktorizacije 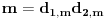 i 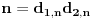 generišu jedinstvenu (do na poredak) faktorizaciju 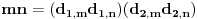 za koju je 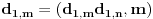 , 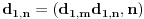 i analogno za 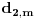 i 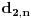 .
Time je dokazano tvrđenje.
Primetimo najzad da je funkcija 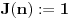 multiplikativna i da je 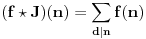 takođe multiplikativna, pod uslovom da je i f takva.
Što se tiče zadatka, sada nije teško pokazati i 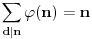 (naravno, sam zadatak se može rešiti i daleko prostije)
[Ovu poruku je menjao uranium dana 01.07.2005. u 08:23 GMT+1]
[Ovu poruku je menjao uranium dana 01.07.2005. u 08:25 GMT+1]
[Ovu poruku je menjao uranium dana 01.07.2005. u 08:35 GMT+1][ uranium @ 01.07.2005. 08:39 ] @
I još nešto. Cabo, da li bi mogao malo da obrazložiš: Citat: Cabo: ...odnosno i  je multiplikativna aritmetička funkcija. Za 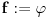 i 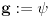 se dobija tvrđenje.
jer ne vidim kako multiplikativnost f-je  povlači tvrđenje, a da prethodno ne upotrebiš samo tvrđenje 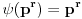 
[ Nedeljko @ 01.07.2005. 09:27 ] @
Citat: uranium: Dirichlet-ov proizvod se definiše kao:
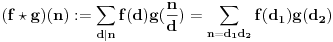
Nisam znao da se konvolucija aritmetičkih funkcija zove još i Dirihletovim proizvodom. U svakom slučaju, za ovu operaciju se koristi termin konvolucija.
[Ovu poruku je menjao Nedeljko dana 01.07.2005. u 10:28 GMT+1][ uranium @ 01.07.2005. 09:56 ] @
Kad smo već kod konvolucije, da li bi mogao da objasniš geometrijski smisao i motivaciju za uvođenje te operacije (mislim na ono sa integralima - nikako da ukapiram  ).
Sad mi je nešto palo na pamet.
Definicija multiplikativnosti f-je  zahteva da važi: 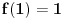 .
Ako za f-ju  važi 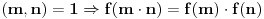 , onda je ili 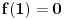 ili 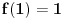 .
Jer ako je 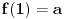 , onda mora biti 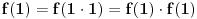 tj. 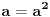 .
Dakle, ili je 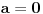 ili 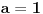 . E sad, ako bi bilo 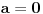 onda bi bilo i 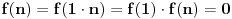 (jer je 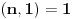 za svako  ). Znači, jedino nula f-ja bi mogla biti multiplikativna pri ovakvoj definiciji, a to je skroz bezveze, dakle, mora biti 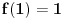 .
S druge strane, imam utisak da je neko namerno prilagodio definiciju Ojlerove f-je tako da ona postane multiplikativna u smislu gornje definicije. Oduvek mi je malo "štrčala" 0 u definicije f-je 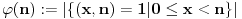 . Ako bi u ovoj definiciji bilo, 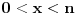 (a to mi izgleda mnogo prirodnije), onda bi bilo 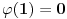 pa bi ono što je milicas našla u vezi sa kodomenom bilo potpuno opravdano!
Da li neko može da "iskopa" negde originalnu Ojlerovu definiciju ove f-je?
[ Nedeljko @ 02.07.2005. 00:23 ] @
Citat: uranium: S druge strane, imam utisak da je neko namerno prilagodio definiciju Ojlerove f-je tako da ona postane multiplikativna u smislu gornje definicije. Oduvek mi je malo "štrčala" 0 u definicije f-je 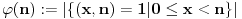 . Ako bi u ovoj definiciji bilo, 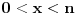 (a to mi izgleda mnogo prirodnije), onda bi bilo 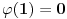 pa bi ono što je milicas našla u vezi sa kodomenom bilo potpuno opravdano!
Da li neko može da "iskopa" negde originalnu Ojlerovu definiciju ove f-je?
A zašto ne staviš da je 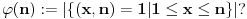
Primeti da je množenje polinoma zapravo jedna konvolucija nizova, kao i formalno množenje redova. Kontinualni analogon bi bio
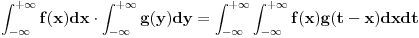
pod uslovom da prva dva integrala postoje i da pritom apsolutno konvergiraju. [ uranium @ 02.07.2005. 07:56 ] @
Citat: Nedeljko: A zašto ne staviš da je 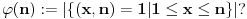
Može i tako 
Citat: Nedeljko:
...Kontinualni analogon bi bio
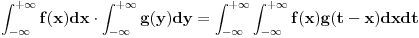
pod uslovom da prva dva integrala postoje i da pritom apsolutno konvergiraju.
Sve je to O.K. ali definicija kaže da dotična formula opisuje meru preklapanja datih funkcija kada jednu od njih (sve jedno je koju) "pomeraš" preko druge - e to mi baš nije očigledno 
[ Cabo @ 04.07.2005. 20:57 ] @
Citat: uranium: I još nešto. Cabo, da li bi mogao malo da obrazložiš:
jer ne vidim kako multiplikativnost f-je  povlači tvrđenje, a da prethodno ne upotrebiš samo tvrđenje 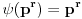 :)
Ja nisam ni rekao da je  multiplikativna, već da je  multiplikativna, a da se može lako dokazati da odatle sledi da je  multiplikativna.
[Ovu poruku je menjao Cabo dana 04.07.2005. u 22:05 GMT+1][ uranium @ 05.07.2005. 00:04 ] @
Ako upotrebiš modus ponens videćeš da si to ipak rekao 
[ Cabo @ 05.07.2005. 17:01 ] @
Nije mi cilj da se ovde natežem oko sitnica, pa ću dati kompletno tvrđenje i dokaz. Ovo sam imao na umu.
Tvrđenje: Ukoliko za neku funkciju 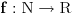 važi: 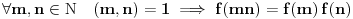 , odnosno ako je funkcija  multiplikativna aritmetička funkcija, onda je funkcija 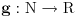 , definisana sa 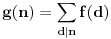 , takođe multiplikativna aritmetička funkcija, odnosno važi: 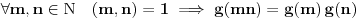 .
Dokaz: Neka je 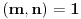 . Imamo:
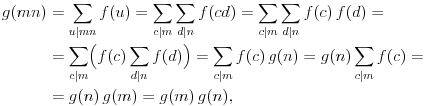
čime je tvrđenje dokazano.
E, sad, ako primenimo ovo tvrđenje na funkciju  , koja je očito multiplikativna aritmetička funkcija, dobićemo da je i funkcija 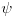 takođe multiplikativna aritmetička funkcija, pošto je 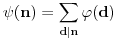 .
[Ovu poruku je menjao Cabo dana 05.07.2005. u 18:04 GMT+1][ Relaja @ 21.02.2007. 22:00 ] @
U traganju za pomoci za jedan zadatak iz programiranja naidjoh na ovaj topic , a mislim da je moj problem upravo povezan njim.
No, nemojte mi zameriti ako sam pitao nesto sto je vec pomenuto, jer sam se zaista izgubio u silnim jednacinama i znacima :).
Dakle , problem glasi : koliko ima parova (a,b) tako da su oni uzajamno prosti i 1<= a,b <= (N<=10^9) ?
Ali, mislim da mi Ojlerova formula koju je pomenuo Srdjan Krstic ne znaci mnogo jer mi rastavljanje na cininioce stvara veliku slozenost.
Dakle, kako bih to mogao efikasnije da izracunam?
Hvala
Edit: Video sam resenje , i u stvari se sve svodi na optimizacije..Tako da nema nicega novog.
[Ovu poruku je menjao Relaja dana 23.02.2007. u 09:33 GMT+1]
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|