Da je resiv to stoji jer ako si obratio paznju na pravila svaka kocka 3x3 koja cini celokupnu tablu koja je recimo 9x9, mora da sadrzi u sebi brojeve od 1 do 9. Znaci da svaka kocka 3x3 podleze tom pravilu a istovremenom svaka kolona ili red table (znaci 9 polja) mora da sadrze sve brojeve od 1 do 9 bez ponavljanja.
Sad koliko je minimalan broj da bi mogao da dodjes do resenja to je vec malo teza stvar najbolje bi mozda bilo testirati na kompu tako ces se lako uveriti sa koliko polja ce biti u stanju da nadje resenje doduse mora da postoji popunjen odredjen broj polja da bi postojalo samo jedno resenje inace ako fali vise od pola table u tom slucaju mislim da mozes da lupas brojeve i da namestas sam kako tebi odgovara...
Ako zelis da malo bolje prostudiras stvar mozes da skines igru sudoku pa da ti kompjuteru zadajes zadatke koje treba da resava ili obrnuto:
http://www.freedownloadsoft.com/Sudoku

Nagadjam da bi igra mogla da se resava kao sistem linearnih jednacina. Svako polje bi bila promenljiva a sistem bi se sastojao od 27 jednacina i 81 promenljive (ustvari manje posto bi neke imale vrednost na pocetku igre).
Za resenje igre se usvaja ono resenje u kome su sve promenljive celobrojne i pripadaju intervalu od 1 do 9. Ovakav model bi se mogao resavati "potpunim" pretrazivanjem.

Sistem bi bio oblika:
x11+x12+...+x19=45
... (zbir svakog reda)
x11+x12+...+x33=35
... (zbir svakog kvadrata)
x11+x21+...+x91=45
... (zbir svake kolone)

Ne znam šta bi osiguralo jedinstvenost brojeva u vrstama, kolonama i kvadratima ako bi se Sudoku posmatrao kao sistem jednačina. Nisam siguran da je ovo pravo rešenje. Dokazi?

Uzgred, jesi li pogledao http://en.wikipedia.org/wiki/Sudoku?

Je l' ima neko ideju za generisanje ovakvih matrica?

Ovako ja to vidim: postoji samo 16 razlicitih resenja, sve ostalo moze da se postigne pomeranjem pojedinacnih kolona ili celih "trokolona" ili kako god to moglo da se nazove. Nisam siguran da nisam nesto prevideo, ali neka me neko razuveri ako moze...

??????
Pojasni sta ti znaci da ima samo 16 resenja.

16 razlicitih resenja koje se nemogu svesti jedna na druga. Bilo koje drugo resenje se moze svesti na jedno i samo jedno od ovih 16, koristeci zamenu mesta redova (kolona) u okviru horizontalnih (vertikalnih) blokova, kao i zamena mesta blokova (blok = 3 vezana kvadrata).

Ne možeš da menjaš blokove, već samo "trokolone" i "troredove", a i kolone i redovi se mogu menjati samo u okviru iste "trokolone" i "troreda".
Ni ja ne razumem tačno odakle ti to da postoji samo 16 rešenja (ne računajući varijacije nastale razmeštanjem (tro)redova i (tro)kolona), ako možeš obrazloži.

na to sam i mislio, blok==trokolona (trored)



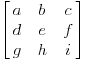
u sledecem kvadratu (3x3) ovi redovi abc, def, ghi, se mogu pojaviti isti (samo na drugoj visini) ili u 2+1 grupama, npr. ab+c, de+f, gh+i sto ce u sledecim kvadratima da da: (de+i, gh+c, ab+f) i (gh+f, ab+i, de+c)

dalje u tri troredi mogu biti 4 kombinacije 3\3\3; 3\3\2+1; 3\2+1\2+1; ili 2+1\2+1\2+1
isto vazi i za kolone, pa je to 4*4=16 konfiguracija. E sad da se svaka moze svesti na ovih sesnaest samo predpostavljam, mada bi mi nekako logicno doslo. U krajnjoj liniji ako neko ima vremena (ja sasvim sigurno trenutno nemam), neka dokaze ili opovrgne...


<sub>[Ovu poruku je menjao Leftist dana 26.08.2005. u 02:49 GMT+1]

[Ovu poruku je menjao Leftist dana 26.08.2005. u 02:51 GMT+1]</sub>

Dim a(9) As Byte
Dim b(81) As Byte
Dim c(81) As Byte
Dim k(729) As Byte
Dim i, isp
Private Sub Form_Load()
Open "c:\sudoku.txt" For Append As 1
Randomize Timer
gen729
i = 0
p1 = 0
While i < 81
i = i + 1
c(i) = 1
ispravno (p1)
While isp = "ne"
c(i) = c(i) + 1
While c(i) = 10
c(i) = 0
i = i - 1
c(i) = c(i) + 1
Wend
ispravno (p1)
Wend
Wend
Print #1, ""
Print #1, Date;
Print #1, Time
Print #1, ""
For g = 0 To 8
For o = 1 To 9
Print #1, b(g * 9 + o);
If o = 3 Then Print #1, Chr(124);
If o = 6 Then Print #1, Chr(124);
Next
Print #1, ""
If g = 2 Then Print #1, "--------------------------"
If g = 5 Then Print #1, "--------------------------"
Next
Close 1
End
End Sub
Sub ispravno(t)
isp = "da"
For x = 1 To 81
b(x) = 0
Next
For x = 1 To i
p1 = plus(k((x - 1) * 9 + c(x))) + sab(x Mod 9)
If b(p1) <> 0 Then isp = "ne"
b(p1) = Int((x - 1) / 9) + 1
Next
t = p1
y = Int(1 + (t - 1) / 9)
x = t - (y - 1) * 9
If x < 4 Then xx = 1
If x > 3 And x < 7 Then xx = 4
If x > 6 Then xx = 7
If y < 4 Then yy = 1
If y > 3 And y < 7 Then yy = 4
If y > 6 Then yy = 7
For s = (yy - 1) * 9 + xx To (yy - 1) * 9 + xx + 2
If t <> s And b(t) = b(s) Then isp = "ne"
Next
For s = yy * 9 + xx To yy * 9 + xx + 2
If t <> s And b(t) = b(s) Then isp = "ne"
Next
For s = (yy + 1) * 9 + xx To (yy + 1) * 9 + xx + 2
If t <> s And b(t) = b(s) Then isp = "ne"
Next
For s = (y - 1) * 9 + 1 To (y - 1) * 9 + 9
If t <> s And b(t) = b(s) Then isp = "ne"
Next
For s = x To 81 Step 9
If t <> s And b(t) = b(s) Then isp = "ne"
Next
End Sub
Sub gen9()
Dim pom(9)
For q = 1 To 9
a(q) = 0
pom(q) = 0
Next
For q = 1 To 9
ok = 0
While ok = 0
p = Int(Rnd * 9) + 1
If pom(p) = 0 Then pom(p) = 1: a(q) = p: ok = 1
Wend
Next
End Sub
Sub gen729()
For s = 1 To 81
gen9
For t = 1 To 9
k((s - 1) * 9 + t) = a(t)
Next t
Next s
End Sub
Function plus(pk)
If pk = 1 Then plus = 0
If pk = 2 Then plus = 1
If pk = 3 Then plus = 2
If pk = 4 Then plus = 9
If pk = 5 Then plus = 10
If pk = 6 Then plus = 11
If pk = 7 Then plus = 18
If pk = 8 Then plus = 19
If pk = 9 Then plus = 20
End Function
Function sab(lp)
If lp = 1 Then sab = 1
If lp = 2 Then sab = 4
If lp = 3 Then sab = 7
If lp = 4 Then sab = 28
If lp = 5 Then sab = 31
If lp = 6 Then sab = 34
If lp = 7 Then sab = 55
If lp = 8 Then sab = 58
If lp = 0 Then sab = 61
End Function



Gore vam je program u vb za generisanje. Potrebno je samo da kreirate prazan file "c:\sudoku.txt". Nisam se puno zamlacivao sa matematikom ali broj kombinacija je mnogo veci od 16, i reda je velicine 10^21. Program radi vrlo brzo (par desetinki sekunde). Tiranine, odgovor na tvoje pitanje se ne moze dati precizno. Zavisi od toga kako je zagonetka postavljena

Evo šta kažu na Vikipediji (http://en.wikipedia.org/wiki/Sudoku):

BiF, da li tvoje VB resenje za generisanje sudokua daje slagalicu sa jedinstvenim resenjem
ili o tome ne vodi racuna?

Nisam hteo da gnjavim, ali kad je vec tema otvorena posle godinu dana da nesto dodam.
Ovde se izgleda brka broj mogucih rasporeda cifara 1...9, tako da zadovolji uslove nepojavljivanja u bloku, redu, koloni,( koji se valjda i moze izracunati) sa samim zadatkom koji polazi od delimicno popunjene matrice, i koji(zadatak) logickim rasudjivanjem treba da dovede do jednoznacnog resenja.
Na intrenetu nisam nasao bilo kakvo matematicko objasnjenje, mozda je neko bio bolje srece?

Naslov ove teme je: „Sudoku, matematičko objašnjenje“. Dakle, radi se o matematičkom problemu, a ne o problemu kompleksnosti i optimizacije algoritma za programsko izračunavanje rešenja.

Pa, valjda su pitanja ocene kompleksnosti algoritama matematička.

U širem smislu da, ali ne i u užem smislu. To je pitanje kojim se bavi nauka zvana „Computer science“.