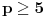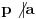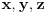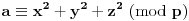[ Bojan Basic @ 30.05.2005. 17:52 ] @
|
[ uranium @ 18.08.2005. 02:39 ] @
Dokazaću malo opštije tvrđenje, zbog čega mi i treba ovoliki uvod.
Definicija 1. Neka je  prost broj i prost broj i 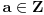 uzajamno prost sa uzajamno prost sa  , onda za , onda za  kažemo da je kvadratni ostatak po modulu kažemo da je kvadratni ostatak po modulu  akko postoji akko postoji 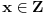 za koje važi za koje važi 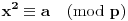 . .Definicija 2. Neka je  prost broj i prost broj i 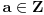 uzajamno prost sa uzajamno prost sa  , onda za , onda za  kažemo da je ne-kvadratni ostatak po modulu kažemo da je ne-kvadratni ostatak po modulu  akko nije kvadratni ostatak po modulu akko nije kvadratni ostatak po modulu  . .(ne znam kako bih preveo quadratic non-residue) Nadalje,  će uvek označavati neki neparan prost broj, a će uvek označavati neki neparan prost broj, a 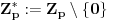 . .Lema 1. Ako je 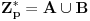 , gde je , gde je  skup svih kvadratnih ostataka po modulu skup svih kvadratnih ostataka po modulu  a a  skup svih ne-kvadratnih ostataka po modulu skup svih ne-kvadratnih ostataka po modulu  , onda je , onda je 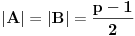 . .Dokaz. Na osnovu prethodnih definicija jasno je da važi 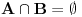 . . Ako je 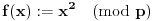 , i ako je , i ako je 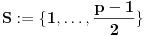 , onda je , onda je 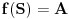 . . Naime, 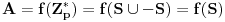 , jer je , jer je 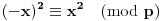 . .Pokazaćemo da je  i injekcija na i injekcija na  . .Ako bi za neke 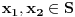 bilo bilo 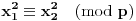 , onda sledi , onda sledi 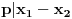 ili ili 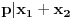 . .Budući da 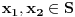 , u prvom slučaju sledi da je , u prvom slučaju sledi da je 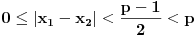 pa mora biti pa mora biti 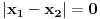 tj. tj. 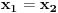 , a drugi je nemoguć zbog procene , a drugi je nemoguć zbog procene 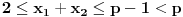 . .Sada imamo da je 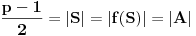 , odakle i sledi tvrđenje. , odakle i sledi tvrđenje. Lema 2. Ako je 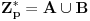 , gde je , gde je  skup svih kvadratnih ostataka po modulu skup svih kvadratnih ostataka po modulu  a a  skup svih ne-kvadratnih ostataka po modulu skup svih ne-kvadratnih ostataka po modulu  , onda: , onda:1. 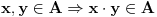 2.  3. 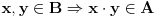 Dokaz. Primetimo prvo da je, za svako fiksirano 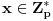 , f-ja , f-ja 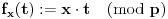 bijekcija na bijekcija na 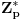 . .Ako je 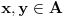 , onda na osnovu definicije 1. sledi da postoje brojevi , onda na osnovu definicije 1. sledi da postoje brojevi 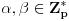 takvi da važi takvi da važi 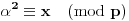 i i 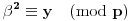 , pa dobijamo , pa dobijamo 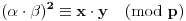 , tj. , tj. 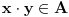 . .Ako je 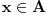 a a 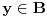 , onda, budući da je , onda, budući da je  fiksirano, možemo posmatrati f-ju fiksirano, možemo posmatrati f-ju 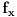 na skupu na skupu  . Iz dela pod 1. sledi . Iz dela pod 1. sledi 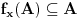 a iz injektivnosti sledi a iz injektivnosti sledi 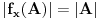 , pa imamo da je , pa imamo da je 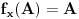 . .Sada je jasno da ne može biti 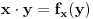 element skupa element skupa  , jer bi u protivnom ispalo da za neko , jer bi u protivnom ispalo da za neko  važi važi 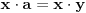 , pa bi, posle skraćivanja sa , pa bi, posle skraćivanja sa  ispalo da je ispalo da je 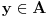 (što je kontradikcija). (što je kontradikcija).Ako je 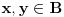 , onda možemo posmatrati f-ju , onda možemo posmatrati f-ju 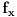 na skupu na skupu  , pa koristeći dokazani deo pod 2. kao i injektivnost f-je, na analogan način kao i prethodnom delu, uz korišćnje rezultata , pa koristeći dokazani deo pod 2. kao i injektivnost f-je, na analogan način kao i prethodnom delu, uz korišćnje rezultata 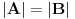 iz Leme 1, dobiti iz Leme 1, dobiti 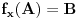 . Sada, na isti način kao i u delu pod 2, sledi da . Sada, na isti način kao i u delu pod 2, sledi da 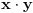 mora biti element skupa mora biti element skupa  . . (Inače, ove dve leme još lakše slede ako znamo da je za svako prosto p, grupa 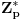 ciklična, ili, što je isto: da za svako prosto ciklična, ili, što je isto: da za svako prosto  postoji "primitive root modulo postoji "primitive root modulo  "). ").Lema 3. Ako je 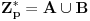 , gde je , gde je  skup svih kvadratnih ostataka po modulu skup svih kvadratnih ostataka po modulu  a a  skup svih ne-kvadratnih ostataka po modulu skup svih ne-kvadratnih ostataka po modulu  , onda važi: , onda važi:1. za 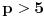 , postoje , postoje 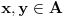 za koje važi za koje važi 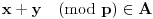 . .2. za 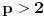 , postoje , postoje 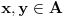 za koje važi za koje važi 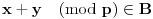 . .Dokaz. 1. Možemo iskoristi identitet: 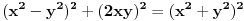 , pazeći pri tom da , pazeći pri tom da 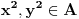 budu takvi da nije ni budu takvi da nije ni 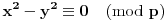 , ni , ni 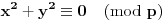 , a to je uvek moguće za , a to je uvek moguće za 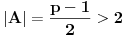 tj. za tj. za 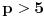 . .2. Budući da je 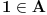 , možemo posmatrati f-ju , možemo posmatrati f-ju 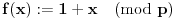 , , 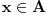 . .Uzmimo da je 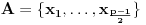 , pri čemu je , pri čemu je 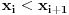 za svako za svako  . .Ako bi za neko  bilo bilo 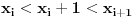 , onda bi moralo biti , onda bi moralo biti 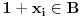 , pa bi to bio kraj dokaza. , pa bi to bio kraj dokaza.A ako bi za svako  bilo bilo 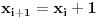 , onda bi imali da je , onda bi imali da je 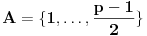 , pa bi moralo biti , pa bi moralo biti 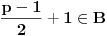 . . Lema 4. Svaki element skupa 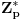 , gde je , gde je 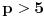 , može se predstaviti kao zbir: , može se predstaviti kao zbir:1. Dva kvadratna ostatka, za 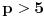 2. Dva ne-kvadratna ostatka, za 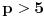 3. Jednog kvadratnog ostatka i jednog ne-kvadratnog ostatka, za 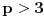 Dokaz: Ako je 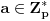 , onda postoji jedinstveno , onda postoji jedinstveno 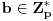 za koje važi za koje važi 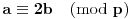 , (jer je 2 inverzibilno po modulu , (jer je 2 inverzibilno po modulu  ), ),pa ako stavimo da je 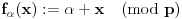 , onda se sve particije broja , onda se sve particije broja  u grupi u grupi 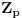 mogu predstaviti kao mogu predstaviti kao 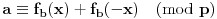 pri čemu se pri čemu se  "šeta" kroz "šeta" kroz 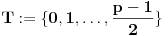 . .Budući da je f-ja 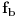 bijekcija i da je bijekcija i da je 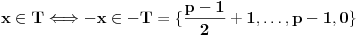 , dobijamo da se svi elementi skupa , dobijamo da se svi elementi skupa 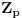 pojavljuju tačno jedanput kao sabirci, u pomenutim razlaganjima, osim što se element pojavljuju tačno jedanput kao sabirci, u pomenutim razlaganjima, osim što se element  javlja i kao javlja i kao 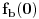 i kao i kao 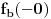 , a što je u stvari jedno te isto. Primetimo i to da su parovi jedinstveno određeni, tj. za dato , a što je u stvari jedno te isto. Primetimo i to da su parovi jedinstveno određeni, tj. za dato 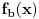 , jedini broj (po modulu p) koji sa njim pravi razlaganje broja , jedini broj (po modulu p) koji sa njim pravi razlaganje broja  (po modulu p) je upravo (po modulu p) je upravo 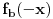 . .Neka su nadalje,  i i  skupovi kvadratnih, odnosno ne-kvadratnih ostataka po modulu skupovi kvadratnih, odnosno ne-kvadratnih ostataka po modulu  . .Neka je 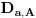 broj razlaganja broja broj razlaganja broja  po modulu po modulu  , u kojima su oba sabirka iz skupa , u kojima su oba sabirka iz skupa  , (analogan smisao ima i oznaka , (analogan smisao ima i oznaka 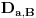 ) i neka je ) i neka je 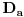 broj "mešovitih" razlaganja broja broj "mešovitih" razlaganja broja  po modulu po modulu  , u kojima je jedan sabirak iz , u kojima je jedan sabirak iz  a drugi iz a drugi iz  . .Pokazaćemo sada da važi: a) Ako su 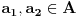 , onda je , onda je 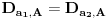 , , 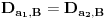 i i 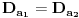 b) Ako su 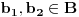 , onda je , onda je 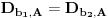 , , 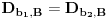 i i 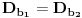 c) Ako je  i i 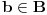 , onda je , onda je 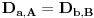 , , 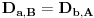 i i 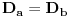 Označimo jedan (bilo koji) od skupova  i i  sa sa  . .Ako su 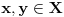 , onda, na osnovu Leme 2. postoji , onda, na osnovu Leme 2. postoji 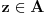 , tako da važi , tako da važi 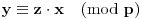 , pa svakom razlaganju broja , pa svakom razlaganju broja 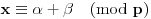 odgovara jedinstveno razlaganje broja odgovara jedinstveno razlaganje broja 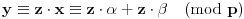 , a pošto je , a pošto je 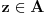 , na osnovu Leme 2. sledi da će i , na osnovu Leme 2. sledi da će i 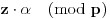 pripadati istom skupu ( pripadati istom skupu ( ili ili  ) kao i ) kao i  i analogno, i analogno, 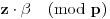 pripadaće istom skupu ( pripadaće istom skupu ( ili ili  ) kao i ) kao i  . Dakle, vidimo da se "struktura" tih razlaganja ne menja. Pošto možemo napraviti i analogan prelaz sa razlaganja broja . Dakle, vidimo da se "struktura" tih razlaganja ne menja. Pošto možemo napraviti i analogan prelaz sa razlaganja broja  na razlaganja broja na razlaganja broja  , slede tvrđenja pod a) i b). (Koja u stvari pokušavaju da kažu da prilikom razmatranja broja razlaganja elemenata iz , slede tvrđenja pod a) i b). (Koja u stvari pokušavaju da kažu da prilikom razmatranja broja razlaganja elemenata iz  ili ili  , nije bitno kog "predstavnika" tih skupova posmatramo.) , nije bitno kog "predstavnika" tih skupova posmatramo.)Dokaz tvrđenja pod c) je potpuno analogan prethodnom, uz jedinu razliku da 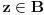 , pa prema Lemi 2, "struktura" razlaganja se "invertuje" tj. ako je , pa prema Lemi 2, "struktura" razlaganja se "invertuje" tj. ako je 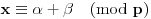 , (neka je npr. , (neka je npr. 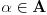 ) onda će sabirci u pridruženom razlaganju broja ) onda će sabirci u pridruženom razlaganju broja 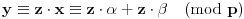 pripadati "suprotnom" skupu (onda je npr. pripadati "suprotnom" skupu (onda je npr. 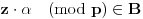 ). ).Sada, na osnovu Leme 3. i tvrđenja pod a) i b) mora da važi 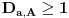 , , 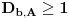 za svako za svako  i svako i svako 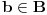 , pa, na osnovu tvrđenja c), dobijamo da je i , pa, na osnovu tvrđenja c), dobijamo da je i 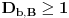 i i 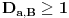 , odakle slede tvrđenja pod 1. i 2. , odakle slede tvrđenja pod 1. i 2.Da bi važilo i tvrđenje pod 3. dovoljno je pokazati da je za neko 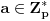 važi važi 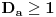 , jer bi na osnovu a), b) i c) odmah sledilo da , jer bi na osnovu a), b) i c) odmah sledilo da 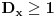 važi i za svako važi i za svako 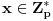 . .Budući da elemenata iz  , odnosno , odnosno  , ima sasvim dovoljno (za , ima sasvim dovoljno (za 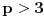 ), uvek možemo pronaći ), uvek možemo pronaći  i i 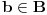 tako da ne bude tako da ne bude 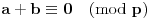 , pa na osnovu prethodne primedbe, važi i tvrđenje pod c). , pa na osnovu prethodne primedbe, važi i tvrđenje pod c). Tvrđenje 1. Ako je  bilo koji prost broj i bilo koji prost broj i  bilo koji ceo broj, onda, ako je bilo koji ceo broj, onda, ako je 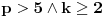 ili ili 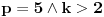 , za svako celo , za svako celo  , uzajamno prosto sa , uzajamno prosto sa  , postoje celi brojevi , postoje celi brojevi  , uzajamno prosti sa , uzajamno prosti sa  , za koje važi: , za koje važi: 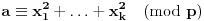 . .Dokaz. Neka je 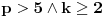 . Dovoljno je dokazati slučaj kada je . Dovoljno je dokazati slučaj kada je  , jer se slučaj , jer se slučaj 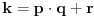 , za , za 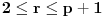 , i , i 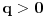 svodi na prethodni tako što uzmemo da svodi na prethodni tako što uzmemo da 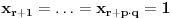 . .Broj  ima ima 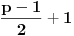 particija u particija u 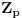 , tj. , tj. 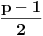 particija u particija u 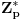 . Izaberimo zato bilo koju particiju, . Izaberimo zato bilo koju particiju, 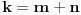 , gde je , gde je 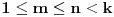 . Sada, za dato celo . Sada, za dato celo  , uzajamno prosto sa , uzajamno prosto sa  , uzmimo da je , uzmimo da je 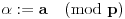 . .Budući da je 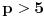 , na osnovu Leme 4, sledi da je , na osnovu Leme 4, sledi da je 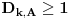 , , 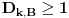 , , 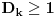 kao i kao i 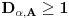 , , 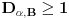 , , 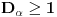 , pa odatle i na osnovu Leme 2, imamo da jednačina , pa odatle i na osnovu Leme 2, imamo da jednačina 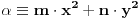 ima rešenja za neke ima rešenja za neke 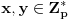 , bez obzira na to kom od skupova , bez obzira na to kom od skupova  ili ili  pripadali pripadali  i i  . .Sada možemo uzeti da je 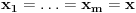 i i 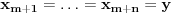 , pa je jasno da mora biti , pa je jasno da mora biti 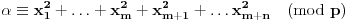 . .Ostao je još slučaj 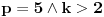 , koji je specifičan po tome što nije za svako , koji je specifičan po tome što nije za svako 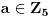 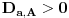 ni ni 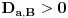 , pa ćemo zato koristiti činjenicu da za svako , pa ćemo zato koristiti činjenicu da za svako 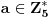 , jeste , jeste 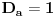 . .Na isti način kao i ranije, vidimo da je dovoljno dokazati tvrđenje u slučaju kad 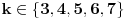 . .Ako 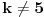 , onda se, zbog , onda se, zbog 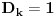 , broj , broj  može razložiti na zbir jednog kvadratnog i jednog ne-kvadratnog ostatka može razložiti na zbir jednog kvadratnog i jednog ne-kvadratnog ostatka 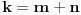 , (3=1+2, 4=1+3, 6=4+2, 7=4+3), pa vidimo da jednačina , (3=1+2, 4=1+3, 6=4+2, 7=4+3), pa vidimo da jednačina 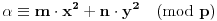 ima rešenja po ima rešenja po  i i  za svako za svako 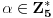 , tako da je, za dato celo , tako da je, za dato celo 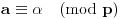 , dovoljno uzeti da je , dovoljno uzeti da je 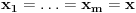 i i 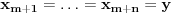 . .Ako je 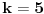 , imamo da je : , imamo da je : 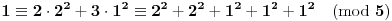 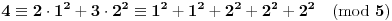 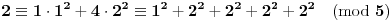 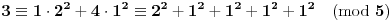 [Ovu poruku je menjao uranium dana 18.08.2005. u 03:50 GMT+1] [ Bojan Basic @ 25.08.2005. 22:03 ] @
Bio sam odsutan neko vreme pa sam tek sada stigao da malo detaljnije analiziram ovo tvoje rešenje i sve što mogu da kažem je svaka čast, zaista je odlično i nemam zamerki.
Ovu temu sam zapravo postavio da bih "promovisao" nešto što se zove Cauchy-Davenport inequality (Koši-Davenportova nejednakost) koja ume da bude veoma moćno sredstvo iako na prvi pogled ne izgleda tako. Formulacija same nejednakosti glasi ovako: Neka su 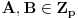 . Tada važi . Tada važi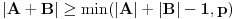 (Napomena: 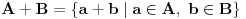 ) )Sada da vidimo kako se ovo može lepo iskoristiti u postavljenom zadatku. Neka je  skup svih kvadratnih ostataka po modulu skup svih kvadratnih ostataka po modulu  . Poznata je stvar da je . Poznata je stvar da je 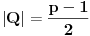 (koga interesuje dokaz može pogledati Lemu 1 u prethodnom postu), pa primenom navedene nejednakosti za (koga interesuje dokaz može pogledati Lemu 1 u prethodnom postu), pa primenom navedene nejednakosti za 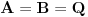 dobijamo dobijamo 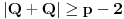 . Stavljajući sada . Stavljajući sada 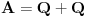 i i 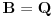 dalje sledi dalje sledi 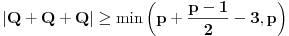 . Slučaj . Slučaj 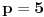 proveravamo direktno, dok za proveravamo direktno, dok za 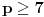 važi važi 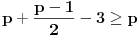 pa je pa je 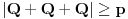 odnosno mora biti odnosno mora biti 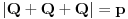 , iz čega očigledno sledi tvrđenje zadatka. , iz čega očigledno sledi tvrđenje zadatka.Možemo konstatovati još i to da se ova ideja u neznatno izmenjenom obliku može primeniti i za dokaz uopštenja koje je dao uranium. [Ovu poruku je menjao Bojan Basic dana 26.08.2005. u 19:05 GMT+1] [ uranium @ 26.08.2005. 16:25 ] @
Svaka čast!! Ovo je baš bilo moćno!
Dosad nisam ništa čitao od Aditivne teorije brojeva, ali sad kad si me već nagnao u tom pravcu Ako je od interesa, čisto da pomenem da je A.G.Vosper dokazao da u pomenutoj nejednakosti važi jednakost akko važi jedno od sledećih tvrđenja: 1. 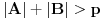 2. 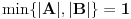 3. postoji 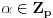 tako da je tako da je 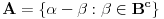 , gde je , gde je 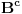 komplement skupa komplement skupa  u odnosu na u odnosu na 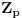 . .4. elementi skupova  i i  su aritmetički nizovi sa istom diferencijom (razlikom). su aritmetički nizovi sa istom diferencijom (razlikom).[ Bojan Basic @ 27.08.2005. 12:24 ] @
Nisam siguran na koji dokaz misliš pošto znam da ih ima više. Sećam se da se može isterati indukcijom po
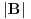 (i vrlo brzo se dođe do kraja) ali trenutno ne mogu da rekonstruišem kako tačno ide. U svakom slučaju, sad ću napisati jedan dokaz koji zaista koristi zanimljivu tehniku a nije previše dugačak tako da ne znam da li je to taj na koji si ti mislio. (i vrlo brzo se dođe do kraja) ali trenutno ne mogu da rekonstruišem kako tačno ide. U svakom slučaju, sad ću napisati jedan dokaz koji zaista koristi zanimljivu tehniku a nije previše dugačak tako da ne znam da li je to taj na koji si ti mislio.Prvo ćemo dokazati dve leme. Lema 1: Neka su  i i  neprazni podskupi nekog polja neprazni podskupi nekog polja  , i neka je , i neka je 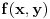 polinom stepena najviše polinom stepena najviše 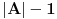 po po  i i 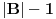 po po  takav da njegovi koeficijenti pripadaju polju takav da njegovi koeficijenti pripadaju polju  . Ako je . Ako je 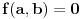 za svako za svako  i i 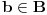 onda je onda je 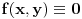 . .Dokaz: Možemo zapisati 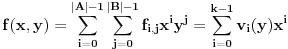 . Fiksirajmo sada . Fiksirajmo sada 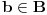 . Polinom . Polinom 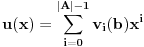 je stepena najviše je stepena najviše 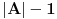 , ali s druge strane je , ali s druge strane je 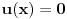 za sve za sve 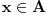 . Sledi da je . Sledi da je 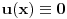 pa je i pa je i 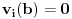 za svako za svako  . Međutim, kako je . Međutim, kako je  proizvoljno odabran element iz skupa proizvoljno odabran element iz skupa  , a kako je stepen polinoma , a kako je stepen polinoma 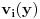 najviše najviše 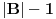 sledi da je i sledi da je i 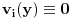 , a samim tim i , a samim tim i 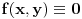 . .Lema 2: Neka je  konačan podskup polja konačan podskup polja  . Za svako . Za svako  postoji polinom postoji polinom 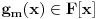 stepena najviše stepena najviše 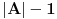 takav da je takav da je 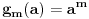 za svako za svako  . .Dokaz: Neka je 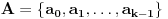 . Potrebno je pokazati da postoji polinom . Potrebno je pokazati da postoji polinom  takav da je takav da je 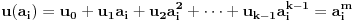 za za  . Primetimo da ovo zapravo predstavlja sistem od . Primetimo da ovo zapravo predstavlja sistem od  linearnih jednačina sa linearnih jednačina sa  nepoznatih, a znamo da takav sistem ima rešenje ako je njegova determinanta različita od nule. Determinanta ovog sistema je ništa drugo do Vandermondova determinanta nepoznatih, a znamo da takav sistem ima rešenje ako je njegova determinanta različita od nule. Determinanta ovog sistema je ništa drugo do Vandermondova determinanta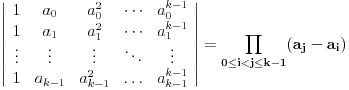 a ovo je očigledno različito od nule čime je dokaz leme završen. Dokaz: Neka je 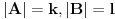 i i 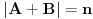 , i neka je , i neka je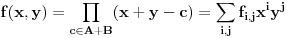 Primetimo da je 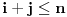 jer se u formiranom proizvodu nalazi tačno jer se u formiranom proizvodu nalazi tačno  članova. članova.Sada, na osnovu Leme 2, u polju 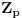 odaberimo polinome odaberimo polinome 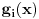 stepena manjeg od stepena manjeg od  i i 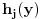 stepena manjeg od stepena manjeg od  takve da je takve da je 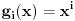 i i 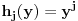 za sve za sve 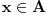 odnosno odnosno 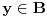 . Definišimo sledeći polinom: . Definišimo sledeći polinom: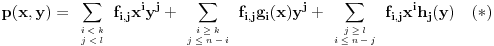 Primetimo da se za 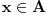 i i 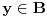 vrednosti polinoma vrednosti polinoma 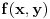 i i 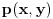 poklapaju. S druge strane, za tako odabrane poklapaju. S druge strane, za tako odabrane 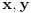 važi važi 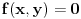 pa mora biti i pa mora biti i 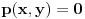 . Pošto je polinom . Pošto je polinom 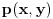 stepena manjeg od stepena manjeg od  po po  i stepena manjeg od i stepena manjeg od  po po  na osnovu Leme 1 sledi da mora biti na osnovu Leme 1 sledi da mora biti 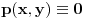 . Ako zapišemo . Ako zapišemo 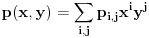 onda je onda je 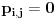 za svako za svako 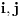 . .Ako je 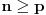 nejednakost koju dokazujemo je očigledna, pa uzmimo da je nejednakost koju dokazujemo je očigledna, pa uzmimo da je  . Potrebno je dokazati . Potrebno je dokazati 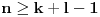 . Pretpostavimo suprotno, tj. . Pretpostavimo suprotno, tj. 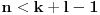 , odnosno , odnosno 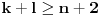 . U tom slučaju postoje brojevi . U tom slučaju postoje brojevi 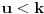 i i  takvi da je takvi da je 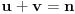 . Primetimo da se član . Primetimo da se član 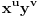 ne pojavljuje u drugoj i trećoj sumi izraza ne pojavljuje u drugoj i trećoj sumi izraza 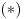 jer za jer za 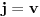 važi važi 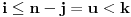 i slično za i slično za 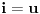 važi važi 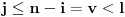 . Sledi da je . Sledi da je 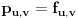 . Međutim, . Međutim, 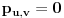 dok je dok je 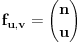 što za što za  ne može biti deljivo sa ne može biti deljivo sa  . Kontradikcija, čime je tvrđenje dokazano. . Kontradikcija, čime je tvrđenje dokazano.Pošto smo se toliko raspričali o ovoj nejednakosti red bi bio da vidimo još jednu njenu lepu primenu. Zadatak: Dokazati da se između datih 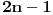 brojeva uvek mogu izabrati brojeva uvek mogu izabrati  takvih da je njihova suma deljiva sa takvih da je njihova suma deljiva sa  . .Rešenje: Posle, prvo malo probajte sami :) Toliko od mene za sada, imam još ponešto da kažem na ovu temu ali najpre malo pauze i da rešimo ovaj zadatak. [Ovu poruku je menjao Bojan Basic dana 13.09.2005. u 11:35 GMT+1] [ uranium @ 28.08.2005. 11:17 ] @
[ qzqzqz @ 06.10.2007. 11:42 ] @
Dovoljno pokazati datu teoremu za proste brojeve, jer ako je tacna za m,n onda je tacna i za mn, sto se lako dokazuje. Znaci imamo brojeve
 i pretpostavimo da je zbir brojeva u svakom podskupu ciji je broj elemenata p nije deljiv sa p, tj. da je uzajamno prost sa p. Izracunajmo vrednost zbira p-1 stepena svih zbirova elemenata podskupova od p elemenata. i pretpostavimo da je zbir brojeva u svakom podskupu ciji je broj elemenata p nije deljiv sa p, tj. da je uzajamno prost sa p. Izracunajmo vrednost zbira p-1 stepena svih zbirova elemenata podskupova od p elemenata. Kako je 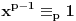 za (x,p)=1 to je data vrednost jednaka za (x,p)=1 to je data vrednost jednaka 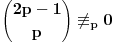 . .Sa druge strane dati broj je 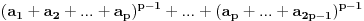 . Posmatrajmo koeficijent uz . Posmatrajmo koeficijent uz 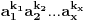 u datom broju ( u datom broju (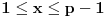 ), gde je ), gde je 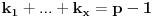 . Taj broj je jednak . Taj broj je jednak 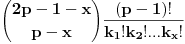 . Kako je . Kako je 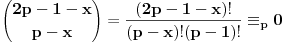 dobijamo kontradikciju. dobijamo kontradikciju.Secam se da sam negde video dokaz i preko Kosi-Davenportove teoreme, ali se ne secam kako ide. :) [ Bojan Basic @ 08.10.2007. 12:38 ] @
Dobro je rešenje, samo na kraju treba da posmatramo koeficijent uz
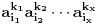 (tvoj zapis sasvim ignoriše članove u kojima se pojavljuje (tvoj zapis sasvim ignoriše članove u kojima se pojavljuje 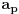 i brojevi s većim indeksom). i brojevi s većim indeksom).Evo kako bi išlo preko Koši—Davenportove nejednakosti. Poređamo 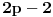 od datih brojeva (sve sem nekog izostavljenog broja od datih brojeva (sve sem nekog izostavljenog broja  ) redom u sledeću tabelu (posmatramo samo ostatke po modulu ) redom u sledeću tabelu (posmatramo samo ostatke po modulu  ): ):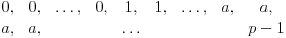 Ukoliko postoji kolona u kojoj su dva ista broja, taj broj očito se pojavljuje kao ostatak bar  puta (vrste imaju po puta (vrste imaju po 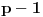 članova), pa je tvrđenje dokazano: uzmemo dotičnih članova), pa je tvrđenje dokazano: uzmemo dotičnih  brojeva. U suprotnom, po Koši—Davenportovoj nejednakosti (primenjenoj više puta) važi brojeva. U suprotnom, po Koši—Davenportovoj nejednakosti (primenjenoj više puta) važi  (gde su (gde su 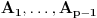 dvočlani skupovi — kolone gornje tabele). Dakle, svi ostaci su zastupljeni, pa postoji dvočlani skupovi — kolone gornje tabele). Dakle, svi ostaci su zastupljeni, pa postoji 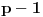 brojeva koji u zbiru daju ostatak brojeva koji u zbiru daju ostatak 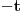 ; zajedno s brojem ; zajedno s brojem  činiće zbir deljiv sa činiće zbir deljiv sa  . .Lista ovdašnjih nerešenih zadataka sve se više prazni. [Ovu poruku je menjao Bojan Basic dana 08.10.2007. u 15:22 GMT+1] [ qzqzqz @ 10.10.2007. 19:40 ] @
Citat: Bojan Basic: Dobro je rešenje, samo na kraju treba da posmatramo koeficijent uz 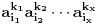 (tvoj zapis sasvim ignoriše članove u kojima se pojavljuje (tvoj zapis sasvim ignoriše članove u kojima se pojavljuje 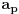 i brojevi s većim indeksom). i brojevi s većim indeksom).Pa isti je koeficijent, to je samo prenumeracija promenljivih. Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|