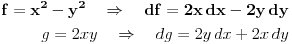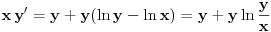[ proxyime @ 02.06.2005. 13:44 ] @
| Pozdrav moderatoru koji je izbrisao ovaj post... ma poceo sam ja rjesavati.. mucim se npr. evo prvi zadatak... ne mogu uopste otkriti kojom metodom da rijesim zadatak.. kod egzaktne diff vazi da je to ta jed. ako je df/dy=dg/dx a ja dobijem da je df/dy=-dg/dx tj. x^2 * y' - y^2 * y' - 2xy = 0 df=x^2-y^2 dg=- 2xy pa 2x =/= -2x i stvarono nemam pojma kako da rjesim ovaj problem... uradite mi samo jedan primjer ja cu pokusati ostale... p.s. mozda je u prvom postu izgledalo da nisam ni pokusao uraditi ali nije tako pozdrav slijedi prethodni post koji je bio izbrisan (//zadaci koje ne znam uraditi) Mole se svi koji znaju rijesiti ove zadatke da mi pomognu... nemam pojma o diff jednacinama a moram uraditi ove zadatke za semin...hvala svima koji pomognu ili bar pokusaju pomoci. //x^2 - x na kvadrat 1) x^2 * y' - y^2 * y' - 2xy = 0 2) 2x^3 * y' - y(2x^2 - y^2) 3) y' = (x^2 + 3y^2)/(2xy) 4) y' = e^(y/x) + y/x 5) y'' - 13y' + 42y = 84x + 16 - 2e^(6x) 6) x(x+2y)dx + (x^2-y^2)dy = 0 7) xy' - y - sqrt(x^2 + y^2) = 0 8) x^2 * y' + y = ax^2 * e(1/x) 9) xy' - y/(x+1) = x za y(1) = 0 10) y' - 2y/(x+1) - (x+1)^3 = 0 11) y'x + y*ln(x) = y + y*ln(y) hvala jos jedanput |