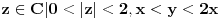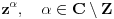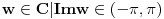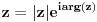[ akaret @ 03.06.2005. 15:28 ] @
| resavam neke zadatke iz matematika i pri tom sam naisao na neke specificne zadatke koje pojma nemam kako se resavaju, pa moze li neko da mi pomogne? 1.oblast D={z=x + iy ; 1<z<2, x<y<2x, x>0} preslikati funkcijom F(z)=lnz 2.oblast D={z=x + iy ; 1<x<2 , 0<y<2} preslikati funkcijom F(z)=1/z ako bi moglo i malo detaljnije hvala |