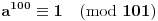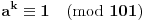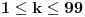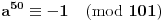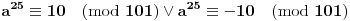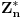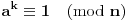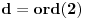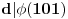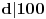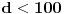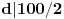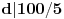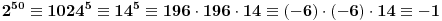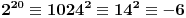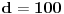Jel bi mogao da ponovis tacno text zadatka kako ide?

Jer, sta je red nekog celog broja? Beskonacno, osim ako nije 0 ili se ne radi o nekom elementu grupe, i to u odnosu na sabiranje. Ili mozda (svi invertibilni iz ), to je grupa u odnosu na ...

Kada kažem, "red" elementa u grupi mislim na prvi pozitivan ceo broj za koji
važi .

Dokazacemo da je red dvojke po modulu 101 bas 100.

neka je . Onda tj. . Ako je , onda ili . Ali:
(mod 101)
i
(mod 101),
pa mora biti

Da, to je sasvim korektan dokaz, i nemojte pogrešno da me shvatite, ali kada
već unapred znam da je red nekog elementa 100, isplati se potruditi se
oko računa i to pokazati. Da je ovaj dokaz počeo ispitivanjem npr. broja 5,
pokazalo bi se (nažalost ne baš brzo) da 5 nije onaj koga tražimo.
Nije teško zamisliti sličnu situaciju, u kojoj bi umesto 101 bio neki drugi značajno
veći prost broj i gde sistem nasumičnih pokušaja (verovatno) ne bi bio isplativ.

Dakle, bilo bi zgodno imati, ako ništa drugo, a ono bar neki uvid u to koje brojeve
ne bi trebalo testirati.

P.S. Srđane, stekao sam utisak da si (i) ti prvo pustio kompjuter da pronađe
najmanjeg "svedoka" a onda konstruisao dokaz, ako grešim izvini...

Mrzi me da pišem, ali imaš to na adresi

http://www.apfloat.org/prim.html

Znači, ako sam te dobro shvatio, Srđanov algoritam je najbolji postojeći?

S tim da treba ispitivati samo da li je stepen kanditata reda (p-1)/2q različit od 1 i -1, gde q prelazi preko svih prostih delitelja broja n. Takođe, svi brojevi tog oblika imaju svoj NZD, pa se kandidat prvo digne na taj stepen. Time se postižu neke uštede, ali to je to.