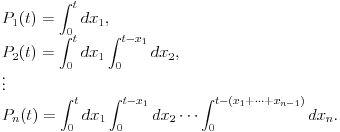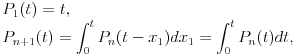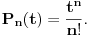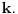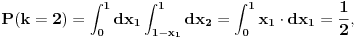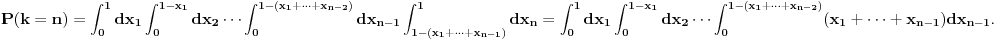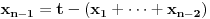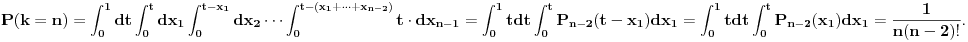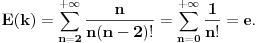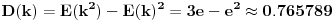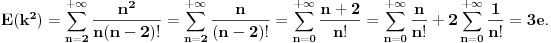[ vdivac @ 05.06.2005. 18:33 ] @
| U jednoj tehnickoj primeni (generisanje slucajnog vremena ponovnog pokusaja prenosa podataka ukoliko je linija za prenos koju deli vise uredjaja trenutno zauzeta) javio mi se jedan problem koji moze da se prevede u sledeci problem na jeziku verovatnoce: Izracunati matematicko ocekivanje koliko slucajnih brojeva uniformne (0,1) raspodele treba sabrati da bi se dobio zbir veci od 1? Probao sam sa programcicem sa 10.000 iteracija i dobio da procecno treba 2,752 brojeva, tako da sumnjam da je rezultat e. Da li ima nekog ovde kome je verovatnoca dovoljno sveza da moze ovo da mi dokaze (opovrgne)? Unapred hvala! |