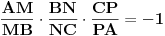[ Gn0m3 @ 06.06.2005. 20:01 ] @
| Zadatak s ispitnog roka na MATFu: Neka je ABC proizvoljan trougao i na njegovim stranicama se nalaze tachke P,M i N takve da vazhi: AM = 2MB BN = 2NC AC = 3CP Dokazati da su tachke P,M,N kolinearne. E sad ljudi koji su radili sabiranjem vektora(svi koje sam pitao) dobili su da su tachke kolinearne ali... ...ali... Menelajeva teorema glasi ovako : "Neka su M,N i P tri tachke koje se nalaze redom na stranicama AB, BC i AC. Tada su te tri tachke kolinearne ako i samo ako vazhi (AM \ MB) * (BN \ NC) * (AP \ PC) = -1." E sad u sledecem je trip : AC = AP + CP 3CP = AP + CP AP = -4PC Time dobijamo sledece : (AM \ MB) * (BN \ NC) * (AP \ PC) = -1 ((2MB) \ MB) * ((2NC) \ NC) * ((-4PC) \ PC) = -1 2 * 2 * (-4) = -1 -16 = -1 shto je ochigledno nemoguce!!! U chemu je fora??? |