Cassey je dokazao ovo ali je njegov dokaz nažalost izgubljen prilikom kraha baze. Svejedno, dokazaću opštije tvrđenje.

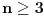
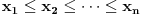
Za svako i niz pozitivnih realnih brojeva važi sledeća nejednakost:


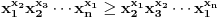
Dokazujemo inducijom po .

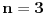
Za treba dokazati

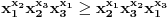
Logaritmujući dobijamo da je ova nejednakost ekvivalentna sa

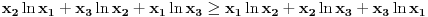
odnosno

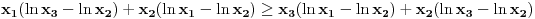
što se može zapisati kao

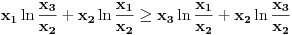
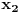
Deljenjem sa vidimo da je ovo ekvivalentno sa

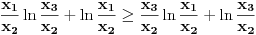
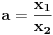
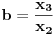
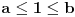
Uvedimo smene , . Očigledno je . Nejednakost se svodi na

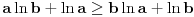
što je ekvivalentno sa

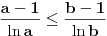
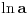
(znak se promenio jer je negativno).
Posmatrajmo funkciju

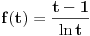
Prvi izvod te funkcije je

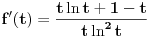
Imenilac ovog razlomka je očigledno pozitivan. Predstavimo brojilac kao funkciju

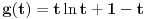
Prvi i drugi izvod su


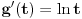
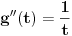
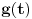
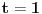
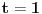
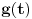
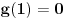
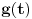
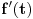
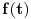
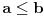
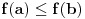
Funkcija ima u tački prvi izvod jednak , a pošto je drugi izvod pozitivan sledi da u tački funkcija ima minimum. Pošto je zaključujemo da je funkcija nenegativna, a samim tim je i nenegativna, pa je funkcija rastuća. Pošto je sledi da je i , čime je baza indukcije dokazana.

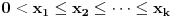
Pretpostavimo sada da tvrđenje važi za niz od brojeva, tj. da za važi

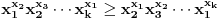
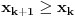
Za na osnovu baze indukcije imamo

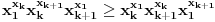
Množeći ove dve relacije dobijamo

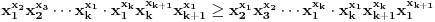
iz čega sledi

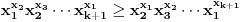
Ovim je dokaz završen.

Polazni zadatak očigledno je specijalan slučaj dokazanog tvrđenja za .

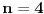
Evo i moje verzije (ovo je samo copy/paste iz moje knjizice uz male izmene i nisam proveravao ispravnost, pa me upozorite ako ima gresaka):

Ako je funkcija konkavna na intervalu , a i () brojevi iz tog intervala, onda je: Zaista, ako je , jasno je da vazi jednakost. Pretpostavimo da je . Prema definiciji konkavnosti, nejednakost
vazi za svaka dva broja , . Za i ova nejednakost postaje: Odatle sledi (1). Logaritamska funkcija je konkavna na intervalu . Zato za brojeve , i koji zadovoljavaju nejednakosti vazi: Jednostavnim transformacijama dobijamo nejednakost . Sledi da je . Ako brojeve i zamenimo sa i , odnosno i , dobicemo nejednakosti i . Njihovim mnozenjem dobija se da je , odakle sledi:

Dobro je, samo nisam razumeo kakvu knjižicu pominješ (hoćeš da kažeš da pišeš knjigu ili sam ja pogrešno rastumačio :)? Je li dokaz tvoj originalan?

Dokaz nije moj, vec sam ga nasao u longlistu iz godine kada je Beograd bio domacin Olimpijade. A sto se tice moje knjizice, u nju stavljam najinteresantnije zadatke, teoreme i slicne stvari, ali samo one koje se ne nalaze u nekim od knjiga koje posedujem. Uglavnom su to stvarcice sa ES-a, iz nekih casopisa, interneta i slicno (tek da imam sve to na jednom mestu). Tek sam poceo da je pisem, pa ima samo oko 40 strana, ali ce vrlo brzo biti dopunjena sa puno informacija. Mogu ti poslati source, ili PDF ako te interesuje.