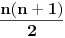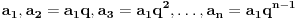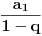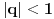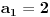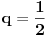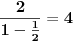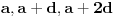[ rakakrone @ 12.06.2005. 12:51 ] @
| Da li mi neko moze reci kako da resim ove zadatke? 1. Odrediti zbir prvih 106 članova niza prirodnih brojeva? 2. Odrediti zbir članova beskonačnog niza 2,1,1/2,1/4... 3. Zbir tri uzastopna člana aritmetičkog niza je 27. Ako je najveći od njih dva puta veći od najmanjeg, dokazati da je proizvod tri broja 648. |