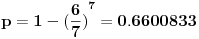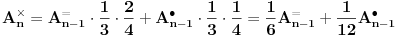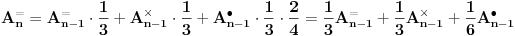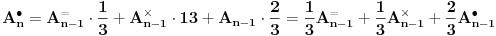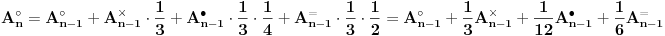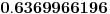Nisam bas skontao u kojim smerovima mogu da ih okrecem?

Istok sever zapad jug ili kako?

Ako cilindar stoji vertikalno (npr.) onda se vrata otvaraju kada su sve četiri glave okrenute na dole ili sva četiri repa okrenuta na dole. Znači, kada ti izvadiš dve ribe nekima je glava okrenute dole a nekima rep, i to izokrećeš kako hoćeš pa vratiš nazad.

Susjedne pregrade pa nasuprotne...neću dalje.
Čestitam Bojanu na plasmanu za olimpijadu.Naspavaj se i ne
pij piva,pa će biti i solidan plasman tamo.

Da li cilindar može da se zavrti a da zatvorenik ne vrati ribu u njega?

Ne može.

Dobro, onda ćemo ovako: Zatvorenik može da izvadi jednu ili dve ribe. Da bi to uradio, on svakako mora da ih napipa i uzme u ruku. Recimo da ne vadi odmah ribe, nego da ih prvo sve četiri dobro opipa (otkrije gde je kojoj glava, a gde rep) i ustanovi kako su okrenute. Tri su mogućnosti:
1. Sve četiri ribe su okrenute na istu stranu (mora da se zatvorenik baš zaneo pipanjem riba kad nije primetio da su se vrata već otvorila). Zatvorenik može da izađe.
2. Jedna riba je okrenuta u suprotnom pravcu od ostale tri. Zatvorenik vadi tu ribu, okreće je i vraća u cilindar. Vrata se otvaraju i može da izađe.
3. Dve ribe su okrenute u suprotnom pravcu od ostale dve. Zatvorenik vadi te dve ribe, okreće ih i vraća u cilindar. Vrata se otvaraju i može da izađe.

_{[Ovu poruku je menjao Milan Jovanovic dana 09.10.2005. u 23:36 GMT+1]}

Nisam siguran da li se šališ ili ne, ali u svakom slučaju ne ide tako. Zatvorenik ne može prvo da ispipa ribe da proveri kako su okrenute. Ako baš tražiš precizan "model" zamisli da cilindar ima četvoro vrata (za svaku ribu po jedna) i da on može da otvori dvoja vrata, izvadi ribe, izokreće ih, vrati, pa sve ispočetka (naravno posle okretanja cilindra).

Jel cilindar (ako mu je osa normalna na pod) podijeljen ravnima paralelnim sa podom? Ako si izvadio ribe iz cilindra, okrenuo ih u istom smjeru i vratio u cilindar jel poslije vrtenja cilindra te dvije ribe ostaju u istom smjeru? Jel ribe "leze" na ravnima koje su paralelne podu? Jel ribe mogu da budu okrenute u 2 suprotna smijera ili u vise? Ako je to slucaj (mada nevjerujem) onda izvadis ribe iz 3 i 4 pregrade, onu iz trece okrenes kao onu iz cetvrte i vratis, poslije vrtenja izvadis ribe iz 2 i 3 pregrade i onu iz druge okrenes kao sto je okrenuta ona iz trece, nakon vrtenja cilindra izvadis ribe iz prve i druge pregrade i onu iz prve okrenes kao onu iz druge i tada su sve cetiri ribe u istom smijeru.

Ne, već dvema međusobno normalnim ravnima koje su normalne i na pod.

Da.

Jok. "Osa" ribe (recimo kičma :)) je normalna na pod.

Samo dva smera.

Ne može ovako jer kad se cilindar zavrti (vrti se oko svoje ose) onda više ne znaš koja je koja pregrada (to i jeste poenta vrtenja).

_{[Ovu poruku je menjao Bojan Basic dana 10.10.2005. u 02:02 GMT+1]}

Ako vidimo ribe kako izgledaju kad ih izvučemo
onda je lako napraviti da imamo tri ribe sa glavama
gore.
Onda bez veze izvučemo jednu i okrenemo je kontra.
Sad imamo barem 2:2.Ali ne znamo da li su iste u susjedstvu
ili kontra.
Pa probamo dvije kontra.Ako su iste...
Ako nisu onda znamo da nisu.
A sad uzmemo dvije susjedne,pa ako su iste onda...
A ako nisu onda moram još razmišljati.E ova dva zadnja poteza
ću pokušati riješiti kasnije.Umorio sam se.
Ili neka neko nastavi!

A mogu li se pregrade nekako obeleziti? :-)

Ili mozda ribe?? :))

_{[Ovu poruku je menjao mida5 dana 11.10.2005. u 00:35 GMT+1]}

Može li ovako:

sa x ću označiti ribe čiju poziciju ne znamo
x x
x x

Uzmemo ribe "preko puta" i obje ih okrenemo glavom na gore, i onda je
g x
x g
Uzmemo jednu ribu ofrlje, i ako je glava gore, uzmemo ribu, u pregradi lijevo, i ako ona nije već nagore, okrenemo je i onda je
g x
g g
Ako se vrata ne otvore, onda uzimamo po dvije ribe jedna kraj druge, dok ne izvučemo jednu sa glavom nadole.

Jesam li blizu?

Ne!Prešao si samo trećinu puta.
Ako pročitaš moju prethodnu poruku imaš rješenje
za još jednu trećinu puta.

_{[Ovu poruku je menjao zzzz dana 12.10.2005. u 23:53 GMT+1]}

Skont'o

Već sam pojasnio kako da dobijemo

gx
gg
i onda je x sigurno d (osim ako se vrata ne otvore) i imamo četiri mogućnosti
gd dg gg gg
gg gg dg gd
Onda uzmemo ribu u gornjem lijevom ćošku i ribu nasuprot. Ako je jedna glavom na dole, samo je okrenemo, a ako nije, onda ribu u gornjem lijevom ćošku obrnemo, a ovu drugu samo vratimo.
dd gg dg gg
gg gg dg gg
U dva slučaja se vrata otvaraju, a u druga dva uzmemo dvije ribe jedna kraj druge i ako su iste okrenemo ih, a ako nisu opet ih okrenemo :) i dobićemo dvije ribe različitog položaja jedna nasuprot druge, i onda samo izvučemo dvije ribe da su jedna naspram druge i okrenemo ih.


_{[Ovu poruku je menjao 3125 dana 13.10.2005. u 12:21 GMT+1]}

Ima ovdje jedna radosna vijest,a jedna tužna.
Ispravno si skontao do šestog sprata.Svaka čast,čestitam.
Tužna vijest je:ulaz je krivi.Treba saći dole pa ispočetka do sedmog.
Onaj robijaš kad okreće ribu pojma nema šta je gore,a šta dole.
To ti je neki čekljun koji on može zarotirati samo za pola kruga
i gotovo.Nema pojma gdje je glava a gdje rep.
******************************************
E sad ovo je lako riješiti kad je ono prvo rješeno.Bojan je sudija
pa će na kraju reći da li je dobro rješenje.
******************************************
A ja kažem:Ovaj zadatak ima svoj rep.Čim ga neko riješi napisaću
taj rep.

Zbog simetrije postoje 8 (grupa) stanja u kojima se cilindar moze naci:

aa bb ab ab ab ba aa aa
aa aa ba aa ab aa ba ab

a i b su nepoznate.

neka se cilindar posmatra tako da odeljci budu (na crtezu):

gore levo gore desno
dole levo dole desno


Neka je pocetna pozicija

xx
xx

1. dole levo, gore desno (na crtezu) postaviti u istom smeru
posle rotacije moguca stanja, (izuzev ciljnog) su

ba ab ba aa aa
ab aa aa ba ab

2. uzmimo gore levo, dole levo. Ako su ribe istog smera onda ih vratimo kako su i bile;
ako su ribe razlicitog smera onda ih okrenimo tako da budu istog smera i dobijamo skup mogucih stanja

ab ba aa aa
aa aa ba ab

3.uzmimo gore levo, dole levo. Ako su ribe istog smera onda jednu okrenimo da budu razlicitog smera;
ako su ribe razlicitog smera onda ih okrenimo tako da budu istog smera i dobijamo skup mogucih stanja

ab aa ab
ba bb ab

4. uzmimo gore levo, dole desno ako su obe istog smera obe okrenimo i kraj;
ako su razlicite onda ih vratimo kako su bile i dobijamo skup mogucih resenja

aa ab
bb ab

5. uzmimo levo dole, levo gore ako su istog smera obe okrenimo i kraj;
ako su razlicitog obe okrenimo i dobijamo

ba
ab

6. uzmimo gore levo,dole desno obe okrenimo i kraj.

resenje u 6 poteza


_{[Ovu poruku je menjao Cybernoid II dana 15.10.2005. u 10:35 GMT+1]}

A i ti si koristio ovo da zatvorenik gleda u kakvom je položaju riba. Plus što je moje rješenje u 0-5 poteza, a tvoje 0-6

Skontao sam opet, samo je malo duže.


Na početku imamo ovo

gd dg gd dg dd gg dg gd gg gg gd dg dd dd
dg dg gd gd gg dd gg gg dg gd dd dd dg gd

Onda okrenemo ribu dole lijevo
gd dg gd dg dd gg dg gd gg gg gd dg dd dd
gg gg dd dd dg gd dg dg gg dd gd gd gg dd

Kad sredimo imamo ovo

gd dg gg gg gd gd dd dd dd dg gg gd gd dg
gg gg dg gd dd dd gd dg gg dg dd gd dg gd

Onda okrenemo ribu gore desno
gg dd gd gd gg gg dg dg dg dd gd gg gg dd
gg gg dg gd dd dd gd dg gg dg dd gd dg gd

Pa kad sredimo imamo ovo
dd dg gd gg gd dg dg gd gd dg gg dd gg dd
gg dg gd dd dg gd gg dd gg dd dg gd gd dg

Pa okrenemo ribe gore lijevo i gore desno (ne između sebe)
gg gd dg gg dg gd gd dg dg gd dd gg dd gg
gg dg gd dd dg gd gg gg gg dd dg gd gd dg

Pa kad sredimo imamo ovo :)
gd dg gg gd dd dg gd dg gg gg dg gd dd dd
dg gd dd gd gg dg gg gg dg gd dd dd gd dg

Sad okrenemo ribe po dijagonali
dd gg dg dd gd gg dd gg dg dg gg dd gd gd
dd gg dg gg gd dd gd gd dd gg dg dg gg dd

Pa kad sredimo imamo ovo
dg dd gd gg dd gg dg dg gg dd gd gd
dg gg gd dd gd gd dd gg dg dg gg dd

Sad okrenemo ribe gore lijevo i dole lijevo (ne između sebe)
gg gd dd dg gd dg gg gg dg gd dd dd
gg dg dd gd dg dd gd dg gg gg dg gd

Pa kad sredimo imamo ovo
gd dg dd gg dg dg gg dd gd gd
dg gd gd gd dd gg dg dg gg dd

Sad okrenemo ribe po dijagonali
dd gg gd dg gg gg dg gd dd dd
dd gg gg gg dg gd dd dd gd dg

Pa okrenemo ribu gore lijevo
dd gg dg dg gg dd gd gd
gg gg dg gd dd dd gd dg

Pa kad sredimo imamo ovo
gd dg dg dd gg gd
dg gd dg gg dd gd

Sad okrenemo ribe po dijagonali
dd gg gg gd dg dd
dd gg dd gd dg gg

Sad okrenemo ribe gore lijevo i gore desno
gg dd dg gd
gg dd gd dg

Sad ih okrenemo po dijagonali
gg gg
gg gg

Valjda nema grešaka.

Znači treba okrenuti ribu gore lijevo, pa kad se zavrti okrenuti ribu gore desno, pa kad se zavrtti okrenuti ribe gore desno i gore lijevo, pa po dijagonali, pa gore lijevo i dole lijevo, pa opet po dijagonali, pa ribu gore lijevo, pa po dijagonali, pa gore lijevo i gore desno, pa opet po dijagonali, i izaći će prije ili kasnije

_{[Ovu poruku je menjao 3125 dana 15.10.2005. u 22:14 GMT+1]}

3125 je shvatio smisao zadatka.Ali način
njegove analize je katastrofa.
cybernoid nije pročitao prethodne diskusije.

Možda i ja griješim.Ali evo kako ja to gledam:
-Ako je brava zaključana onda je sitiucija 2:2 ili
3:1.Trećeg nema jer 4:0 otključava.
-Pretpostavim da je 2:2.Tu imamo samo dvije
mogućnosti.Ili su isti susjedni,ili nasuprot.
--Prvi potez (logično) okrećemo dvije suprotne.
Time ne remetimo 2:2 ako ne otključamo.(A onda
su izgleda isti susjedni,nisam ni to poremetio?.)
--Drugi potez(logično) okrećemo dvije susjedne.
Time ne remetimo 2:2 ako ne otključam,ali ih
pretvaramo u suprotne.
--Treći potez(logično) okrećemo dvije suprotne.
Time ne remetim 2:2 ako ne otključam.
Ako ne otklučamo onda je moja pretpostavka 2:2
pogrešna.Šta sad da se radi?Kako da tih prokletih
3:1 pretvorim u 2:2 ?Kad bih to znao onda bih lako
ponovio prethodni postupak.

Sjetiću se ja čim malo odspavam!

Kratko:
1)Okrenem dvije suprotne.
2)Okrenem dvije susjedne.
3)Okrenem dvije suprotne.
4) --e ovdje sam se zbunio,ali mi izgleda kao da bi
tri sledeća poteza ličila na ona prva tri.

Nebi rekao da to valja, jer imaš i osam kombinacija 3:1, pa će se i one pomješati, a ovo moje je "samo" 10 poteza:
1.Okrenemo ribu dole lijevo
2.Okrenemo ribu gore desno
3.Okrenemo ribe gore desno i gore lijevo
4.Okrenemo ribe po dijagonali
5.Okrenemo ribe gore lijevo i dole lijevo
6.Okrenemo ribe po dijagonali
7.Okrenemo ribu gore lijevo
8.Okrenemo ribe po dijagonali
9.Okrenemo ribe gore lijevo i gore desno
10.Okrenemo ribe po dijagonali

cek, zatvorenik ne moze da vidi ni ribe koje je izvadio ?

Tako kaže zzzz

zzzz
zatvorenik moze da uporedi medjusobnu orjentaciju riba.
http://www.elitesecurity.org/poruka/912361
zatvorenik ne zna orjentaciju izvadjenih riba u odnosu na pod.
http://www.elitesecurity.org/poruka/917069
pogresno sam shvatio da su oba uslova zadata, a ne da su to postavke dva razlicita zadatka.

Ako zatvorenik ne moze da utvrdi da li su dve izvadjene ribe isto okrenute ili ne, onda:

1. start



ab aa ab ab ba

ab bb ba aa aa



rezultat



aa ab aa aa bb

bb ab aa ba ba



2. pre



aa ab ab ba

bb ab aa aa



posle



aa ab ab ba

aa ba bb bb





3. pre



ab ab ba

ba aa aa



posle



aa aa bb

aa ba ba



4. pre



ab ba

aa aa



posle



ab ba

ba ba



5. pre



ab aa ab

ba bb ab



posle



aa ab aa 

aa ab bb



6. pre



aa ab

bb ab



posle



aa ab

aa ba



7. pre 



ab

ba



posle



aa

aa

_{[Ovu poruku je menjao Cybernoid II dana 18.10.2005. u 13:23 GMT+1]}

Bojan je napisao:Zatvorenik ne može da vidi ribe, međutim može da izvadi dve proizvoljne ribe, okrene ih ako želi (može i da okrene samo jednu) i vrati nazad, i to može da uradi neograničen broj puta...

Nije baš jasno vidi li kako stoji riba pošto je izvuče.Ja tvrdim da je zadatak rješiv
i ako ih ne vidi.Najduže u sedam poteza.(Jedan potez je okretanje dvije ribe ili
okretanje samo jedne.)
Evo tih okretanja:
1)Dvije suprotne.
2)Dvije susjedne.
3)Dvije suprotne.
4)Jednu (bilo koju).
5)Dvije suprotne.
6)Dvije susjedne.
7)Dvije suprotne.
Brava će se sigurno otvoriti ma kakva početna kombinacija bila.U najgorem slučaju
u sedmom potezu.

Da li se brava zavrti između ova dva poteza?Ako je odgovor NE,onda su 1) i 2)
jedan potez.Potezi 5) i 6) su nepotrebni.
Nemamo osam kombinacija „3:1“ već samo jednu.Sve one ostale nastaju rotacijom
ili zrcalnim preslikavanjem jedne.Kad bi rotirao za neki manji ugao od pravog imao bi ih koliko hoćeš.
Imamo samo četiri kombinacije.
-a)Sve ribe okrenute na istu stranu.-b)Jedna nasuprot druge tri.-c)Dvije i dvije nasuprot i susjedne.-d)Dvije nasuprot dvije ali unakrst.
Ako je ova poslednja rješavam se zatvora prvim potezom.
Ako je -c) onda ću se riješiti drugim potezom,ili napraviti –d) pa riješiti trećim.
Ako ni to ne prođe onda je to slučaj –b).Tada u četvrtom potezu okrenem samo
jednu ribu.Ili sam otključao ili napravio kombinaciju –c) ili -d).
A tada su mi potezi 5,6 i 7 isti kao 1,2 i 3.
Naravno da ću na početku provjeriti da nije slučajno odmah bila –a).

Ja sam skonto da ne može da ih vidi dok ih ne izvuče, a da ih vidi kad ih izvuče

Cybernoid ll ima ispravnu taktiku.Samo mi nije
jasno,ako već nije reducirao kombinacije na 4
osnovne,zašto ih nije prikazao sve?

Postavlja se ovakvo pitanje:
Ako zatvorenik ne razmišlja već ide na sreću,
pa sa podjednakom učestalošću okreće nekad
jednu,nekad dvije susjedne,a nekad dvije nasuprotne.
Kolike su mu šanse da u sedam poteza pogodi?
Računamo da na startu nije bila brava otključana.

mislim da sam vec napisao usled simetrije u odnosu na "nebitno gore ili dole" ima 8 elemenata.
Grupa kombinacija u odnosu na operaciju "zavrtimo cilindar i prevrnimo jednu ili dve ribe" ima 6 elemenata (usled simetrije).



_{[Ovu poruku je menjao Cybernoid II dana 18.10.2005. u 13:40 GMT+1]}

Mene zbunjuje onih 5 kombinacia u "1.start"
Druga je rotacija prve u desno za 90 stepeni.
Peta je rotacija četvrte u lijevo za 90 stepeni.

Pa onda odluka da ideš dijagonalno okrenuti
dvije ribe bez nekog objašnjenja.

Ajde dobro,svi su riješili.Mene zanima onaj dodatak
sa nasumičnim probama.Po meni šansa je oko 2/3.

Nisam ja nikakav sudija, ja samo ponekad postavim zadatak a dalje ga svi zajedno rešavamo i diskutujemo. Sa ovim zadatkom problem je bio što zaista nisam objasnio da li zatvorenik vidi ribe kada ih izvadi ili ne, a nažalost ja sam bio izgubio link na kom sam video zadatak pa nisam mogao da se javim i preciziram (to je bio i razlog što se nisam pojavljivao na temi). U međuvremenu sam našao originalnu postavku u kojoj se može pročitati da zatvorenik zaista može da vidi ribe kada ih izvadi, ali u svakom slučaju još je bolje što su rešene obe verzije.

E sad da se osvrnemo na zzzz-ovo pitanje. Ja sam na brzinu isprogramirao neku simulaciju koja je u nekoliko puštanja sa milion uzoraka dala sledeće uspešnosti:

pa deluje da je zzzz-ova procena 2/3 vrlo blizu istine, ali nažalost trenutno ne vidim kako bi se ovo moglo dokazati.

Vjerovatnost da se nasumice otključa brava iz sedam pokušaja je:


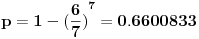
Ako imamo 16 mogućih kombinacija,pa odbacimo one dvije gdje su
Sve ribe gore ili dole,ostaje 14.Od njih 14 imamo 8 gdje je jedna
riba kontra tri ostale.Imamo 4, gdje su dvije gore a dvije dole,ali su
susjedne.
Imamo i dvije gdje su dvije i dvije nasuprotne okrenute na istu
Stranu.
Ako je u startu prvi slučaj : p(1)= 8/14 * 1/3 * ¼=1/3*1/7.
Pa onda p(2)=4/14 * 1/3 * 1/2 i p(3)= 2/14 * 1/3 * 1
p=p(1)+p(2)+p(3)= 1/7
.Šansa da odmah pogodi je 1/7 bez obzira koja početna
kombinacija bila.Vrijedi i za drugu rundu.
Odatle ide da je šansa da ne pogodi iz prve 6/7.
A iz sedam puta, sedmostruki umnožak.

Ispade da je Bojan nešto pogriješio u svom programu
"Monte karlo".

Problem je bio u tome što smo različito interpetirali ovo nasumično okretanje. U tvojoj varijanti, koliko vidim, prvo biraš "tip" okretanja (da li jednu ribu, dve susedne, ili dve naspramne) pa onda dodatno biraš šta se tačno radi sa tim tipom. U mom slučaju postoji ukupno 10 mogućnosti (4 puta po jedna riba, ili neki od 6 parova) i svaku mogućnost računam podjednako verovatno. Druga stvar gde nam se razlikuju shvatanja je to što si ti odbacio dve spasonosne kombinacije pa ti preostaje 14, a u mom slučaju ništa ne odbacujem već ako se slučajno desi da se ribe nađu u tom položaju onda blago njemu - oslobođen je pre prvog poteza. Nema veze, prihvatićemo tvoje tumačenje jer si ti formulisao pitanje na koje tražimo odgovor. E sad, šta mene brine kod ovog tvog rešenja - mislim da ne možeš tek tako da ovu verovatnoću 6/7 provučeš kroz sve naredne krugove jer ti niko ne garantuje da određena vrsta kombinacije ima podjednaku verovatnoću kao i u prvom krugu. Ja imam neku ideju kako ovo korigovati ali ne mogu sad da je razrađujem jer sam umoran, potrudiću se da sutra dovršim.

Bio sam u pravu u vezi sa ovim što sam rekao u prošloj poruci, sada imam kompletno rešenje. Pre toga ću napisati rezultate simulacije ispravljene prema objašnjenju koje je dao zzzz (nekoliko puštanja sa uzorkom milion):


Moja ideja je da sastavimo rekurentne relacije koje računaju verovatnoću da se pojavi određena kombinacija u određenom potezu. Te relacije su sledeće:




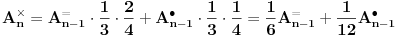
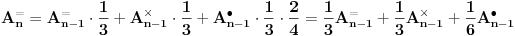
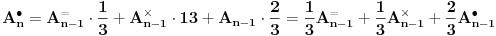
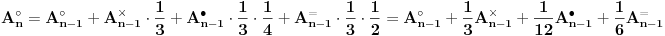
Pri tome oznake na levim stranama jednakosti označavaju, redom, poziciju sa jednake po dve naspramne ribe, po dve susedne ribe, jedna riba različita od tri, i sve četiri jednake. Rešavanjem sistema dobijamo sledeću tablicu



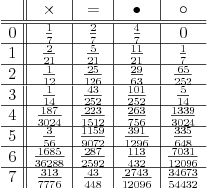
Nas zanima poslednji broj, čija približna vrednost je 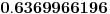, i možemo zapaziti da odgovara empirijskim rezultatima.