|
|
[ cassey @ 14.06.2005. 01:27 ] @
|
| Evo sredjivao sam nesto komp, pa reko da postavi (za sad nejednskosti)... Mozda nekom koristi... (koliko sam ja dobar :-)
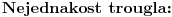 Za proizvoljne realne brojeve Za proizvoljne realne brojeve 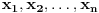 vazi: vazi:
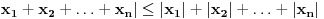
 Za Za 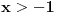 i i 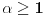 vazi vazi
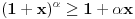 . .
 Za realne brojeve Za realne brojeve 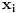 i i 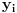 , , 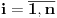 vazi: vazi:
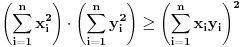
Jednakost vazi akko 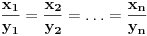 . .
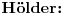 Ako za pozitivne brojeve Ako za pozitivne brojeve 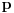 i i 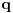 vazi vazi 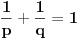 , tada za svaki par , tada za svaki par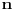 -torki realnih brojeva -torki realnih brojeva 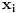 i i 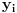 vazi: vazi:
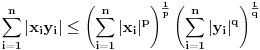
Jednakost vazi akko 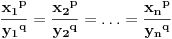 . .
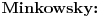 Neka je Neka je 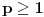 i i 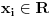 i i 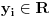 za za 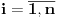 . Tada vazi: . Tada vazi:
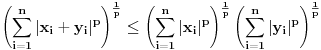
Jednakost vazi akko 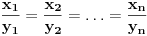 . .
 Ako je funkcija Ako je funkcija 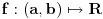 konveksna i konveksna i 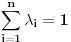 , , 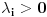 i i 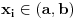 tada vazi: tada vazi:
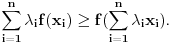
Funkcija 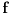 je konveksna na intervalu je konveksna na intervalu 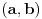 ako za svako par brojeva ako za svako par brojeva 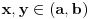 vazi vazi 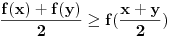 , sto je ekvivalentno sa uslovom , sto je ekvivalentno sa uslovom 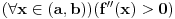 . Ako je funkcija . Ako je funkcija 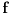 strogo konveksna, tada jednakost vazi akko su svi strogo konveksna, tada jednakost vazi akko su svi 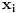 medjusobno jednaki ili su svi medjusobno jednaki ili su svi 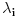 sem jednog jednaki sem jednog jednaki 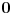 . .
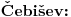 Ukoliko realni brojevi Ukoliko realni brojevi 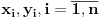 zadovoljavaju uslov: zadovoljavaju uslov: 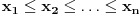 i i 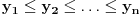 tada vazi: tada vazi:
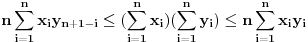
Jednakost vazi akko 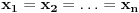 ili ili 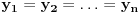 . .
 Neka je za Neka je za 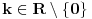 , sredina , sredina 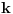 -tog reda: -tog reda:
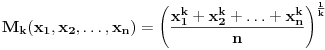
 rastuca funkcija po rastuca funkcija po  , odnosno , odnosno 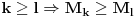 . Specijalno . Specijalno 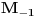 je harmonijska, je harmonijska, 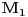 je aritmeticka, je aritmeticka, 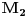 kvadratna, a kvadratna, a 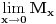 geometrijska sredina brojeva geometrijska sredina brojeva 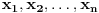 . Zbog toga vazi nejednakost medju sredinama . Zbog toga vazi nejednakost medju sredinama 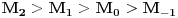 . .
Jednakost vazi akko 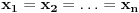 . .
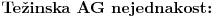 Za pozitivne brojeve Za pozitivne brojeve 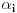 za koje va\v zi za koje va\v zi 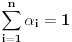 , nejednakost izmedju aritmeticke i geometrijske sredine glasi: , nejednakost izmedju aritmeticke i geometrijske sredine glasi:
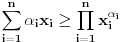
Jednakost vazi akko su svi 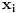 medjusobno jednaki ili su svi medjusobno jednaki ili su svi 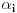 sem jednog jednaki sem jednog jednaki 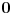 . .
 Za niz realnih brojeva Za niz realnih brojeva 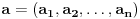 Definise se funkcija Definise se funkcija 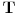 sa sa 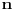 promenljivih: promenljivih:
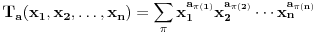
gde se sumiranje vrsi po svim permutacijama 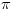 skupa skupa 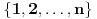 . Ukoliko za dva niza realnih brojeva . Ukoliko za dva niza realnih brojeva 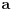 i i 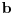 vazi: vazi: 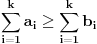 za za 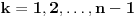 i i 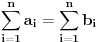 , tada vazi za sve , tada vazi za sve 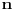 -torke nenegativnih brojeva i nejednakost: -torke nenegativnih brojeva i nejednakost:
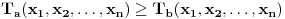
Jednakost vazi akko su 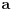 i i 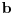 identicni ili kada je identicni ili kada je 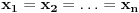 . .
 Za nenegativne realne brojeve Za nenegativne realne brojeve 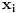 , , 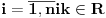 vazi: vazi:
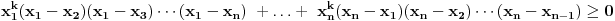
Jednakost vazi akko je 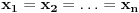 . .
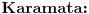 Niz Niz 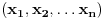 majorira niz majorira niz 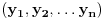 ako vazi ako vazi 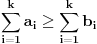 za za 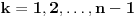 i i 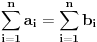 . To je neophodan i dovoljan uslov da za svaku konveksnu funkciju vazi: . To je neophodan i dovoljan uslov da za svaku konveksnu funkciju vazi:
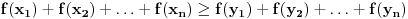
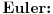 Za nizove realnih brojeva Za nizove realnih brojeva 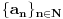 i i 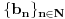 definisane sa definisane sa 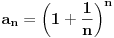 i i 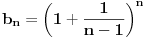 vazi: vazi:
 |
[ Nedeljko @ 14.06.2005. 10:56 ] @
Jedna mala ispravka:
Citat: cassey: [Funkcija 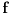 je konveksna na intervalu 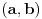 ako za svako par brojeva 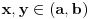 vazi 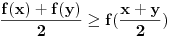 , sto je ekvivalentno sa uslovom 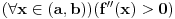 .
Ako je funkcija 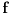 na nekom intervalu  definisana onda se za nju kaže da je Jensen konveksna (ili J-konveksna) ako zadovoljava uslov 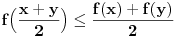 na tom intervalu. Taj uslov je slabiji od uslova konveksnosti koji glasi 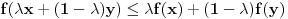 za sve 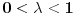 i sve 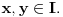 Funkcije koje su J-kionveksne, ali nisu konveksne, ne mogu se konstruisati (odnosno ne može se zapisati kako izgledaju), ali se može dokazati da postoje. Drugim rečima, iz uslova J-konveksnosti se ne može izvesti uslov konveksnosti. Ukoliko pretpostaviš samo J-konveksnost funkcije 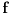 na intervalu 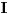 koji se sastoji od više od jedne tačke, za 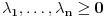 za koje je 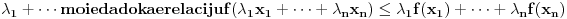 za sve 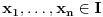 tačno u slučaju kada su  racionalni brojevi.
Da bi funkcija 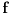 bila konkveksna na intervalu 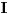 potrebno je i dovoljno da na njemu bude J-konveksna i da bude neprekidna u njegovoj unutrašnjosti. Takođe, sa konveksnošću funkcije 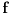 na intervalu 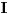 ekvivalentno je da je ta funkcija J-konveksna na njemu i da za svako 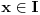 postoji okolina 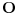 tačke 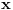 takva da je funkcija 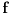 ograničena na skupu 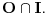 [ Nedeljko @ 14.06.2005. 11:05 ] @
Takođe, koveksna funkcija ne mora biti nijedanput (a kamoli dvaput) diferencijabilna. Međutim, ako je funkcija na nekom intervalu dva puta diferencijabilna, onda je ona na njemu konveksna ako i samo ako joj je drugi izvod nenegativan.
[ uranium @ 16.06.2005. 22:56 ] @
Citat: Nedeljko: Funkcije koje su J-konveksne, ali nisu konveksne, ne mogu se konstruisati (odnosno ne može se zapisati kako izgledaju), ali se može dokazati da postoje.Drugim rečima, iz uslova J-konveksnosti se ne može izvesti uslov konveksnosti.
Ovo je vrlo zanimljivo 
Ako sam dobro shvatio, kad bi uslov konveksnosti bio izvodljiv iz uslova J-konveksnosti, onda bi te (postojeće a neiskazive) f-je bile zapisive?
Kada kažeš izvodljiv, da li misliš na konstrukciju formalnog dokaza?
Nedeljko, da li bi mogao, ako te ne mrzi, da elaboriraš ovo malo?
[ Nedeljko @ 17.06.2005. 00:09 ] @
Formalno se dokazuje da postoje J-konveksne funkcije koje nisu konveksne. Međutim, tu se koristi Cornova lema i samo se dokazuje da takva funkcija postoji. Sama funkcija se ne konstruiše.
Recimo, polje R možeš posmatrati kao vektorski prostor nad poljem Q kao poljem skalara. Dimenzija vektorskog prostora R nad poljem skalara Q je beskonačna (čak kontinuum). Pomoću Cornove leme dokazuje se da svaki vektorski prostor (nad bilo kojim poljem skalara) ima bazu. Neka su A i B dve baze vekstorskog prostora R nad poljem skalara Q takve da 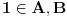 . Takođe pomoću Cornove leme dokazuje se da su svake dve baze istog vektorskog prostora ekvipotentne (postoji bijekcija između njih). Sve ovo je dokazano na primer u algebri od Veselina Perića. Svako preslikavanje baze vektorskog prostora u neki (moguće i drugi) vektorski prostor nad istim poljem skalara se može na tačno jedan način dopuniti do linearnog preslikavanja između tih vektorskih prostora. To preslikavanje je 1-1 ako i samo ako je slika baze (kao familije vektora) linearno nezavisna familija vektora, odnosno to preslikavanje je na ako i samo ako je slika baze generatrisa prostora kodomena.
Presliakaj bijektivno bazu A na bazu B uz jedine uslove da se jedinica slika u sebe i da se to preslikavanje ne svede na identitet (ako su baze A i B iste). To preslikavanje ćeš moći da dopuniš do linearne (u odnosu na polje skalara Q) bijekcije f vektorskog prostora R na sebe samog koje se na Q svodi na identitet. Ne samo da će f biti J-konveksno, nego će umesto nejednakosti važiti jednakost. Međutim, ako bi bilo konveksno, bilo bi i neprekidno, pa bi zbog svođenja na identitet na Q bilo identitet i na R, što je u suprotnosti sa našim izborom presliakvanja koje bar jedan bazni vektor ne slika u sebe. Ako ti se ne sviđa što funkcija nije strogo J-konveksna, možeš da je sabereš sa 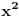 . [ uranium @ 17.06.2005. 02:38 ] @
Sjajno si to objasnio! 
Mnogo ti hvala!!
[ Metalnem @ 23.06.2005. 20:52 ] @
Evo necega sto se ne moze nazvati nejednakoscu, ali je cesto veoma korisno pri dokazivanju nejednakosti:
Lagranzov metod multiplikatora
Neka su na otovorenom skupu 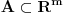 definisane neprekidno diferencijabilne funkcije 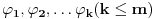 i 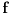 . Ako funkcija 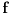 pri uslovima 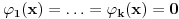 ima lokalni ekstremum u tacki 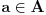 , tada postoje realni brojevi  , takvi da funkcija 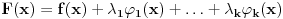 u tacki 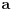 ima izvod 0 po svakoj od 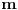 koordinata.
Teorema opisuje neophodne uslove ekstremuma koji ne moraju biti i dovoljni, ali u zadacima nije ni potrebno vise od toga.
Primer:
Dat je trougao 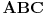 sa duzinama stranica 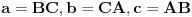 . Odrediti tacku 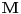 unutar tog trougla tako da je vrednost izraza 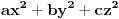 minimalna, ako su 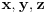 rastojanja tacke 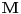 redom pravih 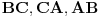 .
Posto je 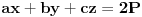 , ovde mozemo formirati Lagranzovu funkciju
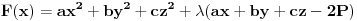 sa jednim multiplikatorom 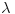 . Izjednacavanje njenih parcijalnih izvoda sa nulom daje uslove
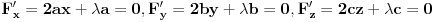 , sto zajedno sa uslovom 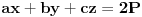 daje sistem od cetiri jednacine iz kojih se odredjuje 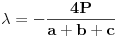 i 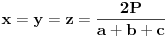 . Posto je 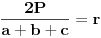 (gde je 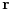 centar upisanog kruga), jasno nam je da je trazena tacka centar upisanog kruga u dati trougao. [ Nedeljko @ 24.06.2005. 20:07 ] @
Ispustio si jedan uslov iz te teoreme, a to je da matrica
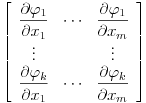
ima rang jednak 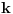 u tački 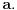 [ Metalnem @ 24.06.2005. 20:11 ] @
Interesantno, posebno zato sto to ne pise u knjizi iz koje sam izvukao ovu teoremu.
[ Nedeljko @ 24.06.2005. 22:18 ] @
Pogledaj neku knjigu u kojoj je teorema dokazana, pa vidi šta se koristi u dokazu.
[ Nedeljko @ 27.12.2005. 09:39 ] @
Pošto ne mogu da menjam poruke starije od 60 dana, a uočio sam grešku prilikom kucanja jedne od svojih prethodnih poruka, ispravljam je na ovaj način.
Jedna mala ispravka:
Citat: cassey: [Funkcija 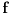 je konveksna na intervalu 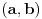 ako za svako par brojeva 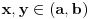 vazi 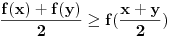 , sto je ekvivalentno sa uslovom 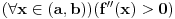 .
Ako je funkcija 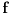 na nekom intervalu 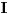 definisana onda se za nju kaže da je Jensen konveksna (ili J-konveksna) ako zadovoljava uslov 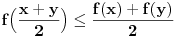 na tom intervalu. Taj uslov je slabiji od uslova konveksnosti koji glasi 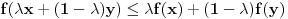 za sve 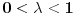 i sve 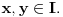 Funkcije koje su J-kionveksne, ali nisu konveksne, ne mogu se konstruisati (odnosno ne može se zapisati kako izgledaju), ali se može dokazati da postoje. Drugim rečima, iz uslova J-konveksnosti se ne može izvesti uslov konveksnosti. Ukoliko pretpostaviš samo J-konveksnost funkcije 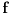 na intervalu 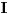 koji se sastoji od više od jedne tačke, za 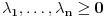 za koje je 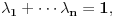 moći ćeš da dokažeš relaciju 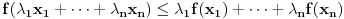 za sve 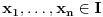 tačno u slučaju kada su  racionalni brojevi.
Da bi funkcija 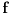 bila konkveksna na intervalu 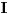 potrebno je i dovoljno da na njemu bude J-konveksna i da bude neprekidna u njegovoj unutrašnjosti. Takođe, sa konveksnošću funkcije 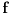 na intervalu 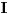 ekvivalentno je da je ta funkcija J-konveksna na njemu i da za svako 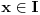 postoji okolina 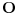 tačke 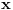 takva da je funkcija 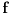 ograničena na skupu 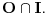 [ Sonec @ 05.02.2012. 00:14 ] @
Mislio sam da ne bi bilo lose da se i pokazu ove nejednakosti  pa sam ja.... Elem, na osnovu konkavnosti logaritamske funkcije imamo
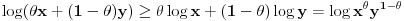 za 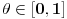
Kako je 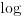 za osnovu 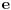 rastuca funkcija, to onda vazi 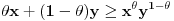
Oznacicemo 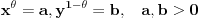 , tj. 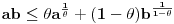 . Oznacimo 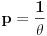 i 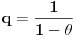 i tada vazi 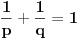 gde su 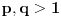 (iz cinjenice da 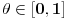 )
Tada dobijamo 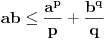 - Jangova nejednakost (Young). Jednakost vazi akko 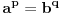 Helderova nejednakost (Hölder)
Helderova nejednakost (Hölder): 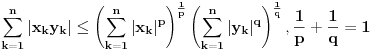 (za 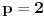 (tada je i 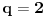 ) dobija se Kosi-Svarzova nejednakost (Cauchy–Schwarz)).
Pokazacemo je za 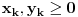 , za negativne se primeni 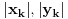 .
Obelezimo 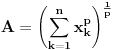 i 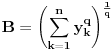
Primenimo Jangovu nejednakost na 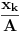 i 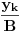
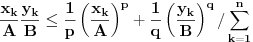 (primenjujemo Jangovu nejednakost 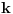 puta)
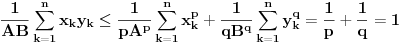
Dobijamo 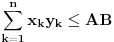 , odnosno 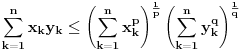 Q.E.D.
Dokazujemo nejednakost Minkovskog (Minkowsky) za 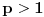 (za 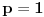 se svodi na nejednakost trougla)
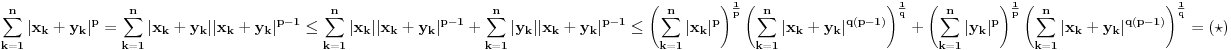 (kod poslednjeg znaka nejednakosti smo iskoristili Helderovu nejednakost na oba sabirka).
Kako je 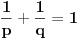 , odnosno 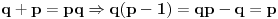
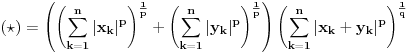
Dobili smo 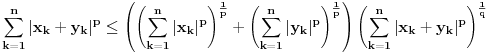 , odnosno 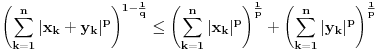 , al kako je 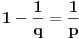 to na kraju dobijamo 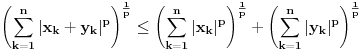 sto je i trebalo pokazati Q.E.D.
Bila jedna sitna greskica, al niko nije primetio  [Ovu poruku je menjao Sonec dana 05.02.2012. u 18:17 GMT+1]
[Ovu poruku je menjao Sonec dana 05.02.2012. u 18:17 GMT+1][ ortodox888 @ 18.09.2013. 20:34 ] @
Kad već ovako sve lepo dokazujete dokažite i ovu ekvivalenciju kad važi jednakost u Helderovoj nejednakosti.
[ Sonec @ 18.09.2013. 21:39 ] @
Pozdrav za mog kolegu i drugara :-)
Pa sad, ne znam koja ti je to OVA ekvivalencija kad vazi jednakost kod Holdera (i to kod kog Holdera, da li mislis na onog u L^p prostorima ili se zadoljavas sa ovim iznad).
Ali, s obzirom da u dokazu Holdera koristis Jangovu nejednakost, a da tamo jednakost vazi ako i samo ako je 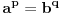 , to onda ne bi trebalo da ti bude problem da pokazes kad vazi jednakost kod Holdera.
Uostalom, sutra pravac biblioteka, uzmi Jocicevu knjigu i naci ces sve.
A postoji naravno i google.
Uostalom, ja sam mislio da ti napisem dokaz, al trenutno forum ima problem sa LaTeX-om, pa nisam u mogucnosti.
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|