Samo momenat, nije mi jasno ako ti već imaš dokaz za (2) zašto onda tražiš drugačiji? Na svakom ispitu, takmičenju, šta god, ako je zadatak tačno rešen moraju ti priznati rešenje bez obzira na to da li se ono razlikuje od predviđenog. Jedino ako možda želiš da znaš zbog tebe lično, to je onda druga stvar.

_{[Ovu poruku je menjao Bojan Basic dana 26.08.2006. u 23:27 GMT+1]}

Da, baš tako
U postavci je pisalo :"...koristeći (1), dokazati...".

Prvo primetimo da je

Iz definicije Mebijusove funkcije sledi da ovde otpadaju svi članovi kod kojih je deljivo kvadratom nekog prostog broja. Dalje, neka nije deljivo nekim prostim faktorom broja i neka nije deljivo niti jednim kvadratom prostog broja. Tada se brojevi za koje pojavljuju u parovima oblika a pošto za njih važi iz prethodne jednačine dobijamo da važi

gde su svi međusobno različiti prosti faktori broja

Dalje, primetimo da je jednačinom od koje smo pošli funkcija jedinstveno određena. Zaista, , pa je vrednost funkcije jednoznačno određena u tački a vrednost u bilo kojoj drugoj tački joj je određena vrednostima u manjim tačkama jednačinom

gde se sumiranje vrši po svim deliteljima broja koji su manji od Iz toga i iz činjenice da funkcija

ispunjava uslov sledi da je

No, odatle se dobija da je

što je i trebalo dokazati.

_{[Ovu poruku je menjao Nedeljko dana 16.06.2005. u 17:23 GMT+1]}

Nedeljko hvala ti na ovom rešenju. Vrlo lukavo!

Ne zameri, ali moram da primetim da je upotreba jednakosti (1) i u tvom rešenju ipak sasvim suvišna (iako ingeniozna).
Naime, kada si već stigao do:



može se direktno proveriti da je to jednako sa
za i je
a za k=1 je

Ja sam do te jednakosti i stigao primenom jednakosti (1). Međutim, bilo mi je glupo da koristim eksplicitan oblik funkcije bez dokaza, pa sam i nju dokazao opet preko jednakosti (1), čisto da bi sve bilo dokazano preko nje.

Da, da...izvini zbog ovog previda...

Hvala još jednom!

Skoro smo na vezbama radili ovaj zadatak , isto preko Mangoldt-ove funkcije, al na drugi nacin, pa nije lose i da se i on napise.
Pre dokaza, neke uvodne napomene:

za sve
Def. Ako su i dve aritmeticke funkcije onda definisemo aritmeticku konvuluciju funkcija i .

Neke osobine:
1) je komutativna i asocijativna operacija na skupu aritmetickig funkcija
2) je neutral za , tj. za sve

Najosnovnija formula:
Möbius-ova inverzija: aritmeticke funkcije, tada
Dokaz zadatka iz uvodnog posta:
Prema Osnovnoj teoremi aritmetike
(ovde je trik, kada pomnozimo sa 1), odnosno
Möbius-ovom inverzijom dobjamo , odnosno ( je komutativna operacija)
jer je

Nama je asistent otisao jos dalje u prici o Mangoldt-ovoj funkciji, stigao je i do Riman zeta funkcije i dokazao da je (rekao nam je da cemo to raditi detaljnije iz kompeksne analize, al voli on tako da odluta i da nam pokaze lepotu matematike).

_{[Ovu poruku je menjao Sonec dana 15.01.2012. u 14:47 GMT+1]}

Malo mi je "supalj" prethodni post, pa cu ga dopuniti sa nekim dokazima.



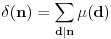
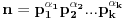
. Na osnovu Osnovne teoreme aritmetike , a kako je i multiplikativna aritmeticka funkcija to vazi
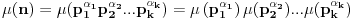
Na osnovu definicije Möbius-ove funkcije imamo

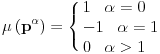
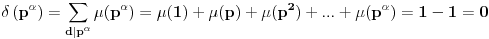
Pa je tada (za )
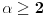
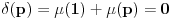
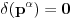
. Dakle, za , .
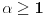
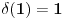
I onda dobijamo

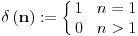
Dobro, sada znamo zbog cega je definisana na taj nacin, al otkud znamo da je ona multiplikativna aritmeticka funkcija? Odgovor na to pitanje nam daje sledeca teorema:
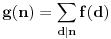
Teorema. Neka je multiplikativna aritmeticka funkcija. Tada je takodje multiplikativna aritmeticka funkcija.

Pre dokaza definicaja multiplikativne aritmeticke funkcije:
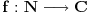
Definicija. Neka . Za funkciju kazemo da je multiplikativna aritmeticka funkcija akko ().

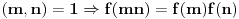
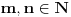
Pre dokaza teoreme navodim i jednu lemu koju necu dokazivati:
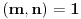
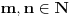
Lema. Neka su ( i uzajamno prosti brojevi), . Tada .

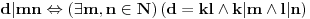
A sada sam dokaz teoreme:
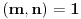
Dokaz. Dokazujemo da je multiplikativna aritmeticka funkcija. Pretpostavimo , tada je

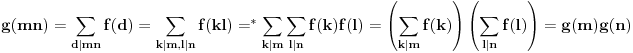
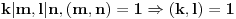
* QED.


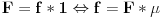
Pokazacu smer () koji sam ja koristio u dokazu (prethodan post). Dakle, dokazujemo:
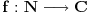
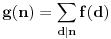
Teorema (teorema inverzije). Neka je multiplikativna aritmeticka funkcija, i neka je . Tada je .

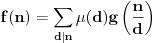
Pre dokaza, primetimo da vazi: .

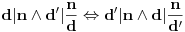
A sada i dokaz teoreme inverzije:
Dokaz. 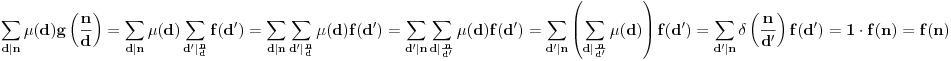QED.

Eto, valjda sam sad bar malo razjasnio svoj prethodni post.