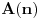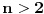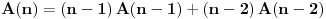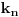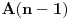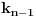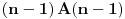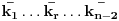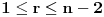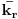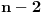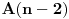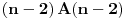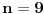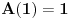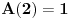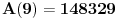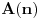
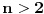
Ako sa označimo broj ispravnih rasporeda pri vraćanju kamila , onda, za , važi:

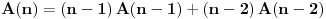
Dokaz:
Ispravne kolone dužine se mogu dobiti na dva različita načina:
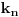
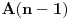
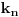
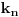
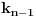
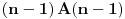
1. Izdvojimo kamilu . Ostatak kamila može da se rasporedi ispravno na načina u novu kolonu, a za svaki od njih mi možemo kamilu smestiti na tačno od postojećih mesta unutar te kolone (kamila ne sme da se stavi jedino iza kamile ). Na ovaj način možemo napraviti različitih ispravnih kolona.

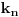
2. Izdvojimo kamilu . Ostatak kamila može da se rasporedi u kolonu u kojoj je tačno jedan par kamila u pogrešnom poretku.
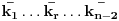
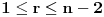
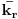
Posmatrajmo sada te dve pogrešno poređane kamile kao jednu novu kamilu. U tom smislu možemo da preoznačimo postojeću kolonu kamila na sledeći način: gde je a "kamila" koju smo dobili spajanjem.
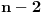
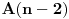
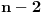
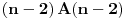
Ova kolona od kamile može se ispravno poređati na načina, a pošto se dve pogrešno poređane kamile mogu odabrati na načina, to je ukupan broj kolona sa tačno jednim parom kamila u pogrešnom poretku jednak. Sada se u svaku od tako dobijenih kolona može umetnuti kamila 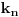između one dve pogrešno postavljene kamile i time dobiti potpuno ispravna kolona.

Očigledno je da među kolonama dobijenim na način 1. i način 2. nema jednakih.

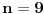
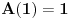
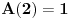
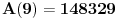
U postavci zadatka je , pa ako po definiciji uzmemo da je , a lako je videti da je , onda možemo da izračunamo i (izračunavši prethodno ).

Zadatak je u principu mogao da se reši i preko principa "uključenja-isključenja" ali bi u tom slučaju bilo daleko više posla.

Nadam se da će neko rešiti dobijenu diferencnu j-nu.

mozda je ipak lakse principom ukljucenja-iskljucenja?