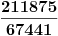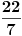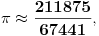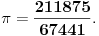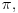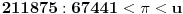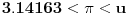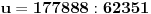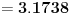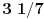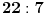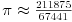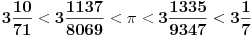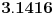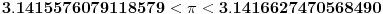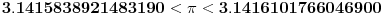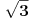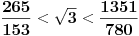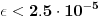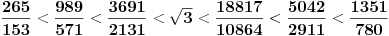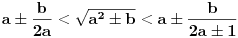Istina je. Arhimed je dokazao nejednakost koju pominješ, ali dotična aproksimacija je takođe njegova.

OK.
Pitanje glasi
U KOM DELU JE ON TO NAVEO?

Za sada je odgovor:
NI U JEDNOM!

Meni ovo malo mirise da je neko malo podmetnuo Wikipediji.

Pozdrav ljubiteljima antike...

D. Blatner, The Joy of Pi, Walker & Company, 1999:

"Istoričari matematike još uvek se spore oko toga da li je Apolonije (Arhimedesov kolega, mlađi trideset godina od njega) ili Arhimedes poboljšao granicu na ."

(slobodan prevod)

Eto, toliko sam ja našao o tome kad već tražiš zvanične reference, a u kom je to delu objavljeno verovatno nikad nećemo saznati (što opet ne znači da nikad nije objavljeno).

Interesuje me što si ti do te mere opčinjen vrednošću da čak ovu aproksimaciju nazivaš klevetom (???) kada je daleko bolja od citirane?

Ako se dobro secam, Arhimed je vec imao osecaj za infinitezimalni racun, pa je razmisljao da bi se povrsina ispod krive linije mogla izracunati ucrtavanjem sve manjih i manjih pravougaonika, pa me ne bi cudilo da je dosao i do ove aproksimacije.

U nekoj americkoj drzavi su zakonom proglasili da je Pi = 3. Srecom, to je kratko trajalo :)

Čekaj, ako je reč o aproksimaciji, onda je zapravo
a ne Ovo drugo nikako nije tačno jer je broj iracionalan. Da je Arhimed tvrdio da je to jednako, svakako bi negde imao grešku u zaključivanju. On je koliko znam tvrdio za te racionalne aproksimacije da su blizu a to je već nešto drugo. Inače, imao je delo sa naslovom "merenje kruga".

_{[Ovu poruku je menjao Nedeljko dana 27.06.2005. u 23:53 GMT+1]}

> D. Blatner, The Joy of Pi, Walker & Company, 1999:
> "Istoričari matematike još uvek se spore oko toga da li je Apolonije ......

To je ono pravo! Ovo ima smisla.

Poznato je da je Apolonijus lagano pljuckao po Arhimedu (a posle njega jos neki)
jer je i Arhimed umeo da podmece (pogotovo Aleksandrijskoj skoli, odakle su mu ortaci krali radove i objavljivali kao svoje na sta im se ovaj svetio tako sto im je slao dokaze
LAZNJAKE sto su ovi potom takodje objavljivali kao svoje).

Samo onda treba reci
POSTOJE INDICIJE DA JE APOLONIJUS DAO APROKSIMACIJU X/Y
(znaci nije ni Arhimed ni Vitruvius)


Povodom primedbe o tome da nije Pi=211875/67441, izvinjavam se jer sam kucao u ASCII
a tu nema "priblizno".

ZAKLJUCAK: Cak i u Wikipediji se desavaju podvale a ekipa ne otklanja. Sva sreca da nema srpski prevod.

Usput, jel ima neko neku dobru knjigu o Pi?

Što se tiče Vitruviusa ne znam odakle sad njega izvuče pošto je on živeo oko 200 godina posle Arhimeda. A da li je Arhimed ili Apolonije "odgovoran" za spornu aproksimaciju, to se, kako smo ustanovili, još uvek ne zna, i nije mi jasno zašto insistiraš da je u pitanju podvala - kogod da je to napisao sigurno nije imao nameru da nešto podvaljuje već je verovao da je u pitanju Arhimed (kao što sam i ja mislio pre nego što sam našao gorecitirani izvor, a tako mislim još uvek jer je Apolonije imao dosta manje radova na tu temu od Arhimeda).

Evo još jedne zanimljivosti:

P. Beckmann, A History of Pi, St. Martin's Griffin, 1976:



Za sada vodi Arhimed sa 2:1.

_{[Ovu poruku je menjao Bojan Basic dana 28.06.2005. u 18:04 GMT+1]}

Ej, hvala za Herona. Prava stvar!

Inace


Zbog lošeg formatiranja tabela na web strani dati razlomak se nalazi između Arhimeda i Vitruviusa što prilično zbunjuje.
Možeš pogledati
http://encyclopedia.worldvillage.com/s/b/Pi



Za sada istraga napreduje ovako:
Arhimed je u Teoremi 3 dao kako izgleda iteracioni postupak i obrnuo ga četiri puta.
Došao je do rezultata


Apolonius je možda napisao nešto o tome (dakle ne znamo ni za jedan rad, samo možda) a o tome znamo samo jer je Eutocius spomenuo da je Apolonius izračunao bolju aproksimaciju.
http://www-groups.dcs.st-and.a...Mathematicians/Apollonius.html


Ok, stvar je u tome što ja veoma cenim ideju Wikipedije i smatram da su sve reference obrađene od ljudi koji o tome znaju najbolje. Zato mi nije svejedno ako pomislim da je nešto netačno. Drugo, izuzetno mi je krivo što ne postoji veći broj referenci sa tekstom na srpskom jeziku. Kada bi samo nas nekoliko dnevno po jednu referencu prevodili srpski jezik bi se našao u društvu svetskih jezika i na Wikipediji.

A ono za Herona, nasao sam da negde postoji nemački prevod Metrike a za engleski nije sigurno.

Na linku koji si ostavio nisam video o kojoj aproksimaciji Eutocius govori, samo toliko da je bolja od . Ja sam pronašao da je ta Apolonijeva aproksimacija zapravo .

Izvori:
1) G. Donald Allen, The Hellenistic Period, 2000;
2) http://www.mlahanas.de/Greeks/Conics.htm

_{[Ovu poruku je menjao Bojan Basic dana 04.07.2005. u 13:54 GMT+1]}

Ni ja nisam našao aproksimaciju. Sumnjam da i postoji. I na ovom sajtu se spominje samo da je postojala knjiga "Brz račun" u kojoj je data aproksimacija 3.1416. Usput Grci sigurno nisu pisali sa decimalnom tačkom pa verujem da je aproksimacija originalno data u obliku razlomka.

Svodi se na sledeće: Apolonije je bio profa u Aleksandrijskom Muzeonu. Kao i sve današnje profe maltretirao je svoje đake i mlađe kolege raznim zadacima koi su njemu bili mrski ili ispod časti.

Veoma je verovatno da je neki učenik uradio Arhimedov postupak samo još neki korak dalje. Analitički tačan račun Arhimedovog postupka daje sledeće
za 384-ougao
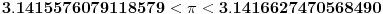
za 768-ougao
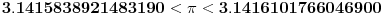
već kod 1536-tougla se pojavljuju sigurne decimale 3.14159 što je preciznije od Apolonijusovog približenja.

Međutim tu se postavlja pitanje prve aproksimacije za .
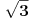
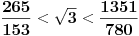
Ako se koristi Arhimedova (poznata od Vavilonaca) aproksimacija ona daje opseg apsolutne greške .
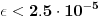
Koristeći De Lanjijev tj Tanerov metod možemo nastaviti lanac aproksimacija
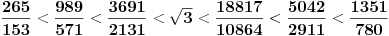
i ako bi se za sve korene koristila (Grcima poznata) formula

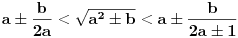
moglo bi se nastaviti u nekoliko pravaca traženje ali ova forenzičarska metoda ima samo jednu i ultimativnu manu - nemamo telo tojest ciljni razlomak čije izvođenje dokazujemo.

Zaključak (po meni): Arhimed je tata. Postavio je domaći zadatak i svi su 18 vekova prepisivali. Nije genijalna samo njegova metoda već i jednostavne krajnje aproksimacije.