Pre svega, jednačina ima rešenja:
npr:

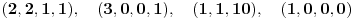
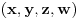
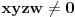
Ako je rešenje i ako je , onda je .
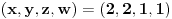
Dokaz:

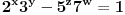
Neka je , onda sledi:
.
Posmatrajmo sada čemu su jednaki stepeni dvojke, odnosno trojke po modulu 35.

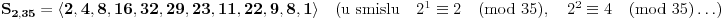
i slično .

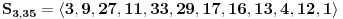
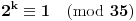
Primetimo da su redovi i broja 2 i broja 3 po modulu 35 jednaki 12, tj. prvi pozitivan broj za koji važi je 12 i isto za broj 3.
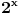
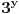
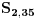
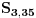
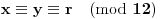
E sad da bi važilo brojevi i moraju biti uzajamno inverzni po modulu 35, a odatle je lako videti, na osnovu f-ja i , da su jedine mogućnosti gde je
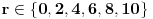
(Mogli su se sa manje računa razmatrati odvojeno ostaci pri deljenju sa 5 i odvojeno ostaci pri deljenju sa 7)
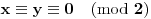
U svakom slučaju dobili smo da je . Dakle, i su makar 2, ali ne više od toga jer:
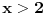
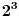
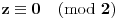
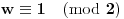
ako pogledamo čitavu polaznu jednačinu po modulu 3 vidimo da mora biti neparno, pa ako bi, recimo bilo , onda bi dobili (posmatrajući celu jednačinu po modulu ) da je a ispitivanjem stepenova broja 5 i broja 7 po modulu 8, dobija se da mora biti i , što je očigledno nemoguće, jer je neparno. Dakle, .
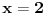
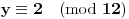
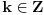
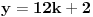
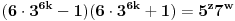
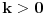
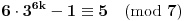
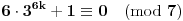
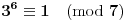
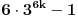
Pošto su i kongruentni po modulu 12, sledi , tj. postoji za koje važi , tako da polazna jednačina postaje . Pretpostavimo da je . Sada, analizom faktora na levoj strani po modulu 7, dobijamo da je i , jer je . Analizom istih faktora po modulu 5, dobijamo da je, u zavisnosti od parnosti broja , tačno jedan od njih deljiv sa 5. 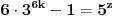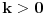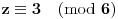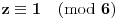Odatle lako sledi da mora biti parno (jer u protivnom broj ne bi bio deljiv ni sa 5 ni sa 7).Dakle, možemo zaključiti da važi , onda, analizom po modulu 9 (jer je po pretpostavci ), sledi da je (red broja 5 po modulu 9 je 6), a analizom iste jednačine po modulu 7, dobijamo da mora biti (red broja 5 po modulu 7 je 6). 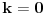Dakle, dobili smo kontradikciju, pa je a time i .
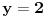
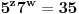
Polazna jednačina sada postaje a odatle sledi tvrđenje.

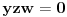
Razmotrimo sada slučaj, kada je , (jer jasno je da )

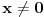
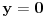
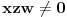
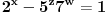
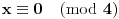
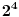
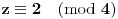
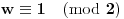
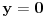
Neka je i , onda analizom jednačine po modulu 5 (kao i u ranijim slučajevima), dobijamo da važi , pa zatim analizom iste jednačine ali po modulu dobijamo da mora biti i (dakle, redovi brojeva 5 i 7 po modulu 16 su 4 i 2), a to ne može biti, jer mora biti neparno. Dakle, ne može biti i .

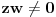
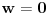
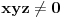
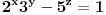
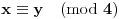
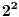
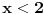
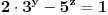
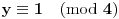
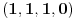
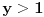
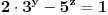
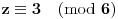
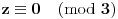
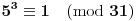
Neka je i , onda analizom jednačine po modulu 5 (kao i u ranijim slučajevima), dobijamo da važi , pa zatim analizom iste jednačine ali po modulu dobijamo da je , pa na osnovu pretpostavki , sada je jasno (analizom jednačine po modulu 5), da mora biti , odatle, nalazimo rešenje . Ako bi bilo onda bi analizom j-ne po modulu 5, na uobičajen način dobili prvo , a odatle i . 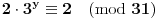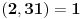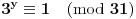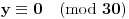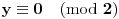Sada,budući da je , dobijamo j-nu , odatle, kako je , dobijamo da je , odatle sledi , (jer je red broja 3 po modulu 31 jednak 30), pa dobijamo da je što je u suprotnosti sa . 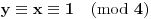Kontradikcija.
Dakle, jedino rešenje je .

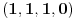
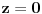
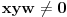
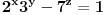
Neka je i , onda analizom jednačine po modulu 6 dobijamo da ona nema rešenja.

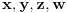
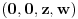
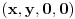
Ako su neka 2 od jednaka 0. Slučaj je nemoguć kao i slučaj , pa ostaje da razmotrimo .

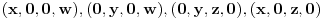
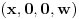
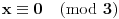
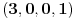
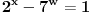
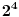
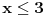
U slučaju dobijamo da je , pa dobijamo jedinstveno rešenje , jer se proverom jednačine po modulu dobija da j-na nema rešenja, pa sledi , tj..

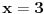
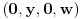
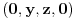
U slučajevima i , nema rešenja, jer je razlika 2 neparna broja, paran broj.

I preostali slučaj je nemoguć, što je lako videti analizom j-ne po modulu 3.

U slučaju da je samo jedan od eksponenata različit od 0, onda lako dobijamo da je jedino rešenje: .

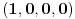
Time su (nadam se) pronađena sva rešenja.
Valjda će se neko potruditi da ovo malo uprosti (meni je muka od ovog zadatka)




<sub>[Ovu poruku je menjao uranium dana 04.07.2005. u 00:58 GMT+1]

[Ovu poruku je menjao uranium dana 04.07.2005. u 01:00 GMT+1]</sub>

Sad sam primetio jednu rupu, gledaću da to brzo otklonim

Svala čast! Ta rupa koju pominješ nije uopšte velika i može se vrlo lako otkloniti (pretpostavljam da mislimo na isto, pošto sam samo ovo našao).

Jednačina zapravo glasi iz čega zaključujemo pa opet dolazimo do .

Moje rešenje (nešto drugačije od ovog, ali esencijalno je isto) ću postaviti za par dana pošto trenutno nisam kod kuće a tamo imam već iskucano u pdfu.

Evo uneo sam neophodne izmene.

Bojane, hvala ti na otkrivanju one greške (nisam je primetio )

Kao što sam i obećao, evo mog rešenja pa ko hoće može da pročita i prokomentariše.