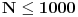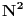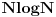|
|
[ stf @ 04.07.2005. 11:25 ] @
|
| Sledeći zadatak je sa USACO-a. Rešavanje istog ne polazi mi za rukom, jer niz sa 10000*10000 članova prevazilazi memorijsko ograničenje. Možete li da mi ponudite neki algoritam, koji zauzima manje memorijskog prostora, jer ne znam kako ovo rešim, a da ne formiram niz čiji elementi prestavljaju svako polje. Zadatak glasi:
Shaping Regions
N opaque rectangles (1 <= N <= 1000) of various colors are placed on a white sheet of paper whose size is A wide by B long. The rectangles are put with their sides parallel to the sheet's borders. All rectangles fall within the borders of the sheet so that different figures of different colors will be seen.
The coordinate system has its origin (0,0) at the sheet's lower left corner with axes parallel to the sheet's borders.
PROGRAM NAME: rect1
INPUT FORMAT
The order of the input lines dictates the order of laying down the rectangles. The first input line is a rectangle "on the bottom".
Line 1: A, B, and N, space separated (1 <= A,B <= 10,000)
Lines 2-N+1: Five integers: llx, lly, urx, ury, color: the lower left coordinates and upper right coordinates of the rectangle whose color is `color' (1 <= color <= 2500) to be placed on the white sheet. The color 1 is the same color of white as the sheet upon which the rectangles are placed.
SAMPLE INPUT (file rect1.in)
20 20 3
2 2 18 18 2
0 8 19 19 3
8 0 10 19 4
INPUT EXPLANATION
Note that the rectangle delineated by 0,0 and 2,2 is two units wide and two high. Here's a schematic diagram of the input:
11111111111111111111
33333333443333333331
33333333443333333331
33333333443333333331
33333333443333333331
33333333443333333331
33333333443333333331
33333333443333333331
33333333443333333331
33333333443333333331
33333333443333333331
33333333443333333331
11222222442222222211
11222222442222222211
11222222442222222211
11222222442222222211
11222222442222222211
11222222442222222211
11111111441111111111
11111111441111111111
The '4's at 8,0 to 10,19 are only two wide, not three (i.e., the grid contains a 4 and 8,0 and a 4 and 8,1 but NOT a 4 and 8,2 since this diagram can't capture what would be shown on graph paper).
OUTPUT FORMAT
The output file should contain a list of all the colors that can be seen along with the total area of each color that can be seen (even if the regions of color are disjoint), ordered by increasing color. Do not display colors with no area.
SAMPLE OUTPUT (file rect1.out)
1 91
2 84
3 187
4 38
|
[ sklitzz @ 04.07.2005. 12:23 ] @
Potrazi malo po forumu ovaj zadatak se vec spominjao(shaping regions)
[ cassey @ 04.07.2005. 13:14 ] @
Da, ovaj zadatak je stvarno tezak, doduse ovde je 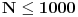 pa se moze raditi i u 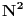 medjutim npr. na Saratovu je ogranicenje mnogo, nogo vece pa zahteva slozenost 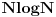 ...
Ja resenje u 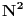 imas Hint na USACO-u tipa:
Code:
+--------+ +-+--+--+
| | | |2 | |
| | + +--+ |
| +-+ | --> | | | |
| +-+ | |1| |3 |
| | | +--+ |
| | | | 4| |
+--------+ +-+--+--+
Podelis na te delove i ides redom po soritranim x-koordinatama (podelis ga na trake pa svaku traku zasebno posmatras...)
[ stf @ 04.07.2005. 13:14 ] @
Tražio sam na pretraživaču ('shaping regions'), a i po ovom podforumu i nisam ništa našao. Znaš li neku ključnu reč iz te teme koja je slična ovoj?
[ stf @ 04.07.2005. 13:17 ] @
Cassey, valjalo bi da vidim to rešenje za O(n log n), jer ovo sa n^2 ne prolazi.
[ cassey @ 04.07.2005. 15:25 ] @
Ma mora da ti prodje i 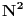 . Znaci algoritam je sledeci:
Podelices onaj polazni kvadrat na trake (kao na onoj slici u mom prethodnom postu)... To uradis tako sto sortiras sve (i polazne i krajnje) tacke tih kvadrata koje bojis. I sada ces svaku traku posebno posmatrati na sledeci nacin: opet svaku traku podesli (ali sada prema y osi) na manje "trakice" i svaka od tih trakica je obojena jednom bojom i ti samo povrsinu te boje povecas za rasliku tih y-ilona * x-ilona (sirine trake)... E sto se tice ove druge slozenosti, algoritam se zasniva na istome stim sto ces ovde u Heap-u, cuvati ove trakice koje si soritao po y-onu, soritane po tome koja je zadnja obojena pa ona koja je zadnja obojena tu povrsinu treba da povecas... Svaki kvadrat ce najvise 3 puta da udje u neku traku i tacno toliko puta da izanje iz Heap pa je slozenost 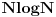 ...
[ cassey @ 04.07.2005. 15:27 ] @
Evo ti moj kod ako ti nesto znaci...
Srecno... :-)
Code:
program rect1;
{$APPTYPE CONSOLE}
uses
SysUtils;
const
MaxN = 2505;
var
pom, dx, dy, Area, Heap, Pos, x, y, color: array [1.. MaxN] of LongInt;
n, d, Size: LongInt;
f, g: Text;
procedure InPut;
var
i, a, b: LongInt;
begin
Assign (f, 'rect1.in');
Reset (f);
Read (f, a, b, n);
Inc (n);
x [1] := 0; y [1] := 0;
x [n + 1] := a; y [n + 1] := b;
Color [1] := 1;
for i := 2 to n do
Read (f, x [i], y [i], x [n + i], y [n + i], Color [i]);
Close (f);
end;
procedure Quick_Sort_X (l, r: LongInt);
var
i, j, tmp, pivot: LongInt;
begin
if (l < r) then begin
pivot := pom [(l + r) DIV 2];
i := l; j := r;
repeat
while (pom [i] < pivot) do Inc (i);
while (pom [j] > pivot) do Dec (j);
if (i <= j) then begin
tmp := pom [i]; pom [i] := pom [j]; pom [j] := tmp;
Inc (i); Dec (j);
end;
until (i > j);
Quick_Sort_X (l, j);
Quick_Sort_X (i, r);
end;
end;
procedure Quick_Sort_Y (l, r: LongInt);
var
i, j, tmp, pivot: LongInt;
begin
if (l < r) then begin
pivot := pom [(l + r) DIV 2];
i := l; j := r;
repeat
while (pom [i] < pivot) do Inc (i);
while (pom [j] > pivot) do Dec (j);
if (i <= j) then begin
tmp := pom [i]; pom [i] := pom [j]; pom [j] := tmp;
tmp := dy [i]; dy [i] := dy [j]; dy [j] := tmp;
Inc (i); Dec (j);
end;
until (i > j);
Quick_Sort_Y (l, j);
Quick_Sort_Y (i, r);
end;
end;
procedure Exc (var a, b: LongInt);
var
tmp: LongInt;
begin
tmp := a; a := b; b := tmp;
end;
procedure Insert (v: LongInt);
var
p, q: LongInt;
begin
Inc (Size);
Heap [Size] := v;
Pos [v] := Size;
p := Size;
q := p DIV 2;
while (q > 0) and (Heap [q] < Heap [p]) do begin
Exc (Pos [Heap [p]], Pos [Heap [q]]);
Exc (Heap [p], Heap [q]);
p := q;
q := p DIV 2;
end;
end;
procedure Delete (x: LongInt);
var
p, q: LongInt;
begin
Heap [Pos [x]] := Heap [Size];
Pos [Heap [Size]] := Pos [x];
Heap [Size] := 0;
Dec (Size);
p := Pos [x];
q := p DIV 2;
if (q > 0) and (Heap [q] < Heap [p]) then begin
while (q > 0) and (Heap [q] < Heap [p]) do begin
Exc (Pos [Heap [p]], Pos [Heap [q]]);
Exc (Heap [p], Heap [q]);
p := q;
q := p DIV 2;
end;
end
else begin
while ((Heap [p] < Heap [2 * p]) or (Heap [p] < Heap [2 * p + 1])) do
if (Heap [2 * p] > Heap [2 * p + 1]) then begin
Exc (Pos [Heap [p]], Pos [Heap [2 * p]]);
Exc (Heap [p], Heap [2 * p]);
p := 2 * p;
end
else begin
Exc (Pos [Heap [p]], Pos [Heap [2 * p + 1]]);
Exc (Heap [p], Heap [2 * p + 1]);
p := 2 * p + 1;
end;
end;
end;
procedure Solve;
var
i, k, j, v: LongInt;
begin
{Sortiram po X, i (dx [i], dx [i + 1]) x-koordinate trake}
pom := x;
Quick_Sort_X (1, 2 * n);
d := 0; i := 1;
while (i <= 2 * n) do begin
Inc (d);
dx [d] := pom [i];
while (dx [d] = pom [i]) and (i <= 2 * n) do Inc (i);
end;
{Sortiramo po Y i dy [i] = pozicija u ne soriranom nizu}
pom := y;
for i := 1 to 2 * n do dy [i] := i;
Quick_Sort_Y (1, 2 * n);
FillChar (Area, SizeOf (Area), 0);
for k := 1 to d - 1 do begin
FillChar (Heap, SizeOf (Heap), 0);
FillChar (Pos, SizeOf (Pos), 0);
j := 1;
while not ((x [dy [j]] <= dx [k]) and (dx [k + 1] <= x [dy [j] + n])) do Inc (j);
Heap [1] := dy [j];
Pos [dy [j]] := 1;
Size := 1;
for i := j + 1 to 2 * n do begin
Area [Color [Heap [1]]] := Area [Color [Heap [1]]] +
(dx [k + 1] - dx [k]) * (y [dy [i]] - y [dy [i - 1]]);
v := dy [i];
if (v > n) then v := v - n;
if (x [v] <= dx [k]) and (dx [k + 1] <= x [v + n]) then
if (dy [i] <= n) then
Insert (dy [i])
else
Delete (dy [i] - n);
end;
end;
end;
procedure Output;
var
i: LongInt;
begin
Assign (g, 'rect1.out');
ReWrite (g);
for i := 1 to MaxN do
if (Area [i] > 0) then
WriteLn (g, i, ' ', Area [i]);
Close (g);
end;
begin
InPut;
Solve;
OutPut;
end.
[ stf @ 05.07.2005. 08:11 ] @
''Izgurao'' sam nekako ovaj zadatak. Cassey, hvala ti puno!
Copyright (C) 2001-2025 by www.elitesecurity.org. All rights reserved.
|